基于奇異值分解的接收機自主完好性監測算法

陳 兵,楊志坤,賈 睿,韓依萌,李 軍,陳 丹,丁 可

(1.重慶九洲星熠導航設備有限公司,重慶 400037; 2.四川九洲技師學院,四川 綿陽 621000)

0 引言

完好性監測最初來源于民用航空用戶對航空系統高可靠性的需求。在飛機進離飛機場階段,飛機飛行的高度、所處的氣象條件及地理環境等因素都會導致飛行事故的發生,主要原因是缺乏完備可靠的完好性監測服務。

1987年R.M.Kalafus首次提出了接收機自主完好性監測(receiver autonomous integrity monitoring,RAIM)的概念(即一致性校驗冗余監測技術)并從理論上證明了故障檢測與故障識別所需的最少衛星數[1]。1986年Lee提出了偽距比較法(range comparison method)[2],通過比較冗余數據的預測觀測值與實際觀測值來進行故障檢測。同年Brown提出了基于卡爾曼濾波的RAIM算法[3]。1988年Parkinson提出了一種基于最小二乘的完好性監測方法即最小二乘殘差(least squares residual, LSR)法[4],通過對觀測點偽距觀測方程進行最小二乘估計,構造偽距殘差,根據偽距殘差統計量的卡方分布特性計算檢測統計量及門限,從而判斷衛星是否存在故障。同年,Sturza提出了奇偶空間矢量法(parity space vector method)[5],Sturza認為基于偽距殘差矢量的一致性檢測中,殘差矢量中的4個分量之間存在一定的關聯性,其關聯性會掩蓋信息中的不一致部分,而通過奇偶變換可以消除這種關聯。算法主要思路是對系數矩陣進行QR分解,使用奇偶矢量表示觀測量的粗差,從而可以簡單直觀地進行粗差的檢測與識別。文獻[6]證明了上述三種方法具有等價性,且只適用于單星故障監測,統稱為“快照”算法。Walter等人[7]提出了加權最小二乘RAIM算法,通過考慮觀測噪聲獲得的加權矩陣輔助最小二乘估計進行故障檢測。高文寧等人[8]利用慣導的輔助數據設計了一種基于多級Kalman濾波的北斗接收機完好性監測方案,給出了衛星導航接收機的RAIM濾波器結構與故障檢測和隔離方法,并對其可用性進行了推導。該方案可有效檢測并隔離單星階躍、慢速漂移、慢速隨機等北斗衛星偽距和偽距率故障,但算法復雜度高。楊傳森等人[9]考慮了偽距觀測模型線性化過程存在的截斷誤差和噪聲因素,提出了一種改進的總體最小二乘RAIM算法,使得殘差更精確、數據更可靠,具有一定的可用性。隋葉葉等人[10]在分析了最小二乘殘差法和奇偶矢量法的原理和方法的基礎上,提出了一種基于最小二乘法構造檢測統計量的奇偶矢量改進方法,從而提高了算法運行效率。王煜東等人[11]采用斜率加權,根據衛星特征斜率的大小構建加權矩陣,實驗結果表明基于斜率加權的最小二乘法的故障檢測率優于最小二乘法。

由于偽距定位精度的影響,基于偽距觀測量的完好性最高只適用于I類精密進近[12],本文研究基于偽距觀測量的完好性算法。隨著機載對精密進近的需求,特別是II/III類精密進近,很多學者開始研究基于載波相位觀測量的完好性算法[13]。胡杰等人[14]提出了一種雙頻地基增強系統(ground based augmen-tation system,GBAS)的無碼載偏離載波相位平滑偽距算法,解決了單頻單星座GBAS無法滿足飛機III類精密進近與著陸導航性能需求的問題,并且提升了系統的可用性。Li等人[15]提出使用雙差載波相位觀測量構造星歷故障檢驗統計量的方法,該方法同時考慮了星歷故障的影響和無幾何模糊度解算失敗的影響,從而抑制了星歷故障監測方法的虛警和漏檢誤差。實驗結果表明,該方法可以實現對A型和B型星歷故障[16]的實時監測。

上述文獻大多數是從偽距殘差矢量進行衛星故障的探測,但由于偽距殘差矢量中各分量具有一定的關聯性,掩飾了某些重要的不一致性信息。因此,本文提出了一種新的基于奇異值分解的接收機自主完好性監測(singular value decomposition to receiver autonomous integrity monitoring,SVD-RAIM)算法。基于奇異值空間矢量構造能夠直接反映故障衛星偏差信息的檢驗統計量,從而可以簡便地進行粗差的監測,更好地滿足完好性監測的需求。鑒于實際中完好性故障包含運控系統故障、導航系統故障、信號傳播異常以及地面接收處理故障等多類因素[17],仿真中以脈沖型和階躍型兩種故障方式進行SVD-RAIM算法對故障檢測與識別的驗證,結果表明,所提出的方法能夠正確檢測、識別故障,在特定參數下能夠達到很好的故障識別率。

1 算法理論與框架

SVD-RAIM算法整體框架如圖1所示,主要由構造檢驗統計量和衛星故障檢測識別兩個部分構成。

圖1 基于奇異值分解的接收機自主完好性監測算法Fig.1 Receiver autonomous integrity monitoring algorithm based on singular value decomposition

1.1 加權系數矩陣

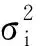
(1)

由于每顆衛星的觀測噪聲互不相關,那么第n顆衛星的噪聲協方差矩陣C可表示為

(2)

此時,W=C-1。

1.2 SVD-RAIM算法

根據衛星導航定位原理,偽距觀測方程可表示為

y=Hx+ε

(3)

其中,y為n×1維偽距觀測值的殘差矢量;n為可視衛星數;x為4×1維用戶狀態矢量,包括3個用戶接收機位置矢量修正數和1個接收機時鐘修正量;ε為n×1維觀測偽距噪聲矢量;在衛星導航定位解算模型中,系數觀測矩陣H是由各衛星到接收機視線軸的方向余弦矢量以及第4列全為1的常量組成。

對偽距觀測方程中的觀測系數矩陣H進行奇異值分解(SVD),即H=UDVT,可得

y=UDVTx+ε

(4)

其中,U為n×n維正交矩陣;D為n×4維對角奇異值矩陣;V為4×4維正交矩陣,表示觀測系數矩陣H的特征矢量。

對式(4)兩邊左乘UT,可得

UTy=DVTx+UTε

(5)

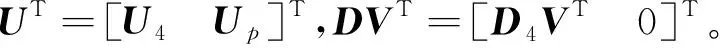
(6)

(7)

其中,Up定義為奇異值空間矩陣;奇異值空間矢量p為觀測偽距噪聲矢量在奇異值空間矩陣Up上的投影矢量,能夠直接反映故障衛星的偏差信息。

由式(7)可知,奇異值空間矢量p反映了故障衛星的偏差信息,即觀測信息誤差,本文基于奇異值空間矢量構造檢驗統計量,將奇異值空間矢量的數量積ppT作為檢驗統計量,進行衛星故障檢測。

式(7)中,觀測偽距誤差ε是通過奇異值空間矩陣Up的列向量反映到奇異值空間矢量上的,因此本文以ε和Up之間的幾何關系進行衛星的故障識別。

1.3 故障檢測

將奇異值空間矢量的數量積ppT作為檢驗統計量,那么加權奇異值空間矢量和WSSE可表示為pWpT,即

WSSE=pWpT

(8)

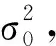
(9)

存在二元假設

(10)

在無衛星故障時,檢測結果應正常,若出現告警信息,則為誤警。給定誤警概率PFA,可確定門限值Td滿足

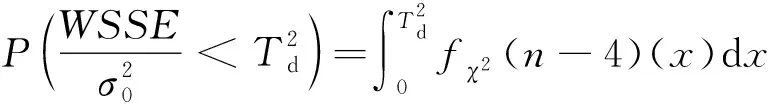
(11)

其中,fχ2(n-4)(x)表示自由度為n-4的卡方分布的概率密度函數。

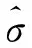
(12)

1.4 故障識別

檢測的目的是為了將檢測到的故障進行更好的識別和剔除。本文采用巴爾達數據粗差探測方法。該探測方法認為粗差衛星是特征偏差線與奇異值空間矢量p重合的衛星。本文為了最大化偏差的可見性,將p投影到Up的列矢量并進行歸一化,從而得到識別檢驗統計量

τi=|pTUp,i|/(σ0|Up,i|)

(13)

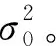
(14)

已知PFA,可計算得到Tτ。將每個檢測統計量與Tτ比較,若τi>Tτ,則表明該衛星有故障。

2 實驗結果與分析

為了驗證SVD-RAIM算法在衛星故障監測中的有效性,使用IGS數據中心提供的觀測站數據:brdc2000.06n、madr2000.06o和igs13843.sp3,總觀測歷元長度為2 850 s。圖2和圖3分別為觀測歷元內GPS衛星的可見性分布和可見衛星數。從圖3可知,該觀測歷元內衛星數都大于等于6顆,滿足接收機自主完好性故障檢測和識別條件。

圖2 不同歷元下的可見衛星分布Fig.2 The visible satellite distribution under different epochs

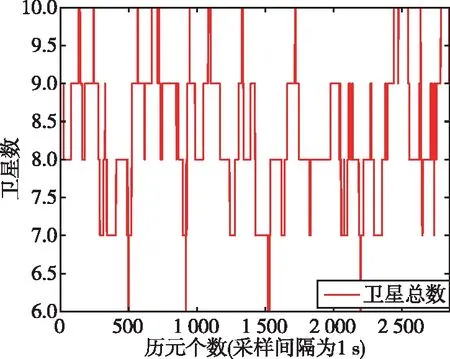
圖3 可見衛星個數Fig.3 The number of visible satellite

圖4所示為無故障情況下的檢驗統計量與檢測限值。由圖4可以看出,整個觀測歷元內檢測統計量總是低于檢測限值,即觀測過程不存在故障衛星。本文檢測限值由式(11)與式(12)獲得,其中,誤警概率PFA設置為1×10-5/h。

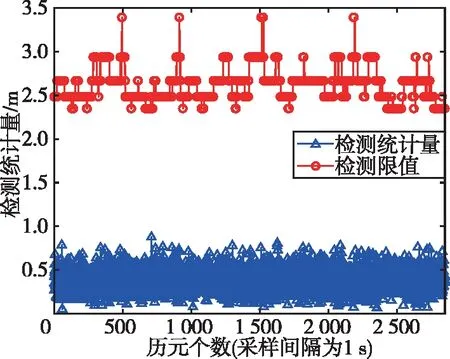
圖4 無故障情況下的檢驗統計量與檢測限值Fig.4 The test statistics and the test value under the non-fault condition

實際中,接收機觀測量數據異常多體現在有異常跳點或者一段時間內有較大誤差。因此,本文采用脈沖型和階躍型兩種故障模式進行SVD-RAIM算法仿真驗證。

2.1 脈沖型故障

本文以觀測歷元內的3號衛星為例,在第200個歷元處引入幅值為15σ0的脈沖故障,即在原偽距觀測量上增加幅值為15σ0的異常值,使用SVD-RAIM算法得到故障檢測和故障識別結果分別如圖5和圖6所示。其中,衛星可視狀態為當前歷元可觀測到用于參與定位的衛星數。

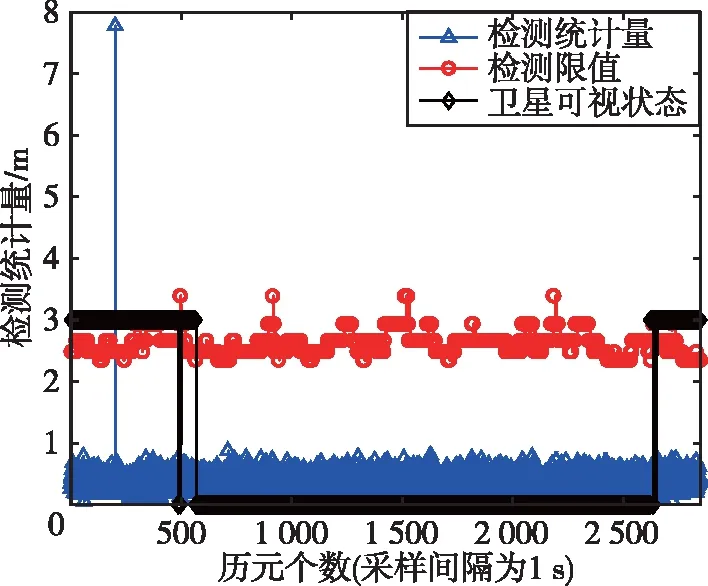
圖5 脈沖型故障:3號衛星故障檢測結果Fig.5 The pulse fault: fault detection results of satellite 3

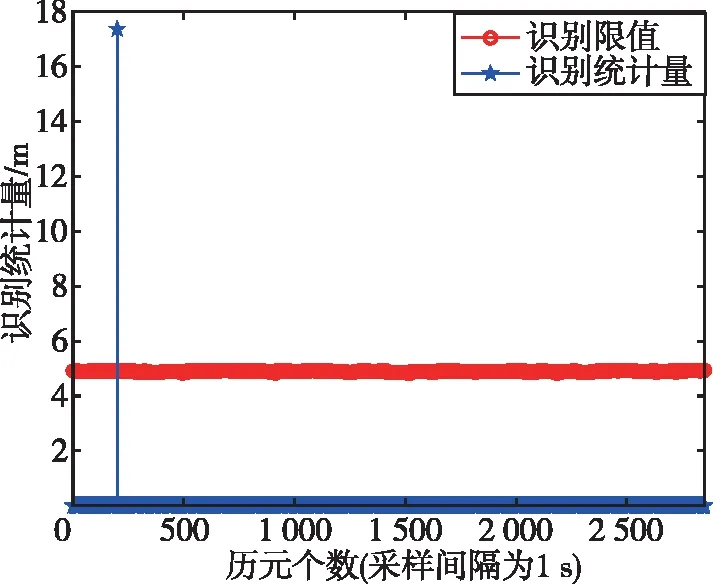
圖6 脈沖型故障:3號衛星故障識別結果Fig.6 The pulse fault: fault identification results of satellite 3

本文在第200個歷元處加入脈沖故障,由圖5可以看出,在第200個歷元處檢驗統計量超出檢測門限,即此時出現衛星故障,與本文設置故障歷元一致;圖6中相應的識別檢驗統計量也超出識別門限,即此時識別出了故障衛星。由此可以看出,本文所提算法對脈沖型故障具有很好的魯棒性。

2.2 階躍型故障

以3號衛星為例,在觀測的第200～450個歷元內加入幅值為15σ0的階躍故障,使用SVD-RAIM算法得到階躍故障檢測與識別結果分別如圖7和圖8所示。

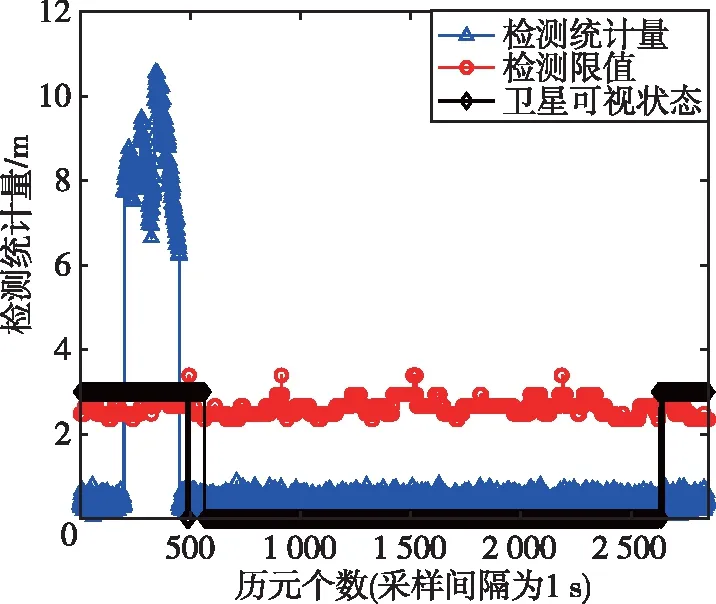
圖7 階躍型故障:3號衛星故障檢測結果Fig.7 The step fault: fault detection results of satellite 3

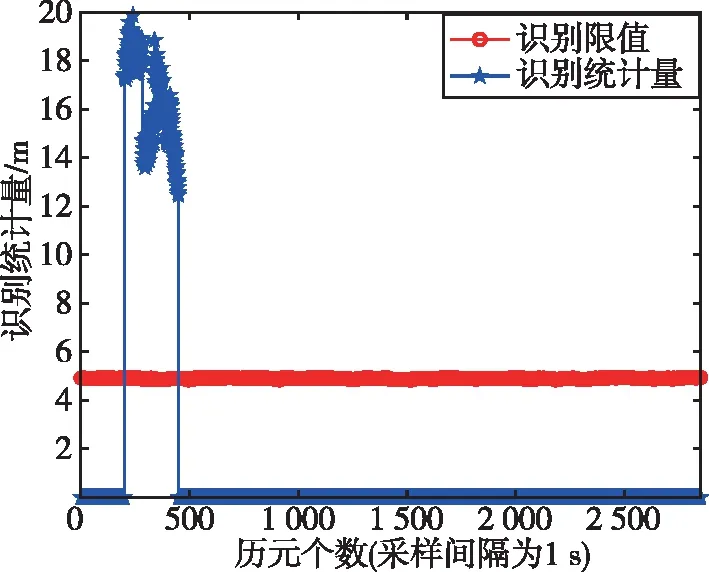
圖8 階躍型故障:3號衛星故障識別結果Fig.8 The step fault: fault identification results of satellite 3

如圖7所示,在第200～450個歷元處出現統計檢驗量超出檢測門限的情況,即在這段歷元內存在故障衛星;如圖8所示,識別統計量超出了識別門限,并成功識別出故障衛星。由此可得,本文所提算法對階躍型故障具有很好的魯棒性。

偽距誤差σ0也會對故障的檢測與識別產生影響。當可見星大于7顆時,分別引入15、20、25、30和35 m階躍故障(以3號衛星為例,在觀測的第200～450個歷元內加入相應誤差的階躍故障)時,偽距誤差σ0對故障識別的影響如表1所示。

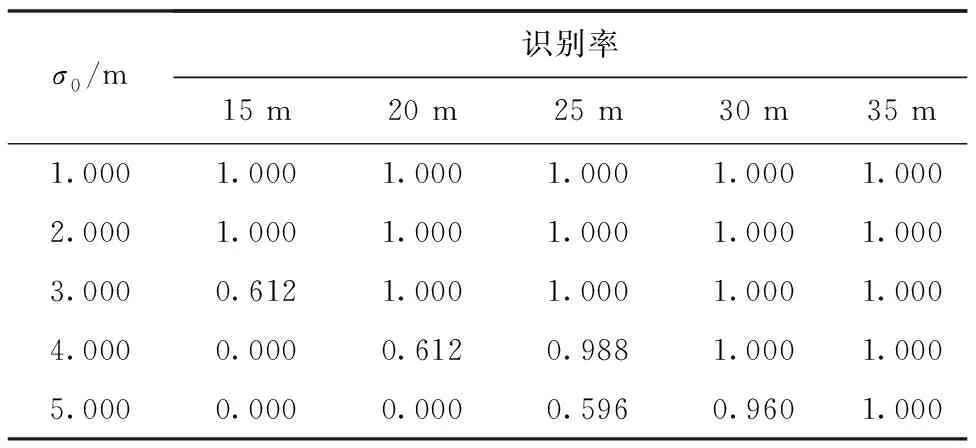
表1 σ0對故障識別的影響Table 1 The effect of σ0 on fault identification

從表1可以看出,當誤警概率PFA設置為1×10-5/h、σ0為3 m、引入階躍故障誤差為20 m時,算法能夠實現100%的故障識別率;當誤警概率PFA設置為1×10-5/h、σ0為4 m、引入階躍故障誤差為25 m時,算法能夠實現98.8%的故障識別率;當誤警概率PFA設置為1×10-5/h、σ0為5 m、引入階躍故障誤差為30 m時,算法能夠實現96%的故障識別率。其中,故障識別率為本方法檢測識別出的存在故障歷元個數與存在故障的歷元總數的比值。可以看出,本文算法在特定參數下能夠達到很好的故障識別率。

2.3 算法對比

與2.2節中相同的運行環境及參數設置情況下,針對傳統的基于奇偶矢量RAIM算法和本文所提方法進行了仿真對比。測試主要從算法故障監測性能方面進行了兩種方法的驗證對比,其中,監測引入故障采用階躍故障。實驗對比結果如圖9所示。

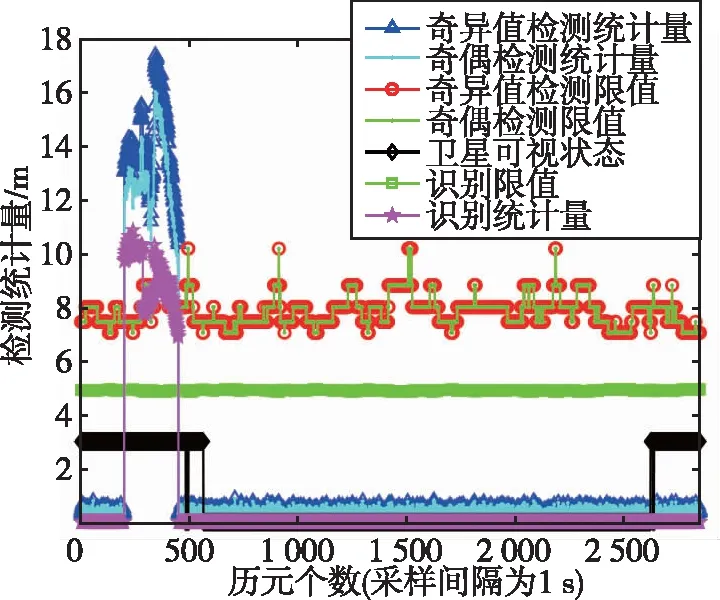
圖9 階躍型故障下兩種算法性能對比Fig.9 Performance comparision of two algorithm under step fault

圖9所示為階躍故障下,本文算法與奇偶矢量RAIM算法的性能對比。從比對結果可知,在故障檢測方面,相同故障檢測門限下,SVD-RAIM算法對故障異常檢測更敏感,對相同的故障偏差具有較大的檢測統計量,易于檢測。在故障識別上,兩種算法都能夠正確識別故障衛星。

3 結論

常見的完好性故障包含運控系統故障、導航系統故障、信號傳播異常以及地面接收處理故障等,本文基于奇異值分解的RAIM算法系統分析了脈沖型和階躍型兩種故障模式下衛星故障的檢測和識別。使用IGS數據中心提供的觀測站數據進行算法仿真驗證,結果表明,基于奇異值分解的RAIM算法計算量小且能夠正確檢測和識別故障衛星,算法在特定參數下能夠達到很好的故障識別率,滿足完好性監測需求。本文只研究了算法在單星故障情況下的故障檢測,未來將繼續研究本文算法在雙星、多星故障、漸變故障以及基于載波相位的精密進近方面的故障監測性能。