GNSS實時衛星鐘差估計在地震監測中的應用

王浩浩,郝 明,莊文泉

(中國地震局第二監測中心,西安 710054)

0 引言

近年來,隨著全球導航衛星系統(global navigation satellite system, GNSS)高頻定位技術的不斷發展,其在地殼運動監測領域發揮著越來越重要的作用,為地震監測提供了一種有效的新型技術途徑[1-2]。其中,利用差分相對定位技術可以計算得到監測站相對于某一固定參考站毫米級的動態位移,但監測區域內有時因地質條件等客觀因素難以布設觀測環境良好、穩定的基準站,而且坐標精確已知的基準站在強震發生階段可能會發生移動,導致動態解算的定位精度顯著降低[3-4]。而采用國際GNSS服務(international GNSS service, IGS)組織發布的精密衛星軌道和鐘差等產品的精密單點定位(precise point positioning, PPP)技術,具有不依賴于某一特定參考基準站、實時性強等優勢,僅利用單臺GNSS接收機即可獲得國際地球參考框架下高精度的“絕對位置”,具備準確捕捉地震位移波形的能力,更適合長距離、大范圍的地殼形變監測[3-4]。文獻[5]實驗結果表明,衛星鐘差的采樣率越高,利用PPP動態解捕捉遠場站點形變信息的優勢越明顯。文獻[6]利用武漢大學自主研發的PANDA軟件對高頻GNSS觀測信號進行PPP后處理,能夠很好地獲取2016-11-13新西蘭Mw7.8地震產生的動態位移特征。

地震瞬時地表動態位移的實時高可靠性監測對地震預警系統而言至關重要,能夠為震中以及震級的快速確定等研究工作提供關鍵信息[3]。然而,實時PPP高精度動態解的實現取決于精密衛星軌道和鐘差的實時估計性能。目前超快速實時預報軌道產品已經能夠滿足其時效性和可靠性等要求,但衛星鐘差的精確預報極易受到自身時頻特性以及復雜太空環境的影響,高可靠的厘米級GNSS實時衛星鐘差則需利用地面站觀測數據進行實時估計得到[7]。文獻[8]實時估計的多模GNSS衛星鐘差與武漢大學最終精密鐘差互差優于0.2 ns。文獻[9-10]利用均方根信息濾波實現GNSS四系統實時衛星鐘差的快速估計,且與最終精密鐘差產品符合性較好。文獻[11]提出了一種基于序貫最小二乘的在線質量控制方法,GNSS四系統實時估計衛星鐘差的標準差均值優于0.1 ns。

鑒于此,本文以長安大學北斗分析中心為平臺,基于多模全球導航衛星系統實驗跟蹤網(multi-GNSS experiment, MGEX)監測站1 Hz的GNSS觀測數據,采用模型嚴密、精度較高的非差估計法[12],實現了多模GNSS衛星鐘差的實時估計和性能評估,并將其用于高頻動態PPP實時獲取2021年漾濞Mw6.4地震和瑪多Mw7.4地震發生時段的地表形變波形,具體分析震時點位的運動變化情況。

1 數據處理

1.1 鐘差估計

本文采用無電離層組合觀測值進行GNSS衛星鐘差的實時估計,非差偽距和載波相位的觀測方程為

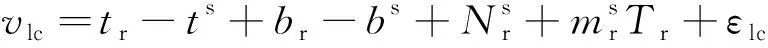
(1)

由于公式中的偏差參數具有很強甚至完全的線性相關性,將其作為未知數進行估計,不僅會引入大量待估參數,還會減弱衛星鐘差的估計精度。其中,衛星端的碼偏差參數具有較高的時間穩定性,可以在觀測方程中將其合并到衛星的鐘誤差參數中,而且相位延遲偏差可以被相應的相位模糊度參數吸收。進而可得觀測模型

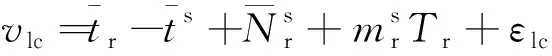
(2)

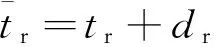
對于全球定位系統(global positioning system, GPS)、格洛納斯衛星導航系統(global navigation satellite system, GLONASS)、伽利略衛星導航系統(Galileo satellite navigation system, Galileo)以及我國的北斗衛星導航系統(BeiDou navigation satellite system, BDS)而言,不同衛星導航系統所采用的時空基準以及信號體制不一致,導致衛星信號在GNSS接收機內部產生系統間偏差(inter system bias, ISB)以及GLONASS所特有的頻率間偏差(inter frequency bias, IFB)[11]。若以GPS時間系統為基準,則顧及ISB/IFB參數的GNSS衛星鐘差實時估計模型為

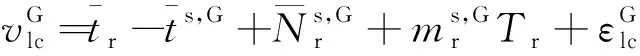
(3)

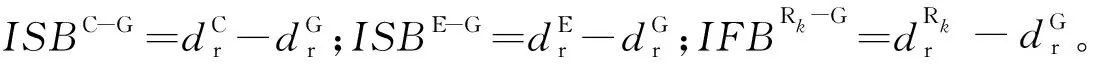
1.2 處理策略

無電離層組合模型是GNSS精密衛星鐘差估計、精密單點定位等數據處理常用的函數模型,表1總結了GNSS衛星鐘差實時估計以及實時動態PPP基于該模型的數據處理策略。對于GNSS衛星鐘差的實時估計,則是在觀測方程中將衛星鐘誤差作為白噪聲進行估計以免受到鐘跳的影響,將衛星軌道和測站坐標作為已知值進行改正。對于GNSS實時動態PPP,則是將測站的位置坐標作為待估參數進行估計,將精密衛星軌道和衛星鐘差作為已知值進行改正。

表1 數據處理策略Tab.1 Data processing strategy

2 多模GNSS實時衛星鐘差估計分析

在MGEX中選取60個均勻分布在全球的連續運行跟蹤站。從IGS下載2021年5月19日—2021年5月22日連續4 d所選測站1 s采樣間隔的GNSS觀測數據用于衛星鐘差的實時估計。在實時估計多模GNSS衛星鐘差的過程中,測站始終處于靜止狀態且位置已知,可以將測站坐標固定到IGS周解。現階段,超快速實時預報軌道產品與最終精密軌道產品的精度量級相當,衛星軌道可以固定為武漢大學提供的包含G/R/E/C四系統軌道的6 h超快速解,以減少待估參數的個數。同時,選擇某一測站的接收機鐘差作為參考基準鐘進行約束[15],基于雙頻非差消電離層組合的載波相位和偽距觀測值,采用序貫最小二乘平差和驗后殘差質量控制算法,最終估計得到歷元間隔為5 s的多模GNSS實時衛星鐘差。

2.1 估計時間分析

當利用60個測站構成的地面跟蹤站網進行多模GNSS衛星鐘差實時估計時,每個歷元大約需要處理3 000個觀測值并對將近2 000維的矩陣進行求逆。每個歷元需要處理的觀測值數目和法方程維數如圖1所示。為加快高維矩陣的運算速度,提高鐘差估計算法的計算效率,本文采用LAPACK函數庫中相關的矩陣運算解算法方程,以實現多模GNSS實時衛星鐘差的快速估計[16]。圖2統計了LAPACK方法下,實時估計2021年年積日第141天G/R/E/C四系統衛星鐘差時每個歷元的計算時間。可以得出,在全球分布60個連續運行跟蹤站的情況下,所有歷元的鐘差估計耗時均小于5 s,單歷元鐘差估計的平均計算時間為3.4 s,可見上述算法對高頻觀測數據的處理效率足以實時估計5 s歷元間隔的多模GNSS衛星鐘差。

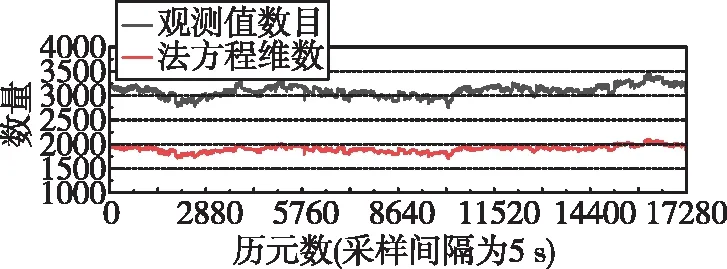
圖1 每個歷元的觀測值數目和法方程維數Fig.1 The number of observations and the dimension of the normal equation system at each epoch

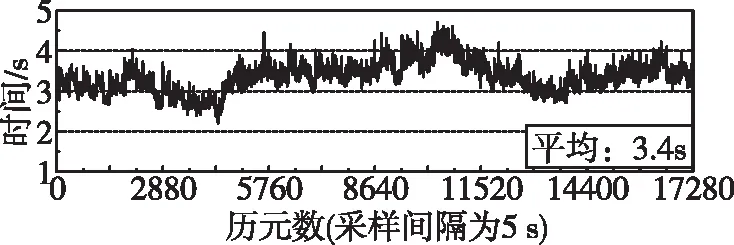
圖2 多模GNSS實時鐘差單歷元估計時間Fig.2 The computation time for the multi-GNSS real-time clock offset estimation at each epoch

2.2 鐘差精度分析

采用二次差的方法計算實時估計衛星鐘差與武漢大學最終精密衛星鐘差的差異[17],利用該差異統計其標準差(standard deviation, STD),并與法國空間研究中心(Centre National D’études Spatiales,CNES)實時播發的衛星鐘差產品進行對比,對多模GNSS實時衛星鐘差估計算法的有效性進行評估。考慮到衛星鐘差實時估計的收斂時間,僅對2021年5月20日—2021年5月22日(年積日第140—142天)的實時衛星鐘差進行精度分析,并在圖3中展示了單顆衛星連續3 d的鐘誤差時間序列,BDS衛星鐘差的整體穩定性要弱于其他導航衛星系統。同時,GNSS實時估計鐘差與CNES實時鐘差產品的精度對比如表2和圖4所示。其中,表2為GPS、GLONASS、Galileo、BDS各系統單天的平均STD對比,圖4為GNSS每顆衛星連續3 d的平均STD對比。

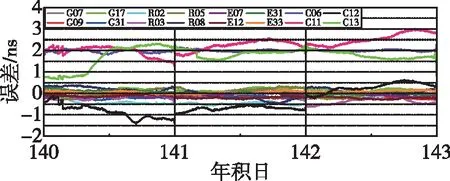
圖3 GPS/GLONASS/Galileo/BDS衛星鐘誤差的時間序列Fig.3 Time series of GPS/GLONASS/Galileo/BDS satellite clock error

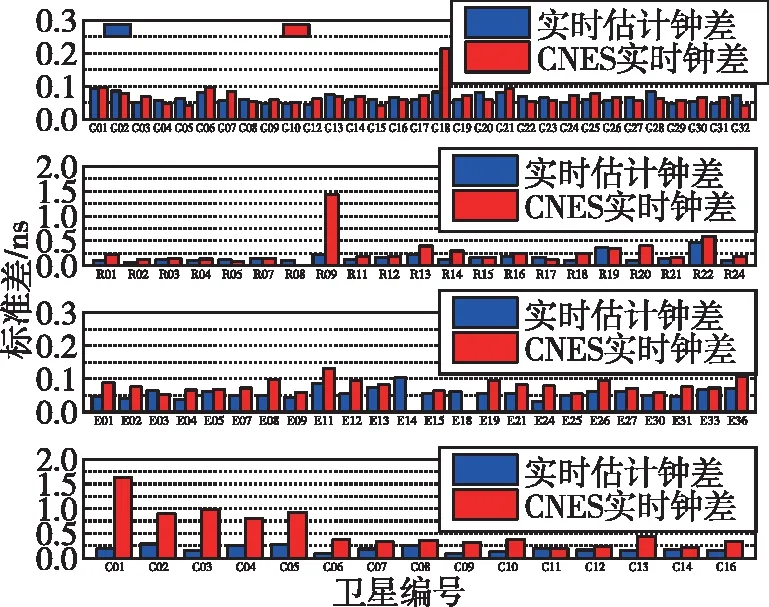
圖4 GPS/GLONASS/Galileo/BDS衛星鐘差精度對比Fig.4 Accuracy comparison of GPS/GLONASS/Galileo/BDS satellite clock

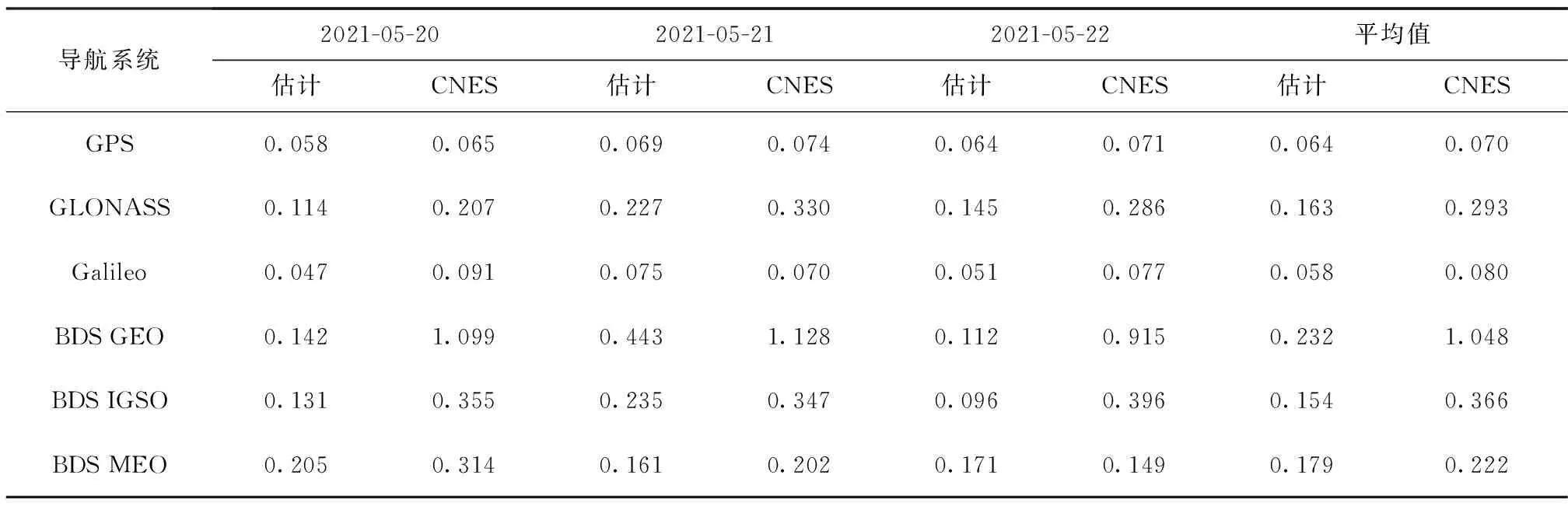
表2 衛星鐘差精度統計Tab.2 Accuracy statistics of satellites clock offset ns

由于衛星鐘差與軌道誤差的耦合性,在實時估計多模GNSS衛星鐘差時,90%的軌道徑向誤差會被鐘差所吸收,從而導致實時估計鐘差和最終精密鐘差兩者之間并不完全吻合[18]。結合表2和圖4可以得出,實時估計GPS衛星鐘差的STD數值區間為0.044～0.094 ns,每顆GPS衛星的鐘差精度均優于0.1 ns,整體穩定性較好,所有衛星的STD均值為0.064 ns。除G18衛星的鐘差STD值為0.215 ns外,CNES實時播發的GPS衛星鐘差產品與自主估計的GPS實時鐘差精度基本一致,這可能與G18衛星的型號為Block Ⅲ,發射時間較晚,CNES的軌道模型還未對其完全精化有關。對于Galileo系統而言,實時估計衛星鐘差與CNES實時衛星鐘差二次差結果序列相差不大,所有Galileo衛星的STD均值分別為0.058 ns和0.080 ns,且每顆衛星的鐘差精度基本上均能優于0.1 ns,能夠達到與GPS衛星鐘差相當的精度水平,這可能與Galileo衛星所搭載的高精度氫原子鐘有關。CNES實時播發的GLONASS鐘差產品中,R09衛星連續3 d的鐘差精度均將達到1.5 ns,這是因為該衛星的鐘差序列出現多次中斷,導致精度異常。對于其他GLONASS衛星,二次差結果序列的STD數值區間為0.087～0.598 ns,STD均值為0.232 ns,稍差于自主估計的GLONASS實時衛星鐘差精度,所有衛星的STD均值為0.163 ns。對于CNES實時BDS衛星鐘差產品,地球靜止軌道(geostationary Earth orbit,GEO)衛星的鐘差精度明顯差于中圓地球軌道(medium Earth orbit,MEO)衛星和傾斜地球同步軌道(inclined geosynchronous orbit,IGSO)衛星,導致BDS衛星鐘差整體精度較差。除GEO衛星外,其余MEO/IGSO衛星的STD均值為0.294 ns,大約是自主估計BDS MEO/IGSO實時衛星鐘差STD均值的2倍。從整體上看,自主估計的GPS、GLONASS、Galileo、BDS GEO、BDS IGSO和BDS MEO實時衛星鐘差STD均值分別為0.064、0.163、0.058、0.232、0.154和0.179 ns,要稍優于CNES實時播發的衛星鐘差產品,兩者G/R/E/C四系統的STD均值分別為0.142 ns和0.347 ns,這是由于在實時估計GNSS衛星鐘差時,二者選取測站的數據質量和解算策略存在差異所致。

3 震時地表形變分析

3.1 2021年云南漾濞Mw 6.4地震

為進一步評估實時估計多模GNSS衛星鐘差的精度和穩定性,利用中國大陸構造環境監測網絡(簡稱“陸態網絡”)基準站2021年5月21日21:45—21:59時段內的高頻GNSS觀測數據,基準站分布情況如圖5所示,采用表1中實時動態PPP的數據處理策略,基于5 s歷元間隔的GNSS實時衛星鐘差,在實時處理的定位模式下,通過序貫最小二乘估計方法,歷元之間不繼承坐標信息,分別進行GPS單系統、GNSS多系統的高頻動態PPP,并與武漢大學最終精密衛星鐘差的GNSS多系統組合動態PPP結果進行對比(表3),從而得到不同實驗下2021年云南漾濞Mw6.4地震發震時段內單歷元高頻動態解的時間序列。上述3種高頻動態PPP實驗分別對應實驗1、實驗2和實驗3,在不同定位實驗下,云南下關站(XIAG)、云南云龍站(YNYL)和云南麗江站(YNLJ)在東(East,E)、北(North,N)和高程(Up,U)方向上的動態位移時間序列如圖6所示,圖中垂直于橫軸的紅色實線為漾濞地震的發震時刻。

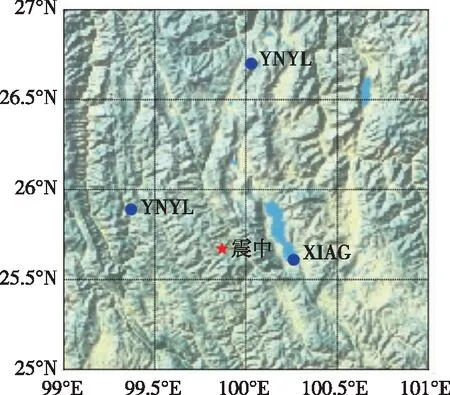
圖5 漾濞地震震中周邊GNSS基準站分布Fig.5 Distribution of GNSS reference station around the epicenter of Yangbi earthquake

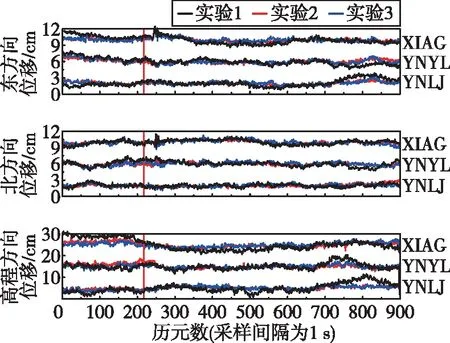
圖6 漾濞地震發生時段的動態位移時間序列Fig.6 The time series of dynamic displacement during the Yangbi earthquake

表3 不同測站高頻動態PPP的標準差Tab.3 Standard deviation of high-rate kinematic PPP at different stations

由圖6和表3可見,隨著其他系統的加入,基于實時估計衛星鐘差的GNSS多系統融合精密單點定位的動態位移波形更為穩定,其高頻動態解在E、N、U方向上的平均標準差分別為0.4、0.3、1.0 cm,相對于GPS單系統動態定位結果的平均標準差,在三個方向上分別提升了33%、25%和50%,印證了多系統融合定位的優越性[19]。同時,自主估計的GNSS實時衛星鐘差與武漢大學最終精密衛星鐘差的定位性能相當,其GNSS多系統組合PPP動態解的平均標準差能夠達到水平方向0.5 cm左右,垂直方向1.0 cm左右的精度水平。對于2021年5月21日云南漾濞地震,GNSS高頻動態解可以觀測到距震中39.7 km的XIAG站在水平方向上具有相對明顯的波動,這與文獻[20]漾濞地震的水平位移主要發生在震中距50 km范圍內相吻合。可見,基于上述數學模型估計的多模GNSS衛星鐘差能夠用于實時監測地震發生階段地表的動態形變特征。

3.2 2021年青海瑪多Mw 7.4地震

據中國地震臺網正式測定:北京時間2021年5月22日2時4分,青海省果洛藏族自治州瑪多縣(震中34.59°N,98.34°E)發生7.4級地震,震源深度17 km[21]。此次地震是中國大陸地區內繼2008年汶川Mw8.0地震后發生的震級最大的地震,其劇烈的地殼形變信號能夠被區域內連續運行的GNSS基準站可靠監測[22]。為具體分析瑪多Mw7.4地震發生階段對周圍地表形變的影響,利用中國地震臺網中心提供的震源周邊地區10個陸態網絡基準站的高頻GNSS觀測數據,這10個基準站分別為青海瑪多站(QHMD)、青海瑪沁站(QHMQ)、青海都蘭站(QHDL)、青海班瑪站(QHBM)、青海德令哈站(DLHA)、甘肅瑪曲站(GSMA)、四川甘孜站(SCGZ)、青海格爾木站(QHGE)、青海西寧站(XNIN)和西藏昌都站(XZCD),基準站分布情況如圖7所示。以地震發生前3 d的精密坐標的平均值為參考值,基于自主估計的2021年年積日第141天實時衛星鐘差進行GNSS多系統組合實時動態PPP,獲取瑪多地震震后5 min時段內不同基準站高頻動態解在E、N、U方向上隨時間變化的位移序列,如圖8所示。同時,對上述10個基準站震前3 d以及震后1 d的低頻GNSS觀測數據進行事后靜態PPP處理得到精密坐標的單天解,然后分別計算3個坐標分量上地震前后基準站位置的坐標平均值,通過差分獲得瑪多地震高可靠性的同震形變[23],并與GNSS多系統組合實時動態PPP獲得的同震形變進行對比,具體形變結果如表4所示。

圖7 瑪多地震震中周邊GNSS基準站分布Fig.7 Distribution of GNSS reference stations around the epicenter of Madoi earthquake

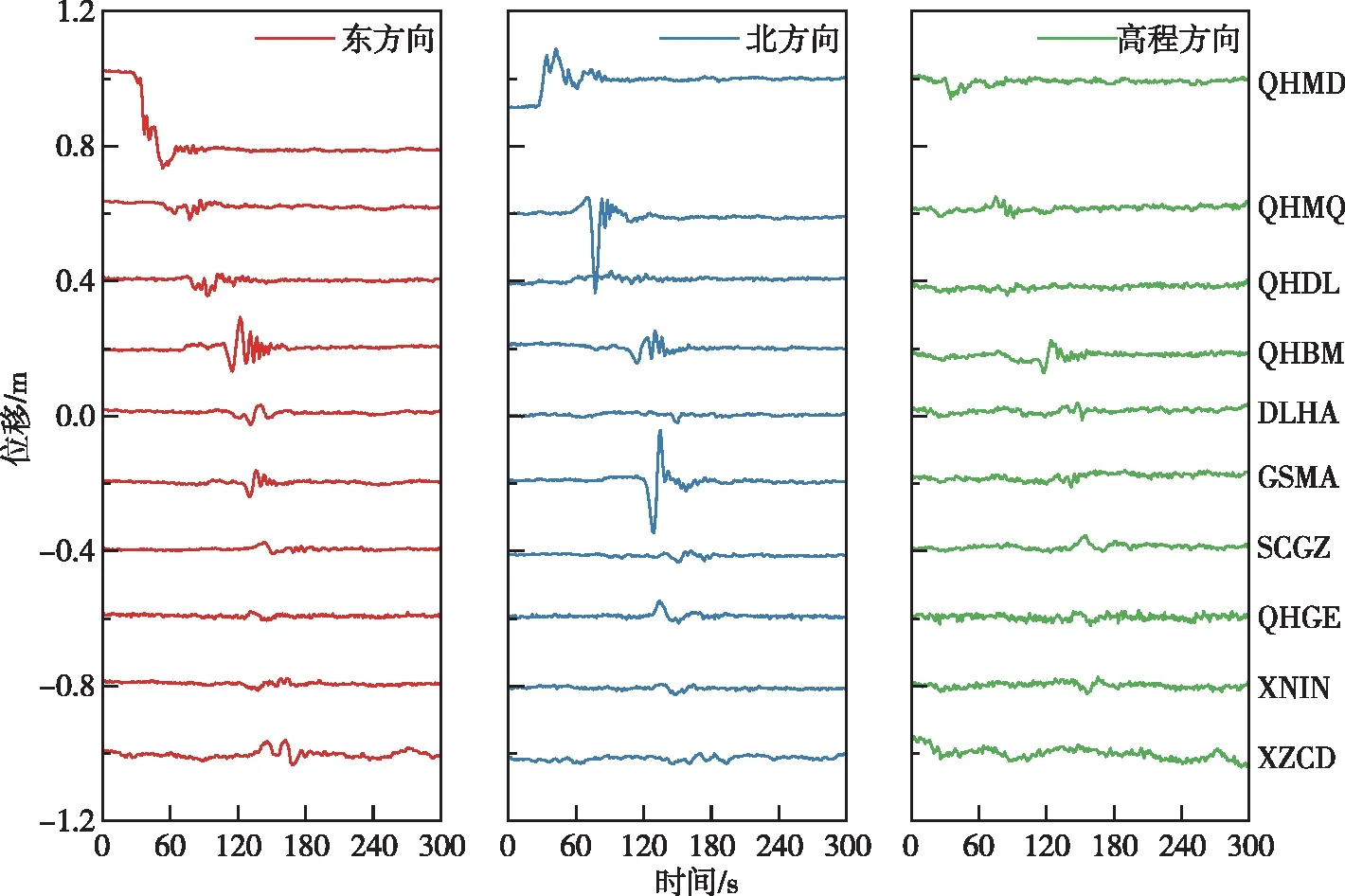
圖8 不同測站動態位移時間序列Fig.8 The time series of dynamic displacement at different stations

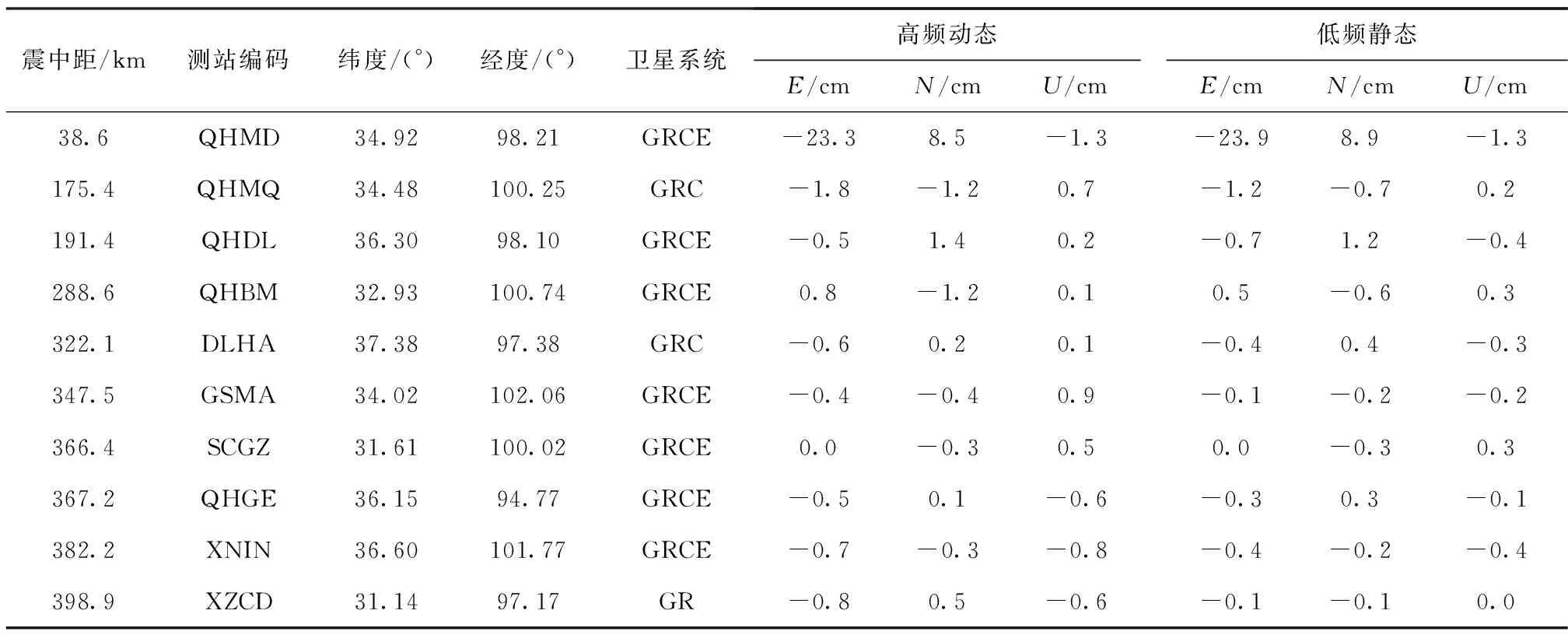
表4 基于高頻和低頻GNSS觀測的地表形變Tab.4 The surface deformation from 1 s and 30 s sampling GNSS observation data

由圖8可見,當瑪多地震發生后,10個陸態網絡基準站在不同時刻均發生不同程度的波動,且開始波動時刻隨基準站震中距的增大而延遲,影響區域可達距震中約400 km。其中,距震中約39 km的陸態網絡GNSS基準站QHMD最先感知到地震波,受瑪多地震的影響也最大,其位置在東西向和南北向均發生不可逆的永久性位移,東西向為23.3 cm,南北向為8.5 cm。不同于東西方向上的動態位移特征,QHMQ和GSMA相對于其他基準站在南北向受到瑪多地震的影響最為顯著,其震時最大動態位移分別約為23.5 cm和15.6 cm,說明地震對震源周圍站點的影響不僅和震中距有關,與其方位角也有一定的相關性[24]。然而,瑪多地震在垂直方向上對震源周邊基準站的影響相對較弱,10個基準站均未出現顯著的位移形變。從表4可以得出,受益于GNSS多系統融合具有更為穩健的定位精度,其實時PPP高頻動態解能夠有效地獲取地震發生階段各測站在水平方向上較為準確的地表形變量,與低頻GNSS觀測的形變結果基本一致,而兩者在垂直方向上的差值最大為1.1 cm,可靠性相對較差。綜上所述,基于多模GNSS實時衛星鐘差的PPP高頻動態解可以有效地揭示瑪多地震的震時地表形變特征。

4 結論

本文采用MGEX中60個連續跟蹤站的1 Hz觀測數據,基于序貫最小二乘算法,實現了多模GNSS衛星鐘差的實時估計,并將其用于GNSS多系統組合的高頻動態PPP,具體分析了2021年云南漾濞Mw6.4地震和瑪多Mw7.4地震的震時地表形變特征,得到以下結論:

1)自主估計的GPS、GLONASS、Galileo、BDS GEO、BDS IGSO和BDS MEO實時衛星鐘差STD均值分別為0.064、0.163、0.058、0.232、0.154和0.179 ns,整體上稍優于CNES實時播發的衛星鐘差產品。

2)基于實時估計衛星鐘差的GNSS多系統組合動態PPP在E、N、U三個方向上的平均標準差分別為0.4、0.3、1.0 cm,相對于GPS單系統的定位結果分別提升了33%、25%和50%,能夠提供波形更為穩定的動態位移時間序列。

3)GNSS多系統融合的實時PPP高頻動態解能夠快速有效地獲取地震發生階段站點的形變特征,為斷層運動特征的初步判定以及地震矩震級的快速確定提供較高可靠性的信息。