航空發動機起動機送修決策方法

夏存江，韓篤銘

（中國民用航空飛行學院航空工程學院，四川廣漢 618307）

0 引言

飛機發動機持續適航性關系到民航飛機運行安全和運營成本[1]。依據中國民航規章《大型飛機公共運輸承運人運行合格審定規則》，合格證持有人應當為其所運營的每架飛機的發動機編制維修方案[2]，以保證發動機的持續適航性。維修方案主要依靠維護手冊編制[3]，是飛機維護工作的基本文件[4-5]。維修手冊中對屬于“安全影響”類的部件具有明確的維修間隔標準，但缺乏關于“非安全影響類”部件軟時限的詳細描述。部件的軟時限與硬時限不同，是非強制性的。相關維修計劃指導文件建議部件的累積工作時間達到軟時限附近時擇機拆下部件送修[6]。空氣渦輪起動機（Air Turbine Starter，ATS）是發動機的重要性能部件[7]。作為航空發動機的附件，ATS 的功用是當飛機在地面時接通地面氣源為發動機提供起動動力[8]。雖然起動機只在飛機處于地面狀態時工作，不會對飛行安全產生直接影響，但其可靠性一直處于低水平會直接影響部件拆修頻率和航班延誤率，使得航空公司承受巨大的維修成本和飛機延誤成本[9]。因此制定合理的ATS 送修及維護時限不僅能夠確保發動機運行的安全性，還能降低維修成本、提高經濟效益[10-11]。

目前國內對于空氣渦輪起動機的送修決策研究頗少。蔣陵平[12]等使用威布爾分布計算通航飛機起動機的平均壽命，及劉正華[8]用基于經驗模態分解和相關向量機的方法預測的起動器剩余使用壽命，能夠為起動機送修決策提供一定參考，但都缺乏維護成本的考慮。民航領域關于維修間隔的研究多針對飛機或發動機的重要安全性部件，劉濤等[13]針對符合3 參數威布爾分布的飛機系統部件，依據其壽命分布來確定維修間隔，并用實例驗證了方法；盧翔等[14]在可靠性統計模型的基礎上建立了基于可用度和費用率模型的多目標維修間隔決策模型，針對維修成本優化了部件的維修間隔。上述2 種維修間隔制定方法都是基于可靠性統計模型所建立的，在選擇模型分布時缺乏對模型的有效性檢驗。袁忠大等[15]提出了一種相關向量機與經驗模型融合分解的起動機剩余壽命預測方法，該方法一定程度提高了對起動機剩余壽命預測的精度，但是并沒有給出具體的起動機軟時限制定方案。相關統計數據表明，某航空公司17架737機隊每年平均4次起動機故障中，有2起會導致航班延誤，平均每次延誤成本達到19.7 萬元。航空公司使用的飛機維修手冊并沒有提供空氣渦輪起動機的維護及送修間隔信息。綜上所述，在民機空氣渦輪起動機維護領域迫切需要一種完善的送修和維護決策方法，來降低起動機故障成本，完善航空公司運營秩序。

本文基于起動機使用數據研究了起動機軟時限制定模型、期望損失模型和經濟最優條件下的起動機維護檢查間隔。以液壓機械組件（HMU）為案例，討論了軟時限制定模型的廣泛應用價值。

1 故障分布

發動機的零部件復雜多樣，不同零部件的故障數據分布類型也不同。在查閱諸多信息和文獻之后，總結了在實際發動機可靠性分析場景中常用的分布類型及各自適用特點。

1.1 指數分布

指數分布的特點是當失效率恒定時會產生無記憶屬性，即1 個使用過的部件壽命與當前老化時間無關。因此用指數分布進行可靠性分析時，要求分析對象的失效率是穩定的，部件沒有早期故障和耗損故障階段。在航空維修領域，指數分布多被用于電子設備的可靠性分析中。

概率密度函數為

式中：λ為分布參數；t為時間。

可靠度函數為

1.2 正態分布

正態分布的特點為失效率會隨時間逐漸增加。正態分布多用于描述由于磨損而發生故障的部件，對于航空發動機的一些機械組件具有較好擬合能力。

概率密度函數為

式中：u為均值；σ為標準差。

1.3 威布爾分布

威布爾分布適用范圍廣泛，適用于分析偶然故障、早期故障、耗損故障等不同類型的壽命數據，對各種類型的數據均具有較強的擬合能力。同時威布爾分布也是最多被用于航空器部件結構可靠性分析的模型。

概率密度函數為

式中：β為形狀參數；η為尺度參數；g為位置參數。

失效分布函數為

可靠度函數為

2 分布模型選擇策略

選擇統計分布模型時，有4 種方法：（1）基于對系統運行原理及物理特性的了解；（2）基于經驗選擇統計模型；（3）嘗試-誤差法；（4）圖形方法。威布爾分布具有較強的適用性，已廣泛應用于航空發動機可靠性評估中[15]；正態分布針對機械組件具有較好的擬合能力，指數分布則多用于電子設備的可靠性分析。在航空領域種3 種分布均是常用模型，因此在選擇分布模型時，結合方法2、3總結出以下策略：

（1）首先考慮威布爾分布模型。使用K-S檢驗方法對其做有效性檢驗。如果威布爾模型通過檢驗，則選擇威布爾分布模型進行維修間隔建模。如果全部通過檢驗，則選擇檢驗水平最小的；

（2）如果威布爾分布不能通過檢驗，則按此方法逐一考慮正態分布和指數分布。

3 分布模型參數估計

本文選取常用的極大似然估計法進行分布模型參數估計。極大似然估計是最常用的經典統計方法，基本思路是：由樣本值選擇參數，求得使樣本發生的概率最大時方程的解，即為參數估計值。

假設針對某類機械部件收集到了n次的故障數據，其中包括部件壽命數據TSN（Time Since New）（單位：飛行小時）。產品的n次壽命數為t1≤t2≤…≤tn，樣本{ti}來自總體T的樣本。把樣本{ti}(i=1,2,…,n)代入概率密度函數，對其取對數求和得似然函數為

關于β和η對似然函數求偏導，得到似然方程為

使偏導數為零，上式可變為

用迭代算法求解上述方程，即可求得形狀參數和尺度參數的估計值β?、η?。

4 有效性檢驗

在以故障分布模型為基礎進行可靠性分析時，首先要對模型進行有效性檢驗。柯爾莫哥洛夫（K-S）方法檢驗的是經驗分布函數與所擬合理論分布函數之間的差異性是否顯著，它既適用于大樣本試驗，又適用于小樣本試驗情況[16]。在實際的發動機維護場景中，發動機零部件復雜多樣，針對不同部件提取到的樣本數據量也不統一，為此在做有效性檢驗時首選柯爾莫哥洛夫方法。具體步驟如下：

（1）給出統計假設檢驗

式中：F0(x)為已知的連續分布函數；F(x)為經驗分布函數。

（2）針對樣本{ti}，寫出經驗分布函數

（3）檢驗統計量Dn的計算方法為

（4）K-S的檢驗規則為：當Dn>Dn,a時，拒絕H0，否則接受H0。其中a為顯著性水平，文中取0.05，Dn,a為統計量Dn的精確分布分位點，可查K-S臨界值表得到。

5 決策方法

對于發動機中屬于非安全影響類的部件不會嚴格限制部件的可靠度。但是考慮到過低的可靠性水平會極大影響部件的可用度，因此針對此類部件本文提出了一種新的送修決策方法。即把部件平均可靠度1 階導數的極值點對應的維修間隔作為軟時限，使得部件可靠度在快速下降時能夠得到及時送修維護。

假設部件的周期為T，平均預防性檢查時間為Tp，平均可用時間為T-Tp。則周期內平均可靠度為

最終利用插值法可以計算出平均可靠度1 階導數的極值點，進而得到最終的部件送修軟時限。

此外，某些特殊非安全影響類部件發生損壞會造成嚴重的經濟損失，本文針對此類部件綜合考慮維修成本和延誤成本因素，建立了檢查間隔模型。

假設部件檢查的間隔為T，部件檢查及維護1 次的成本為b，維修成本為c，由于部件臨時故障所造成的平均延誤成本為d，檢查及維護所減少的故障發生率為a。則部件檢查的單位時間成本P1=b/T，期望換修成本，期望延誤成本d，則總期望損失為

函數P的極小值點對應的檢查間隔T即是最優檢查間隔。

6 案例分析

6.1 案例1

以某航空公司波音737 飛機空氣渦輪起動機為例進行案例分析。整個機隊的起動機歷史故障數據（數據來源于某航空公司維修記錄表）見表1。

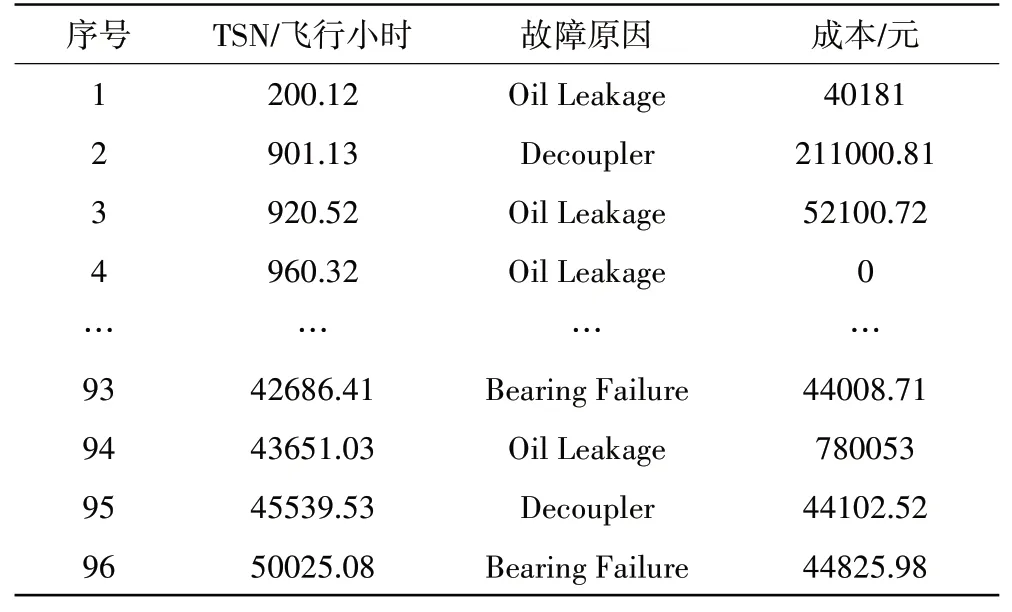
表1 起動機歷史故障數據

以整個機隊的空氣渦輪起動機的TSN（Time Since New）數據為樣本，將其按由小到大順序進行排列，得到有序樣本{ti|i=1,2,…,96}，按前文模型選擇策略，首先計算威布爾分布參數。將樣本數據代入式（9）計算得到威布爾分布的形狀參數β?=1.5611，尺度參數可寫出威布爾分布函數為

將樣本{ti}代入式（12）后計算得到D96=0.1420。查K-S臨界值表得到D96.0.05=0.1388。這里D96>D96.0.05，所以H0假設不成立。

依據模型選擇策略，放棄威布爾分布，進一步驗證正態分布。按前述方法，計算得到正態分布的參數估計值標準差檢驗水平D96=0.0777 。由于D96>D96.0.05，不拒絕H0假設。即顯著性水平取0.05時，正態分布通過了K-S檢驗。

正態分布概率密度函數為

累積分布函數為

可靠度函數為

此外為了驗證K-S檢驗在所提出的“分布模型選擇策略”下的有效性，求解出3 種分布函數的參數估計值及其檢驗水平，結果見表2。

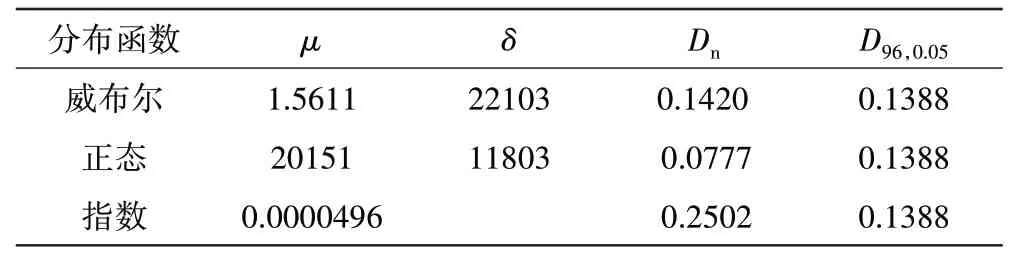
表2 參數估計值及檢驗水平

繪制出樣本點、正態分布、威布爾分布和指數分布的累積概率分布，起動機累積概率分布如圖1所示。

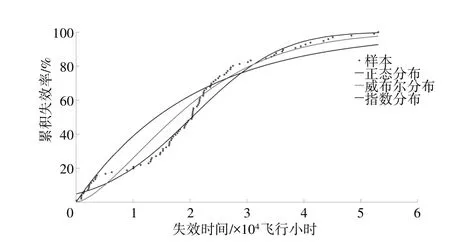
圖1 起動機累積概率分布

從表2 中可見，當顯著性水平a=0.05 時，只有正態分布的Dn>D96.0.05，通過K-S檢驗。而圖1 中顯示的正態分布對于樣本點的擬合效果要優于威布爾和指數分布。側面說明K-S檢驗在“分布模型選擇策略”下的可用性。因此，對于此樣本數據將選擇正態分布模型進行送修軟時限建模。

將式（18）中R(t)代入式（13）得到平均可靠度為

其中Tp以10 飛行小時、平均可靠度以90%為例進行計算，得到維修間隔T為9170 飛行小時。進而以1%為步長，依次求得平均可靠度為10%~90%對應的維修間隔及斜率。平均可靠度及斜率如圖2所示。

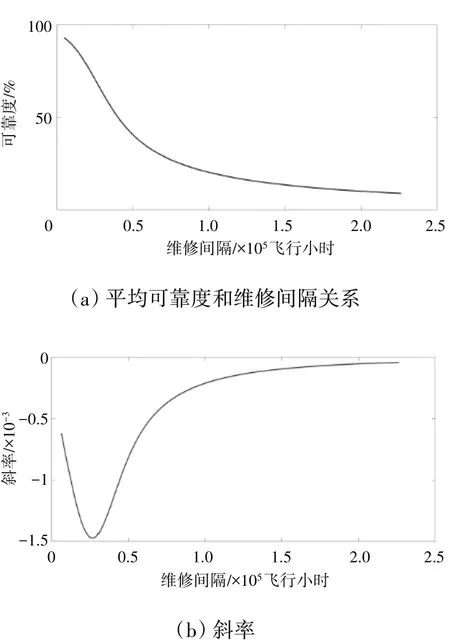
圖2 平均可靠度及斜率

經過計算得到“斜率圖”中極值點的維修間隔為26960 飛行小時。所以針對本機隊，起動機的軟時限設置為26960飛行小時。當起動機TSN達到26960飛行小時后，對其拆下送修。

此外，瞬時可靠度如圖3 所示。從圖中可見，起動機的瞬時可靠度會隨使用時間的延長而降低。為了保證部件的平均可靠度和航班的準點率，降低拆修成本和延誤成本，需要制定合理的部件維修策略。

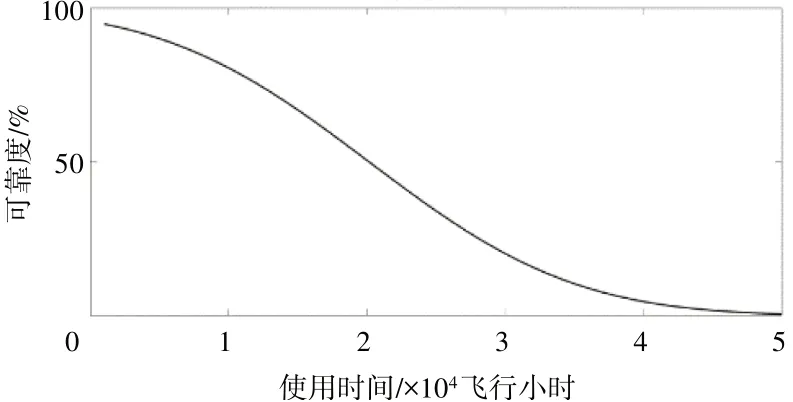
圖3 瞬時可靠度

在將數據按故障原因分類后，得到起動機故障的3 種主要原因，分別是“Bearing Failure”、“Decoupler”、“Oil Leakage”。計算得到3種故障原因的平均維修成本，結果見表3。從表中可見，在起動機失效的所有原因中，軸承失效（Bearing Failure）所帶來的維修成本是最昂貴的。

表3 各故障類型造成的平均維修成本

在起動機的實際運行環境中，滑油泄漏是導致起動機軸承失效的1 個內在原因。所以當滑油泄漏時，如果能及時發現并進行維護就可以一定程度減小軸承失效所帶來的高昂維修成本。由某航司調查報告得知，致使軸承失效的因素中約有10% 來自滑油泄漏。亦即當檢查出滑油泄漏并做了維護工作時，將會使軸承失效的概率減小10%。

此處滑油檢查及維護成本為b=100035.3，軸承失效的換修成本c=404671，引言中軸承失效的平均延誤成本約是d=200000。將數據代入式（14），則總期望損失為

維修成本函數圖像如圖4所示。函數只存在1個極值點，計算得出函數極小值為11964 元。最終得到針對滑油泄漏問題的最優檢查間隔為1915飛行小時。

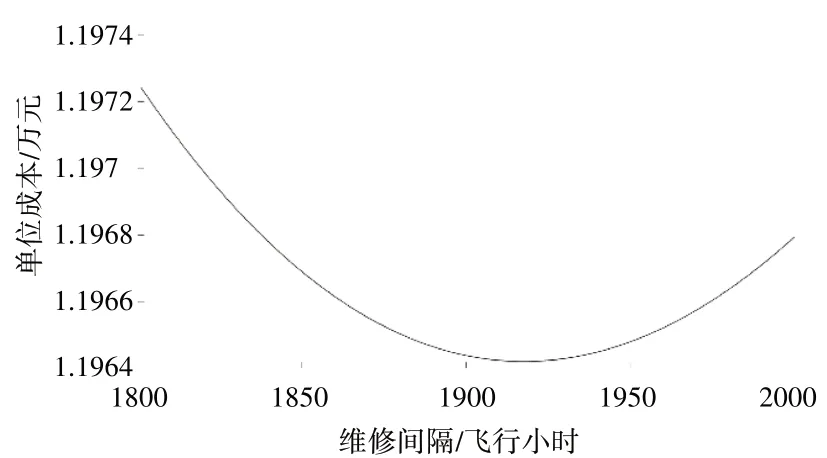
圖4 維修成本函數圖像

6.2 案例2

以波音737NG 飛機發動機的HMU（液壓機械組件）為例進行分析。針對HMU 共收集到51 組數據，在剔除無效數據并重新排序后，得到HMU 的歷史故障數據見表4。

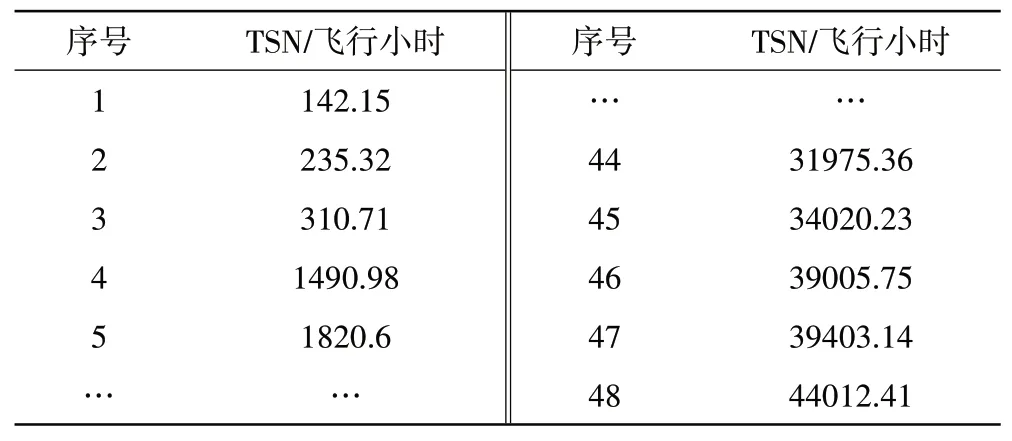
表4 歷史故障數據

按前文所述方法，計算得到威布爾分布的形狀參數β?=1.289，尺度參數η?=17781，D48=0.163。查表得D48.0.05=0.196。另外3 種分布的HMU 累積概率分布如圖5所示，參數估計值及檢驗水平見表5。

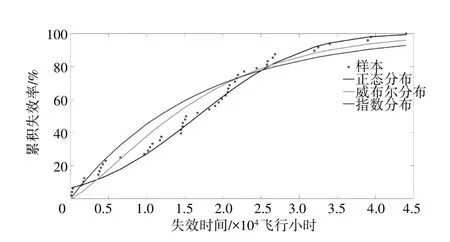
圖5 HMU累積概率分布

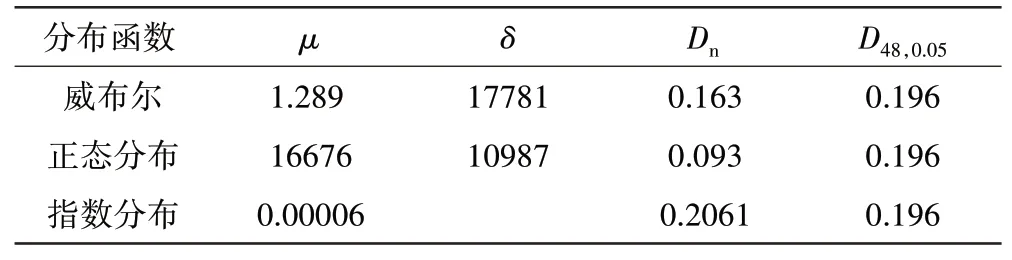
表5 參數估計值及檢驗水平

這里選擇圖像擬合效果最優且Dn最小的正態分布進行可靠性建模。由已知結果給出平均可靠度為

同樣以Tp為10 飛行小時為例，畫出平均可靠度與維修間隔函數圖及1 階導數圖，平均可靠度及斜率如圖6所示。

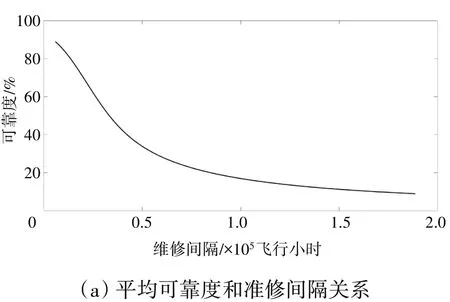
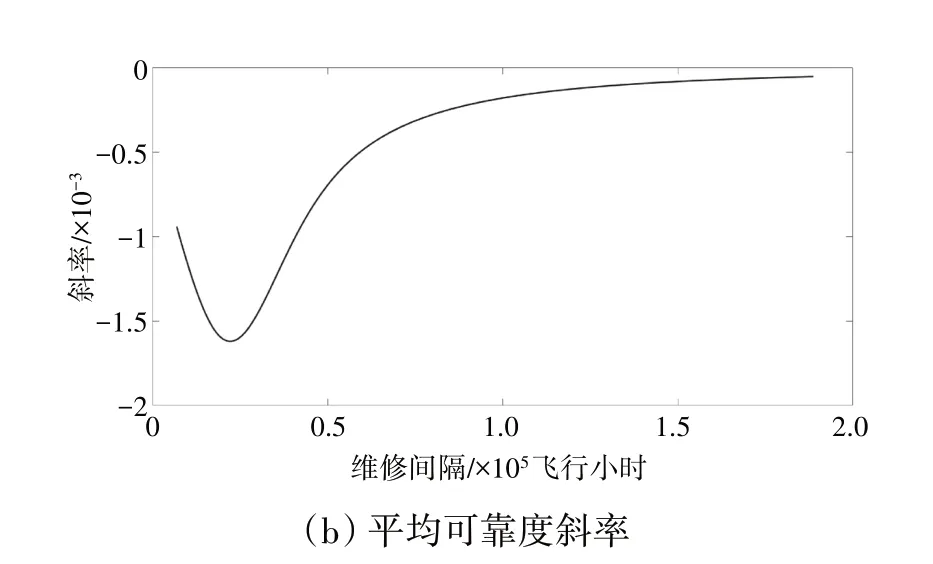
圖6 平均可靠度及斜率

最終計算得到極小值點對應維修間隔為22040飛行小時，即是HMU軟時限。

據資料顯示，某航空公司針對其737NG 機隊制定的HMU 的大修時限為25000 飛行小時，生產廠家建議737 機型的HMU 大修時限為30000 飛行小時。該航空公司下調了軟時限，目的是為了使其能更符合新一代737NG 飛機的實際運營情況。由此判斷本文制定737NG飛機HMU的軟時限合理。

7 結論

（1）目前航空公司根據各自機隊制定的起動機軟時限一般為10000~30000 飛行小時，HMU 軟時限約為25000 飛行小時。依據本文方法制定的起動機和HMU軟時限均在合理范圍之內；

（2）基于期望損失模型制定的起動機滑油泄漏檢查間隔為1915 飛行小時，參考各航司的標準亦在可接受范圍之內。