樓板假定對于平面凹進框剪結構抗震計算的影響

張元琦 中石油吉林化工工程有限公司 吉林 132002

框架剪力墻作為受力狀態復雜的結構形式，框架和剪力墻兩類抗側體系剛度相差較為懸殊，在水平地震作用下，樓板起到傳遞水平力、協調層間變形的重要作用，因而樓板的平面內變形及剛度對框剪結構抗震性能的影響不可忽略。常規結構計算分析中，一般采用樓板平面內剛度無限大的假定以簡化計算，在框架剪力墻的計算中往往存在較大誤差，以帶有狹長樓板或樓板不連續、不規則的框剪結構尤甚，其中平面凹進的框剪結構不僅顯著削弱樓板的平面內連續性，還使得位于邊榀的抗側體系不再完整，凹槽處水平地震作用沒有明確傳遞路徑，受力復雜，樓板應力集中明顯，并會造成結構質量和剛度不均勻不對稱，加重扭轉效應。本文以平面雙向均有凹進的框架剪力墻結構工程為例，研究此類結構在剛性/彈性樓板假定下地震動力響應、抗震性能的異同，為結構設計提供參考。

1 工程簡介及模型建立

某工程商用公寓樓為單塔大底盤結構，地下2層車庫，地上首層層高4 米，標準層層高3 米，建筑高度34 米。抗震設防烈度為8 度（0.2 g），Ⅱ類場地，抗震設防類別為丙類，建筑設計使用年限為50 年。由于首層嵌固，計算模型僅考慮地上部分，平面布置見圖1。

圖1 標準層結構平面布置圖

根據《結構設計統一技術措施》[1]，區分樓板開洞與平面凹凸的原則是：凹凸主要是建筑外立面的變化，考察結構在水平力作用下，結構抗側體系的完整性及在平面凹凸處的傳力路徑；樓板開洞則是從結構內部完整性角度，考察抗側力構件協同工作的能力。遇電梯井開洞處，宜將電梯井用剪力墻圍住，可視為樓板開洞，不作平面凹進。根據上述原則及規范對建筑平面凹凸的規定，該工程Y 向凹進4 m，凹進程度4/11=0.36 ＞0.3，為一般平面不規則結構。

該建筑疏散步梯梯板采用滑動支座與梯梁連接，計算中不計樓梯剛度，僅作為靜力荷載。

根據《高規》[2]7.1.4 規定，剪力墻結構底部加強部位從地下室頂板算起，高度為max{H/10，底部2 層}，一、二層剪力墻為一般剪力墻-加強位置。罕遇地震波選取Pacoima1 波，《抗規》[3]第5.1.2 條和第5.2.3 條規定，限定最大峰值加速度220 cm/s2，地面時程以X 為主向，主次向加速度比值指定為1 : 0.85，地震持續時間取15 s，加速度時程見圖2。

圖2 Pacoima1 波加速度時程

2 模型初始設定

建筑東西兩側凹進2 m，凹進率13.3%<30%；南側凹進4 米，凹進率36%>30%，為平面一般不規則結構。將工程項目結構原型建入midas gen，記為MOD-0，結構模型立面見圖3。

圖3 MOD-0 立面示意

3 單元類型特性指定及構件材料

（1）墻單元：墻為板殼單元并考慮真實厚度。塑性鉸選擇鋼筋混凝土纖維模型，靜力及小震分析完成后更新剪力墻配筋信息，然后定義非彈性材料特性值，由程序自動生成纖維鉸模型。砼本構選擇《混規》[4]附錄C 單軸受壓本構模型（過-王準則），鋼筋本構選擇二折線模型，二段折線斜率取b=0.01。

（2）框架：gen 在前處理階段不區分梁柱，均視作一般線單元；若梁柱采用纖維鉸模型則迭代結果收斂性不佳，故梁柱均采用傳統集中鉸設定。框架柱受壓彎作用，塑性鉸定義為P-M-M 相關，滯回模型為修正武田三折線。修正后的三折線模型對屈服段及卸載狀態予以一定校正，修正后承載能力較三折線模型略有下降，滯回曲線更為飽滿，耗能能力更強（材料本構及滯回模型曲線見圖4）。

圖4 材料本構及滯回模型曲線

剛度退化曲線中，第一剛度折減系數α1=0.5，第二剛度折減系數α2=0.1，P1 對應開裂階段起點荷載，P2 對應屈服階段起點荷載。

4 剛性假定計算偏差

根據分析結果，將初始模型MOD-0 設置為剛性樓板假定/彈性樓板假定兩個子模型分別進行小震彈性分析，整理結構動力特性、凹槽處典型豎向構件內力及位移結果，見圖5 及表1。內力分析結果為X 向小震單工況內力標準值，兩種假定下Y向地震內力計算結果相差甚微，故未列出。

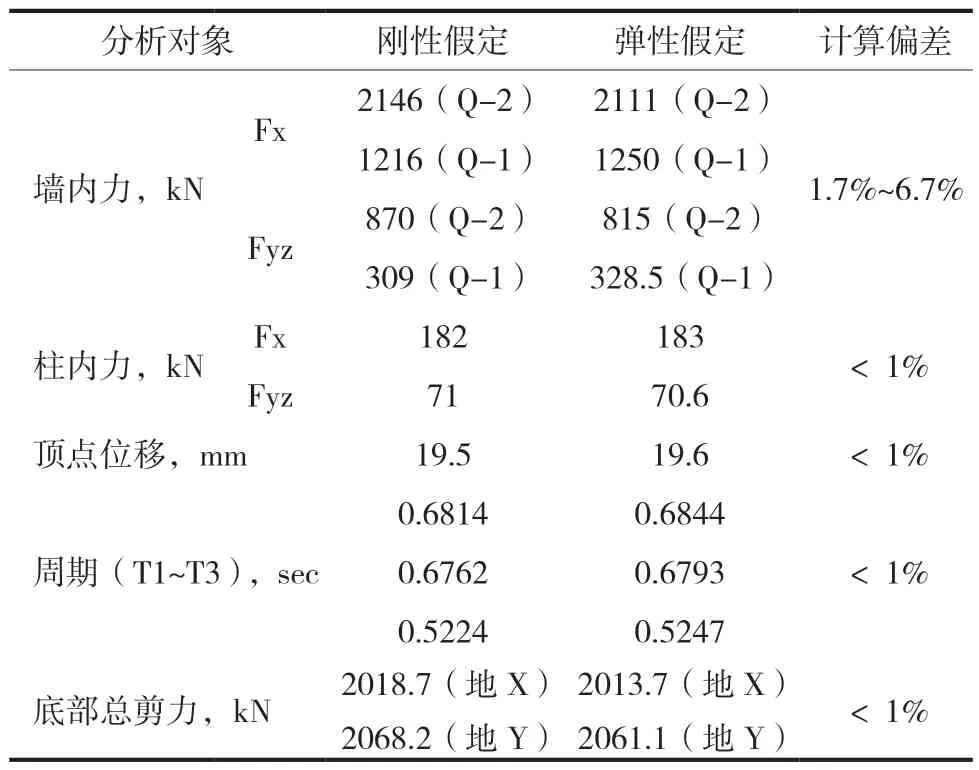
表1 彈性分析結果

結果表明，在小震彈性工況下，除電梯井的X向單片墻外，構件內力分配、結構動力特性及變形，兩種假定計算差異不大；樓板假定對彈性層間位移影響甚微，可以忽略不計。由于結構平面布置中剪力墻間距、板跨較小，雖然樓板存在開洞，但仍保持較大平面內剛度，在地震作用下未產生明顯的平面內變形。

整理MOD-0 在罕遇地震下，兩種假定的對比結果，見表2 及圖6。

圖6 罕遇地震層間位移角及層間剪力對比

可見兩種樓板假定在罕遇地震作用下計算結果有一定偏差，各層地震剪力存在3.3%~6.5%的偏差；彈塑性層間位移最大值出現在4、5 兩層，計算偏差分別為4.6%、5.4%。采用剛性樓板假定時，結構抗側剛度偏大，因此，盡管剛性假定下地震剪力計算結果偏大，但產生的層間位移仍小于彈性假定結果。頂層屋面板絕對水平位移見圖7。

圖7 頂層屋面板水平位移絕對值

位移等值線分布大體相當，但彈性模型在南側凹槽處樓板端部產生0.6 mm 相對位移，說明樓板在罕遇地震作用下產生一定平面內變形。

剪力墻塑性鉸出鉸部位及屈服狀態見圖8~圖9，取step：20s 的最終狀態，鉸成分指定平面內彎曲Ry。

圖8 非彈性鉸屈服狀態

可見兩組模型剪力墻出鉸部位大體一致，以中部梯井根部塑性發展為最多，且各剪力墻屈服部位主要集中于底部加強2 層；兩組模型墻鉸屈服程度有較大區別，墻肢Q-2 在剛性模型中，底部兩層延性系數為5.5/4.7，彈性模型為5.9/5.3；取4 片Q-1墻根處延性系數最大值，剛性模型為3.7/2.8，彈性模型為4.0/3.4，剛性假定下整體結構的剪力墻屈服程度小于彈性假定。故彈性假定下，剪力墻有更大塑性發展，剛度退化更多，從而進一步證明，彈性假定大震剪力較小、而位移結果反而偏大。

5 結語

對于本工程平面凹進的框剪結構，剛性樓板假定和彈性樓板假定在小震彈性計算分析中影響不大，當凹進程度不大（如算例中的Y 向地震）、剪力墻間距較小時，樓板平面內剛度較大，兩種假定計算差異可忽略不計；但在罕遇地震工況下，剛性樓板假定下的分析結果無論位移指標、塑性發展程度均小于彈性假定，計算結果偏向于不安全，且該假定高估結構在彈塑性階段的抗側剛度，故該類型框剪結構涉及大震計算時，應慎用剛性樓板假定。

圖9 非彈性鉸延性系數（D/D2）