基于深度學習的數學教學策略研究

李余芳

【摘要】深度學習，即為教師科學引導學生進行知識的自我深度理解，學生自主循序解決復雜難懂問題的過程即為數學核心素養構建的過程.深度學習即是實現課程改革、發展核心素養的有效路徑.本文對高中數學三角函數深度學習策略開展研究，旨在以此方式為教師開展系列教學時提供更具價值的參考標準，從而提高學生綜合能力，培養學生高階思維.

【關鍵詞】深度學習；高中數學；三角函數

深度學習并非一蹴而就的，而是循序發生的過程，需要教師循序引導，帶領學生進入最佳狀態，開展系列學習.同時，高中三角函數內容更是高考的重點內容，更需要教師持以足夠的耐心，引導學生實現深度學習.

1?巧設教學目標，把控教學方向

基于深度學習的數學教學設計時，首先，教師需精細化、深入性研究教材內容及課程標準，制定相匹配的教學目標.新課程標準明確指出：促進學生發展的系統教學，需要教師持以整體性教學觀念，立足于整體視角之下設立教學目標.深度學習將更注重知識的系統整合及有機構建，同樣更強調教師整體觀念.教師只有具備一定的整體教學觀，方可構建起更為系統、全面、整體的數學課堂，保障學生在自主學習過程中，構建起更為完整、全面的知識鏈條、知識架構.因此，基于深度學習的數學教學，需立足于整體性角度上，幫助學生掌握系統知識.

教學目標確立之前，教師需確立該單元系統.單元大小并沒有統一規定，為此，教師可通過教材內容出發，也可以要從數學核心知識角度出發，確立單元內容.單元教學目標的確立既需要整體性單元目標，又要細化課時目標.整體性單元目標則是涉及到學生素質培養、數學思想培養、高階思維培養等諸多方面，課時目標則是前者的具體化內容，是在整體方向之下，依據相關教學內容制定的學生所需掌握的能力、知識、素養目標.因此，在教學目標制定過程中，需綜合教學課程標準，把控教材相關要求，注重學生對其學科知識、思想方法的掌握理解，并在系統單元落實中更科學地實現教學任務.

例如?以“三角函數”單元教學為例，在進行教學目標設計時，需明確三角函數在教材內容占比及其重要程度.在確立基本三角函數相關教學內容，就其三角函數系列內容即可設置相關的教學目標：（1）掌握三角函數系列預備知識：明確擴充角、周期，理解弧度制；（2）以圓周角度出發，深度探索正余弦函數相關定義及基礎形式，對其正切函數予以類比研究，并掌握y=cosx、y=sinx在0，2π的相關圖象表示及具體性質；（3）結合具體實例深入研究：y=Asinx（ωx+φ）的具體圖象變化，明確其中的參數意義，回歸簡單實際的問題，精細刻畫該事物變化模型；（4）系統研究三角函數恒等關系：二倍角、同角、兩角和差.

2?整合數學教材，更新教學內容

教材既為教學主體，同樣也是學習內容基礎載體.教學核心內容都是根據教材內容所制定，同時教材也是國家標準規劃的，所面向群體復雜，個體差異性顯著，因此難以兼顧到各個學生、各個學校的實際情況.為此，為了能夠將教材實際使用價值得以充分發揮，教師就需對課程內容予以系統整合.首先，需綜合考慮到教材外部要素，即學校資源、教師資源、學生資源.教材整合旨在更好地服務于學生，因此，教材整合內容需依據學生具體接受程度來設定.普通學生則是以數學基礎內容為重心，重在激發學生學習興趣.拔高學生側重在拓展，實現針對性進步；其次，教材內部因素，例如教學實例及教學情境的開發.教材課本實例同情境內容都是年年延續，久未改變.其中很多實例題目同現實生活完全脫節，數據信息也未及時更新，極易引發學生的學習陌生感.因此，教學準備階段，教師需深度挖掘該教學案例同教學情境背后的內容，充分保留經典，在不改變原則的基礎上適當修改.

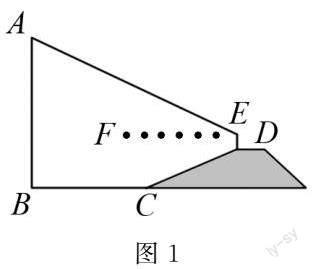
例如?針對三角函數典型例題，如圖1所示，垂直于水平面的三角形建筑物，為測量AB高度，小明自建筑物底端B點出發，走52km，走到C點，而后沿CD前進，直至到達頂坡D點處，BC=DC，在該D點位置進行測量，DE高度8km，E點處測得該建筑物頂端A點仰角為27°，點A，B，C，D均為同一平面內，斜邊CD坡度比為i=1∶2∶4，求AB高度.

該案例教學中，可以發現步行52km不太現實，所以極易引發學生的不現實感.為此，教師需及時更新相關單位、數據內容，將其更換為52m，方可讓該例題增添真實感.此外，教師還需適當豐富教材內容，不僅僅是增添些許相關知識內容，更要適當融入數學文化、數學素養等此類精神層次內容.該內容的增添，將引導學生更深入理解該數學內容的實際價值，促使學生及時獲取數學知識，培養數學能力，豐富數學解題經驗.以三角函數教學為例，教師為了讓學生更明確三角函數的使用意義，可在課堂教學時，適當講解三角函數的發展史，讓學生感受古人智慧，讓學生感受到探索數學知識過程中的驚喜.

3?預評估教學推進，激活學習狀態

3.1?開展預評估模式，明確最近發展區

依據相關數據調查顯示，大多學生在學習新知識時會聯系舊知識.教師作為學生學習的引導者、促進者，更要在日常教學時，幫助學生在新舊知識串聯中，搭建有效紐帶.在此工程中，教師需明確學生原有認知水平，既可對新知識起到一定的促進作用，也能起到些許的啟發作用.因此，教學準備階段，教師就需落實預評估工作，以此方式深度了解學生知識水平、知識儲備量，并密切關注學生極易出錯的環節.此外，預評估工作也將更進一步明確學生最近發展區.深度學習將緊密圍繞極具挑戰性主題，然而其挑戰“天花板”與學生之間的距離時，教師教學設計環節的基礎依據，因此，教師需保障學生發展在科學范圍內推進.

預評估內容主要有教師評估、學生自評兩方面組成.教師評估則是依據教師教學經驗及對學生的了解情況進行評估，為了提高評價精準度和評估效率，教師即可通過大數據、互聯網手段進行全面分析.例如，一些網絡批閱作業的軟件，它不僅更精細化分析學生考試各個環節得分情況，也將同學生以前考試成績進行對比分析，立足于諸多維度全方位剖析學生具體學習情況.學生自測則需依靠學生的自主學習，教師可設置三角函數的相關導學案，引導學生循序了解自己的預習效果，明確學習難點，及時開展針對性優化.

3.2?循序激活狀態，創設主動學習氛圍

首先，教師需明確深度學習主體在于學生，學生學習參與度將直接決定學習效果.為了提高學生的參與度，就要善于激發學生內部學習動機，在實際教學中，教師則要創設出主動學習課堂氛圍.在此過程中，教師需明確，教學氛圍質量并非以課堂熱鬧程度為標準，而是以學生實際行為狀態同當前學習情境的配合度為前提.學生主動學習習慣也并非是一朝一夕即可養成的，而是需要教師在日常教學中有意識地培養.學生主體意識將直接決定學生主動學習的效率和學習頻率，只有學生將自己作為學習的主人翁時，才能自然形成主動學習氛圍，教師則需及時開展系統調節.如若學生并不具備主體意識，主動學習氛圍也是表面形式，將在教師要求下成為被動.因此，教師教學出發點即為學生個人需求，讓學生參與教學過程就具備決定權，強化學生學習過程的主人翁意識.

其次，教師則注重民主師生關系的建立.師生關系作為社會關系最為特殊復雜的一種，將是讓學生放松狀態，實現深度學習的重要影響因素.教師要積極與學生構建起民主型關系，創設出互助、平等、開放的相處模式，盡可能地多鼓勵、多表揚學生，增強學生自信心，激發學生興趣，以此方式，將幫助學生快速進入深度學習狀態.

4?構建教學情境，實現深度學習

4.1?立足現實條件，呈現真實體驗

開門見山式的教學，較難以激發學生的積極性.因此，急需構建有效有趣的情境，幫助學生快速進入狀態，以此狀態不僅激發學生的學習興趣，也將快速引導學生思維開展深度思考.首先，教師需立足于現實條件，帶給學生更為真實的體驗.綜合深度學習內涵及數學核心素養相關要求，高中數學系列教學必須在真實學習情境基礎上開展，引導學生在基礎知識儲備之上，挖掘學習內涵，自主透過生活情境獲取價值信息.教師需綜合考慮數學學科本質特性，并以學生實際生活為基礎，構建出更為真實的教學情境，為學生后續學習問題提供有效“腳手架”，幫助學生掌握更深層次知識內容，理解更復雜的概念定義，開展深度學習.

例如?在三角函數：y=Asinx（ωx+φ）圖象理解時，教師即可將生活中摩天輪經歷構建教學情境.為此，教師可以附加視頻豐富學生的體驗感.通過以國內最大摩天輪“南昌之星”為例，該摩天輪最低點距離地面7m，直徑153m，共計設有60個太空艙，各個太空艙最多可容納8人.忽略其他因素影響，將其摩天輪運轉活動視為勻速運動，每旋轉一周需歷經30分鐘，上艙起點即為該摩天輪最低點，經過t分鐘后抵達B點，求B點距地面的高度H=f（t）.以此方式，將帶領學生進入更為真實的現實世界中，讓學生放松神經，沉浸于教師所設置的情境問題中自主探索.

4.2?巧設教學問題，引申深度思考

淺層學習則是低階基礎性思維的思考過程，更傾向于死記硬背記憶方式掌握相關知識，難以依據實際問題的具體開展情況，靈活運用法則公式及其他數學知識.深度學習則是在其低階基礎性思維基礎之上，指向高階思維，將透過數學問題挖掘相關概念原理，并在問題解決的過程中始終持以積極樂觀的態度.以此對比可見，深度學習核心在于問題的解決.因此，教師不僅要注重教學情境的真實度，更要全面挖掘、深入分析教材內容，同時設置更具啟發性思維的深度學習相關問題.并且，問題的設置需具備層次性特點，引導學生思維發散得以由低至高，層層遞進，層層發散.因此，層次性不僅體現為該問題的表現難度，更體現出其啟發性和靈活度.

例如?在學習“三角函數”時，教師可拋出“現實生活中，運用三角函數‘勾三股四玄五’定理的現象有哪些？”面對該問題，學生首先會懵住，這時教師則要循循善誘引導學生，“勾三股四弦五”作為勾股定理的典型例子，其原理在于直角三角形中，兩條直角邊分別為3、4時，其斜邊則為5.在實際生活中，常在工程案例中應用，是驗證兩條線是否垂直的有效措施，鑒于人工操作誤差較大，因此距離較大時常用儀器檢測，距離較小則利用勾股定理檢測.該問題看似較為簡單，但是略加思索就需要綜合考慮多方面因素，既在其知識層面上引出三角函數內容，也凸顯勾股定理特征，能力層面上，也將引導學生利用數學思維解決生活問題.

5?結語

綜上所述，基于深度學習的數學教學策略.首先，教師需精細化、深入性研究教材內容及課程標準，制定相匹配的教學目標；其次，需綜合考慮到教材外部要素，即學校資源、教師資源、學生資源.學校資源，即為綜合學校特點及當地特色，開發國家相關課程，以此多樣化、多角度地培育學生；再次，教學準備階段，教師就需落實預評估工作，以此方式深度了解學生知識水平、知識儲備量，并密切關注學生極易出錯的環節；最后，需立足于現實條件，帶給學生更為真實的體驗.

參考文獻：

[1]朱嘉怡.基于深度學習的高中數學建模教學研究[D].上海：上海師范大學，2022.

[2]李保臻，孟彩彩，鞏鎧瑋.基于深度學習的高中數學教學設計：基本要求及優化策略[J].內江師范學院學報，2022，37（02）：1-5.

[3]譚云.基于深度學習的數學課堂教學研究[D].長春：長春師范大學，2020.

[4]羅穎.基于深度學習的高中數學課堂教學設計研究[D].南昌：江西師范大學，2020.

[5]薛志宏.高中數學教學中促進學生深度學習的研究[D].開封：河南大學，2020.