基于區域中心溫度場預測的回流焊接優化仿真

隋 遠,卜凡洋,邵子龍,閆 偉

(山東師范大學信息科學與工程學院,山東 濟南 250014)

1 引言

元件焊接技術是集成電路板等電子產品生產過程中的一項重要工藝,通過加熱元器件達到錫膏熔點后,在液態錫表面張力及助焊劑的作用下錫液回流到元器件引腳上形成焊點,進而完成將線路板焊盤和元件焊接成整體的任務。

實際焊接過程中,工業界往往采用回流焊接工藝,即使用回流焊爐設備,將待焊接元器件傳送經過多個不同溫區,使錫粉完成由固態到液態再到固態的轉換,此過程中錫膏在助焊劑等材料的催化下,融化(錫膏熔點:217℃)形成一層薄薄的錫珠,在其表面張力的作用下,聚集在元器件焊點表面,經冷卻區制冷凝固,實現焊接。回流焊接作為集成電路板生產中的關鍵工序,合理的溫度曲線設置是保證回流焊接質量的關鍵[1]。回流焊接的控制實質上是對溫度工藝參數的控制[2],不恰當的溫度工藝參數設置會使PCB板出現焊接不全、虛焊、元件翹立、焊錫球過多等焊接缺陷,影響產品質量[14]。

目前,關于溫度場工藝參數設定大多通過多次重復實驗測試進行控制和調整,測試人員使用傳感器等設備獲取溫區溫控曲線,憑借操作人員經驗觀察得出這條曲線反映的能量作用量以及能量作用點,并依次調整溫度場工藝參數。產品質量的好壞直接受到操作員經驗的影響。現有的僅通過實驗獲得符合工藝要求的最佳溫度的方法不僅低效,而且在每次實驗僅只能獲得一組爐溫曲線的數據,樣本量小,測試結果缺乏普適性,極大的浪費了人力財力物力。

為優化回流焊接工藝參數的調控方法,國內外學者進行了相關研究。目前回流焊溫度曲線仿真與預測系統主要以F.Sarvar[6]為代表,提出了部分以機理模型為主要切入點的優化方法[9],[10],徐宗煌[8]提出了一套基于牛頓冷卻定律的微分方程的爐溫曲線優化模型;席晨曦[11]在微分方程的基礎上引入模擬退火算法輔助爐溫曲線優化設計;國內的龔雨兵通過數值建模與仿真提出了一種優化的回流焊溫度曲線控制;饒庶民[7]在回焊爐溫度控制模塊的基礎上,分析了實際溫度場變化規律,使用有限元分析軟件對回焊爐內的溫度進行仿真分析,可以很好的對溫度場進行擬合預測并開發了一套適合回焊爐曲線分析的軟件;對于實際回流焊接溫度曲線設置,姜海峽[15]論述了回流焊接溫度曲線的設置與測試方法,通過對比分析,可調整參數至更加理想的回流焊接溫度曲線馮志剛[3]量化了回流焊接工藝參數對溫控曲線的影響;張輝華[5]提出了一套面向混裝氮氣回焊爐的溫度曲線控制方案。

為解決傳統實驗測試方法的弊端,本文采用機理模型進行分析研究,提出一種回流焊接區域中心溫度場預測模型,實現區域中心溫度場工藝參數的預測優化,并針對特定工業生產場景下的實際需求設計了一套回流焊接優化策略:溫度參數已知情況的速度區間預測策略,錫膏融化回流面積最小參數區間預測策略,錫膏融化回流面積左右最對稱參數區間預測,能夠極大的優化生產過程、節省設備調試時間、優化生產產品焊點質量。

2 基于常微分方程的回流焊接區域中心溫度曲線預測模型

2.1 模型定義

通常情況下,回流焊爐內部設置若干個小溫區,它們從功能上可分成4個大溫區:預熱區、恒溫區、回流區、冷卻區(如圖1所示)。某回焊爐內有11個小溫區及爐前區域和爐后區域(如圖1所示),每個小溫區長度為30.5 cm,相鄰小溫區之間有5 cm的間隙。其中小溫區是指具有加熱功能的某一連續加熱區間,間隙是指沒有加熱源的某一連續區間,大溫區是指由小溫區和間隙組合而成的某一連續區間。實驗條件下的回焊爐實際尺寸如表1所示。

表1 某回焊爐內含有11個小溫區及爐前區域和爐后區域的具體尺寸

圖1 回焊爐截面示意圖

參數可調節范圍如表2某回焊爐的可調節參數范圍所示。

表2 某回焊爐的可調節參數范圍

在設定各溫區的溫度和傳送帶的過爐速度后,可以通過溫度傳感器測試某些位置上焊接區域中心的溫度,稱之為爐溫曲線(即焊接區域中心溫度曲線)。實際生產時可以通過調節各溫區的設定溫度和傳送帶的過爐速度來控制產品質量。在上述實驗設定溫度的基礎上,各小溫區設定溫度可以進行±10℃范圍內的調整。調整時要求小溫區1～5中的溫度保持一致,小溫區8～9中的溫度保持一致,小溫區10～11中的溫度保持25℃。傳送帶的過爐速度調節范圍為65～100 cm/min。

在回焊爐電路板焊接生產中,各溫區中心溫度場變化應滿足一定要求,即制程界限(見表3)。

表3 區域中心溫度場變化制程界限

2.2 模型建立

假設焊接區域中心看作質點、焊接系數受溫度的影響忽略不計、各加熱區設定溫度即是對應區域爐內溫度、焊接過程不考慮熱對流。根據熱傳導規律(1)以及比熱容式(2)對比得出,小溫區焊爐內環境溫度與焊接中心區域溫度的一階常微分方程(3)

(1)

(2)

(3)

(4)

2.2.1 回流焊爐爐內溫度場分布函數T(x)

由于回焊爐相鄰小溫區之間爐內環境溫度場分布符合Sigmoid函數(5),利用此規律,得到平滑的溫度過渡曲線如圖2所示,曲線兩端是恒溫區,中間是無加熱源的爐內環境溫度區,此時Sigmoid函數經過平移變換、伸縮變換后得到T(x)解析式(6)

圖2 兩端是恒溫區,中間是無加熱源的爐內環境溫度區間過渡曲線

(5)

(6)

針對小溫區與小溫區之間溫差過大的特殊間隙,利用式(4)所述一階常微分方程推理可知,焊爐內環境溫度T(x)與焊接中心區域溫度f(x)溫差越小,其焊爐內環境溫度T(x)的一階導數越小,因此在TT4=255℃,TT5=25℃且環境溫度也為25℃的條件下,凹函數存在下降趨勢,由于溫差的不斷縮小,T(x)的一階導數也不斷減小,此時焊爐內環境溫度T(x)必然為凹函數。利用位移與焊爐內環境溫度T(x)的直角坐標系易知坐標[x前,TT4],[x后,TT5],代入一階線性函數可得(7),代入指數函數可得(8),由式(7)(8)可以得到爐內環境溫度的線性表達式(9)。

(7)

(8)

T(x)=p·T1(x)+(1-p)·T2(x)

(9)

通過遍歷參數p,可以確定當p=0.8時方差最小,不同參數p下爐溫曲線與擬合曲線方差見表4。

表4 爐溫曲線與擬合數據在不同p下方差

因此,得到爐內環境溫度場分布函數如下表5。

表5 爐內環境溫度場分布函數

2.2.2 最優焊接系數Q預測

利用傳感器等工具,測得得焊接區域中心溫度曲線f(x)。將f(x)與爐內環境溫度分布T(x)代入式(4)中,設置各個小溫區的溫度參數以及傳送帶過爐速度,并將前一區間預測的f(x)的溫度末值賦值給后一區間預測的溫度初始值,使用四階龍格庫塔法,顯式迭代非線性常微分方程,求解出各個位置的解常微分方程的函數值。

通過遍歷焊接系數Q,利用作方差等方法挑選出與實驗中測得焊接區域中心溫度曲線f(x)最為相近的一組溫度曲線,確定并評價最優焊接系數并繪制預測曲線。實驗顯示得出Q=-0.021時方差最小,不同參數Q下爐溫曲線與擬合曲線方差見表6。

表6 爐溫曲線與擬合數據在不同Q下方差

3 回流焊接方法優化策略

根據2提出的基于常微分方程的回流焊接區域中心溫度場預測模型,針對特定工業生產場景下的實際需求設計了一套回流焊接優化策略如下:①預測設定溫度參數下的速度區間;②預測錫膏融化時回流面積最小參數區間;③預測錫膏融化時回流面積左右最對稱參數區間;

3.1 預測設定溫度參數下的速度區間

各溫區溫度設定條件下,利用建立的焊接區域中心溫度場預測模型,對速度從小到大每隔0.1cm/min進行遍歷,在所有溫區溫度確定、焊接中心溫度曲線唯一的條件下可以找出符合表3制程界限的最大傳送帶過爐速度,加快工業生產速度。制程界限如下:

對于界限條件(1)、(2),要求升降溫速度不超過3 ℃/s,判斷是否滿足

(10)

對于界限條件(3),找到150℃和190℃對應的t1和t2,判斷是否滿足

60≤t2-t1≤120

(11)

對于界限條件(4),找到焊錫熔點溫度對應的t1和t2,判斷是否滿足

40≤|t2-t1|≤90

(12)

對于界限條件(5),找到f(x)的最大值Tmax,判斷是否滿足

240≤Tmax≤250

(13)

通過枚舉速度,將焊接區域中心溫度曲線T(x)離散化抽樣保存到數組中,判斷是否滿足制程界限(10)～(13),記錄速度區間并輸出。

3.2 預測錫膏融化時回流面積最小參數區間

3.3 預測錫膏融化時回流面積左右最對稱參數區間

各溫區溫度設定條件下,利用建立的焊接區域中心溫度場預測模型,對速度v、各溫區溫度設定值TT1,TT2,TT3,TT4進行枚舉,計算對應的焊接區域中心溫度場變化f(x)。

4 仿真與分析

為了證明基于區域中心溫度場預測的回流焊接模型的有效性,在Matlab環境下進行仿真測試。爐內環境溫度變化T(x)和某次實驗中測得的焊接區域中心溫度場變化f(x),如圖3所示,傳送帶的過爐速度為70cm/min,爐溫各溫區溫度設定如下:175℃(小溫區1～5)、195℃(小溫區6)、235℃(小溫區7)、255℃(小溫區8～9)及25℃(小溫區10～11)。

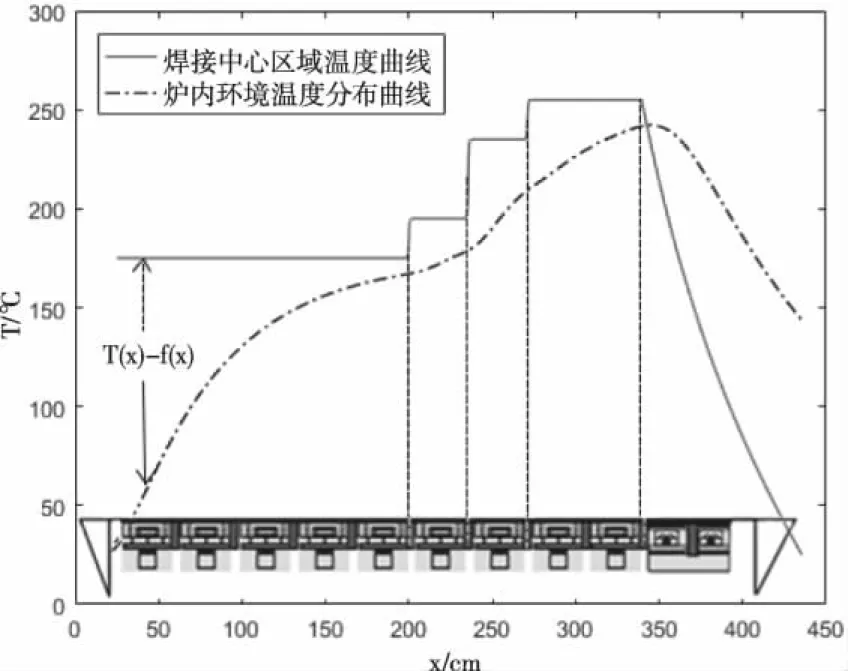
圖3 爐內環境溫度變化和某次實驗中測得的焊接區域中心溫度場變化示意圖

圖4為隨機實驗中,焊接區域中心溫度曲線與不同焊接系數Q預測的對比圖,發現當Q=0.021時,預測效果最佳。當最佳焊接系數Q值確定后,任意條件下的焊接區域中心的溫度變化情況都可以確定。

為進一步說明本方法的可靠性,使用皮爾遜系數,由表7可知當Q=0.021時,擬合數據與真實爐溫曲線高度吻合,皮爾遜系數高達99%,表現出極強的相關性,預測結果如圖5所示。

表7 實際的爐溫曲線與擬合出的爐溫曲線在不同Q下的方差與皮爾遜相關系數

圖5 某次實驗焊接區域中心溫度曲線與最優焊接系數Q=-0.021溫度預測的對比圖

5 結論

傳統回流焊接工藝參數設定時多采用實驗測試的方法,存在著低效、耗時、設定結果強依賴經驗等問題,因此,本研究采用一種機理模型對該問題進行分析研究,提出一種回流焊接區域中心溫度場預測模型,實現焊接區域中心溫度場工藝參數的預測優化:根據熱傳導規律以及比熱容公式,得到焊接區域中心溫度曲線關于爐內溫度分布函數在傳送帶位移上的一階常微分方程,對于溫差較小的間隙,使用Sigmoid函數,得到平滑的區間溫度過渡曲線;對于溫差較大的間隙,利用指數函數和一次函數進行線性組合,迫近實際凹函數,從而得到完整的爐內溫度分布函數。通過求解常微分方程得到焊接參數,并通過計算預測溫度場與真實溫度分布數間的均方誤差優化模型參數,得到一組符合制程界限的最優工藝參數。

同時,根據上述建立的基于區域中心溫度場預測方法,針對特定工業生產場景下的實際需求設計了一套回流焊接優化策略:給定溫度參數下速度區間預測策略,錫膏融化回流面積最小參數區間預測策略,錫膏融化回流面積左右最對稱參數區間預測。

仿真結果表明本方法得到的區域中心溫度場預測結果與實際傳感器數據高度吻合,具有很強的相關性。因此,本方法可以極大的優化回流焊接生產過程,節省設備調試實踐,優化生產產品焊點質量。