點點關注　步步有據

陳波

不少同學常常有這樣的疑惑：為什么自己的成績會比預估分數低很多？究其原因，大多數是答題不規范所致。現以兩道中考題為例，介紹答題要求和規范，從而幫助同學們不僅“做得對”，而且“得分全”。

例1 （2022·江蘇鹽城）證明：垂直于弦AB的直徑CD平分弦以及弦所對的兩條弧。

【分析】本題滿分為10分。垂徑定理的證明過程需要同學們對命題的條件、結論等概念有充分的理解，以及能靈活運用“三線合一”定理、圓心角相關知識，考查了大家的數學抽象、邏輯推理等核心素養。整個證明過程包括補全圖形、寫出已知和求證、給予證明等過程，每完成一步都會得到相應的分數。

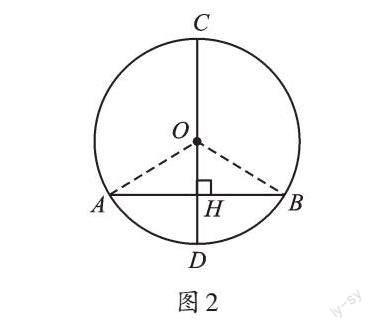
已知：如圖2，AB是⊙O的弦，CD為⊙O的直徑，且CD⊥AB，垂足為H。（2分）

求證：AH=BH，[AC]=[BC]，[AD]=[BD]。（4分）

【說明】同學們一定要分析清楚原命題中的條件和結論，答題到此可以得到4分，包括：補全圖形1分、結合圖中字母寫出已知條件1分、三個結論都寫出2分（如有漏寫扣1分），接下來的證明過程累計6分。

證明：連接OA、OB。（1分）

∵OA=OB，OH⊥AB，（2分）

∴AH=BH，∠AOD=∠BOD。（3分）

∴[AD]=[BD]。（4分）

∵180°-∠AOD=180°-∠BOD，

即∠AOC=∠BOC，（5分）

∴[AC]=[BC]。（6分）

【說明】很多同學在書寫證明過程時不愿意寫輔助線作法，這樣OA、OB的出現就顯得很突兀，會被扣分；由∠AOD=∠BOD可以得到[AD]=[BD]，想得到[AC]=[BC]需通過證∠AOC=∠BOC，也可以用[CAD]-[AD]=[CBD]-[BD]得證，證明過程需完整，否則也會被扣分。

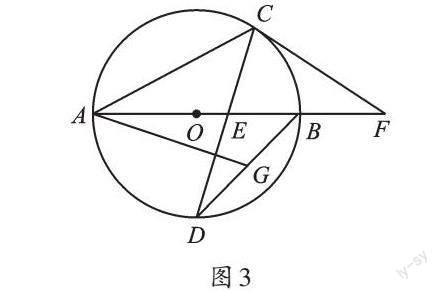
例2 （2022·江蘇蘇州）如圖3，AB是⊙O的直徑，AC是弦，D是[AB]的中點，CD與AB交于點E。F是AB延長線上的一點，且CF=EF。

（1）求證：CF為⊙O的切線。

（2）連接BD，取BD的中點G，連接AG。若CF=4，BF=2，求AG的長。

【分析】本題滿分為8分，考查了綜合運用圓的基本性質、切線的判定、勾股定理等知識的能力。下面是詳細的解題過程，請同學們思考每一個得分點。……