一道教材例題的“變身”

尹雪蔓

數學解題不應只局限于一道題目的本身，而應能比較類似的題目，用變化的眼光去發現它們之間的聯系，在比較中深化對知識的理解，掌握解題方法，提高舉一反三和靈活應變的能力。

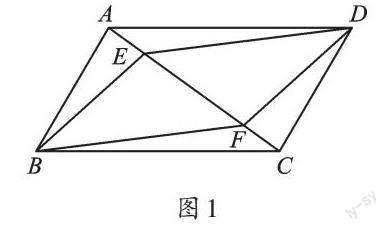
原題呈現 （蘇科版數學教材八年級下冊第69頁例3）已知：如圖1，在?ABCD中，點E、F在AC上，且AE=CF。求證：四邊形EBFD是平行四邊形。

【分析】我們可以利用“平行四邊形的性質→尋找三角形全等→線段和角相等→判定平行四邊形”的思路解決問題。

證法一：根據平行四邊形對邊相等的性質定理可知AB=CD，根據平行四邊形的定義可知AB//CD，所以∠BAE=∠DCF。又因為AE=CF，所以△ABE≌△CDF（SAS），所以BE=DF，∠BEA=∠DFC。根據“等角的補角相等”可得∠BEF=∠DFE，所以四邊形EBFD是平行四邊形。

證法二：同“證法一”可證得BE=DF。同理，通過證明△ADE≌△CBF（SAS）得到DE=BF，所以四邊形EBFD是平行四邊形。

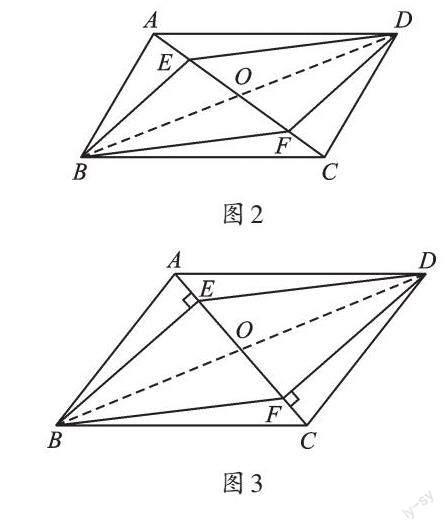
教材中給予的解法是利用“對角線互相平分”的判定定理來證明。其實質是想告訴我們，解決本題，除了“尋找”全等三角形，還可以“構造”全等三角形。如圖2，連接BD，BD交AC于點O，構造出三角形（△BEO、△BFO、△DEO、△DFO），并證明所構造的三角形全等（△BEO≌△DFO、△BFO≌△DEO），進而通過線段和角相等來證明平行四邊形。

變式1 已知：如圖3，在?ABCD中，BE⊥AC，DF⊥AC，垂足分別為E、F。求證：四邊形EBFD是平行四邊形。

【解析】變式1是將原例題中的“AE=CF”變成了“BE⊥AC，DF⊥AC，垂足分別為E、F”。此時，我們只需連接BD，直接證明△BOE≌△DOF，得出對應線段和角的相等關系，從而證明平行四邊形。

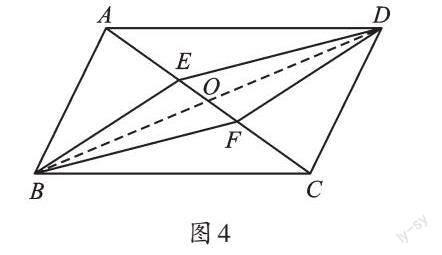
變式2 已知：如圖4，在?ABCD中，∠ABC、∠ADC的平分線分別交對角線AC于點E、F。求證：四邊形EBFD是平行四邊形。

【解析】變式2是將原例題中的“AE=CF”變成了“∠ABC、∠ADC的平分線分別交對角線AC于點E、F”，同變式1一樣，只是條件改變，證明方法類似（連接BD）。……