基于數學三種語言轉化的概念教學

李武

【摘要】在高中數學概念教學中，通過數學三種語言轉化設置實驗操作、強化概念的多元表征、運用具象結合和數形結合策略，激發學生的學習興趣，優化概念的知識結構，培養學生的概念探究能力和構圖能力。

【關鍵詞】數學三種語言轉化；概念多元表征；具象結合

數學概念是人腦對現實對象的數量關系和空間形式的本質特征的一種反映形式，是一種數學的思維形式，是數學之本、解題之源。如果我們在學習的過程中沒有對概念有著深刻的認識，透徹的理解和熟練掌握，那么在數學的學習過程中將會遭遇很多困難，甚至無法進行更深入的學習。但在現實的教學中由于受到應試教育的影響，很多教師把更多的時間放在解題技巧的傳授上，而忽視了數學概念的重要性，認為概念只不過是一個定義，沒有去深究它的內涵。

數學語言不是簡單地描述數學知識，它更是數學思維的一種載體和教學過程的交流工具，數學三種語言包括文字語言、圖形語言和符號語言。在傳統的數學概念教學中通常是教師講，學生被動地接受知識，忽略了學生在課堂教學中的參與性，限制了學生的思維發展和數學核心素養的培養。本文作者將結合自己的教學經歷探討數學三種語言轉化融入數學概念教學中，對概念教學、學生思維培養、學生探究式學習方式及學生數形結合能力的培養都具有現實的教學意義。

一、設置探究操作實驗，培養概念探究能力

隨著課程改革的實施，傳統的數學概念教學模式已經無法滿足新課程標準的需要，所以數學概念課堂教學模式必須要做出轉變。傳統的數學概念教學注重直接從數學概念出發，教學的著重點是教師向學生分析概念的內涵和強調概念滿足的條件和范圍，雖然這樣的概念教學具有嚴謹性，但這種只注重結果的教學使學生沒有真正了解數學概念的本質，阻礙了學生探究知識的過程及思維的過程。可見傳統的數學概念教學模式不適合新課程標準中培養學生數學核心素養的要求，在概念教學中通過數學三種語言轉化設置探究性操作實驗，既培養了學生對概念的探究能力，又實現了概念教學由“知識型”向“過程型”的轉變。

案例一：“橢圓及其標準方程”教學片段。

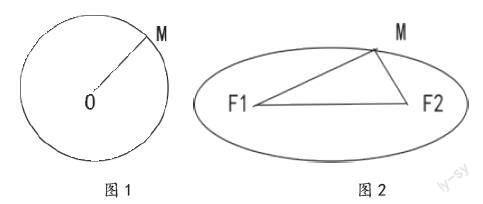
問題1：取一條定長的細繩r，把它的兩端都固定在圖板的同一點F，套上鉛筆，拉緊繩子，移動筆尖，這時筆尖（動點）M畫出的軌跡是 ？

學生：通過文字語言的關系轉化成圖形語言，如圖1。

問題2：觀察上面實驗操作得到的圖形，用集合語言表示動點M的軌跡。

學生：{M||MF|=r}。

問題3：如果把細繩的兩端拉開一段距離2a，分別固定在圖板的兩點F1，F2。套上鉛筆，拉緊繩子，移動筆尖，這時筆尖（動點）M畫出的軌跡是？

學生：通過實驗操作的文字語言轉化成圖形語言，如圖2。

問題4：如何用集合語言表示動點的軌跡。

學生：{M||MF1|+|MF2|=2a>|F1F2|}

問題5：類比于圓方程的步驟—建、設、限、代、化，用方程表示動點M軌跡。

案例一是通過數學三種語言轉化設置探究操作實驗的概念教學，同時將類比推理的數學思想融入其中。案例中就是把數學中對象的相似性作為根據進行聯想，從而將對某一數學對象的已知知識遷移到另一個相似的數學對象上，從而獲得新的發現的思想方法。整個概念的呈現過程通過數學三種語言轉化設置探究性實驗達到教學的目的。概念教學不再是以往的由教師直接給出數學概念的教學模式，而是引導學生通過轉化數學三種語言對問題進行探究的過程，體現了學生是信息的加工主體，整個教學過程讓學生從原來的重“知識型”向“過程型”轉變。案例中通過引導學生類比圓的方程實驗，利用定線和筆尖按照某種定量關系畫出軌跡，并引導學生通過實驗操作觀察如何將圖形語言轉化成符號語言。整個實驗過程不僅體現了引導學生靈活掌握三種數學語言相互轉化的教學理念，同時還體現了類比推理的數學思想。

數學的概念理論性強且抽象，通過三種語言轉化設置探究性實驗操作將新概念與學生原本掌握的概念進行類比，有效幫助學生理解概念、掌握規律，既提高了學生的學習興趣，又降低了學生學習的難度。

二、強化概念多元表征，優化概念知識體系

數學概念的學習過程其實就是學生呈現原有知識再創造的過程。那么要實現學生再創造的方式就是教學由“傳授型”向“探究型”轉變，引導學生親自參與概念的探究過程。在數學概念教學中，通過數學三種語言轉化強化概念的多元表征，有助于學生對概念的掌握和深入學習，優化了數學概念知識結構的系統性，強化數學知識間的練習，進而形成完善的數學概念。

案例二：“全概率”教學片段。

引例1：從標有數字1、2、3、4、5的五張卡片中，依次抽出2張（取后不放回），你能否求出“第二次抽到的卡片是偶數”的概率？

問題1：如何用有序實數描述實驗結果？

學生操作：

（1，2），（1，3），（1，4），（1，5）

（2，1），（2，3），（2，4），（2，5）

（3，1），（3，2），（3，4），（3，5）

（4，1），（4，2），（4，3），（4，5）

問題2：設事件A表示“第一次抽到奇數”，事件B表示“第二次抽到偶數”，用韋恩圖表示事件A、A、B間的關系。

學生操作：

問題3：根據韋恩圖如何用符號語言表示P（B），

學生：從圖形語言轉化成符號語言P（B）=P（AB）+

P（AB）=P（A）P（B|A）+P（A）P（B|A）高中全概率概念具有抽象性，其概念的表征方式也具有多樣性。案例二通過數學三種語言轉化將點集（樹狀法）、圖像（韋恩圖）及公式呈現全概率定義的三種表征達到了教學的目的。在概念教學過程中，引導學生探索全概率的三種表征方式可以讓學生從不同的角度探究和理解全概率的含義，促進學生對全概率有“質”的理解。

三、具象結合，理解概念本質

概念學習的過程就是抽象化的過程，雖然數學概念本身比較抽象，但是數學概念的背景和生成是具體的，如果能在概念教學過程中利用數學三種語言轉化將具體和抽象結合，通過概念探究過程了解概念的本質含義，則有效提高了數學概念的教學質量，達到高效教學的目的。

案例三：“函數的奇偶性”教學片段。

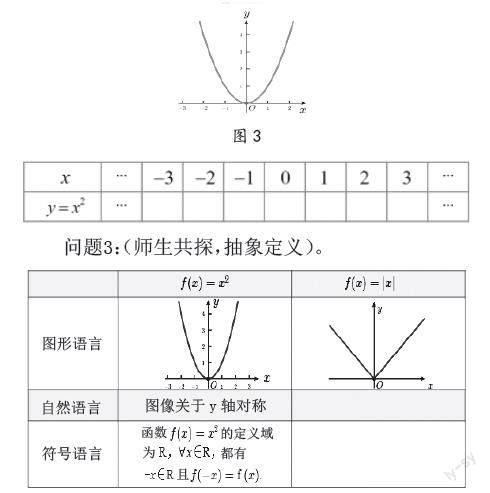
問題1：畫出下列函數（x）=x2，如圖3。

問題2：觀察（x）=x2，填寫函數值對應表。

問題3：（師生共探，抽象定義）。

問題4：（操作體會）請學生上來拖動圖4坐標系中y軸右側的點p，體會對于一個一般函數（x），若其圖像關于y軸對稱，如何用符號語言刻畫？

根據數學概念本身的抽象性和概念生成過程的具體性特點，在概念教學過程中通過數學三種語言轉化設置問題探索，能有效地將抽象概念具體化。案例三中的問題4借助網絡畫板呈現偶函數的圖像特征，引導學生觀察點p的實驗特點，學生很容易從直觀動畫中得到偶函數條件中要滿足的任意性和對稱性，進而準確地用符號語言表示出偶函數的定義，達到概念課堂高效教學的目的。

四、數形結合，培養學生構圖能力

數形結合是重要的數學思想，是學生學好數學必須要掌握的一種方法，在數學概念教學中通過轉化三種數學語言引導學生構圖已成為課堂教學重要的組成部分。在概念教學中，培養學生通過概念的數與形之間的關系去構圖，能有效地將抽象概念具體化、形象化，不僅讓學生更能直觀地理解函數概念，還培養了學生的直觀想象和構圖能力。

案例四：“基本不等式”教學片段。

問題1：請同學們拿出課前準備的四張全等的等腰直角三角形（直角邊用a、b表示，斜邊用c表示，其中a=b），將四個等腰直角三角形擺放成一個正方形，并觀察直角三角形三條邊的關系。

學生構圖：

問題2：請用a、b、c表示出正方形的面積。

學生：S=c2=a2+b2=2b，其中a=b。

問題3：請同學們再拿出課前準備的四張全等的非等腰直角三角形（直角邊用a、b表示，斜邊用c表示，其中a≠b），將四個非等腰直角三角形擺放成一個正方形，并觀察直角三角形三條邊的關系。

學生構圖：

問題4：請用a、b、c表示出正方形ABCD的面積。

學生：

SABCD=c2=a2+b2=2ab+（b-a）2>2ab，其中a≠b。

問題5：綜上分析請同學們大膽猜想并證明a2+b2與2ab之間的關系。

學生：a2+b2≥2ab，當且僅當a=b等號成立。

問題6：以AB是圓的直徑，點C是AB上的一點，設ABa，BC=b過點C作垂直于AB的弦DE，連接AD、BD。

學生構圖：

問題7：請根據圖形建立a，b和CD的關系。

學生：由三角形相似易得CD2=ab，即CD=，∴a+b≥2，其中C與O重合的時候等號成立（當且僅當a=b時取等號）。

數學學習注重的是邏輯思維的轉換，圖形語言就是能將抽象思維向形象思維轉變的載體，而培養學生動態思維關鍵就在于培養學生構圖能力。案例四的整個基本不等式公式的探究是通過數學三種語言的轉化創設問題串引導學生構圖，并通過符號語言表示圖形隱藏的幾何意義，達到概念教學的目的。這樣教學不僅讓學生掌握了所學知識，更重要的是培養了學生的動態思維，符合培養數學建模的核心素養的要求。

【參考文獻】

[1]林青霞.高中生數學概念多元表征的調查研究[D].武漢：華中師范大學，2014.

[2]陸興華，李興貴，堯剛，饒永生.互聯網+動態數學：網絡畫板推進數學教學改革[M].長沙：湖南教育出版社，2018.

（基金項目：本文系海南省教育科學規劃2021年度課題“基于深度學習的高中數學三種語言轉化研究”的研究成果，課題編號：QJH202110070）