層流平板內嵌氯化銀電極模型的電位研究*

嵇 斗 李 琛

（海軍工程大學電氣工程學院 武漢 430033）

1 引言

由于海水具有強烈的腐蝕作用，因此船體的防腐技術是必不可少的，附著在船體表面的電極是陰極保護系統的重要組成部分，通過電位可以定位船體破損的位置，從而避免船體的安全［1］。銀-氯化銀電極屬于第二類可逆電極，又稱為陰離子可逆電極。它是由金屬銀插入氯化銀溶液中所組成的電極。銀-氯化銀電極的特點是：如果難溶鹽是氯化銀，則溶液中就應該含有可溶性的氯化銀。在進行電極反應時，陰離子在界面間進行溶解和沉積（生成難溶鹽）的反應。銀-氯化銀的平衡電位是由氯離子活度和反應溫度來決定的。在銀-氯化銀的電極反應中，進行可逆的氧化還原反應的仍是銀離子而不是氯離子。

國內外學者對氯化銀電極的研究做了大量的貢獻。鄧明等研究了適應海水中的電極材料［2］。苗燕等制備了氯化銀參比電極，并研究了海水流動速度對電極電位的影響［3］。張燕等通過電解法制作了氯化銀參比電極［4］。尹鵬飛等研究了海水相對流動速度對氯化銀參比電極電位穩定性的影響，電位波動在1mV 以內［5］。對于船舶的參比電極，目前大多數采用的是氯化銀參比電極，它具有良好的電位重現性和穩定性，由于它是固體，制作簡單，因此受到了廣泛的應用。氯化銀參比電極的高溫穩定性好，在海水中很難溶解，因此具有良好的防腐蝕性。船體長期在海水中運動，通過流體力學可以研究動海水的特性。流體力學在關于介質流速的求解方面的主要是對層流和湍流兩種流場進行分析。根據文獻［6］可知，關于層流場的理論框架比較完整，并對多種特殊形狀下的流速分布得到了精確解，而流體力學中關于湍流的研究主要基于經驗公式，并沒有形成系統的理論分析，理論分析難度相對較大，最終使理論與實驗結果產生的誤差過大，當前關于湍流場的研究是在經驗公式的基礎上利用數值算法近似進行求解。根據近代流體力學中的流體粘性流動理論及湍流理論可知，當固相金屬放置在流動介質中時，介質會因金屬表面產生的阻力而在距離金屬表面一定范圍內介質的流動狀態呈現近似階梯性分布，該過渡區內介質的流動狀態近似為層流狀態［7～9］。文獻［10～11］應用該理論將復雜物體表面壁的局部等效為平板模型進行了仿真，仿真結果證明該結論的實用性。

本文針對動海水中的外加電流陰極保護系統的氯化銀參比電極電位特性的問題，建立了平板內嵌電極模型，并研究了海水流速與電極電位的關系等影響因素，為動海水中的電極電位特性研究提供了參考。

2 數學模型的建立

由于海水的屬性較為穩定，海水密度很難因外界因素而發生變化，可將其看作不可壓縮流體，海水的粘度一般在0.01N·s/m2～0.02N·s/m2左右［12］。當海水以較快速度運動時，在大部分介質主體流場可以忽略粘度的作用，但在海水與平板接觸表面會因粘度的作用形成薄薄的流體層，在這個薄層內，流體的速度從固壁處的零逐漸增加到相應的無摩擦介質主體的流速，這一薄層流體成為邊界層，介質在其中的流動狀態為層流流動［13］。當固液兩相接觸發生電化學反應時，在固相表面擴散層內會發生物質的傳遞，傳遞時產生的擴散層厚度一般會小于邊界層厚度［14～15］。以水平方向為x方向，平板寬度方向為y方向，建立直角坐標系，電極位于x=1cm處，模型如圖1所示。

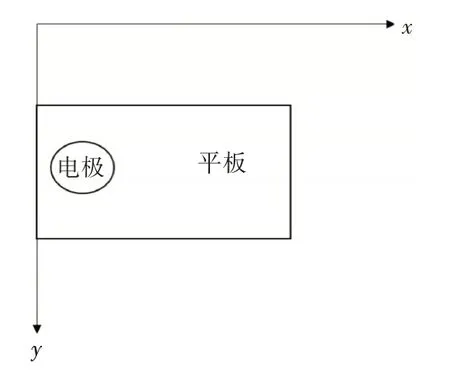
圖1 動海水中的平板內嵌電極模型

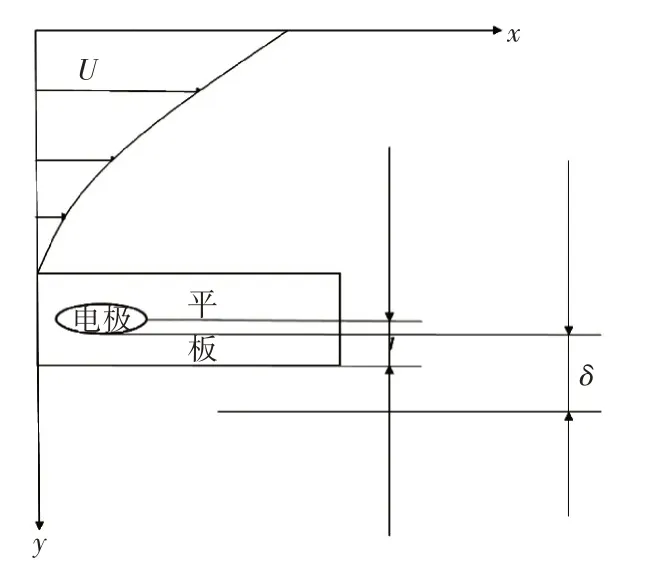
圖2 電極表面海水流速分布

2.1 邊界層方程求解

為了便于做數學分析，可將海水中的流場分成兩個區域進行分析計算：1）平板內嵌電極壁面附近的薄邊界層，必須考慮介質摩擦力；2）邊界層以外的區域，由于該區域摩擦力很小可忽略。

當介質沿平板方向水平流動時，忽略重力的影響而得到的納維斯托克斯方程和連續性方程為

式（1）的邊界條件為

式中：U為平板與海水相對流動速度，cm/s；Vx為x方向上的速度分量，cm/s；Vy為y方向上的速度分量，cm/s；p為海水在電極表面的壓力，N/cm2；ρ為海水的密度，g/cm3；υ為運動粘性系數，cm2/s。

根據數量級比較分析可知：沿邊界層方向（y方向）的速度分量遠小于沿海水流動的方向（x方向），即Vy＜＜Vx，因此Vy可以忽略。由于邊界層的厚度遠小于海水流動的方向所經過的平板厚度，即y＜＜x，同理y可以忽略。化簡得到的普朗特邊界層方程為

由于海水流動速度方向不變，介質濃度分布是均勻的，因此在x方向的壓力梯度可以忽略，即?p/?x=0，由此得到的方程為

為了便于求解，引入流函數Vx=?ψ/?y、Vy=-?ψ/?x代入式（4）整理可得方程

根據相似原理

化簡可得布拉修斯方程為

滿足式（6）的邊界條件為

使用文獻［16］描述的級數展開法求解可設為

代入流函數可得

由文獻［17］可得

由邊界層理論［18］可知：在x方向速度分量Vx=0.99U時的垂直距離y規定為邊界層厚度。

當η=5 時，Vx=0.99U。

在得到流體介質邊界層及平板內嵌電極表面流體速度分量的基礎上，需進一步對平板內嵌電極表面對流擴散傳質過程控制下的電極電位進行求解。

2.2 濃度擴散方程求解

由第一菲克定律可知：若在傳遞過程中物質流入某單位體積的量與流出該體積的物質的量不同時，說明該單位體積內產生了關于該物質的濃度變化。在圖1所示的二維模型中，當通過相距dy的兩個界面通量不相等時，該物質的濃度將隨時間的變化而變化，濃度的變化速度為［19］

式中：D為電極表面銀離子的擴散系數，1.648×10-5cm2/s；c為電極表面的銀離子濃度，mol/L；t為時間常數，s。

由式（11）可知，如果液相中只出現擴散傳質過程，則平板內嵌電極表面的液相傳質過程不可能達到穩態。在保持環境條件不變的情況下，當介質流速分布一定且平板內嵌電極于介質中浸泡一段時間后，平板內嵌電極表面中的銀向介質環境的傳質過程可看做穩態傳質過程。由式（11）可得，處于層流介質邊界層中的穩態對流擴散方程可表示為

當銀在平板內嵌電極表面發生氧化還原反應后的濃度為cs，由于介質主體中的銀濃度遠小于氯，可忽略不計，由此可確定式（12）的邊界條件為

式中：cs為電極表面反應后的銀離子剩余濃度，mol/L。

代入流函數公式可得

將c(x，y)轉化為c(x，ψ)可得式

為了近似求解，取f(η)=0.17η2。

則

代入流函數公式可得

做變換

代入式（17）并化簡可得齊次方程

式（19）為齊次二階微分方程，通過求解可得

通過伽馬函數變換可得

整理可得

式中：c為電極表面位置所在的銀離子濃度，g/cm3；為電極表面銀離子濃度變化率。

3 基于對流擴散作用下的電極表面電位分布

當層流介質中反應物質的傳遞過程達到穩態對流擴散時可得

式中：l為擴散層的厚度，cm。

若控制步驟占主導反應，此時電極的反應速度為擴散速度，擴散速度用電流密度可表示為

式中：n為參與反應的電子數，1；F為法拉第常數，96485.34C/mol；j為電流密度，mA/m2。

在電極表面反應過程中，隨著反應的產生，電流密度越來越大，c逐漸下降。當c降為零時，銀離子的濃度梯度達到最大值，此時的擴散速度最大，電流密度為最大電流密度

式中：jd為最大電流密度，mA/m2。

由于氯化銀是難溶物，根據濃差極化公式可得

式中：Δφ為電極表面電位，mV；R為摩爾氣體常量，8.31J/(mol·K)；T為室內溫度，298K。

4 仿真結果與分析

圖3給出了不同海水相對流速條件下的電極表面銀離子濃度變化率，由圖3可以看出，相對流動速度越大，電極表面銀離子濃度變化率越小，這表明海水中參與反應的主要是氯離子，電極表面參與反應的銀離子與海水中的氯離子結合生成氯化銀，電極表面的銀離子濃度隨著反應的進行越來越小。

圖3 電極表面銀離子濃度變化率與海水相對流速(U)的關系

圖4給出了不同電極位置條件下的海水相對流速變化率，由圖4可以看出，電極表面位置越遠，海水相對流速變化率越小，這表明當海水流經電極表面產生了阻力，在距離電極表面一定范圍內的海水由于其濃度的分布比較均勻，其中的流動狀態可以視為層流狀態，x方向上的速度分量逐漸衰減。當距離足夠遠的時候，x方向上的速度分量變為零。

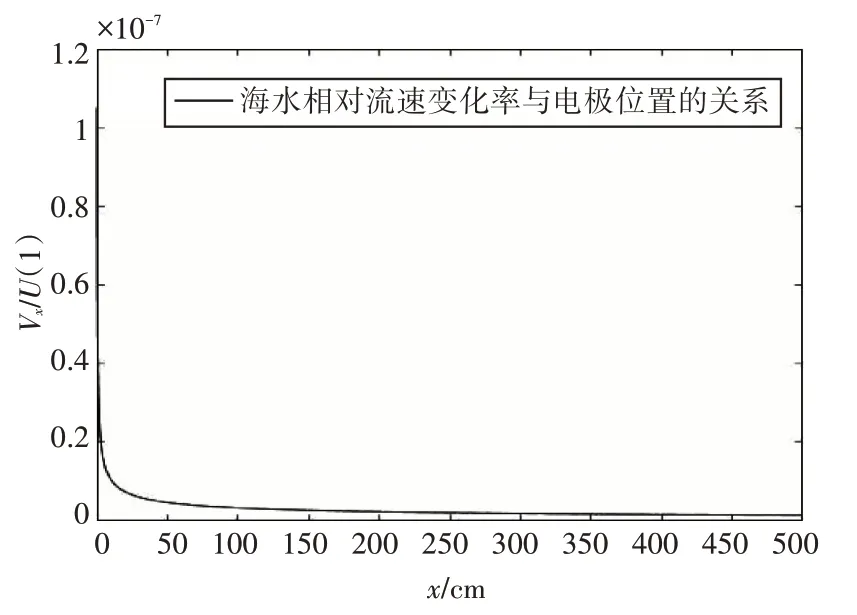
圖4 海水相對流速變化率與電極位置(x)的關系

圖5給出了不同電極位置條件下的電極表面銀離子濃度變化率，由圖5可以看出，電極位置越遠，電極表面銀離子濃度變化率越小，這表明隨著電極表面距離的增加，電極表面參與反應的銀離子所形成的擴散層遠小于電極表面的厚度，電極表面擴散層的銀離子濃度高于外部的濃度，銀離子由濃度高的電極表面向濃度低的海水中擴散，電極表面的濃度越來越低。

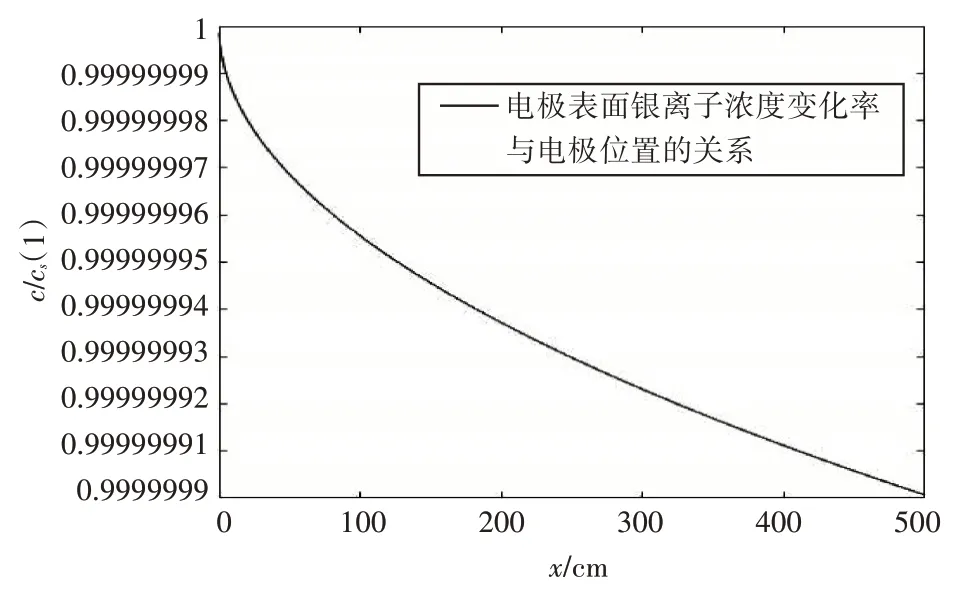
圖5 電極表面銀離子濃度變化率與電極位置(x)的關系

圖6給出了不同海水相對流速條件下的電流密度，由圖6可以看出，海水相對流速越大，電流密度越大，電流方向與相對流速方向相反。這表明電極表面參與反應的銀離子所形成的擴散層受到一定強度的對流影響，電流密度受到電極表面銀離子擴散系數的影響相對減弱了，增加了受對流影響的因素，因此電流密度受到對流與擴散的共同作用。電流密度與運動粘性系數成正比，說明電流密度受到海水的粘性程度的作用。

圖6 電流密度(j)與海水相對流速(U)的關系

圖7給出了不同海水相對流速條件下的電極表面電位，由圖7可以看出，海水相對流動的速度越大，電極表面電位越小。這表明當海水流動時，電極表面的平衡狀態被打破，電極表面的銀離子濃度快速下降，從而使電極表面的電位減小，所以電極電位隨著海水相對流速的增大而減小。

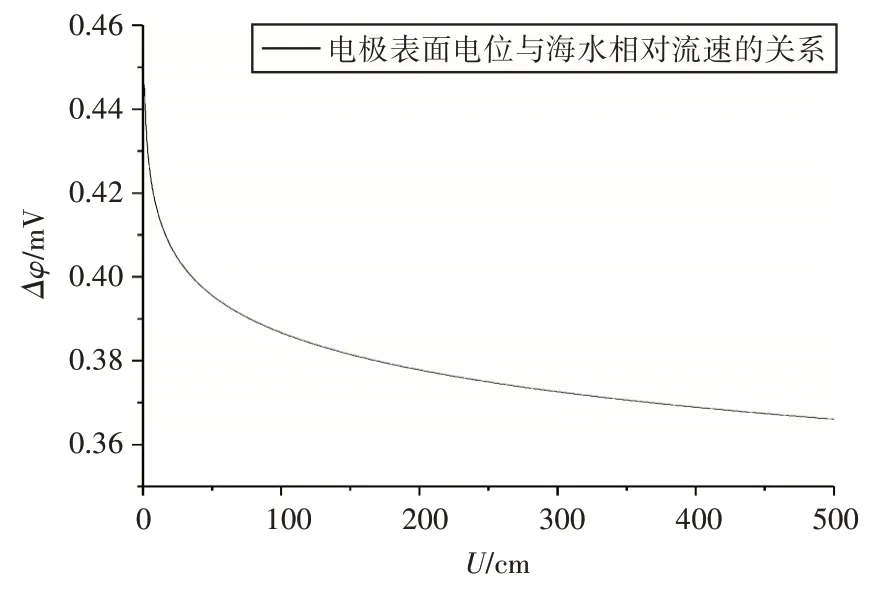
圖7 電極表面電位(Δφ)與海水相對流速(U)的關系

5 結語

本文基于動海水中的陰極保護系統的氯化銀參比電極的電位測量的問題，建立平板內嵌電極模型，研究了電極表面銀離子濃度在動海水中的對流擴散傳質過程，并分析獲得了電極電位的取值范圍。仿真結果表明：海水流速越大，電極表面銀離子濃度變化率越小；電極表面位置越遠，海水相對流速變化率越小；電極表面位置越遠，電極表面銀離子濃度變化率越小；海水流速越大，電流密度越大，電流方向與海水流速方向相反；層流場內海水流速越大，電極表面電位越小。電極電位的取值范圍在0.36mV～0.48mV。