課程思政視域下離散數學課程的教學改革實踐探究

王磊　仇海全　李焱

關鍵詞：離散數學；課程思政；教學改革；CDIO

中圖分類號：G642 文獻標識碼：A

文章編號：1009-3044（2023）10-0154-03

1 引言

2016年12月，習近平總書記在全國高校思想政治工作會議上指出“其他各門課都要守好一段渠、種好責任田，使各類課程與思想政治理論課同向同行，形成協同效應”[1]。高校是人才培養的基地，除了要提升人才的知識和技能水平，更要落實立德樹人的根本任務。

離散數學是計算機相關專業的核心課程，是研究離散量的關系的學科，是計算機科學軟硬件開發的理論基礎。離散數學課程的主要內容包括：命題邏輯、一階邏輯、集合論、二元關系、圖論、組合分析、形式語言與自動機等。通過離散數學的學習，使學生理解離散量的相關理論，掌握各種離散事物的表述方法，培養學生的抽象思維能力與邏輯推理能力。

離散數學一般在大一第二學期或大二第一學期開設，這時期的大學生正處于從高中嚴格管束的應試教育到能夠自主安排學習、逐漸形成自己認知的過渡階段，每天都會接觸形式多樣的媒體，以及這些媒體所帶來的鋪天蓋地的信息與資訊。在這形成人生正確價值取向的關鍵時期，幫助他們在復雜多變的環境中健康成長，樹立正確的“三觀”，養成良好的思維習慣就成為這一階段的重中之重。因此，通過課程思政的引入對離散數學課程教學進行改革探索是必要的，也是必需的。

2 離散數學課程教學現狀

離散數學課程定義多、定理復雜、內容抽象、理解困難，很多高校對該課程教學不斷進行改革與創新，如混合式教學[2]、案例教學[3]、PBL翻轉課堂[4]、課程思政[5]等，以便于學生的學習與把握；然而這些教學方式或方法的改革往往只側重于解決某一方面的問題，不能全面地解決離散數學教學中普遍存在的共性問題。本課程團隊結合多年從事離散數學授課實踐，梳理總結出了教與學中存在的問題。

1）課程內容難度較大。離散數學課程大部分內容枯燥、概念多、知識點繁雜、理論性強且高度抽象，是一門既難學也難教的課程。學生上課過程中提不起興趣，作業不會做。

2）理論與實際相脫節。離散數學是一門理論性很強的課程，教學以理論知識的傳授為主，一般都是采用教師講述的方式進行，課堂上缺乏與學生的互動，忽略了學生的認知感受，學生很難將抽象難懂的教學內容與實際聯系起來，導致學生厭學，課堂上無法集中注意力。

3）缺乏實踐性教學內容。離散數學是計算機相關專業的基礎課程，但是在教學過程中，并未發揮計算機專業的特色，也無法與計算機直接聯系起來，導致對相關理論的理解不夠深入。

4）教師政治素養有待提高。教師在離散數學課程的教學過程中往往只側重對知識點的講解，而對其背景知識、學生的知識儲備與學科素養、課程學習的理論與現實意義等缺乏全面的了解。教師政治素養的欠缺使得教師在講授專業知識的過程中突兀地加入思政課內容而顯得較為生硬、刻意，無法將其自然地融入課堂教學[6]，給人牽強附會之感，與預期的育人目標相去甚遠。

3 課程思政視域下離散數學課程的教學改革探索

3.1 更新教學理念，創新評價機制

“高校教師要堅持教育者先受教育，努力成為先進思想文化的傳播者、黨執政的堅定支持者，更好擔起學生健康成長指導者和引路人的責任”[7]。離散數學教師如何非常自然地在授課過程中將課程思政內容滲透進知識點，對離散數學課程教師來說是一個挑戰，這需要教師具有較高的政治素養和豐富的人文知識。首先，教師要更新教學理念。教師要從思想上認識到課程思政貫穿于離散數學教學全過程的重要性，在傳授知識的同時努力實現育人的目標。教師要站在立德樹人這個角度，而不僅僅只是專業知識傳授者的角度來看待教學。教學過程中應以學生為中心，開發、發現學生的興趣點，結合學生的興趣點有機融入思政元素，點燃學生的學習興趣，引導學生主動學習。為此，教師應具有開展思政教學所必備的知識和技能，注重關注時事政治和科技前沿，將正能量傳遞給學生。其次，建設課程思政團隊，開展定期學習交流。成立課程建設組，定期進行集體備課，研討教學內容，交流新教學模式的實施進程、課程思政的設計思路；課程組的老師要充分發揚“老帶新”的光榮傳統，分享教學經驗，幫助新教師提升教學能力；積極參加相關學術研討會，學習借鑒優秀學校和教師的新理念、新思想、新方法。最后，創新教師教學評價體系。將課程思政納入教師教學評價體系中，通過同行評價、專家評價和學生評價的結果，綜合評估教師課程思政實施效果。目前教師職稱晉升、評獎評優主要考察科研和教學成果，缺乏對教師在立德樹人方面表現的評定，教師為了迎合高校評價制度往往將工作重心放在學科建設和科學研究上，而忽視了教學工作中的“育人”成分。因此，課程思政建設不僅需要教師個人的努力，也需要高校從監督和評價機制上進行創新。

3.2 多維度挖掘課程思政內容

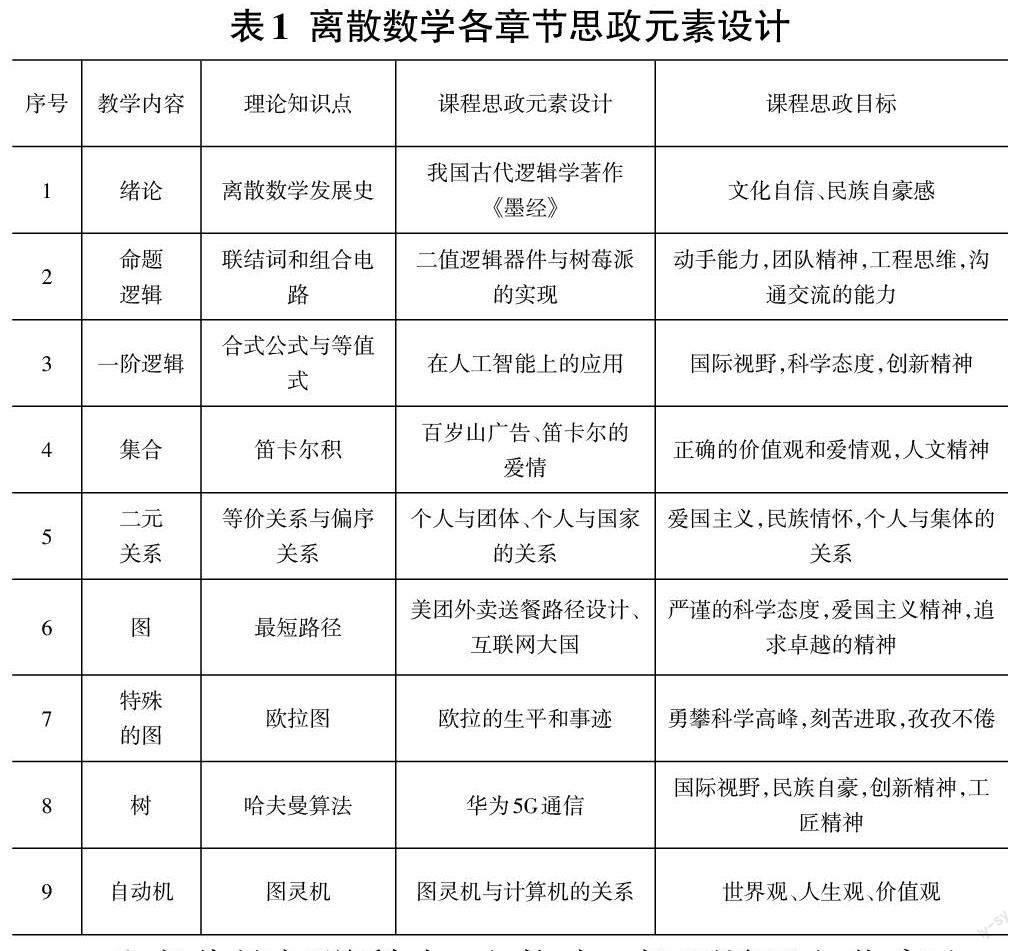
離散數學教學內容主要有：緒論、數理邏輯、集合、圖論等，課程既涉及高等數學、數據庫、數字電路等基礎學科知識，又涉及人工智能、圖像處理、數據挖掘等專業知識，可以發掘出豐富的思政元素。結合學生的專業特點，將教學內容與科學故事、科學前沿、社會熱點、專業知識拓展等相結合，針對每個章節設計恰當的思政案例，提升學生的學習興趣，努力實現立德樹人的目標。每章節的課程思政元素設計如表1 所示。

1）充分挖掘學科史、人物史，實現課程文化育人

數學理論的曲折誕生過程和數學家傳奇的人生經歷可以成為學生的精神榜樣。

例如，德國數學家康托爾創立的集合論起先不被認可，但很快又被大家接受，并得到高度贊譽；然而羅素悖論直接說明集合論存在漏洞，引發第三次數學危機。策梅羅提出的ZF公理系統及馮·諾伊曼等人提出的NBG系統解決了這一悖論。正是這一次次危機推動了數學理論這艘巨輪不斷前進。

通過十八世紀困擾數學界的難題——哥尼斯堡的七橋問題，讓同學們結合圖討論如何求解，引入圖論和一筆畫問題。歐拉在二十多歲時撰寫的《哥尼斯堡的七座橋》論文中解答了這個難題，進而介紹歐拉個人的生平。他將自己的一生奉獻給了熱愛的數學事業，孜孜不倦地撰寫了大量書籍，為后人留下了寶貴財富；同時，開創了數學界的一個新分支——圖論與幾何拓撲。以此鼓勵同學們將更多精力投入學習中，要有為科學獻身的崇高理想。

2）挖掘離散數學知識點中所蘊含的馬克思主義基本原理

為了將思政內容有效融入課程，要深入挖掘離散數學知識點中所蘊含的哲學原理。例如，等值演算中重要的等值式吸收率A?（A?B）?A，左右兩邊是兩個不同的式子，但卻是等值的，啟發學生要透過現象看本質，理解現象背后深層的因果關系，教導學生不要被事物的表象所迷惑。通過范式求解的等值演算法與真值表法的聯系與區別，有向圖、無向圖及帶權圖之間的聯系與區別，引出馬克思主義基本原理中聯系與發展的普遍性原理。闡述任何事物都不是孤立存在的，都與其他事物存在著普遍聯系，通過發現不同知識點之間的相互關系來把握相關知識的本質。通過蘇格拉底三段論無法用命題邏輯證明，而引入一階邏輯來解決，說明科學是不斷向前發展的，要用批判的精神看待事物和問題。在講解形式語言和自動機時介紹深度學習、AlphaGo等相關知識，引出辯證唯物主義的思想與科學探究的倫理道德問題。

3）離散數學在實際生產和生活中的應用

離散數學往往讓學生感覺理論性太強，所學知識與生活現實嚴重脫節，為此，在教學過程中引入具體案例介紹離散數學在實際中的應用就顯得很有必要。例如，通過介紹計算機發展的歷程以及目前計算機領域的研究方向，來引入說明作為基礎學科的數學的重要性。軟件產業的發展要依靠雄厚的數學知識作為基礎和后盾。雖然華為的第五代移動通信技術成為世界通信領域的行業標桿，但我國信息技術的數學基礎仍然較為薄弱，導致軟件產業的發展受阻；另外，算法分析、信息壓縮、網絡安全、大數據等行業和領域也都迫切需要扎實的數學基礎作為依仗。既要讓學生認識到我國改革開放以來飛速發展取得的不凡成就，同時也要讓他們認識到我們與外國尤其是發達國家的差距，特別是在基礎學科和高科技等領域的差距。可以在講解第六章時介紹如何通過加權圖尋找城市交通最短路徑，講解第七章時突出說明二部圖被廣泛應用在目前主流的推薦算法上是時下熱門的研究方向之一等實際應用案例，來激發學生的好奇心和求知欲。

3.3 基于CDIO 工程項目實施模式的實踐課，提高工程實踐能力

離散數學知識應用廣泛，很多復雜問題可以借助于離散數學知識來解決。離散數學與數學、計算機聯系緊密，可以利用專業優勢，建立離散數學模型，設計算法，將各學科知識融會貫通。教師在實驗案例的選擇和設計時應注意將驗證性實驗與創新性實驗并重。驗證性實驗主要是通過編寫程序對離散數學的概念和定理進行驗證，加深理解。創新性實驗具有較高的難度，例如，基于主析取范式和主合取范式對案件進行推理、基于二部圖的推薦算法等。實驗過程采用CDIO工程項目實施模式[8]，項目組同學共同完成某個任務。按照周期，規劃每個階段的任務，對任務進行分解，再開展方案設計，通過分工和分步驟開展實施，最后測試并總結。這有助于提高學生團隊合作和解決復雜問題的綜合能力。

3.4 立體化考核方式

為了更加科學地檢驗學生的學習效果，采用立體化考核方法，平時成績占比20%、實踐能力考核占比20%、終結性考核占比60%。平時成績包括出勤、隨堂測驗、課堂參與度、主題發言等。主題發言主要是考查學生的文獻閱讀，資料收集、整理，團隊合作等方面能力，要求學生自行分組，以團隊的形式準備發言內容，發言主題由教師結合教學內容指定或者學生自擬。實踐能力考核以往采用學生的實驗報告作為評分依據，但現實中存在實驗報告抄襲嚴重現象，無法反映學生的真實水平。為此，在CDIO項目實踐過程中，通過記錄學生實踐的階段性表現，結合任務完成的效果進行打分，打分合格的同學取得相應的實踐考核分數。立體化考核方式能夠全過程記錄學生的整體表現，能夠做到相對更加公平、公正。

4 教學成效

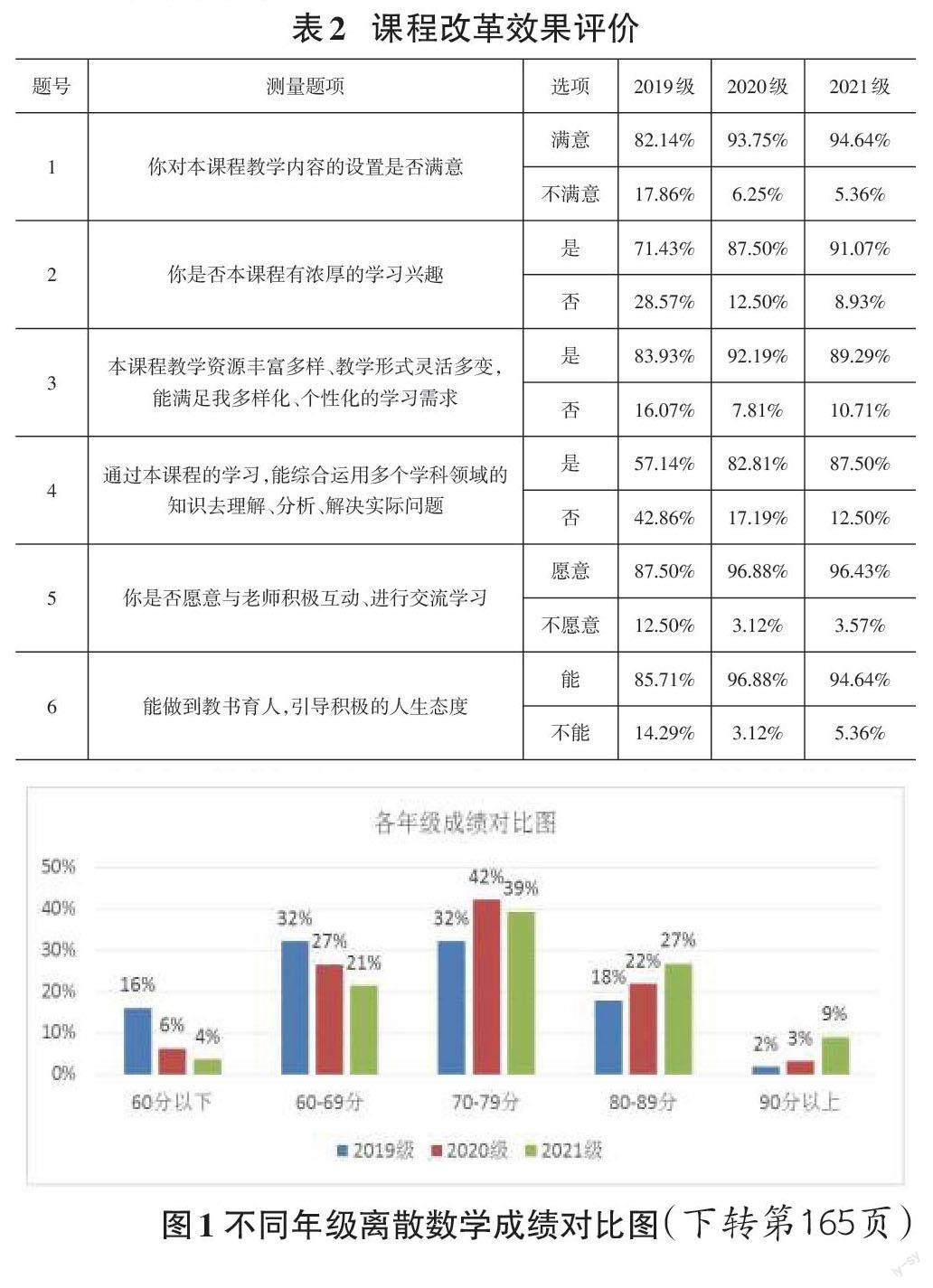
基于傳統教學模式存在的問題，我校信息與網絡工程學院計算機科學與技術專業自2021年開始對離散數學實行課程思政教學改革，表2中2019級學生仍然采用傳統教學模式授課，為了解離散數學課程思政改革成效，對近三年計算機科學與技術專業學生開展滿意度調查，調查問卷采用的是問卷星線上調查的方式，調查對象是2019級（56人）、2020級（64人）和2021 級（56人）計算機科學與技術專業學生共計176人，最終回收問卷176份。調查樣本符合調查分析的技術要求。問卷中的問題均采用選擇題的形式，每題均有兩個選項。調查結果如表2所示。開設了課程思政教學改革后的班級對教學內容的設置滿意度提高，激發了學生學習興趣，學生普遍認為理論能夠聯系實際，能夠解決實際問題，愿意積極主動與老師交流，能夠做到“教書育人”。

由圖1數據可見，2020級和2021級實施教學改革后的成績有明顯提高。

5 結束語

課程思政是培養大學生德才兼備的重要手段。在離散數學課程中融入課程思政，是落實國家人才發展戰略和全面育人的現實需求。通過在課程教學過程中滲透思政內容，充分挖掘學科歷史；在教學案例中設計思政元素，將離散數學的知識應用到實際生產生活中去；設計實踐課案例，采用CDIO項目模式開展，培養學生團隊協作精神；立體化考核方式能更好地反映學生學習情況，從而達到激發學生學習積極性，提升人才培養質量的目的。