基于PNN模型和RF模型的瀝青路面使用性能預測研究

趙國武、劉濤、金磊、董磊、楊紀舉

（1.臨沂市公路事業發展中心，山東臨沂 276007；2.山東通維信息工程有限公司，山東濟南 250000；3.臨沂市公路事業發展中心郯城縣中心，山東臨沂 276037）

0 引言

近些年，隨著車輛保有量持續增長，路面行車荷載也隨之急速增長，隨之帶來了瀝青路面使用壽命減少、使用性能下降的后果。及時科學預測并評價瀝青路面使用性能狀態，是實現制定養護策略、保障瀝青路面使用和服務性能的關鍵[1]。目前，針對路面使用性能的評價多依賴于相關規范，未能充分挖掘路面性能使用指數和其他指數之間的關系。現有的研究多通過多項式回歸的方法獲取路面性能使用指數的表征方式[2]。除此以外，相關權重系數僅通過道路等級確定，而非根據道路實際使用情況確定，如此將導致所得到的路面性能指數預測公式與實際數據貼合不緊密，魯棒性與泛化性能不強，無法較好地應用于實際當中[3]。因此尋求一種貼合于道路實際使用情況的性能評價方法極為重要[4]。

為了解決上述問題，諸多學者做出了很多努力。張凱星等[5]以廣東省的道路數據為研究對象，通過采用BP 神經網絡，將路面結構強度納入路面使用性能考量因素中，最終結果證明，通過此種方法可以在一定程度上對路面使用性能進行評價。張麗娟等[6]同樣以廣東省瀝青路面相關數據為研究對象，基于ARIMA 和支持向量機（SVM）算法構建瀝青路面PCI 的預測模型，試驗結果表明，此兩種方法可以較好地對瀝青路面使用性能進行預測。孫鵬等[7]則是通過采用灰色預測模型，實現對瀝青路面使用性能指數PQI 的預測。相似的是，商博明等[8]以市政道路路面為研究對象，通過灰色馬爾可夫模型實現了對路面使用性能較為準確的預測。總的來說，現在大多數瀝青路面使用性能預測多基于數學統計模型（層析分析法、灰色預測、粒子群算法等）以及機器學習模型（SVM、BPNN等），但是大多數研究僅是研究一種算法在路面使用性能預測上的表現如何，缺乏對多種算法對同一路面數據的橫向對比研究。

綜上所述，本文以臨沂市瀝青路面數據為研究對象，基于概率神經網絡（Probabilistic Neural Network，PNN）和隨機森林（Random Forest，RF）構建瀝青路面使用性能評價指數預測模型，并以整體預測準確率和子類別預測準確率為評價指標進行對比分析，以得到預測準確率較高的模型來解決瀝青路面使用性能指數PQI 的預測問題。

1 PNN 模型和RF 模型預測原理

1.1 PNN 模型基本原理

概率神經網絡（PNN）模型是一種較為有效的預測神經網絡模型，屬于前饋神經網絡，是徑向基網絡的一種變體。從本質上說，此種網絡是一種自監督網絡，需要特定的標簽進行學習識別。相較于多層感知機，PNN 運行速度更快、準確度更高，更為重要的是對于異常值的敏感性更低。總體而言，PNN 由四部分組成，即輸入層（Input），模式層（Pattern Layer），求和層（Summation Layer）以及輸出層（Output）。PNN的結構如圖1所示。輸入層用于將所需要學習認知的數據傳入網絡，模式層則用于計算所輸入數據的特征向量與其各自模式的匹配程度，即相似度。值得一提的是，模式層的神經元個數是和輸入的數據樣本個數保持一致的。

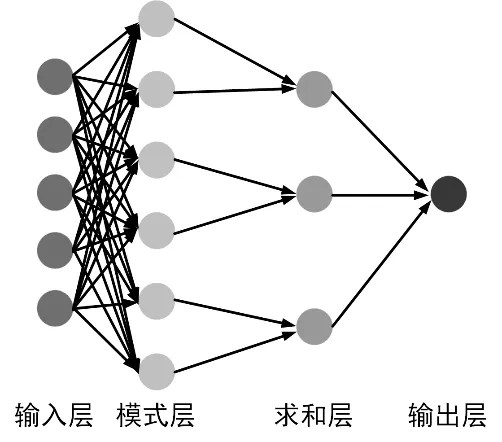
圖1 PNN 的結構圖

從上述描述及圖1 可知，輸入層和模式層之間通過某個高斯函數相連接，通過計算模式層和輸入層中各個神經元之間的匹配程度并進行累加求和平均數學運算，最后可以預測出輸入數據的所屬類別。則PNN 的數學計算表達式可用式（1）進行表示

式（1）中：yg表示網絡的輸出值；lg表示g 類的數量；表示g 類的第i 個神經元的第j 個數據。

1.2 RF 模型基本原理

隨機森林（RF）算法，屬于集成學習中的Bagging（也稱為Bootstrap Aggregation）的方法。RF 是基于決策樹而形成的一種有監督學習算法。決策樹通過樹形結構，利用層層推理的方式學習輸入數據的關鍵特征，進而實現對關鍵類別的分類學習。從本質上來講，決策樹是一種基于if-then-else 規則的有監督學習算法。隨機森林算法就是基于眾多無關聯的決策樹，實現對數據的分類學習。具體來講，隨機森林即是通過組合多種分類器，以投票的方式結合多個分類器的預測結果，進而提升整體算法的預測魯棒性。總體來說，RF 的數據處理預測主要可以分為三個部分，其運行流程如圖2所示。

圖2 RF 運算示意圖

在RF 算法計算過程中，獲得一個可靠的預測結果的關鍵是選取典型的關鍵特征。其中，基尼系數是特征選擇的關鍵，基尼系數計算方法如式（2）所示。

式（2）中：p表示概率值；K表示某一類別。

2 PNN 模型和RF 模型預測PQI 值對比

2.1 PNN 模型和RF 模型預測PQI 值

本文以臨沂市2021年瀝青路面使用性能檢測數據為研究對象，進行兩種預測模型基于行駛質量指數（RQI）、路面狀況指數（PCI）、路面車轍深度指數（RDI）、磨耗指數（PWI）以及跳車指數（PBI）5 種路面特征指數對路面使用性能指數（PQI）的預測準確率進行對比研究。現對上述指數進行介紹。行駛質量指數RQI：該指數主要用來反映路面的憑證情況，一般而言，路面的平整度會受到荷載、道路結構、路面材料、外界環境等多種因素影響，之間的影響關系較為復雜。通過一些車載傳感器設備可以獲取路面平整度信息。路面狀況指數PCI：用來反映道路在服役過程中的損壞情況。總體上來說，道路損壞可以分為兩種，即外部損壞和內部損壞。該指數主要用來反映路面外部損壞程度。其量化方式主要通過車載攝像機拍攝路面情況，對圖中路面損壞情況進行分類統計并量化。車轍深度指數RDI：用來衡量路面在車輛反復荷載下的沉陷深度，是衡量路面舒適程度的重要指標。磨耗指數PWI：該指標主要用于反映路面的整體粗糙程度，可以對瀝青路面的表觀構造微觀特征進行描述。該指標反映了路面的摩擦阻力、降噪能力等特性。跳車指數PBI：該指標從某種程度上反映了路面在服役過程中縱斷面的變化情況。

本文基于上述路面評價指標，通過實際數據構建路面性能綜合評價指標的表達式。選取了臨沂市2021年的數據進行處理并構建。初始得到的數據共有2140 條，通過刪除缺損、異常的數據，最終可用的數據共有1220 條。基于PQI 數值大小（0～100）將其分為4 個類別，即優、良、中、次，分別記為4、3、2、1。通過統計可以得出，各個類別下的數據各有847、314、56、3 個樣本。由于PQI 類別為1 的樣本數據過少，在使用模型進行分析預測的過程中，此類別無法充分學習其特征并得到準確可靠的預測結果，故本文將PQI類別為1 和2 的樣本數據合并，統一定為2。

通過基于本文1.1 和1.2 小節所述的PNN 和RF模型基本原理，基于Scikit-Learn 第三方庫，用Python 編程語言實現上述計算過程，最后所得的兩種預測模型結果如表1所示。

表1 RNN 和RF 模型對PQI 的預測準確率比較（2021年數據）

從表1 結果可以得出，RF 模型在整體預測準確率上遠高于PNN 模型，其準確率高達99.67%。除此以外，兩種模型針對類別4 樣本，即PQI 指數為優秀的類別樣本，預測準確率均達到了100%。而對于類別3 和類別2 的樣本數據（即PQI 指數為良和中）來說，PNN無法正確預測該兩種類別的樣本數據，反觀RF 模型可以較為準確地進行預測，其準確率分別為98.61%和100%。

造成這種現象的原因可能是，在測試集中的類別2 和類別3 樣本數據過少，無法滿足PNN 模型對這兩種類別樣本數據的特征學習，進而不能進行較為準確的預測。另外，從這個結果還可以得到，RF 模型在小樣本數據上的敏感性要遠低于PNN 模型。

2.2 模型對比及實際應用

為了進一步對比驗證PNN 模型和RF 模型在PQI指數驗證上的預測魯棒性和模型泛化性能，本文隨機選取了臨沂市2019年共計200 組PQI 指數相關數據。使用上述基于2021年訓練測試得到的相關模型，在此200 組數據上進行預測。各類別及整體準確率如表2所示。

表2 RNN 和RF 模型對PQI 的預測準確率比較（2019年數據）

從表2 中不難看出，RF 模型在整體準確率上依舊優于PNN 模型。兩種模型在類別4 樣本上均表現出較高的準確率，而在類別3 和類別2 樣本數據上，兩種模型表現依舊相同。從上述結果可以得出，PNN 模型和RF 模型在本測試集上具有較好的魯棒性和泛化性能。

3 結論

本文以臨沂市瀝青路面使用性能相關數據為研究對象，通過PNN 模型和RF 模型分別進行了瀝青路面使用性能指數（PQI）預測對比研究，從中得出以下結論：第一，RF 模型相較PNN 模型具有較強的預測能力，整體預測準確率及單個類別預測準確率均較高；第二，RF 模型和PNN 模型均具有較好的魯棒性和泛化性能，對數據的敏感性較小；第三，PNN 模型相較RF 模型而言具有較強的樣本數量敏感性，易因樣本數據量多少影響其預測準確率。在之后的研究中，將收集更多數據，使所建立的預測模型可以充分學習獲取PQI 指數特征信息。