超聲速飛行器近場聲爆信號反演技術

馬 創，黃江濤，*，劉 剛，陳 憲，舒博文，，陳其盛，高正紅

(1.中國空氣動力研究與發展中心，綿陽 621000；2.西北工業大學 航空學院，西安 710072)

0 引 言

聲爆是超聲速飛機飛行中特有的氣動聲學現象[1-2]。飛行器在超聲速飛行時，其近場產生復雜的激波-膨脹波波系，這些波系傳遞到地面，形成空間內N形的聲壓分布[3]，這就是聲爆現象。聲爆現象會對生物體和建筑物產生不良影響，因此早期的超聲速客機只能在海洋上空進行超聲速飛行。20世紀中后期，英法和蘇聯研制的以“協和”號和“圖-144”為代表的第一代超聲速客機都因聲爆過強而被許多國家禁止在境內飛行[4]，嚴重影響了其商業運營，最終以失敗告終。聲爆評估與抑制是超聲速民機發展必須解決的卡脖子問題[5]。

聲爆抑制涉及空氣動力學與聲學等多個學科，目前主要途徑有流動控制（靜音錐[5]、熱流注入[6]、矢量發動機[7]等）、新概念低聲爆布局（雙向飛翼[8-9]布局、可變前掠翼布局[10]、雙翼布局[11]等）、氣動外形優化（代理優化[12-14]、梯度優化[15-17]、進化算法[18]等）……研究表明，在各類方法中，飛機氣動外形設計是聲爆抑制的最有效途徑之一。其中，通過等效面積分布（equivalent area, EA）指導氣動外形優化[19]是開展低聲爆氣動優化設計的一項關鍵技術。

等效面積分布是沿機身軸線的體積截面積分布與升力分布的疊加，直接決定了超聲速飛行器的聲爆特性，而飛行器等效面積分布特征較大程度由近場過壓決定[20]。但是，通過近場過壓反設計抑制遠場聲爆，缺乏直接的遠場感知聲壓級作為指導。因此，探索有效的遠場聲爆信號向近場過壓反演方法是開展聲爆抑制研究的關鍵環節。

傳統的低聲爆反設計主要基于JSGD（Jones-Seebass-George-Darden）方法開展。20世紀70年代末，Jones、Seebass、George、Darden 四人[21-26]首次提出基于超聲速線化理論的JSGD方法，為低聲爆反設計奠定了理論基礎。該方法在NASA的高速民用運輸計劃（high speed civil transport, HSCT）中得到廣泛應用[27]。國內馮曉強等使用聲爆預測算法與遺傳算法對JSGD參數進行了優化[28]。但JSGD方法存在試湊的問題，且基于線化理論，對于復雜構型的計算誤差較大，屬于反向等效面積分布設計方法[29]。因此，有必要探索一種正向等效面積分布設計方法。

本文擬對近場聲爆信號反演方法的“逆向傳播+POD（proper orthogonal decomposition）”和“逆向傳播+伴隨方程”兩種實現途徑開展研究，以期為等效面積分布指導的超聲速低聲爆飛行器氣動優化設計提供技術支持。

1 聲爆信號的逆向傳播

以零為初始值開始近場信號反演，無論是POD反演方法還是伴隨方程反演方法，都將導致龐大的計算量，尤其對于POD方法，所需的樣本空間極大。因此獲取可靠的初始波形是進一步準確反演的關鍵。

遠場聲爆信號的逆向傳播可以得到近場聲爆信號大致波形，為進一步細節反演提供有力技術支撐。

1.1 聲信號逆向傳播模型

本文通過逆向增廣Burgers方程來建立聲爆信號的逆向傳播模型。推導過程如下。

經典增廣Burgers方程的無量綱形式為：

等號右端項依次對應聲信號在大氣中傳播的非線性效應、經典耗散、非均勻介質和分子弛豫現象。式中：τ為無量綱時間，參考時間為1 / ω0，由近場聲爆信號的采樣頻率決定；Γ為無量綱氣體耗散系數； θv為無量綱分子松弛時間；Cv為無量綱松弛系數。

在經典增廣Burgers方程中，幾何擴散項和大氣分層項取決于聲管傳播路徑與面積，與時間相關的項只有非線性效應項、經典耗散項和分子弛豫項。建立逆向Burgers方程即對這幾項進行修改，令時間反向流動[30]。

描述聲信號逆向傳播的逆向增廣Burgers方程為：

1.2 逆向增廣Burgers方程求解

逆向增廣Burgers方程數值求解時，對過壓信號進行時間離散，對聲管傳播路徑進行空間離散，并對相關參量進行無量綱化處理。使用算子分裂法[31]對式（2）進行求解，可分裂成以下五項：

求解過程中，在當前高度依次更新無量綱壓力P，空間推進直至目標高度，完成求解[32]。

式（3）可整理為如下形式：

式（9）～式（11）給出了式（8）的離散方法：

式（4）經典耗散項和式（5）分子弛豫項均為病態方程。為穩定求解，引入偽拋物線型正則化方法進行修正，修正形式如下：

依照工程經驗選擇 ε =1×10-4。引入式（12）所示的偽拋物型方程改寫經典耗散項和分子弛豫項。

經典耗散項可以寫成：

分子弛豫項可以寫成：

其中，α取0.5。

改寫后的經典耗散項和分子弛豫項均為三對角方程。使用TDMA方法[33]進行求解。

式（6）和式（7）為守恒方程，求解方法如下：

2 基于POD理論的聲爆信號細節反演

由于正向傳播與逆向傳播均存在一定耗散，導致逆向傳播結果中局部激波信號丟失，需要進一步對聲爆信號進行精細化反演計算，以盡可能還原真實波形的細節。

本征正交分解是一種基于快照來描述高維空間的方法，其衍生的Gappy POD方法可進一步修復此高維空間內的任一殘缺快照，因而可以用于反演近場聲爆信號細節。

將設計好的目標遠場波形作為殘缺快照中的已知部分，待求的近場聲爆信號作為殘缺快照中的未知部分，通過對殘缺快照的修復來實現對遠場聲爆信號的反演。

2.1 本征正交分解（POD）方法

POD本質上是一種降維方法。對于近遠場樣本組成的快照集 {Yi，i=(1,2,···,N)}(Yi∈Rn)，POD可以從中尋找主要模態作為基模態使所有快照在各階基模態組成的子空間上正交投影最大，表達式為：

然后，計算快照的脈動矩陣P：

采用奇異值分解（singular value decomposition, SVD）方法進行特征值分解。奇異值分解計算效率高于傳統特征值分解方法，且在計算高階模態時更精確。對矩陣P進行奇異值分解可得：

其中：U∈RN×N，V∈RN×N。 Λ ∈RN×n且僅有對角線元素Λii= σi(σ1≥ σ2≥ ···≥ σr≥0)非零，并得到各階模態：

任意一個快照（如第i個）都可以由各階模態的線性疊加得到，

定義各模態的能量為其對應的奇異值平方，

按照能量原則來選取基模態，定義能量下限為99.9%，即滿足式（27）的前p階模態被選擇作為基模態。

2.2 Gappy POD方法

對于一個殘缺樣本，在POD的基礎上發展出的Gappy POD方法可對其進行修復。對于一個如下形式的殘缺樣本

其中：K為樣本中的已知元素，在本文中為遠場聲爆信號值；U為樣本中的未知元素，在本文中為待求的相應近場聲爆信號值。

POD方法提取出前p階模態作為主模態，按以下形式給出：

基于最小二乘法，使用主模態對殘缺樣本中的殘缺部分進行修復：

其中， Γ =(γ1,γ2···γL)T為殘缺樣本I在主模態張成的新的p維空間中的坐標。

修復得到的殘缺樣本中的缺失數據為：

2.3 聲爆信號的“逆向傳播+POD”反演方法

前文對POD理論的介紹也表明POD方法對樣本空間的依賴性。由于超聲速飛行器近場激波-膨脹波波系的存在，近場聲爆信號波形大多呈現“N”形起伏。直接使用POD方法進行反演，對主模態的要求過于嚴苛，難以得到理想結果。

本文提出了逆向傳播與POD結合的反演方法。首先進行聲爆信號的逆向傳播，得到近場聲爆信號的波形主特征。以此為初始值進行POD計算，大大減少了POD的計算成本，僅需構造波形細節所需的樣本空間，再對逆向傳播的近場波形進行擾動取樣即可。

采用“擾動取樣—POD”迭代計算的方法進行反演，盡可能準確地還原聲爆信號的局部激波。

3 基于伴隨方程的聲爆信號細節反演

基于聲爆伴隨方程求解梯度信息與差分方法相比，避免了大量重復進行Burgers方程求解的正計算過程，是一種高效的梯度求解方法，可基于逆向傳播結果反演聲爆信號細節。

將目標遠場聲爆信號視為目標函數，近場過壓信號的每個時間離散點對應的過壓值作為設計變量，以逆向傳播得到的近場聲爆信號為初始值進行梯度尋優，以得到更精細化的反演結果。

3.1 聲爆伴隨方程推導與梯度求解

將增廣Burgers方程式（1）進行算子分裂后寫成矩陣形式：

式（32）～式（35）分別對應氧氣分子（O2）弛豫效應、氮氣分子（N2）弛豫效應、經典耗散、非線性扭曲這四個聲爆信號傳播的物理環節。kn為增廣Burgers方程式（1）右端第四項與第五項的乘積，表征幾何擴散和大氣分層對聲爆信號幅值的影響。P、q、r、t分別表示求解過程中聲壓的四個中間值。

由上述矩陣形式，構造式（36）所示的拉格朗日量，推導聲爆伴隨方程的矩陣形式。

其中：l為目標函數；N為垂直空間網格數；D表示設計變量，即每個時間離散點對應的過壓值； γ0、 γ1、β、λ分別為式（32）～式（35）表示的四個物理環節對應的伴隨變量。

式（36）使用鏈式求導法則對設計變量D求導，可得：

令所有狀態變量對設計變量的全導數為0，可以得到聲爆伴隨方程。

式（39）為聲爆伴隨方程，可進行迭代求解。將迭代結果代入式（38），可求得目標遠場聲爆信號對當前近場聲爆信號設計變量的梯度信息。

3.2 聲爆信號的“逆向傳播+伴隨方程”反演方法

絕大多數氣動設計問題都可抽象為優化問題。本文的對聲爆信號反演的研究，可視為如下所示的單變量最優化問題：

其中：Ftarget為目標遠場過壓信號；Ni為當前近場過壓信號，以逆向傳播所得的過壓信號為初始值；FNi為 相應的遠場過壓信號；EM為歐氏距離；Ii為優化目標函數，只與當前一輪正計算的遠場聲爆信號有關。

通過求解聲爆伴隨方程更新目標函數對設計變量的梯度信息，基于序列二次規劃算法進行梯度尋優，可得近場過壓信號的反演結果。

4 基于LM1021標模的聲爆信號反演技術驗證

采用第二屆聲爆會議SBPW（the second sonic boom prediction workshop）提供的LM1021標模算例[34]對提出的方法進行可信度驗證。LM1021外形示意于圖1。

4.1 近場聲爆信號與遠場預測

在飛行器流場中，機身周向角0°的近場區域提取壓力值，并計算得到過壓值。近場過壓信號在空間內的分布如圖2所示。

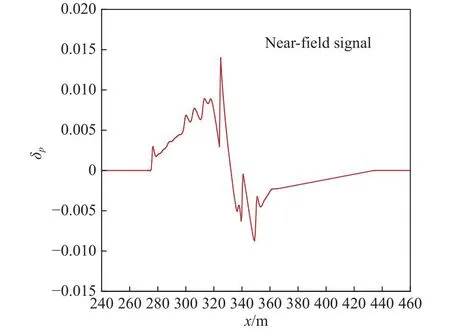
圖2 近場聲爆信號參考值Fig.2 Reference of near-field sonic boom signal

圖3給出了聲爆預測程序得到的遠場聲爆信號預測結果。由于預測程序中進行了時空變換，遠場聲爆信號為地面某一空間位置固定的觀測點處的壓力值隨時間的變化。

圖3 遠場聲爆信號參考值Fig.3 Reference of far-field sonic boom signal

本文提出的反演方法是對圖3所示的遠場聲爆信號進行反演計算，使反演結果具有與圖2所示的近場聲爆信號等效的可信度。

4.2 遠場聲爆信號的逆向傳播

基于逆向增廣Burgers方程求解波形B的逆向傳播結果，目標高度為飛行高度H= 16 747 m，聲爆信號時間離散點數 ω0=50000。為了減少離散格式的數值耗散，垂直方向網格數為 5 0000。正則化參數ξ=1×10-6。

圖4給出了逆向傳播結果與真實近場過壓分布的對比。經過逆向傳播得到的波形，較為準確地反映了真實近場過壓分布的主要特征。從圖5中可以看出，僅經過逆向傳播計算，近場聲爆信號仍然存在較大誤差，精度未達到設計要求。逆向傳播誤差較大部分主要由病態方程正則化造成，需要進一步對聲爆反演信號進行精細化計算，以還原被耗散掉的細節。

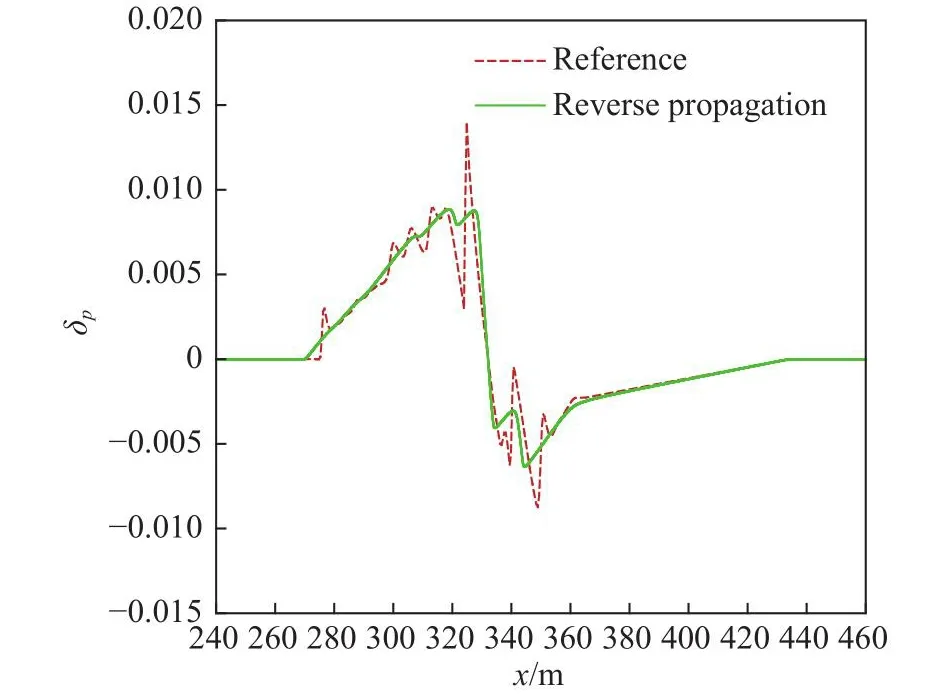
圖4 逆向傳播結果Fig.4 Result of reverse propagation

圖5 逆向傳播結果相應的遠場聲爆信號Fig.5 Far-field wave corresponding to near-field wave of reverse propagation

4.3 聲爆信號細節反演

聲爆信號的細節反演采用兩種方案，分別為POD反演方法與伴隨方程反演方法，均以逆向傳播的結果為初始值進行。

4.3.1 基于POD方法的聲爆信號細節反演

首先將逆向傳播得到的近場過壓信號參數化，以定義設計域和控制變量。精細化反演計算的設計域為強激波區域，基于三次非均勻有理B樣條（non uniform rational B-spline, NURBS）將設計域參數化，定義設計變量共80個，如圖6所示。

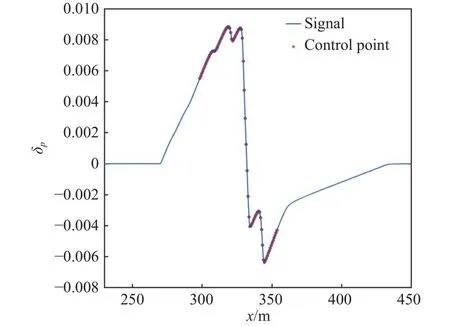
圖6 設計域與控制點分布Fig.6 Design area and control points distribution

逐個擾動控制變量，擾動量為 ± 0.001，擾動生成的每個近場樣本都通過增廣Burgers方程預測其對應的遠場波形樣本。一對相應的近、遠場聲爆信號樣本組成完整的快照。圖7給出了擾動生成的快照集。

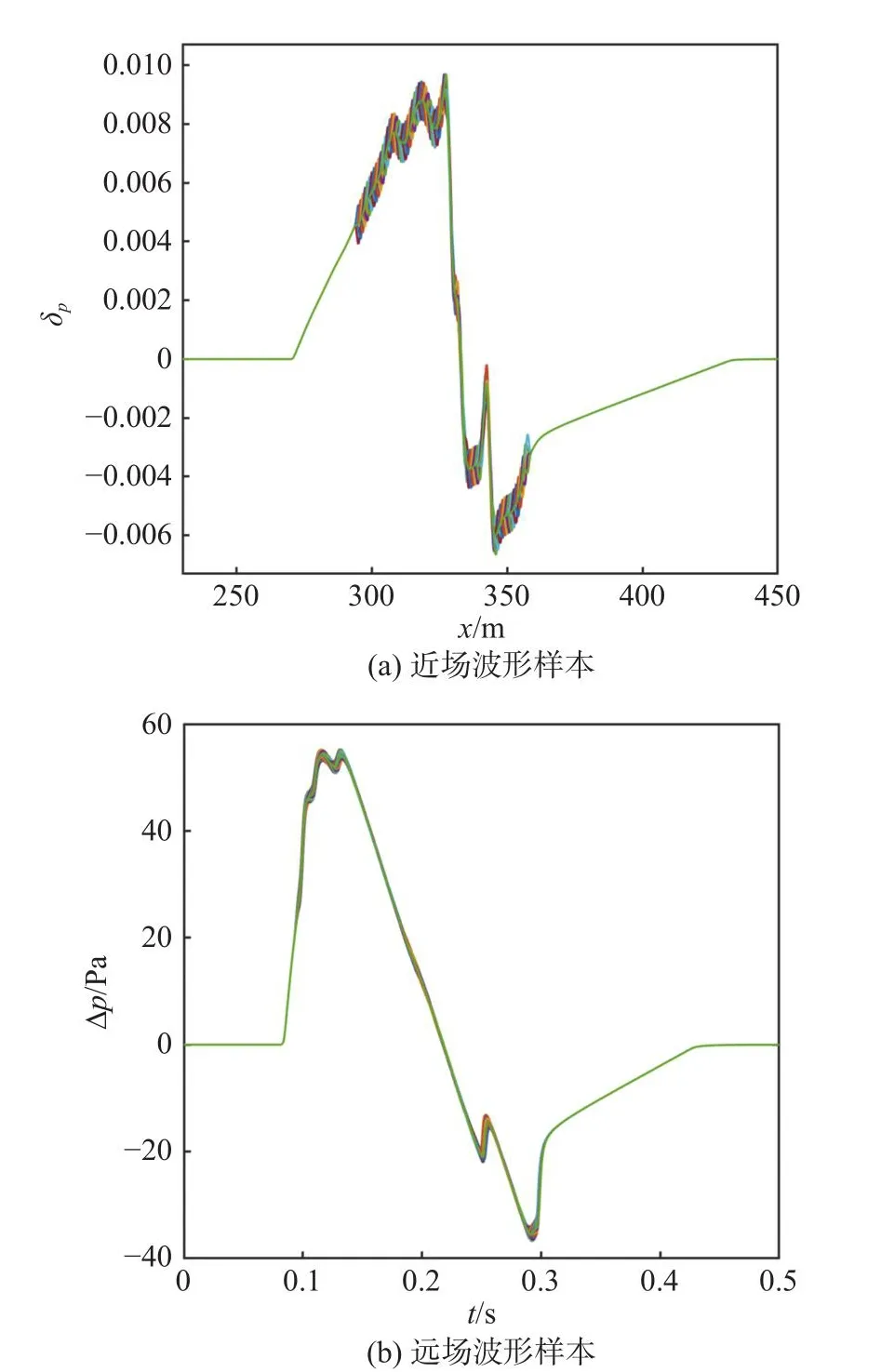
圖7 取樣得到的快照集Fig.7 Sampling snapshots

通過POD方法可以得到從大到小排列的若干特征值和與之對應的模態。圖8給出了前3階模態形態。設定目標能量值為99.9%，經計算，前21個模態可以滿足目標能量值的要求，可作為主模態來描述樣本空間。建立包含目標遠場聲爆信號的殘缺快照，使用GPOD方法修復。對上述“擾動取樣-POD”過程迭代計算，殘差定義同式（41）中的目標函數Ii，收斂條件為相鄰迭代步的殘差變化不超過1×10-5。共迭代400步收斂。

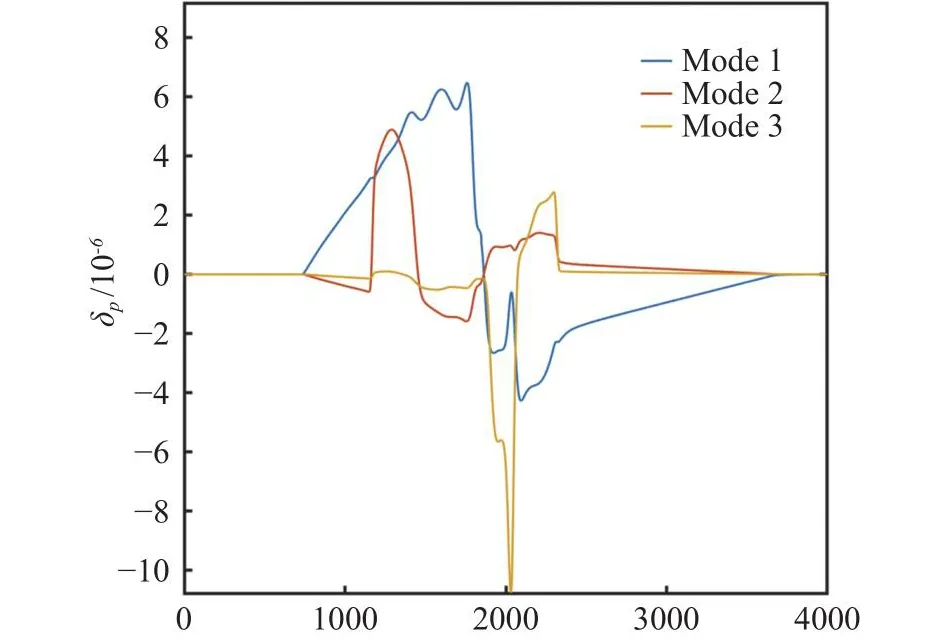
圖8 POD得到的前3階模態Fig.8 The first three POD modes

4.3.2 基于伴隨方程的聲爆信號細節反演

以逆向傳播結果作為初始值，其時間離散點對應的過壓值為設計變量，基于聲爆伴隨方程求解目標遠場聲爆信號對設計變量的梯度信息，并更新設計變量。使用序列二次規劃（sequential quadratic programming,SQP）算法尋優，收斂條件為相鄰迭代步的殘差變化不超過 1×10-5。

4.3.3 結果分析

圖9給出了兩種反演方法得到的近場聲爆信號。兩種方法對主膨脹波前的聲爆信號反演精度相當；對于主膨脹波后的聲爆信號，“逆向傳播+伴隨方程梯度尋優”方法得到的結果有更真實的物理細節。

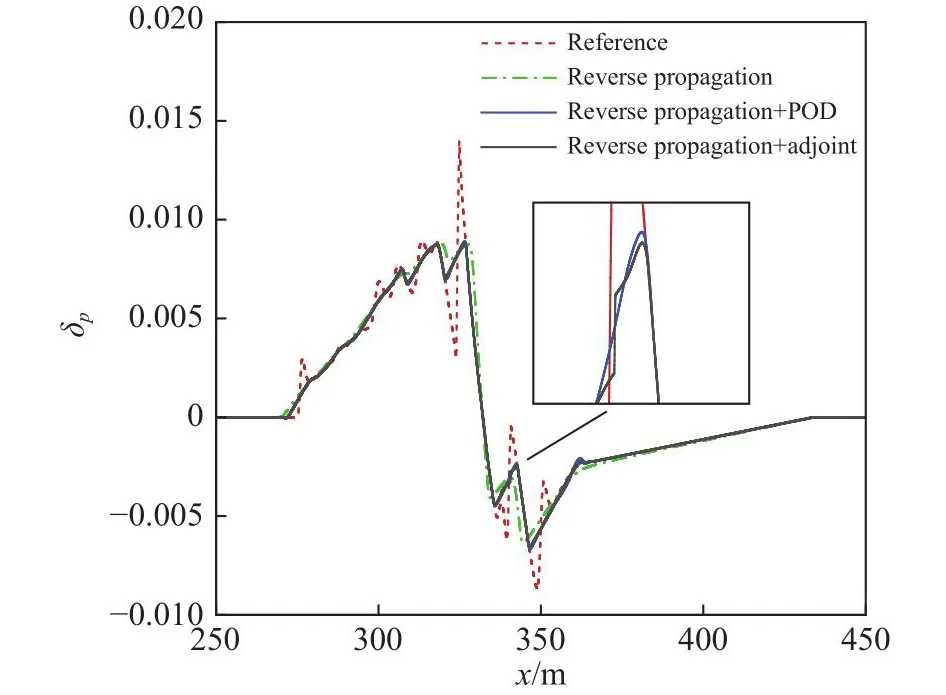
圖9 反演結果Fig.9 Reverse results

經過細節反演得到的近場過壓信號由增廣Burgers方程可得相應的遠場聲爆信號，如圖10所示。兩種方法的可信度良好，在尾部激波區，“逆向傳播+伴隨方程”反演方法的結果與參考值高度一致，而POD方法存在一定偏差。

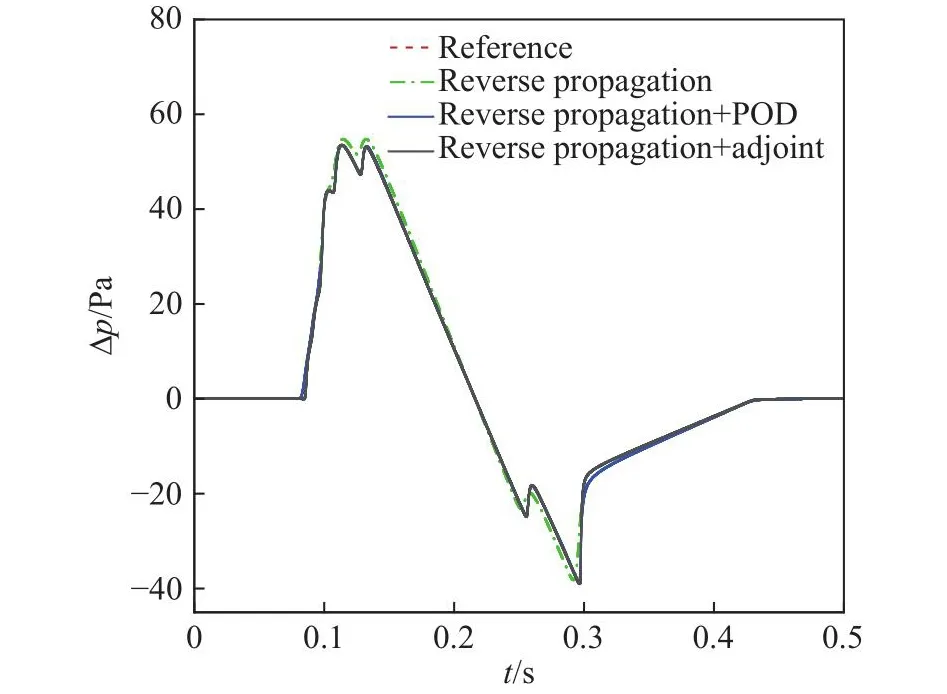
圖10 遠場聲爆信號驗證Fig.10 Far-field sonic boom signal verfication

遠場聲爆信號通過快速傅里葉變換（fast Fourier transform, FFT）得到頻域內的聲壓級、響度級分布，如圖11所示。圖11表明，僅通過逆向傳播得到的結果，相應的遠場聲壓級與響度級信號在中高頻區域誤差較大，原因是聲信號逆向傳播中激波信號耗散嚴重，表明了使用POD方法與伴隨方法還原波形細節的必要性。

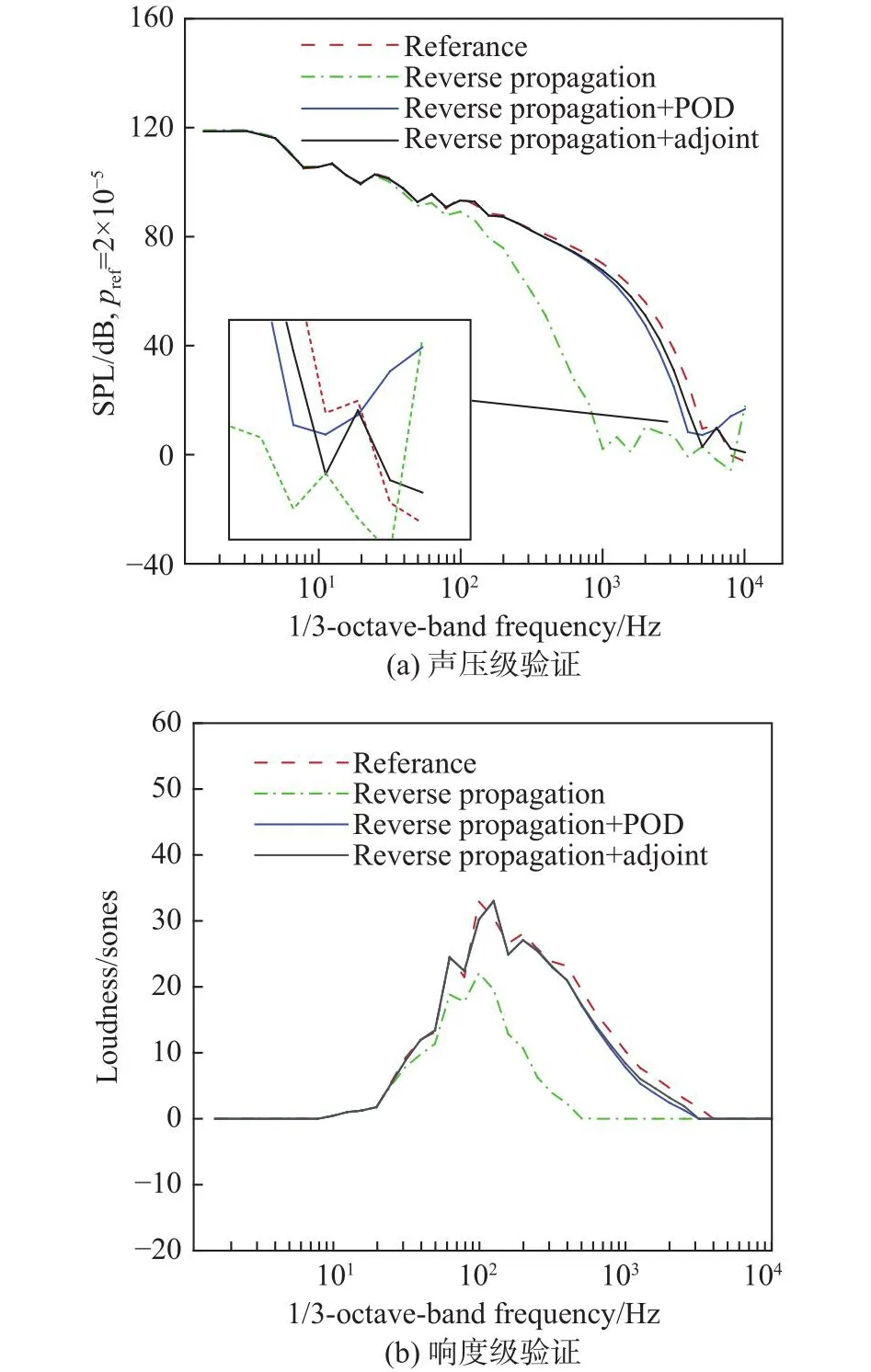
圖11 遠場聲爆信號的頻域特征Fig.11 Frequency domain characteristics of far-field sonic boom signal

“逆向傳播+伴隨方程”方法的反演結果，其遠場聲壓級與響度級高頻信號精度優于“逆向傳播+POD”方法。聲爆信號的高頻部分為激波，表明伴隨方法對激波信號的反演能力優于POD方法。

本文提出的聲爆反演方法旨在對人為設計的、達到適航要求的遠場聲爆信號進行反演，這一遠場聲爆信號主要參考感覺噪聲級（preceived noise level, PNL）進行設計。感覺噪聲級是根據三分之一倍頻程聲壓級計算出來的表示人耳感覺到的噪聲吵鬧程度的單一數字[35]，直接表征了聲爆信號對人耳的噪聲影響。反演方法的感覺噪聲級精度驗證如表1所示。

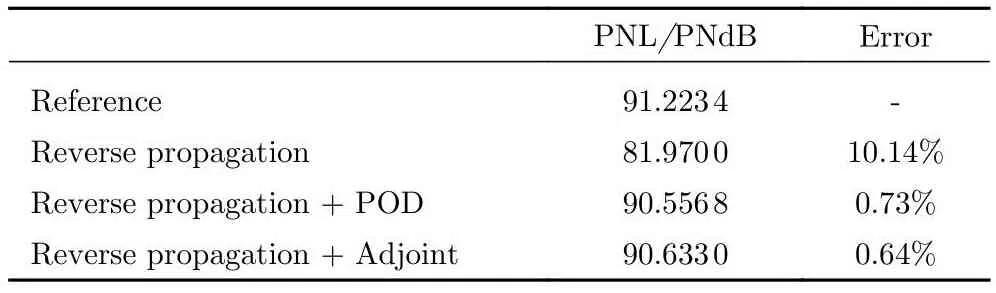
表1 感覺噪聲級對比Table 1 Comparison of PNL

兩種反演方法的感覺噪聲級精度較逆向傳播結果均有大幅提升，其中，“逆向傳播+伴隨方程”反演方法的精度高于“逆向傳播+POD”反演方法。

4.4 等效面積分布分析

等效面積分布是飛行器聲爆特性的決定性因素，因此也成為低聲爆綜合優化設計的指導函數。Abel算法可將近場聲爆信號轉化為飛行器的等效面積分布（EA），指導飛行器低聲爆氣動優化設計。其數學表達如式（42）所示。

圖12給出了兩種反演方法對應的等效面積分布，縱坐標為歸一化處理的等效面積。相對于逆向傳播結果，基于伴隨方程反演得到的等效面積分布均更接近參考值，表明局部激波信號丟失對等效面積分布精度有一定不利影響，本文提出的聲爆信號細節反演方法可有效降低這一影響。

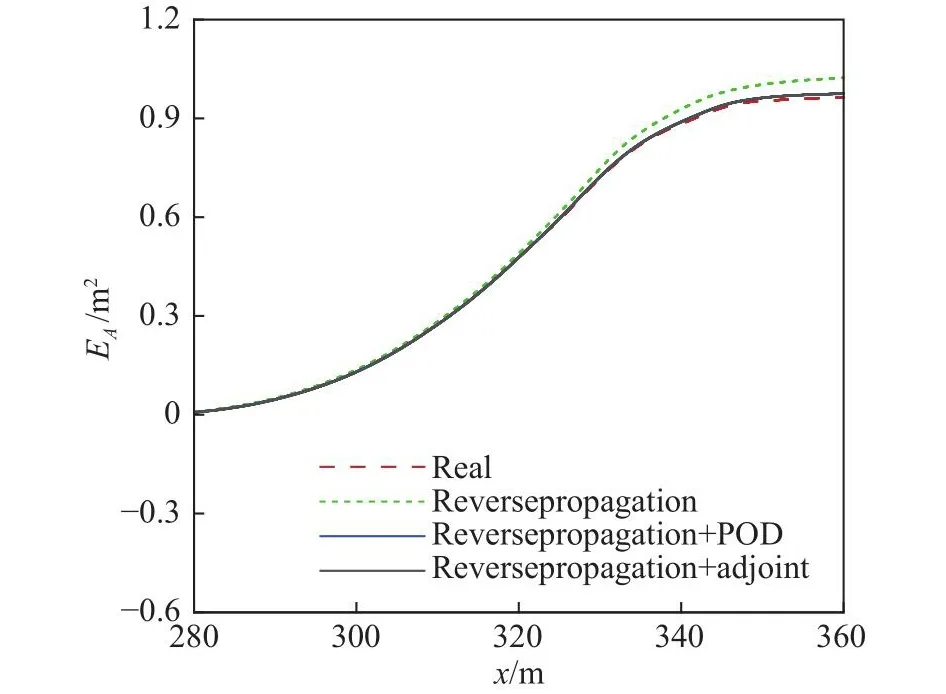
圖12 等效面積分布對比Fig.12 Comparison of equivalent area distribution

5 結 論

本文開展了“逆向傳播+POD”與“逆向傳播+伴隨方程”兩種超聲速飛行器近場聲爆信號反演方法的研究工作，驗證了其在低聲爆反設計優化中的可行性。該方法可進一步應用于未來超聲速民機的低聲爆設計，指導該類飛機的氣動設計和優化。相關結論如下：

1）遠場聲爆信號頻域內的聲壓級、響度級、感知聲壓級分析表明，僅經過逆向傳播得到的近場聲爆反演結果中局部激波信號丟失。而本文提出的兩種聲爆信號細節反演方法在逆向傳播結果的基礎上較好地還原了激波信號，感知聲壓級更精準。

2）盡管近場聲爆信號波形存在一定誤差，從遠場聲爆信號頻域分析與人耳感知聲壓級分析結果來看，基于本文提出的方法開展遠場聲爆信號的設計、反演與飛行器氣動外形優化設計是可行的。

3）聲壓級頻域分析結果表明，伴隨方程反演方法對聲壓中高頻信號（即激波信號）的反演更精準，因此“逆向傳播+伴隨方程”聲爆信號反演方法比“逆向傳播+POD”聲爆反演方法存在優勢。

4）由反演結果得到的等效面積分布與參考值吻合度較好，表明兩種反演方法能夠為后續基于等效面積分布指導的優化設計工作提供有力支撐。

下一步將根據遠場感知聲壓級設計聲特性良好的遠場聲爆信號，基于本文提出的反演方法得到相應的近場聲爆信號，進一步得到等效面積分布，開展低聲爆伴隨綜合優化設計。