出口分流裝置對振蕩射流流場的影響

楊 帆，溫 新，何創新，王士奇

(1.上海交通大學 機械與動力工程學院 葉輪機械研究所，上海 200240；2.中國空氣動力研究與發展中心 低速空氣動力研究所，綿陽 621000；3.中國航空發動機集團有限公司 中國航空發動機研究院，北京 101304)

0 引 言

振蕩器雖不涉及任何運動部件，但可以穩定產生高頻振蕩響應，因此被廣泛應用于流動控制領域，例如增強燃燒室混合[1-2]、環量控制[3]、翼型增升[4-5]、管內流動分離控制[6-8]、鈍體減阻[9-10]、增強沖擊換熱[11]和氣膜冷卻[12-13]，同時也存在一些特殊用途，例如產生矢量噴管所需的高頻次流[14]以及霧化高黏度液體[15]。在各類應用中，振蕩器均有良好的表現。

振蕩器的工作原理為：通過混合室以及反饋通道產生的雙穩態流動使其出口產生在給定平面周期性掃掠的射流。研究者為拓展振蕩器的適用場景，展開了廣泛的研究。例如，Nicholls等[16]通過聲波激勵控制振蕩頻率與相位；Tomac[17]通過在喉部增設流體入口，控制振蕩角度與傾斜角；Ostermann等[18]研究了振蕩射流與橫流互相作用時的流動特性。

然而，傳統連續掃掠式振蕩器出口射流衰減快，有效流動控制區域有限，且在如葉柵間隙等安裝空間受限工況中布置困難。所以研究者提出對其出口離散化形成脈沖式出口的改進（結構如圖1所示），從而彌補上述存在的問題，并可以在一定程度上提供傳統脈沖射流[19-20]以及合成射流[21-22]的替代方案，降低對快速閥門等特殊設備的依賴，拓寬應用場景。

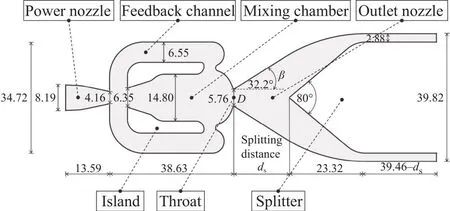
圖1 連續-離散脈沖式流體振蕩器的結構示意圖（單位：mm）Fig.1 Schematic of the continuous-discrete pulsing jet fluidic oscillator (unit: mm)

雖然類似上述的結構早在1964年[23]就已經出現，并且在2013年Wassermann等[24]和2021年Sang等[25]所研究的振蕩器構型中也已經包含分流楔結構，但是鑒于眾多研究均表明振蕩產生的核心為喉部前混合室和反饋通道等部分，所以研究重點均為上述結構。然而當應用于流動控制時，振蕩器實際出口（而非喉部后）的射流狀態往往是更加需要關注的，這就使得之前研究中被很大程度忽略的分流楔影響需要得到重視。Bobusch等[26]研究了分流楔對振蕩頻率和振蕩角的影響，但是限于其研究重點，對于相關問題僅能提供較為初步的結論。而具有類似結構的脈沖式振蕩器的流動機理（壓力變化規律[27]和流場結構演變[28-29]）雖然已經進行過研究，但是相關理論難以直接借鑒用于指導將連續掃掠式振蕩器變為離散脈沖式出口的改造。故本研究擬通過數值模擬揭示其流動過程，并探究分流楔前點與喉部中心間距（分流距離ds）對振蕩器峰值速度和振蕩頻率的影響。

1 研究問題與數值方法

1.1 研究問題

為應對連續掃掠式振蕩器出口流體能量分散、射流衰減快的特性，本文研究分流楔對于整體流動的影響。選用的實驗模型為圖1所示結構的連續-離散脈沖式振蕩器。工況如表1所示，選用三種設計模型：兩種分流距離ds=3D和 3.5D（D=5.76mm，為喉部間距）振蕩器及連續掃掠式振蕩器，進行了模擬計算。在結構上，連續掃掠式振蕩器喉部后無分流楔，從而出口射流可以在給定平面內進行周期性連續、往復掃掠，而在加裝分流楔后，連續-離散脈沖式振蕩器將形成兩股離散的周期性變化的脈沖射流。

表1 模擬工況Table 1 Simulation conditions

因為本文重點在于振蕩器內部流動，并且其可被視為準二維流動[26，30]，所以采用二維模擬。網格在各處壁面均有加密，以使其滿足湍流模型的要求（y+～1），并將計算資源集中于振蕩器內部流場。圖2顯示了所使用的計算域，由振蕩器內部與出口外部的空氣組成。外流場以喉部間距D為基準劃分。

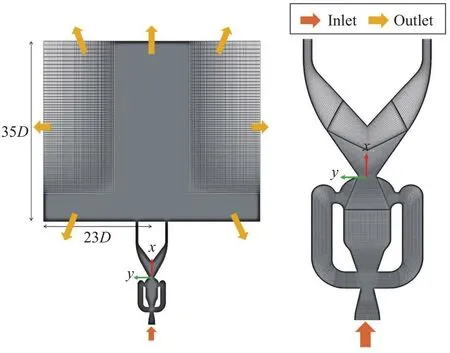
圖2 計算區域示意圖Fig.2 Schematic of the computational domain

1.2 計算方法與邊界條件

本文基于商用軟件Fluent進行流體力學分析，模擬計算方法參照Li等的工作[31]，使用Coupled算法進行壓力-速度耦合，采用 Generalizedk-ω（GEKO）湍流模型（參數見表2），工質為理想氣體，出、入口分別為質量流量入口和壓力出口（101 325 Pa，20 ℃，湍流度為1%），時間步長為0.01 ms。

表2 湍流模型參數選用表Table 2 Coefficients of turbulence model

采用構型ds=3.5D，入口質量流量m˙ =847.15g/s，監測振蕩器喉部中心點位置的速度變化頻率，共用三套網格，網格單元數量分別為6萬（731.5 Hz）、18萬（731.7 Hz）以及 35萬（731.7 Hz）。研究結果表明，網格滿足一定數量并分布合理時，在本文涉及的模擬工況中，振蕩頻率受網格數影響較小，故選擇第二密集的18萬網格作為計算網格。在不同構型網格劃分過程中保證了各自網格分布密度基本一致。

為了驗證計算模型，對構型ds=3.5D進行加工并保證流道高度等于喉部間距D，使得實驗件振蕩器喉部高寬比為1，本文模擬的對象可以視為該振蕩器的高度方向上中心平面內的流體[26，30]。實驗設置如

1.3 網格無關性以及模型正確性驗證

圖3（a）所示。實驗測量（模擬監測）振蕩器喉部中心壓力并計算變化頻率，結果如圖3（b）所示，表明上述模擬設置可以較為準確地預測該工況范圍內的振蕩頻率，其結果可用來分析其內部流場特性。

圖3 計算模型驗證結果圖Fig.3 Validation of numerical simulation

2 結果與討論

本節將通過速度曲線以及振蕩器內部流場的相對速度云圖，解釋連續-離散脈沖式振蕩器的出口速度三峰值特性，并確定各峰值速度的產生時間區間。

由圖4可觀察到兩出口速度（Uoutlet）變化頻率一致僅相位不同，并且在一個周期內至少存在三個（局部）峰值（如圖4中黑框標注所示）。而在長分流距離ds=3.5D的速度曲線（圖4b的藍色曲線）中的附加速度特征，將在第2.7節中討論成因。第2.1節至2.4節重點討論各工況中均存在的出口速度三峰值特性。

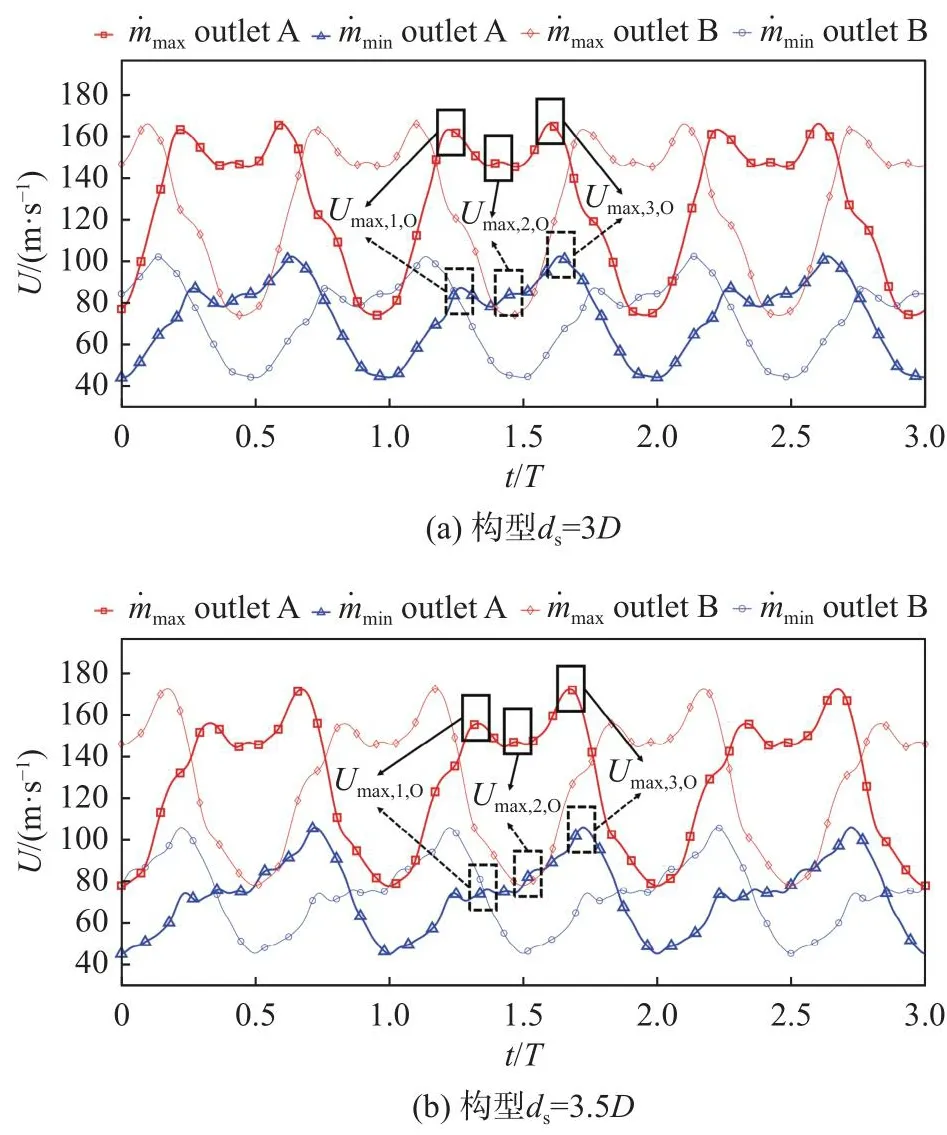
圖4 m˙ max和 m˙ min下出口速度隨時間變化曲線圖Fig.4 Evolutions of U outlet at the maximum and minimum flowrates the maximum and minimum flowrates

圖5、圖6分別給出了構型ds=3D在m˙max工況下Uoutlet隨時間的變化及部分時刻的相對速度分布云圖。相對速度定義如下：Urelative=U/Uinlet，其中U為振蕩器內各點的速度值，Uinlet為振蕩器入口的速度值。

2.1 連續-離散脈沖式振蕩器的出口速度特性

將Uoutlet達到最低并開始上升的時刻設為周期起點（圖5中a點）。此時射流正自B側向A側偏轉（如圖6a所示），更多射流進入A側（如圖6b所示）。在射流偏轉至A側最大角度前，A側出口達到第一峰值速度（Umax,1,O），對應圖5中點a-c的過程。圖6（d～f）有極其相似的喉部后流場，是因為射流偏轉角大于外壁面幾何角（ β =32.2°，見圖1），射流受外壁面約束保持該角度出流，期間速度上升到第二峰值速度（Umax,2,O），對應圖5中點d-f的過程。之后射流向幾何中心線偏轉，出口速度先降后升至第三峰值速度（Umax,3,O），如圖5點f-h所示。

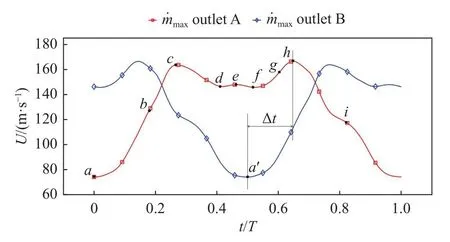
圖5 A、B兩出口速度隨時間變化曲線（ d s=3D ， m˙ max）Fig.5 Temporal evolutions of utions of U outlet,A andUoutlet,B in one cycle (d s=3D, m˙ max)

值得注意的是，A側出口速度（Uoutlet,A）下降起始點h與B側出口速度（Uoutlet,B）上升起始點a′的時刻間存在延遲 Δt，原因在于分流楔對射流的分束效果。由圖5 可知，a′點在點e、f之間，而圖6（e～f）表明此時射流主體雖仍在A側，但已有部分射流受分流楔的影響流向了B側，且該比例隨著偏轉過程的推進而上升，所以點a′早于點h。

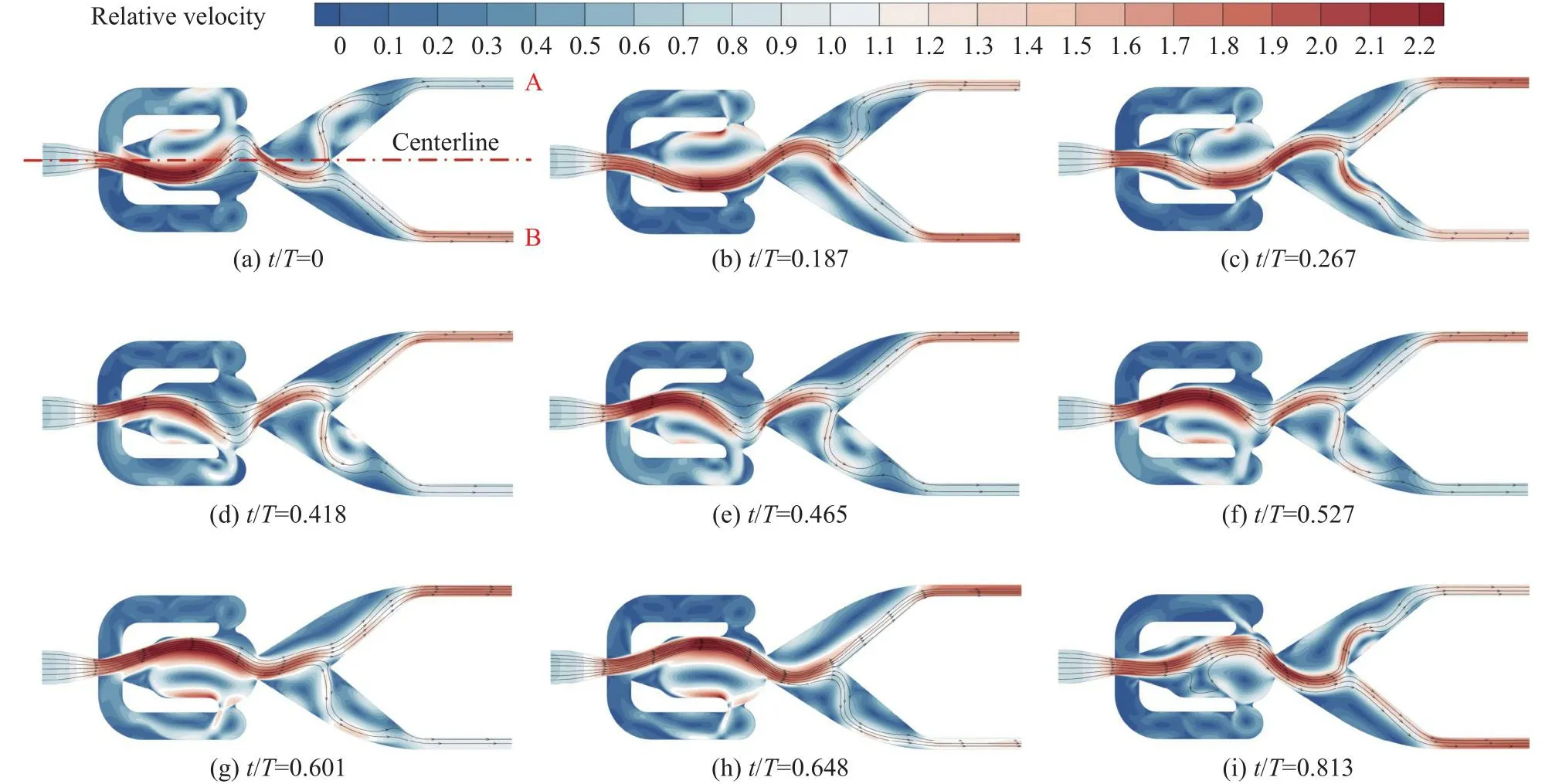
圖6 振蕩器內部流動示意圖（ d s=3D ， m˙ max）Fig.6 Instantaneous flow fields inside the oscillator (d s=3D, m˙ max)

綜上可知，Umax,1,O在射流自幾何中心線向最大角度偏轉期間產生，Umax,2,O在射流近乎停滯在最大偏轉角度的期間產生，Umax,3,O在最大角度向幾何中心線偏轉期間產生。

2.2 出口峰值速度的產生條件分析

本節將通過流動過程中射流形態和總壓的變化過程，分析不同空間區域、不同時間區間占據主導的損失，從而得到出口峰值速度的產生條件。

圖7為射流的相對總壓分布云圖。相對總壓定義為：prelative=p/pinlet，其中p為振蕩器內各點的總壓值，pinlet為振蕩器入口的總壓值。入口總壓值與后續流動相關程度高，所以pinlet,a≠pinlet,b。

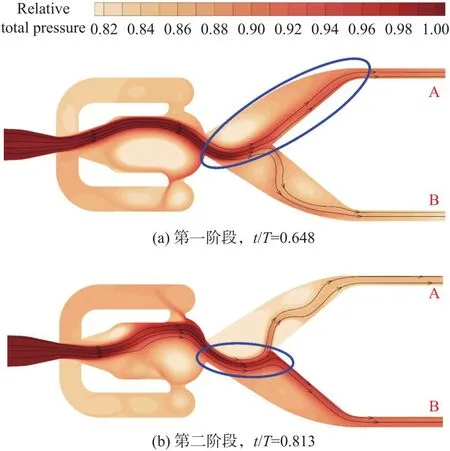
圖7 相對總壓變化云圖Fig.7 Contours of relative total pressure inside the oscillator

由圖7可將射流自喉部射出后的流動過程分為兩個階段，第一階段是未接觸壁面前的自由膨脹階段，第二階段是接觸壁面后的流向改變階段，兩個階段分別對應一類主導損失。前者可以由圖7（a）藍色圈中射流沿流動方向不斷降低的總壓來驗證，不可逆自由膨脹主導總壓的下降，此為第一類損失。圖7（b）藍色圈中射流接觸到壁面之后，流體速度方向被改變且喉部至近壁面處的總壓存在明顯的降低，印證了第二階段的存在，該階段中沖擊壁面造成的流動損失主導總壓的下降，此為第二類損失。

雖描述為兩個階段，但實際流動中兩個階段同時存在。圖7（a）中射流被分流時，A側流體的損失以第一類為主，B側射流與分流楔壁面接觸，損失以第二類為主。而圖7（b）中B側流體受分流楔導引，第二類損失占據主導，而A側流體則在轉向后，其損失主體偏向第一類。又或是對于一束射流，近壁面部分損失主體更接近于第二類，其余部分由第一類損失主導。

圖8為m˙max工 況下構型ds=3.5D的 單側Uoutlet、喉部中心速度（Uthroat） 及其速度角（α）隨時間變化曲線圖。圖9為相應的流場相對速度云圖。下文將借此深入分析影響Uoutlet的因素。

觀察圖9可知，射流偏轉過程中存在與偏轉方向相反的前端彎折現象，根據成因可分為兩類：第Ⅰ（Ⅲ）階段α＜β，射流自由振蕩（ β具體見圖1），對應圖8中點1（3）-2（4）的過程，射流前端彎折由流動形式的傳播延遲造成（如圖9a、圖9b）以及由分流楔作用造成（如圖9d）；第Ⅱ（Ⅳ）階段α＞β，射流振蕩受限，對應圖8中點2（4）-3（1）的過程，此時射流將在沖擊壁面后改變流動方向形成第二類彎折前端（如圖9g）。

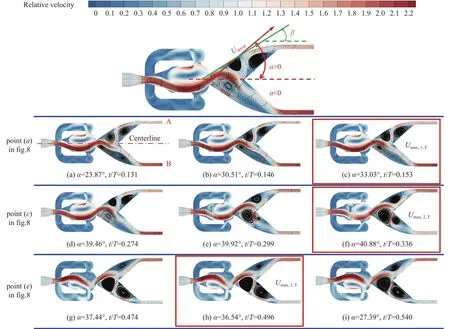
圖9 流場結構發展示意圖Fig.9 Flow field development

將射流分為近喉部未彎折部分以及前端彎折部分。對于前者，當α＜β時，更高的速度使射流可以更早地接觸外壁面結束自由膨脹，有利于Uoutlet提升；繼續偏轉至α＞β時，未彎折部分開始沖擊壁面造成更高的流動損失，不利于Uoutlet提升。而射流前端彎折部分沖擊分流楔壁面時會造成更大的損失并使流體進入另一側流道。同時Uthroat 的改變會直接使Uoutlet產生顯著變化。故可從流場參數角度出發，將上述的三種因素歸因于Uthroat和對應的α的變化。

綜上所述可以得到，出口峰值速度的產生條件為較大的Uthroat以及合適的α，使兩類損失最小的前提下提高射流速度，從而使出口速度可以達到峰值。

2.3 喉部速度與出口速度的相關性分析

本節將基于Uthroat與Uoutlet隨時間變化的曲線闡述兩者變化之間存在的延遲，同時對該值的區間范圍進行估算。然后基于第2.2節中得到的出口峰值速度產生條件，分析喉部與出口峰值速度之間的相關性，從而解釋出口三峰值速度的形成機理。

圖10為構型ds=3.5D的喉部中心速度Uthroat以及兩側出口速度Uoutlet隨時間變化的曲線。可以觀察到三者變化周期同為T，但是三者達到峰值速度的時刻之間存在不可忽略的時間差，如圖10中Δt1～Δt3和Δt1′～Δt3′所示，這主要因為射流偏轉時間與喉部流動形式傳播到出口所需時間處于同一量級。

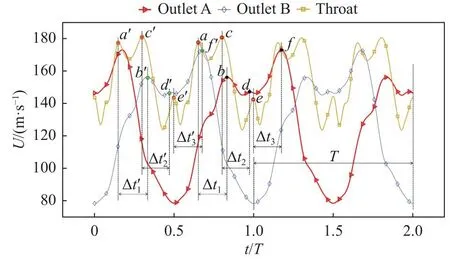
圖10 喉部速度與兩出口速度隨時間變化曲線（ d s=3.5D ，m˙max）Fig.10 Temporal evolutions of ns of U outlet andUthroat(d s=3.5D, m˙ max)

對圖10所示流動進行簡單的時間估算。Umax,1,O是在射流自幾何中心線向最大角度偏轉的過程中產生的，估算其時間尺度約為1/4周期，即≈0.68ms，而從喉部到出口流向距離（x方向）約為65.64mm，即使以全局最高速度（ 1 72.8m/s）也需要65.64×10-3÷172.8≈0.38ms，若是以全局最低速度（ 7 8.42m/s ）則需要 6 5.64×10-3÷78.42≈0.84 ms。由圖10可知，絕大多數時刻的速度處于兩者之間，所以流動過程中，流動形式從喉部傳播到出口所需時間應處于兩者之間，且與射流偏轉變化時間處于同一量級，從而導致Uthroat與Uoutlet之間存在相位延遲，且其范圍應介于 0.38ms～0.84ms。經過時間無量綱化（以周期T為無量綱參量），可得到該相位延遲范圍約為0.14T～0.31T。

接下來分析喉部峰值速度Umax,i,T與出口峰值速度Umax,i,O之間的相關性。以下提及的Umax,i,T（i=1～3）與圖8中點a、c、e分別對應，但是Umax,i,O（i=1～3）尚未被證明與圖8中點b、d、f相對應，故其僅代表某一出口峰值速度，既不代表各自產生的時序先后，也不直接表明Umax,i,O 由對應的Umax,i,T產生。

由第2.2節中出口峰值速度產生條件可知，Umax,1,O應 在Uthroat較高且兩類損失較小的時刻產生，所以圖8中α=β的Uthroat點2，至少對應一個較大的Uoutlet ，并可通過分析其前后時刻由Uthroat 與α引起的Uoutlet增減趨勢來推斷Umax,1,O產生時刻。因時間跨度較小，所以射流結構（主要指前端彎折程度）基本一致，如圖9（a～c）所示，為簡化問題，下文討論將忽略其影響。

對于稍前的時刻α＜β，自由膨脹使損耗增大，同時Uthroat降 低，兩相結合將使Uoutlet降低，無法產生峰值速度。而稍后的時刻α＞β，沖擊損失增大，但是Uthroat升 高，因為此時Uthroat對 于Uoutlet的效果更為顯著，所以Umax,1,O應在平行時刻稍后的某一時刻產生。這自然聯想到與平行時刻十分接近的Umax,1,T（圖8點a），速度最高同時αmax,1,T=33.03接近 β ，且在其之后，因為α增大Uthroat下降，損失增大流量下降，不再具備產生Umax,1,O的 條件。綜上可知，Umax,1,O是由點a代表的Umax,1,T產生的。

在Umax,2,O的產生時期內，喉部后A側流道內射流結構幾乎不變，如圖9（d～f）所示。鑒于α＞β，主導的損失應為沖擊導致的流動損失，所以α越接近 β ，那么損耗將越小。再結合Uthroat的變化情況，因為圖8中點c前后的α均增大Uthroat均減小，不利于Uoutlet，故可以推斷Umax,2,O是 由點c代表的Umax,2,T產生的。

Umax,3,O產生時期內，射流已經開始自A側最大角度向幾何中心線偏轉，即α有整體下降的趨勢。因為圖8中點c后的α與Uthroat的變化趨勢均偏向負面（流量減小損失增大），故可知潛在區間為其之后的階段Ⅱ與Ⅲ的交界區域。分析可知交界點3之后，隨著α與Uthroat的減小，Uoutlet降低，無法產生Umax,3,O。再以圖8中點e作為研究對象，其前時刻α變化較小，但是Uthroat下降明顯，所以相應的出口速度應低于點e對應的值；而對于點e之后的時刻，速度下降更為明顯，雖α更接近 β ，但也無法產生Umax,3,O。故可以得到，Umax,3,O是 由點e代表的Umax,3,T產生的。

綜上可知，每一個喉部峰值速度Umax,i,T均對應產生一個出口峰值速度Umax,i,O，即圖8中點a、c、e所代表的Umax,i,T與點b、d、f所代表的Umax,i,O存在對應關系。

然后結合本節開頭對于喉部速度與出口速度的延遲范圍的估算，可以排除超出范圍的不合理對應關系。例如，圖8中點a所代表的Umax,1,T與點f所代表的Umax,i,O，兩者間時間間隔過長，無法形成對應關系；又如點c所代表的Umax,2,T與點b所代表的Umax,i,O，兩者時間間隔過短，也無法形成對應關系。

綜上可以得到圖8中點a、c、e所代表的Umax,i,T與點b、d、f所代表的Umax,i,O依次一一對應，分別為喉部/出口第一至第三峰值速度。

這里需要說明的是，上文雖將Umax,i,T描述為Umax,i,O的產生原因，但是實際上的產生時刻可能在Umax,i,T時刻前后有極小的偏移，其原因在于分析中提到的正負面作用的互相平衡，但僅對于流動現象的解釋而言，這樣的描述是方便理解且不包含本質性錯誤的，所以采用這樣的描述方法。

2.4 整體流動過程分析

本節將基于第2.2節得到的出口峰值速度產生條件與第2.3節得到的喉部速度與出口速度的相關性，結合流場結構的演變，解釋振蕩器出口三峰值速度之間轉變過程，從而解釋出口速度曲線的形成機理。

由第2.3節得到的喉部與出口峰值速度一一對應關系，可以將Uthroat和α相位平移，并以三峰值速度時刻作為基準點，把圖8轉換為圖11的形式，而圖12則是對應的喉部后流場的相對速度分布云圖。

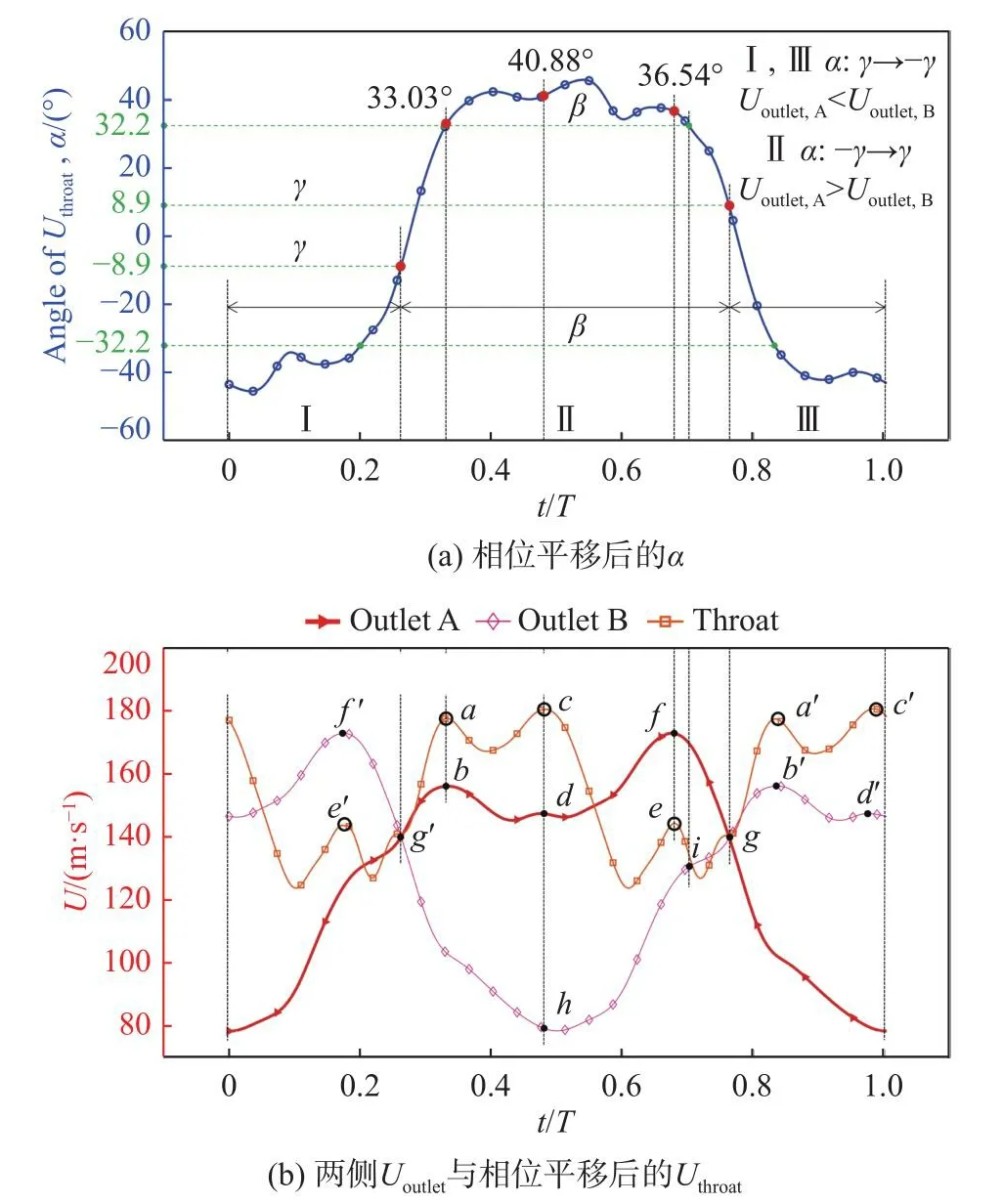
圖11 U outlet 與相位平移后的 U throat ，相位平移后的α隨時間變化曲線（ d s=3.5D ， m˙ max）Fig.11 Temporal evolution of U outlet , and phase translatedUthroat and α (d s=3.5D, m˙ max)

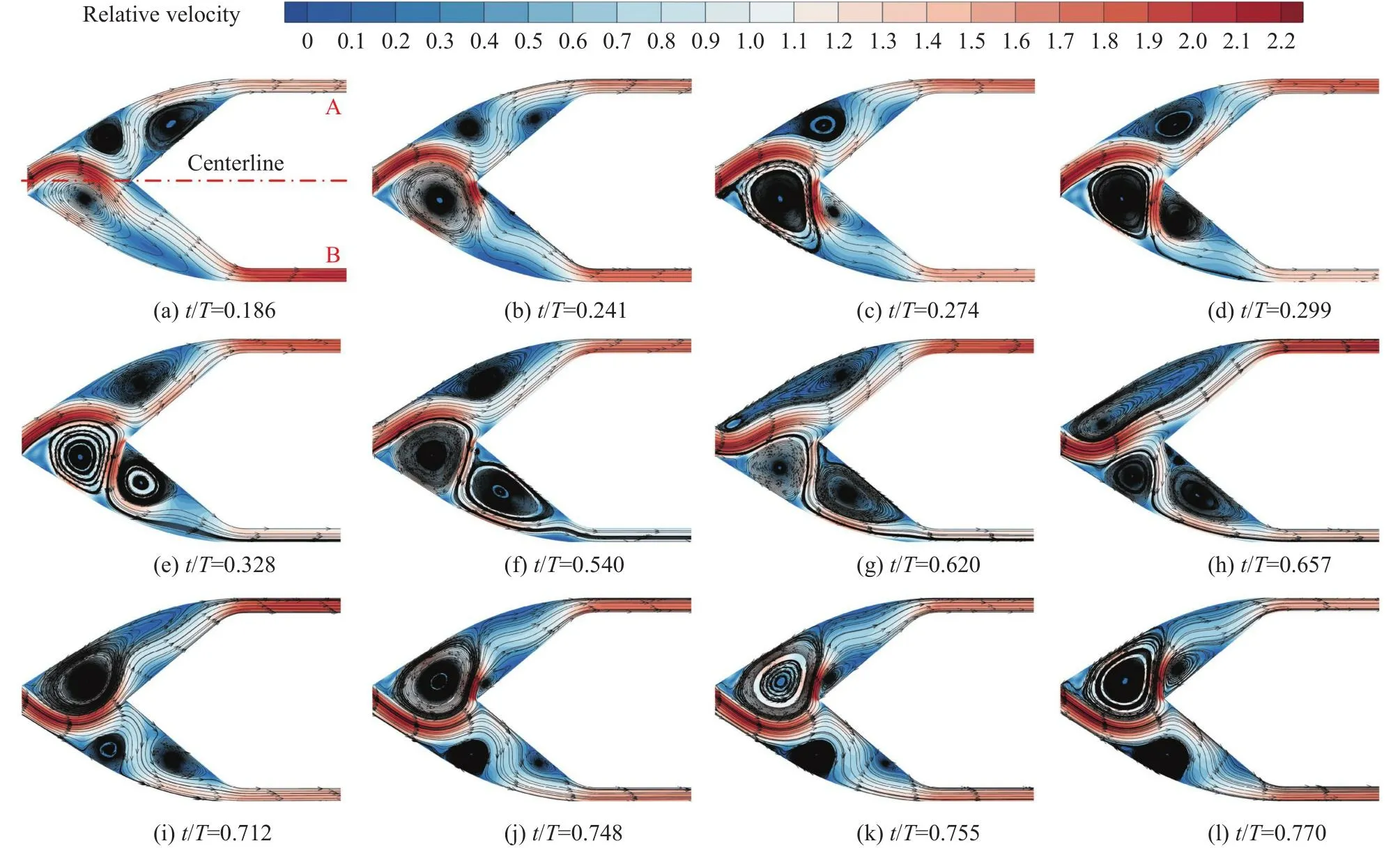
圖12 喉部后流場發展過程示意圖（ d s=3.5D ， m˙ max）Fig.12 Flow field development downstream of the throat (d s=3.5D, m˙ max)

圖11中點a-c（b-d）為Umax,1,O向Umax,2,O的轉變過程。點a之后Uthroat下 降、α上升，表明流量下降、損失提高，對應點b后的速度下降段。從圖12（c～d）可知，此時因為射流動能不足，α過大，使射流沖擊分流楔壁面后無法很好保持附壁流動，遠離壁面部分的流線產生彎曲，A側外壁面渦不斷擴大，最終導致Uoutlet,A下降。之后點c前Uthroat上升、α減小，使流量上升、損失減小，對應點d前的速度上升段，流場如圖12（e）所示。與圖12（c～d）相比，流線在分流楔和出口等直段過渡更加平滑。

圖11中點c-e（d-f）為Umax,2,O向Umax,3,O的轉變過程如圖12（f～i）所示。隨著α由正向負減小，A側外壁面渦逐步前移，射流流線不再如圖12（b）有多次轉向，而是平滑附著于分流楔壁面流動，提高Uoutlet,A。但是在上述過程中Uoutlet,B也在同步上升，如圖11中點h-i（d-f）的過程所示，這代表流向B側的分流在增多，該上升過程有著不同形成機理的兩階段，首先是由于射流離開喉部后大角度沖擊A側外壁面并與分流楔作用之后產生的逐漸增強的B側分流，同時因為該分流在B側流道無法平滑附壁流動，造成了B側分流楔壁面的渦流區域，該階段流場如圖12（f～h）所示，后一階段是由于α小范圍波動時Uthroat的持續增長而導致的，其流場如圖12（i）所示。

值得注意的是，分流楔使α不需要越過 0°射流就可以切換流道。如圖11中所標示的點g（α=γ ≈8.9°），B側Uoutlet超越了A側Uoutlet，而圖11中點g'則代表著相反的過程。

射流繼續向B側偏轉，Uthroat和α一起減小，A側的流量下降、自由擴散損失上升，射流動能的持續降低使A側分流楔壁面出現渦流區域，如圖12（i）所示，降低Uoutlet,A。而B側，越過g點的射流向下游吹離兩個渦流區域，并且分流楔表面的渦流區域持續減小，如圖12（i～l）所示。當其平滑貼合流動后，Uoutlet,B快速上升至Umax,1,O點b′。之后往復循環上述過程，呈現出圖11中所示的速度變化規律。

2.5 入口流量和分流距離對于峰值速度的影響

本節基于上文對于出口峰值速度的分析，闡述入口流量和分流距離對于峰值速度影響。

圖13（a）為兩構型三峰值速度隨入口流量變化的曲線。大多數模擬工況下，但Umax,1,O有 隨m˙ 同向變化的趨勢。由圖11可知，大小關系相反。同時也得到αmax,i,O= 33.03°，40.88°，36.54°（i= 1～3），其中由αmax,2,O最高可知此時射流沖擊外壁面最劇烈，導致流動損失最高、彎折程度最嚴重且有更多射流進入B側流道，所以Umax,2,O最低。

圖13 出口峰值速度隨入口質量流量及分流距離的變化Fig.13 Outlet peak velocities for different m˙ and ds

Umax,1,O＜Umax,3,O的原因在于后續射流的影響。如圖11所示，在喉部達到Umax,1,T（點a）后，α繼續上升使彎折加劇，并有更多射流進入B側，不利于提高Uoutlet,A 。但是Umax,3,T （點e）之后，α整體下降并越過β，則沖擊損失下降同時彎折減弱，更多流體留在A側流道，有助于提高Uoutlet,A ，故Umax,3,O＞Umax,1,O。

但因m˙ 減小（增大）會令射流衰減變快（慢），使有效ds變長（短），上述規律有如下變化：

1）當m˙ 減小時，Umax,1,O有 下降并低于Umax,2,O的趨勢。因為兩者產生時，均存在彎折使部分射流進入另一側流道的現象，只是由于αmax,1,O較小，使損耗比分流小，所以才有Umax,2,O＜Umax,1,O。 但當m˙ 減小時，ds變 相增長，削弱了上述因素的影響，加之Umax,2,T＞Umax,1,T ，所以使得低流量下Umax,2,O＞Umax,1,O。

2）當m˙ 增大時，Umax,1,O有 上升并超過Umax,3,O的趨勢。m˙ 增大使ds變 相縮短，使主要影響Umax,1,O提高的分流比下降，但Umax,3,O是在射流自最大角度向幾何中心線偏轉的過程中產生的，分流效果相對而言并不明顯，加之Umax,1,T＞Umax,3,T ，所以Umax,1,T 才能隨m˙增大逐步接近Umax,3,O。

通過圖13（b）進一步解釋ds對出口峰值速度的影響。圖中Umax,1,O，短ds（ 紅色圓標線）均大于長ds（藍色圓標線）；Umax,3,O則 是長ds（藍色粗實線）均大于短ds（紅色粗實線），且兩者差值基本不隨流量變化。而Umax,2,O則 是長ds（藍色細實線）略小于短ds（紅色細實線）且隨流量變化，兩者有接近的趨勢。

對于Umax,1,O，射流前端自A側向B側彎折，如圖12（a～c）所示，ds越長，則越多射流進入B側流道。Umax,3,O與之相反，彎折方向自B側向A側，如圖12（h）所示，增長ds使分流延后，因此有更多射流留在A側，從而解釋了圖13（b）中這兩個峰值速度不同ds下的較為均勻的差值以及相應的大小關系。

Umax,2,O在α遠大于 β 時產生的，彎折現象嚴重，且有更多射流進入B側流道。彎折類似Umax,1,O，雖然縮短ds的確有助于留住更多流體，但因為彎折過于嚴重，所以模擬的兩種ds對Umax,2,O均無明顯影響。值得注意的是，隨著m˙ 增 大或減小，兩構型的Umax,2,O都有靠近的趨勢。原因在于，ds縮短會使射流沖擊損失增大但分流比下降；反之，ds增長則使射流沖擊損失降低但分流比上升；正負作用平衡，使m˙ 變化帶來的等效ds變 化導致兩端的Umax,2,O接近。

2.6 分流楔對于振蕩頻率的影響

圖14是各流量下兩種構型的連續-離散脈沖式振蕩器和連續掃掠式振蕩器振蕩頻率的對比圖。可以觀察到，在上文分析的五種模擬工況下，頻率有連續掃掠式振蕩器（fcon） ＞短分流距離（fshort）＞長分流距離（flong）的關系。但是隨著m˙ 上升，fshort與flong逐步接近。在額外對更大流量進行模擬后發現，當m˙ 超過一定范圍后，flong將超越fshort，振蕩頻率大小關系變為fc on＞flong＞fshort。

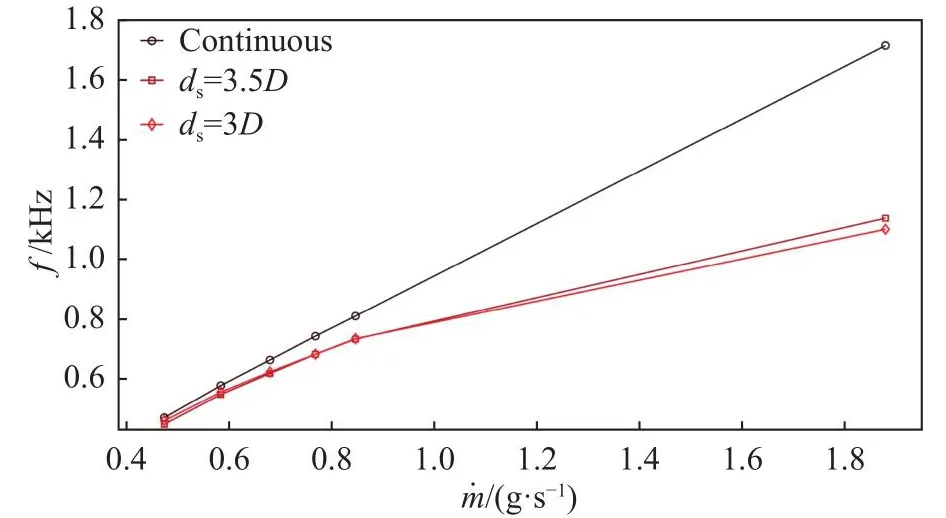
圖14 振蕩頻率隨分流距離的變化Fig.14 Oscillating frequencies for different ds

圖15是m˙max下三種構型的時均相對總壓和相對速度云圖。掃掠式振蕩器喉部后總壓下降最快，但中心區域流速最快，如圖15（a）所示，表明流體可以快速遠離喉部，不造成擁塞。但是加上分流楔后，雖使射流能量集中，但也會增加流動損失并使喉部后擁塞，如圖15（b-c）所示。并且隨著m˙ 增大，ds變相縮短，將加劇擁塞。故fcon始 終最高，并且m˙ 越大，fcon與fshort 及fl ong的差值越大。

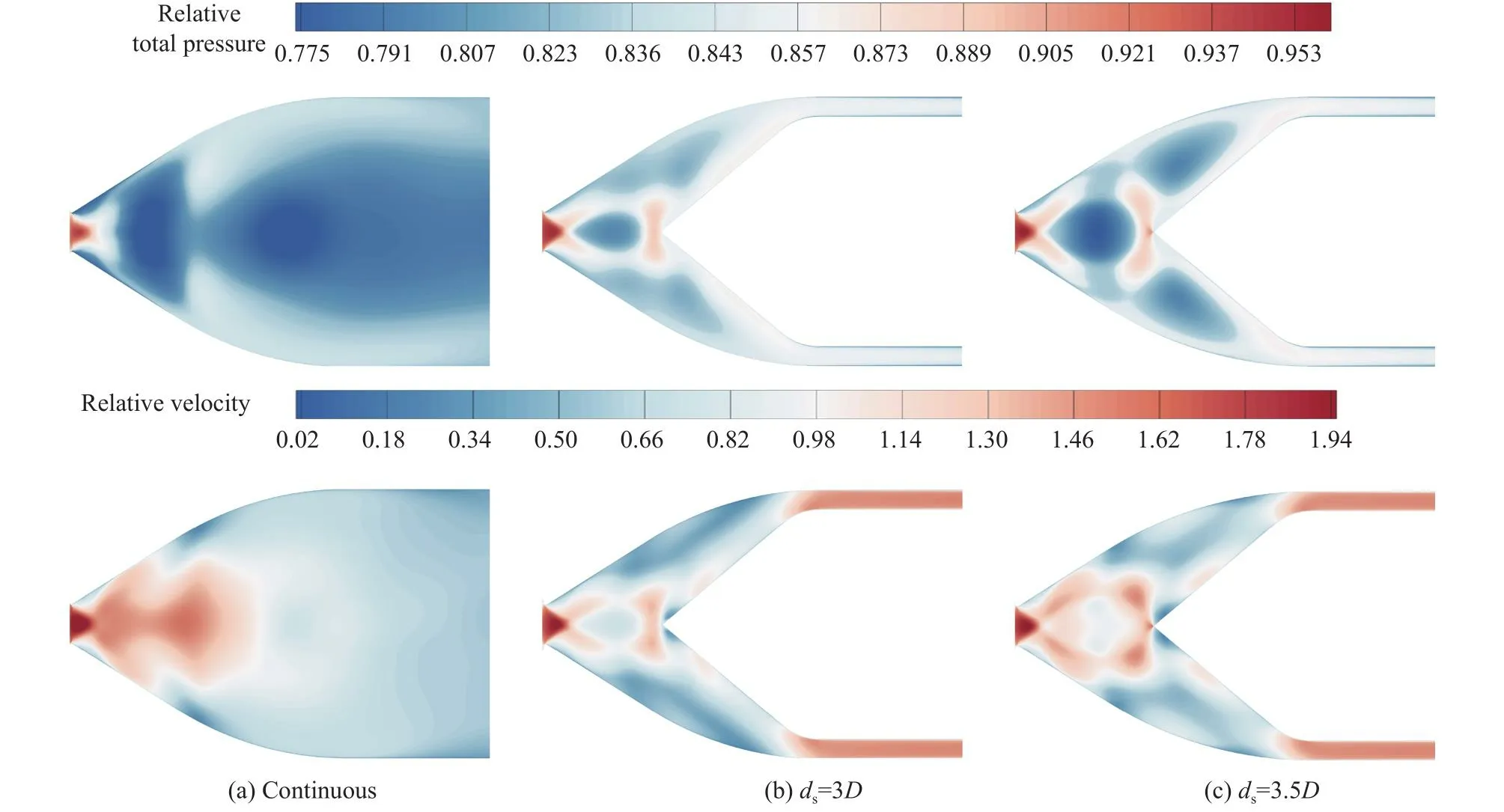
圖15 不同分流距離下的喉部后時均流場（ p relative 和 U relative）Fig.15 Time averaged p relative and U relative downstream of the throat at m˙ max and different ds

對于有分流楔的振蕩器而言，振蕩頻率的高低由喉部后擁塞現象的嚴重程度決定。當縮短ds，自由膨脹階段縮短，分流楔前的總壓損失降低，如圖15（b～c）中短ds（b）的水滴狀低總壓區域遠小于長ds（c）的對應低總壓區域，但這也導致射流以更高的速度與壁面接觸，流動損失更高。而增長ds則相反，更多總壓損失在第一階段，但第二階段的總壓損失會相對降低，如圖15（b～c）中長ds（c）的分流楔前高總壓弧形區域大于短ds（b）的對應高總壓區域。所以當m˙較 小時，因第一類損失占主導，所以短ds占據優勢；當m˙ 超過一定量后，因第二類損失占主導，長ds占據優勢。這解釋了圖14中長ds的振蕩頻率（深紅線）先小于、后大于短ds的振蕩頻率（紅色線）的原因。

2.7 特殊工況下的流動分析

本節討論第2.1節中m˙min工況下、構型ds=3.5D所呈現出的不同流動現象。將基于該構型不同流量下的速度演化過程展開分析。

圖16為各流量下構型ds=3.5D的Uoutlet和Uthroat隨時間的變化曲線。在第3.3節中所分析的是最大流量工況（紅色線），通過觀察其峰值速度特征點，可以尋找到最小流量工況（藍色線）對應的速度峰值點，并以此作為階段分界點，分析該速度曲線的成因。

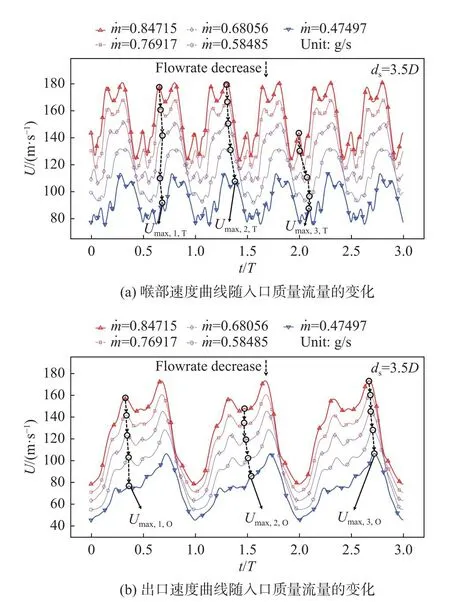
圖16 喉部和出口速度隨分流距離的變化Fig.16 U outlet and U throatat different inlet flow rates flow rates

類似第2.4節的分析過程，可以得到圖17，其中下標i代表自喉部進入出口段的速度特征點，下標o代表自出口離開振蕩器的速度特征點。由于無法進行相位平移來進行對應，所以圖中采用相同的字母表示對應關系。同時圖17中bi/o、di/o、fi/o依次為上文所述的喉部/出口第一至第三峰值速度點。

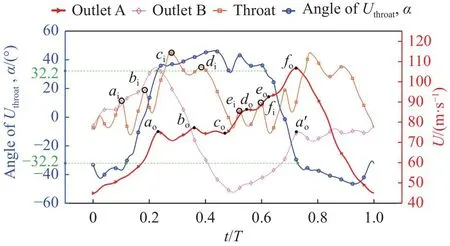
圖17 U outlet , U throat和 α隨時間的變化（ ds =3.5D, m˙ max）Fig.17 Temporal evolutions of utions of U outlet ,Uthroat and α (d s=3.5D, m˙ max)

最大的區別在于Umax,1,O前后的速度波動、整體相位的變化以及Umax,2,O幅值的變化。前兩種變化的產生原因類似，均存在來自于兩方面的影響：一是來自分流距離ds的 影響，由于ds的增長使分流楔對喉部射出的流體影響減弱，更加自由的擴散放大了喉部速度波動，這也不可避免地影響到喉部速度的相位；二是來自入口流量m˙ 的影響，因為隨著流量m˙ 的降低，射流更易衰減，從而在射流來回掃掠時產生的外壁面渦流增強，這使得喉部速度相位發生較大變化，而增強的渦流也會使喉部速度產生更多的波動，如圖16（a）所示。故此可知，無論是ds的增長或是m˙ 的降低，對于喉部速度波動以及相位均有影響，但各有偏重，從而再經過出口段的速度演化，最終形成了該特殊工況下出口速度的波動及整體相位的變化。

而Umax,2,O幅 值的變化是由于m˙的 降低后ds變相增長，在α偏大時，如圖17中c-d段，喉部速度的減小在射流整體速度較低、容易衰減的條件下反而有助于緩解大角度沖擊外壁面時射流前端彎折現象，使得更多流體留在A側流道之中，從而提高Umax,2,O。

更多的出口速度變化規律與第2.4節中描述的m˙max工 況類似。一般來說，Uthroat的 上升有利于Uoutlet，相反則可能導致Uoutlet下降；而對α而言，與 β 越接近越有利于Uoutlet。在這一工況中較為特殊的是，當α＞β時，Uthroat的下降緩解了射流前端彎折現象，使更多流體留在A側，如圖17中點co后的加速段。類似的還有由于Uthroat下 降，α超越 β 繼續增長，使更多的流體留在A側，但總流量降低，造成圖17中點do所在的平緩變化段。相反，當α＞β時，Uthroat繼續上升，則會導致彎折加劇，使得Uoutlet下降，如圖17中點ci前Uthroat持 續上升，α在 β 之上浮動變化，造成點co前的Uoutlet下降。而在第2.4節中圖11點c（d）后的緩慢加速段也是類似的原因，只是由于其Uthroat更高，射流彎折后更易進入B側流道，分流加劇，從而使得Uoutlet上升并不明顯。此外，值得注意的是，往往Uthroat與α對Uoutlet的影響并不是同向的，其導致Uoutlet的變化需要由兩者各自對流動的影響程度來決定。如圖17中點ei段，Uthroat與α同時增大后減小，均產生了點eo所在的Uoutlet增長段，只是增速不同。

3 結 論

本文采用二維非定常方法模擬了pinlet= 126.3～166.3 kPa五種入口壓力工況以及兩種分流距離ds=3D和 3.5D的連續-離散脈沖式振蕩器以及連續掃掠式振蕩器的內部空間流場，得到以下結論：

1 ）由于分流楔結構以及振蕩射流的偏轉流動形式，連續-離散脈沖式振蕩器的兩個出口在一個周期內均存在至少三個不同的速度峰值：

① 對于不同入口質量流量m˙ ，出口峰值速度但m˙ 增大時Umax,1,O上升甚至有超過Umax,3,O的 趨勢，而m˙ 減小時Umax,1,O下降甚至有低于Umax,2,O的趨勢；

② 對于不同分流距離ds，ds增長時Umax,1,O下降，Umax,3,O上升，而Umax,2,O受到影響較小。

2）喉部中心的振蕩頻率對于一定范圍內的入口質量流量存在fcon＞fshort＞flong的關系。當m˙ 增長超過一定范圍后，flong超過fshort，但fcon仍為最高且差值隨流量增大而增大。

3）當分流距離一定時，入口流量的降低會使喉部后射流衰減加快并且變相增長分流距離，從而減弱分流效果以及分流楔對喉部出流的影響，導致出口速度特征發生改變，包括在Umax,1,O前后產生顯著速度波動、整體相位的變化以及Umax,2,O幅值的變化。而入口流量升高時的工況還有待進一步研究。

需要指出的是，該研究結果可以為優化連續-離散脈沖式振蕩器及相關流動控制方案設計提供支撐。但是該研究參數有限，下一步研究重點將放在更廣泛的流動工況和更多出口段結構參數下的流動規律研究。

致謝：感謝宋金升、周鑾良在數據分析、論文寫作等多方面的啟發與幫助。感謝李子焱在數值模擬計算方法的指導。