圖論模型與算法在航天器下行數據故障診斷知識循環依賴缺陷檢測中的應用

王 蕊 沈 星* 吳 偉 潘順良

(1.南京航空航天大學航空學院, 南京 210016; 2.北京東方計量測試研究所, 北京 100094;3.北京空間飛行器總體設計部, 北京 100094)

1 引言

為確認在軌航天器的運行狀態,保障飛行任務的正常開展,地面飛控人員需要實時監測航天器下行的遙測參數,并對其正確性進行診斷。隨著航天器構造越來越復雜,下行遙測速率也越來越高。得益于中國第二代中繼衛星天地測控通信系統的建設,目前天和核心艙的下行遙測速率已經達到了1.2 Gbps[1],較天舟系列貨運飛船提升了1 個數量級[2],較神舟系列載人飛船提升約3 個數量級[3]。中國空間站構造復雜,并常駐航天員,其下行遙測參數的故障診斷不能簡單地依靠若干門限,必須考慮各遙測參數以及上行遙控指令之間的依賴關系。

中國空間站等航天器從地面電性能測試開始就配套故障診斷系統[4],并最終在軌應用。航天器下行數據故障診斷系統屬于專家系統[5-7]的一種,其核心在于專家知識庫和推理引擎[8-9]。故障診斷推理引擎根據存在于知識庫中的診斷知識,依據下行遙測參數和上行遙控指令,得出各遙測參數是否正常的結論,并發布給地面飛控人員。對于專家系統而言,知識獲取是制約其應用的瓶頸問題[10]。雖然研究人員針對航天器下行數據故障診斷系統錄入了大量的診斷知識,但其中依然存在缺陷的診斷知識,其中較為典型的一類知識缺陷是循環依賴,比如遙測參數A 的診斷知識依賴于遙測參數B,而遙測參數B 的診斷知識又和遙測參數A 相關。

圖論[11-12]是應用數學的重要分支,從經典的哥尼斯堡七橋問題[13]、哈密頓圈問題[14]等,到現代的機器學習算法[15-18],圖論都發揮了重要的作用。本文將遙測參數診斷知識中蘊藏的依賴關系抽象為有向圖中的頂點和有向邊,把診斷知識中的循環依賴檢測問題抽象為有向圖中的環搜索問題,應用經典拓撲排序算法、Kosaraju 算法[19]、Tarjan 算法[19]及本文提出的改進Tarjan 算法開展診斷知識的缺陷檢測。

2 診斷知識分析

2.1 故障診斷知識庫

為實現航天器下行數據的故障診斷,中國空間站等航天器采用了基于腳本的故障診斷系統。對于每個遙測參數,都可以錄入一段診斷腳本,描述遙測參數所屬設備或子系統的運行狀態以及切換過程,并明確該遙測參數在不同狀態下的值域判斷邏輯,如圖1 所示。

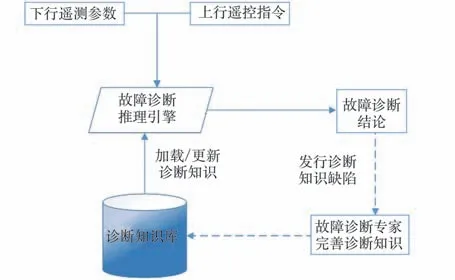
圖1 航天器下行數據故障診斷系統示意圖Fig.1 Schematic diagram of spacecraft downlink data fault diagnosis system

圖2 是其中一個典型的診斷知識示例,描述了某電壓量遙測參數A001 的診斷知識。其狀態切換與SBKJ、SBGJ、QBF、QZF 等上行指令相關,而其值域則與某電流量遙測參數A002 相關,即遙測參數A001 的診斷知識腳本中描述了如何根據SBKJ、SBGJ、QBF、QZF 等上行指令確定當前參數所屬設備的運行狀態,再根據不同的狀態得出正常值域的范圍(所述值域與遙測參數A002 相關)。

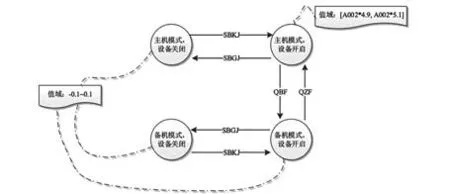
圖2 遙測參數A001 的診斷知識示意圖Fig.2 Schematic diagram of diagnostic knowledge of the telemetry data A001

由圖2 可知,遙測參數A001 的診斷知識腳本中出現了相關指令和遙測參數A002。由于對所有的下行遙測參數均可以書寫對應的故障診斷知識腳本,因此診斷知識中存在大量的不同下行遙測參數間的依賴關系。

2.2 循環依賴缺陷

在圖2 所示遙測參數A001 的診斷知識中,其值域與參數A002 相關。若參數A002 的診斷知識如圖3 所示,即參數A002 的狀態切換過程與遙測參數A001 一致,其值域與參數A001 相關。由于參數A001 的值域也與參數A002 相關,這樣就構成了一組循環依賴的診斷知識。顯然出現循環依賴的參數A001 的診斷知識和參數A002的診斷知識是不完備的,因為若在設備開啟且主機模式下這2 個遙測參數同時異常,但其遙測值依然滿足大于4.9 且小于5.1 的比值關系,則故障診斷系統并不會診斷出異常。

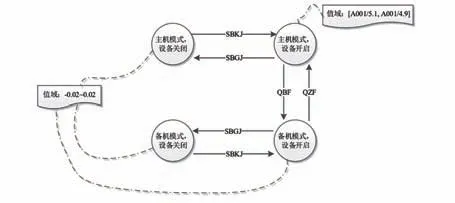
圖3 遙測參數A002 的診斷知識示意圖Fig.3 Schematic diagram of diagnostic knowledge of the telemetry data A002

即使對遙測參數A002 的診斷知識按圖4 所示進行加強改進,即當參數A002 遙測值＜2 時,可以診斷出異常。但通過分析可知,其與參數A001之間的比值關系判斷是冗余的,因為在參數A001的診斷知識中已經進行了該比值關系的判斷。

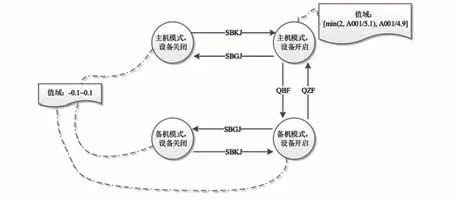
圖4 改進后的遙測參數A002 診斷知識示意圖Fig.4 Schematic diagram of improved diagnostic knowledge of the telemetry data A002

因此,若不同遙測參數的診斷知識中出現了循環依賴,一般而言意味著出現如下診斷知識缺陷:①故障診斷知識中可能存在不完備的表述;②故障診斷知識中可能存在冗余。

3 有向圖模型及經典圖算法

3.1 有向圖模型構建

有向圖D是指一個二元組(V(D),E(D)),其中V(D)表示頂點的集合,E(D)表示有向邊集合;在有向圖D中,E(D)中的每一個元素(即1 個有向邊)對應于V(D)中的1 對有序元素(即2 個頂點)e=(x,y),其中x為1 個有向邊的起點,y為這個有向邊的終點;此外,用頂點出度表示起點為該頂點的有向邊的數量,用頂點入度表示終點為該頂點的有向邊的數量[20]。本文所述的有向圖D不考慮2 個頂點之間存在多個有向邊的情況,即有向圖D為有向簡單圖。

當至少存在1 條路徑可以由頂點xs到頂點xe,則稱頂點xs至頂點xe可達。若有向圖D中存在2 個頂點相互可達,則稱有向圖D中存在環。而若一個有向圖D中的任意2 個頂點相互可達,則稱有向圖D是強連通(Strongly Connected);有向圖D的極大強連通子圖稱為有向圖D的強連通分量(Strongly Connected Components, SCC)。

針對本文所述航天器下行數據故障診斷系統中的診斷知識庫,構建有向圖Df= (Vf(D),Ef(D)),其中Vf(D)中的每個頂點對應1 個獨立的遙測參數,而Ef(D)中的每一個有向邊則表示其起點對應遙測參數的診斷知識與該有向邊終點對應的遙測參數相關。

至此,遙測參數故障診斷知識中的循環依賴檢測問題,就可抽象為有向圖Df中的環搜索問題。對于本文構建的有向圖Df,所有故障診斷知識中的循環依賴都對應于有向圖Df中的環,且這些環都存在于有向圖Df的SCC 中。

3.2 經典算法

3.2.1 拓撲排序算法

當拓撲排序算法[21]應用于診斷知識的循環依賴檢測問題時,其運算步驟如下:

1)根據Vf(D)和Ef(D),統計出Df中所有頂點的入度,記錄在列表List(Vf(D))中,此列表的元素個數為Vf(D)中的頂點個數,且每個元素中有對應頂點的入度信息。

2)掃描List(Vf(D))中所有入度為0 的元素,對于每個入度為0 的元素l,找到其對應的頂點x,并根據Ef(D)找出所有起點為x的有向邊e,將所有e指向的終點對應的List(Vf(D))中元素的入度減去1;從List(Vf(D))中刪除元素l。

3)反復執行步驟2,若列表List(Vf(D))已空,或者執行步驟2 后的列表List(Vf(D))與執行前相同,則執行步驟4。

4)若列表List(Vf(D))為空,則診斷知識中不存在循環依賴;否則List(Vf(D))中的每個元素所對應的遙測參數都處于循環依賴中。

上述拓撲排序檢測算法通過執行1 次廣度優先搜索,即可得出診斷知識中是否存在循環依賴的結論,其算法的時間復雜度為O(V+E),其中V代表Vf(D)中的頂點數目,而E代表Ef(D)中的有向邊數目。

3.2.2 Kosaraju 算法

Kosaraju 算法[22]通過正反2 次深度優先搜索過程確定有向圖中的SCC,也可以用于診斷知識的循環依賴檢測,運算步驟如下:

1)對有向圖Df中的所有頂點Vf(D),根據Ef(D)以后序深度優先搜索方式進行遍歷入棧(棧Stack),所述后序深度優先是指先遞歸訪問起點為當前頂點的有向邊指向的終點,再入棧當前頂點;記錄每個頂點的入棧時間。

2)將Ef(D)中的每個有向邊反序,得到反序有向圖D′f=(Vf(D),E′f(D))。

3)將Stack 中棧頂的頂點出棧,若該頂點已被步驟3 處理過,則執行步驟4;若該頂點未被步驟3 處理過,則由該頂點在反序有向圖D′f中對應的頂點開始,根據E′f(D)進行深度優先搜索,記錄由該頂點能夠遍歷到的所有頂點,這些頂點就構成了有向圖Df的一個SCC,并標記這些頂點已被步驟3 處理過。

4)若Stack 已空,則算法結束;否則,繼續步驟3。

Kosaraju 算法通過執行2 次深度優先搜索,可以得出有向圖Df中的所有SCC,其算法的時間復雜度也為O(V+E)。

3.2.3 Tarjan 算法

Tarjan 算法[23]可以僅通過1 次深度優先搜索過程就確定有向圖中的SCC,從而實現診斷知識的循環依賴檢測。與Kosaraju 算法類似,Tarjan算法對圖Df中的所有頂點Vf(D),根據Ef(D)以先序深度優先搜索方式進行遍歷入棧,所述先序深度優先是指先訪問當前頂點,再遞歸訪問起點為當前頂點的有向邊指向的終點,每次訪問時執行如下步驟:

1)訪問頂點時首先記錄1 個該頂點的入棧時間,并初始化另一個稱為可達最小入棧時間的值為同一時間;在Ef(D)中找出所有以該頂點為起點的有向邊,對于每個有向邊(x,y)執行步驟2;隨后判斷,若該頂點的入棧時間與可達最小入棧時間相同,則執行步驟3。

2)若y對應的頂點尚未入棧,則對y執行步驟1,并將x的可達最小入棧時間更新為x的可達最小入棧時間和y的可達最小入棧時間中的較小值;若y對應的頂點已入棧,則將x的可達最小入棧時間更新為x的可達最小入棧時間和y的入棧時間中的較小值。

3)執行出棧操作,直至步驟1 的當前訪問頂點出棧,這些頂點構成有向圖Df的1 個SCC。

Tarjan 算法僅通過1 次深度優先搜索,即可得出有向圖Df的中的所有SCC,其算法的時間復雜度也為O(V+E)。

3.3 改進算法

引入圖論模型后,可以應用上述拓撲排序、Kosaraju、Tarjan 等經典算法來檢測故障診斷知識中的循環依賴缺陷,但考慮到航天器下行數據故障診斷系統的診斷知識會經常迭代,為了在迭代時提示用戶所更新的診斷知識是否存在循環依賴的缺陷,就需要在每次診斷知識迭代時開展缺陷檢測,這個檢測過程會引入較大的運算量,對于中國空間站這種復雜航天器,該檢測過程的運算量將更加龐大,甚至會影響知識更新的實時性。因此,本文在分析故障診斷知識迭代特點的基礎上,提出了一種改進Tarjan 算法,以降低循環依賴缺陷檢測的運算量。

3.3.1 故障診斷知識的迭代由于故障診斷知識的迭代是以各遙測參數為單位進行的,用戶往往針對某個特定的少量遙測參數進行診斷知識的更新,而無需對所有的遙測參數進行故障診斷知識迭代。若可以在對所有遙測參數的診斷知識進行全范圍循環依賴缺陷檢測前,對一些無需進行全范圍搜索即可得出結論的情況進行過濾,就可以極大降低系統的開銷。

3.3.2 改進Tarjan 算法

改進Tarjan 算法的核心思想是首先判斷某次診斷知識的迭代更新是否改變了有向圖Df的SCC 特性,如不改變,則不再進行診斷知識的缺陷檢測;同時在每次全范圍搜索后,保留各SCC 的記錄,并優先檢測所迭代遙測參數所屬的SCC 是否依然全連通,從而降低進行全范圍搜索的可能性。

具體算法如下:

1)初始化時,對有向圖Df利用Tarjan 算法搜索得到所有SCC,并記錄其中頂點數量≥2 的部分,記錄為Qf;

2)當1 個遙測參數的診斷知識更新時,若其舊版診斷知識已檢測出存在循環依賴缺陷,則執行步驟3,否則執行步驟5;

3)比對新版診斷知識與舊版診斷知識中相關遙測參數的范圍,若范圍增大或者保持不變,則提示依然存在循環依賴缺陷,否則執行步驟4;

4)在遙測參數所屬SCC 中,再次進行小范圍的Tarjan 算法,若依然保持全連通性,則直接提示依然存在循環依賴缺陷,否則執行步驟6;

5)比對新版診斷知識與舊版診斷知識中相關遙測參數的范圍,若范圍縮小或者保持不變,則提示正常,否則執行步驟6;

6)對有向圖Df利用Tarjan 算法重新搜索1 次所有SCC,并將其中頂點數量≥2 的部分更新為Qf,若本遙測參數對應的頂點在更新后的Qf中,則提示存在循環依賴缺陷,否則提示正常。

由上述步驟可知,改進Tarjan 算法并未影響單次Tarjan 執行過程,而是通過步驟3 和步驟5來避免后續較為復雜的Tarjan 執行過程,從而達到降低運算量的目的。

4 算法對比及驗證

4.1 算法對比

拓撲排序算法、Kosaraju 算法和Tarjan 算法都 以O(V+E)的時間復雜度判斷有向圖Df中是否存在環,但Kosaraju 算法和Tarjan 算法還可以得出Df中的所有SCC,這在實際的診斷知識缺陷檢測中十分有用,可提示用戶進行針對性調整。在不考慮空間復雜度時,由于Tarjan 算法僅需進行1 次深度優先搜索,而Kosaraju 算法則需要進行2 次深度優先搜索,因此Tarjan 算法的執行效率優于Kosaraju 算法。

綜合對比后,Tarjan 算法在診斷知識的循環依賴檢測中的綜合表現更優;而本文提出的改進Tarjan 算法可以有效減少具體執行Tarjan 過程的次數,帶來更低的運算開銷。

4.2 仿真結果

構造包含500 000 個頂點的有向圖,其中分別有6‰、12‰、18‰、24‰、30‰、36‰、42‰、48‰、54‰和60‰的頂點存在循環依賴問題,仿真200 次,其中本文提出的改進Tarjan 算法有1%的可能僅執行步驟3 或步驟5 即可得出結論,則各算法執行時間的對比圖如圖5 所示。

由圖5 可知,拓撲排序算法的耗時最少,但是由于其無法得出Df中的所有SCC,因此無法在實際工作中實際應用;Tarjan 算法耗時優于Kosaraju算法,而本文提出的改進Tarjan 算法較Tarjan 算法更優,且循環依賴越嚴重,降低運算開銷效果越明顯。

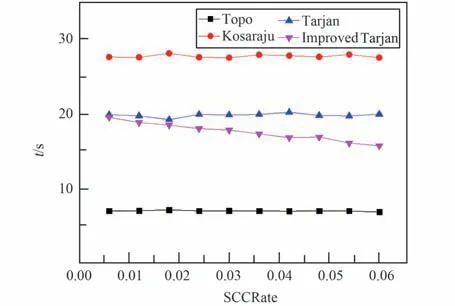
圖5 不同算法執行時間對比Fig.5 Comparison of execution time of various algorithms

4.3 改進Tarjan 算法的執行效果驗證

將改進Tarjan 算法實際應用于某型號,統計一段時間內僅執行步驟3 或步驟5(無需執行步驟4 和步驟6)即可得出結論的次數,計算得到這些次數相對于總診斷知識迭代次數的比率,如表1 所示。

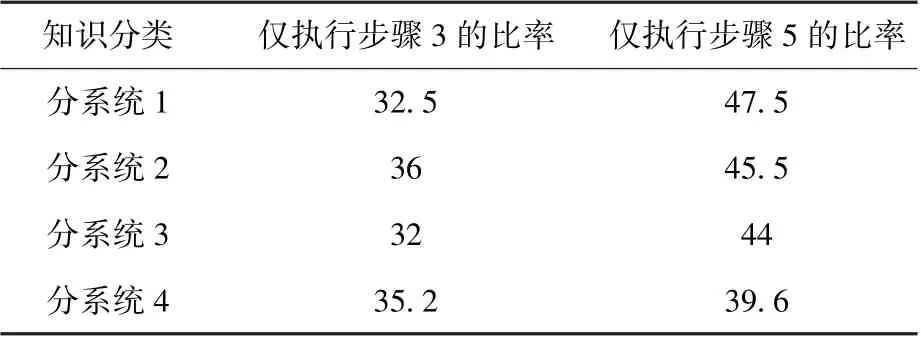
表1改進Tarjan算法僅執行步驟3或5的比例Table 1Therateofstep3onlyandstep5onlyofthe improvedTarjanalgorithm單位:%

如表1 所示,改進Tarjan 算法在實際運行中避免了70%以上的全范圍或小范圍Tarjan 搜索過程,從而大幅降低了系統的計算開銷。

5 結論

航天器下行數據故障診斷系統作為專家系統的一種典型實現,存在知識獲取瓶頸。經過分析,一類典型的診斷知識缺陷是不同遙測參數的診斷知識中存在循環依賴。本文通過將診斷知識中的循環依賴檢測問題抽象為有向圖中的環搜索問題,從而得以應用經典的拓撲排序算法、Kosaraju算法和Tarjan 算法開展診斷知識的缺陷檢測,并結合診斷知識經常迭代更新的特點,提出了一種改進Tarjan 算法。

1)將拓撲排序、Kosaraju 算法、Tarjan 算法等經典算法引入問題解決過程,對比發現了Tarjan算法的優勢;

2)考慮到診斷知識的迭代以單個遙測參數為單位進行,在Tarjan 算法執行前,對無需執行Tarjan 核心步驟即可得出檢測結論的部分進行過濾,設計的改進Tarjan 算法在有效檢測診斷知識的循環依賴缺陷的同時,可大幅降低了系統的運算開銷。