圓錐曲線離心率問題之“一題多解”

■江蘇省沙溪高級中學 邵敏亞 魏志英

圓錐曲線離心率問題,歷來是各級各類考試的命題重點,由于這類問題方法靈活,綜合性較強,因而也是同學們學習的難點。那么這類問題該如何破解呢? 同學們或許能從下面幾個例題的“一題多解”中得到啟示。

一、求離心率的值

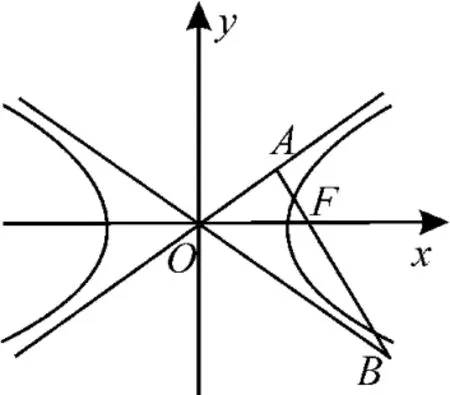
圖1

(法4)如圖2,過點F向雙曲線的另一條漸近線作垂線,垂足為D,則|DF|=b,|BF|=2b。

圖2

法3首先將∠AOF與∠AOB的正切值用a,b表示,再利用正切二倍角公式得到a,b之間的關系式,進而求出離心率的值。此法利用了雙曲線焦點到漸近線的距離為b的特征,結合圖形,巧妙地利用了長度關系及雙曲線的對稱性。解題過程中體現了數形結合思想與方程思想,對大家的觀察能力及分析問題的能力有較高的要求。

法4 則通過添加輔助線,將“|AF|與|BF|”化到同一個直角三角形中,利用|AF|與|BF|的長度關系及相似、雙曲線漸近線的對稱性得到∠AOF的大小,進而求出離心率,構思巧妙,易于運算。本法與法3 類似,但優于法3,體現了數形結合思想的妙用。

二、求離心率的取值范圍

圖3

點評:求圓錐曲線離心率的取值方法一般采用不等式法和函數值域法。

法1利用橢圓的對稱性,將|BF|轉化為|AF′|,將|AF|與|AF′|用角θ表示,再利用橢圓的定義將離心率e表示為θ的函數,將離心率e的取值范圍問題轉化為三角函數的值域問題,求解時應特別注意角θ的取值范圍。本法體現了函數思想的應用。

法2將點A的坐標用角θ表示,然后代入橢圓方程解出cos22θ。利用求出cos22θ的取值范圍,得到關于e2的不等式,結合0＜e＜1 得出e的取值范圍。法2利用了點在曲線上,即點的坐標滿足曲線方程的特征,解題過程中體現了方程思想與化歸思想,對大家的運算能力及化歸能力有較高的要求,而利用余弦函數的有界性將問題轉化為不等式問題是解題的關鍵。

法3將m,n用θ表示,利用橢圓的定義及△AFF′是直角三角形,將e表示為tanθ的函數,利用對勾函數求解。本解法與法1類似,只是對的處理上有所不同。這里利用化切處理再結合均值不等式得解,體現了函數思想與化歸思想,在數和式的處理上對我們提出了較高的要求。

法4則利用極端情況,即∠AOx=時的情況,將|OA|2的長度用a,b表示,再結合|OA0|≤|OA|=c得到事實上這里也可用余弦定理及勾股定理將|AF|,|AF′|用c表示,再結合橢圓定義得解。法4采用“以靜制動”的方式處理問題,要求同學們具有較好的觀察能力與推理能力。

法5利用S△AFB=S△AFF′,結合焦點三角形面積公式將表示,再利用sin 2θ的有界性求出e的取值范圍。本解法與法2類似,利用了正弦函數的有界性,同樣要求大家具有較好的分析、解決問題的能力和豐富的函數不等式的知識儲備。

三、離心率之間的關系

例3已知橢圓C1與雙曲線C2有相同的焦點F1,F2,曲線C1,C2的一個交點為P,且PF1⊥PF2,則橢圓C1的離心率e1與雙曲線C2的離心率e2一定滿足的關系是( )。

圖4

點評:本例是個選擇題,求解時不僅要用到圓錐曲線的有關定義和幾何圖形的特征,還可采用特殊化法。從而達到快速解答的目的。

本例法1取特例,對選項進行檢驗排除,可以快速地得到答案。作為選擇題,如果能用特例進行排除,可以提高準確率。本解法體現了特殊化方法的優勢。

法2 是求解圓錐曲線離心率的常用方法,利用圓錐曲線定義結合平面幾何知識,從幾何關系尋求a,c的關系式。分析圖形的幾何特征,利用幾何關系建立關于a,b,c的方程是解決離心率問題的常見策略。法2體現了方程思想的運用,對代數式的恒等變形能力要求較高。

法3利用橢圓與雙曲線焦點三角形的面積公式,得到曲線之間的關系。橢圓焦點三角形面積(其中θ=∠F1PF2),法3體現了方程思想與化歸思想的運用,要求我們具有較好的分析、解決問題的能力。

法4最為簡捷,但要求我們善于運用代數式的恒等變形,具有較高的數學運算素養。