基于三維點云的卷積運算綜述

韓 冰 張鑫云 任 爽

（北京交通大學計算機與信息技術學院 北京 100044）

（bhan0458@bjtu.edu.cn）

3D 傳感器（如激光雷達和深度相機）的普及引起了人們對3D 視覺的廣泛關注，這些傳感器采集的3D 數據可以提供豐富的幾何結構和尺度細節，這也在許多領域得到了實際應用，包括自動駕駛技術[1]、機器人控制技術[2]等.3D 數據通常可以用不同的格式來表示，包括深度圖（depth map）、網格（mesh）、體素（voxel）、點云（point cloud）、點云序列（point cloud sequence）等[3]，這些數據之間可以相互轉換.在這些表示中，點云是最靈活的且最常用的，因為它們完整保留了物體在3D 空間中最原始的幾何信息，可以從以上3D 傳感器中直接獲取或從各種3D 建模軟件中直接導出.然而，由于點云數據中各個點分布的不均衡性和表示的不規則性，處理點云仍然是一項有挑戰性的任務.

近年來，深度學習技術逐漸成為各個領域的研究熱點.PointNet[4]及其變體PointNet++[5]等方法的提出，解決了深度學習處理不規則數據格式的難題，也促使數據驅動的深度學習方法在點云上的研究不斷地深入.但由于PointNet[4]利用共享多層感知機（multilayer perceptron,MLP）直接處理點云中的單個點，并通過最大池化（max pooling）操作來聚合各個點的所有信息，未能考慮點之間的相關性并進行充分利用，這也就導致了學習到的目標物體的特征存在著結構信息和局部細節的缺失.卷積神經網絡（convolutional neural network,CNN）作為一種標準的深度學習體系結構，由于其出色的局部信息聚合能力而被越來越多地采用，同時利用它的平移不變性和局部相關性，在機器視覺領域處理規則排列數據（如2D 圖像、視頻）方面的研究中已經取得了一系列突破，極大地改進了幾乎每項視覺任務的結果（如識別[6]、檢測[7]、分類[8]、分割[9-10]等）.執行卷積運算的目的是從輸入數據中提取出有用的特征進行學習.與深度神經網絡（deep neural network,DNN）相比，卷積神經網絡中的卷積運算減少了網絡的訓練參數量，提高了網絡的泛化能力.因此，許多研究嘗試將2D 卷積網絡直接擴展到3D 空間，以使得卷積運算能夠分析處理3D點云數據.

對比點云與圖像之間的差異示例如圖1 所示.圖像的像素（pixels）通常可以表示為規則的網格矩陣.在每個局部區域內，不同像素之間的相對位置是固定的，如圖1（a）所示.而點云是3D 空間中對目標物體進行曲面采樣得到的一組點的集合，即P={pi|i=1,2,…,n}，其中每個點pi默認包含1 個位置信息，即3D 坐標（XYZ），有時可能還包括顏色（RGB）信息或法線（normal）信息.類似地，對比點云序列與視頻之間的差異示例如圖2 所示.視頻可以看作連續的多幀圖像的集合，點云序列可以看作連續的多幀點云的集合.與圖像相比，視頻中增加了時序上下文關系（temporal context）.將其推廣到3D 空間，與點云相比，點云序列中同樣增加了時序上下文關系.因此，在進行以視頻為輸入數據的2D 目標跟蹤任務和以點云序列為輸入數據的3D 目標跟蹤任務時，需要充分利用這一關系以處理連續幀之間的冗余，解決模糊失焦、部分遮擋等問題.

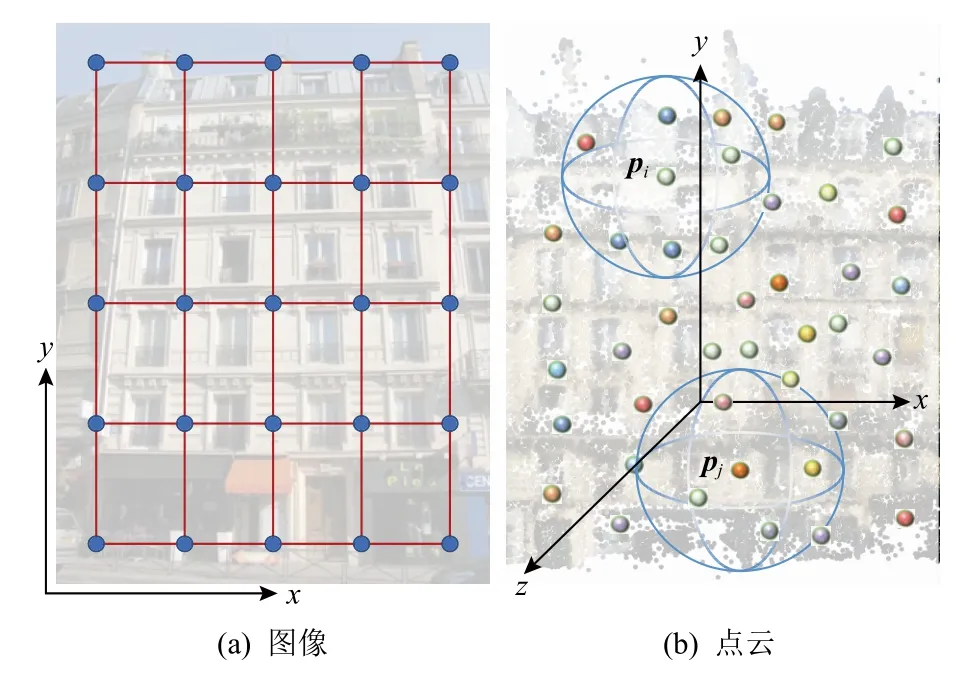
Fig.1 Comparison of images and point clouds圖1 圖像與點云的對比

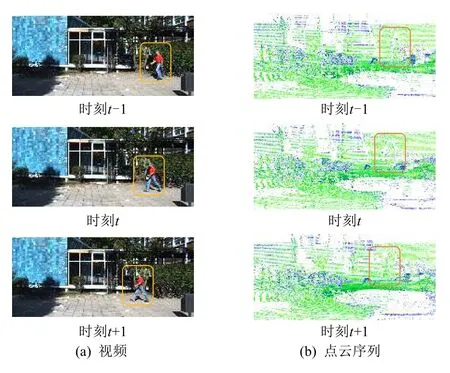
Fig.2 Comparison of video and point cloud sequence圖2 視頻與點云序列的對比

與圖像/視頻不同，點云更加靈活且無規則，點的坐標不一定位于固定網格上，即每個局部區域中所包含的不同點之間的相對位置都是不同的，如圖1（b）所示，以為中心的鄰域和以R3為中心的鄰域中各個近鄰點的位置和個數是不同的，對應目標物體的形狀也不同.因此，在圖像/視頻上使用的傳統卷積運算不能直接應用于點云/點云序列.

綜上所述，阻礙采用標準卷積運算學習3D 點云特征的原因一般有3 個：

1）點云是由無序的、不規則的點構成的集合，卷積運算應對點的輸入順序具有排列不變性（permutation invariance），即使輸入點的順序不同，學習之后也能得出相同的結果.

2）點云分布在3D 幾何空間中，卷積運算應對點云的剛性變換具有魯棒性，包括旋轉不變性（rotation invariance）、平移不變性（translation invariance）和尺度不變性（scale invariance）.

3）點云具有潛在的幾何形狀，卷積運算學習得到的點云形狀應具備可區分性，防止丟失局部形狀信息.

因此，針對這3 方面的原因，為了學習3D 點云的基本形狀和幾何結構，現有的研究主要分成了2種策略：一種策略是將3D 點云轉化為可以直接進行2D 或3D 標準卷積運算的結構；另一種策略是構造可以直接處理點云的卷積算子.首先，點云轉化為其他結構的方法如圖3 所示，主要包括4 個方法：

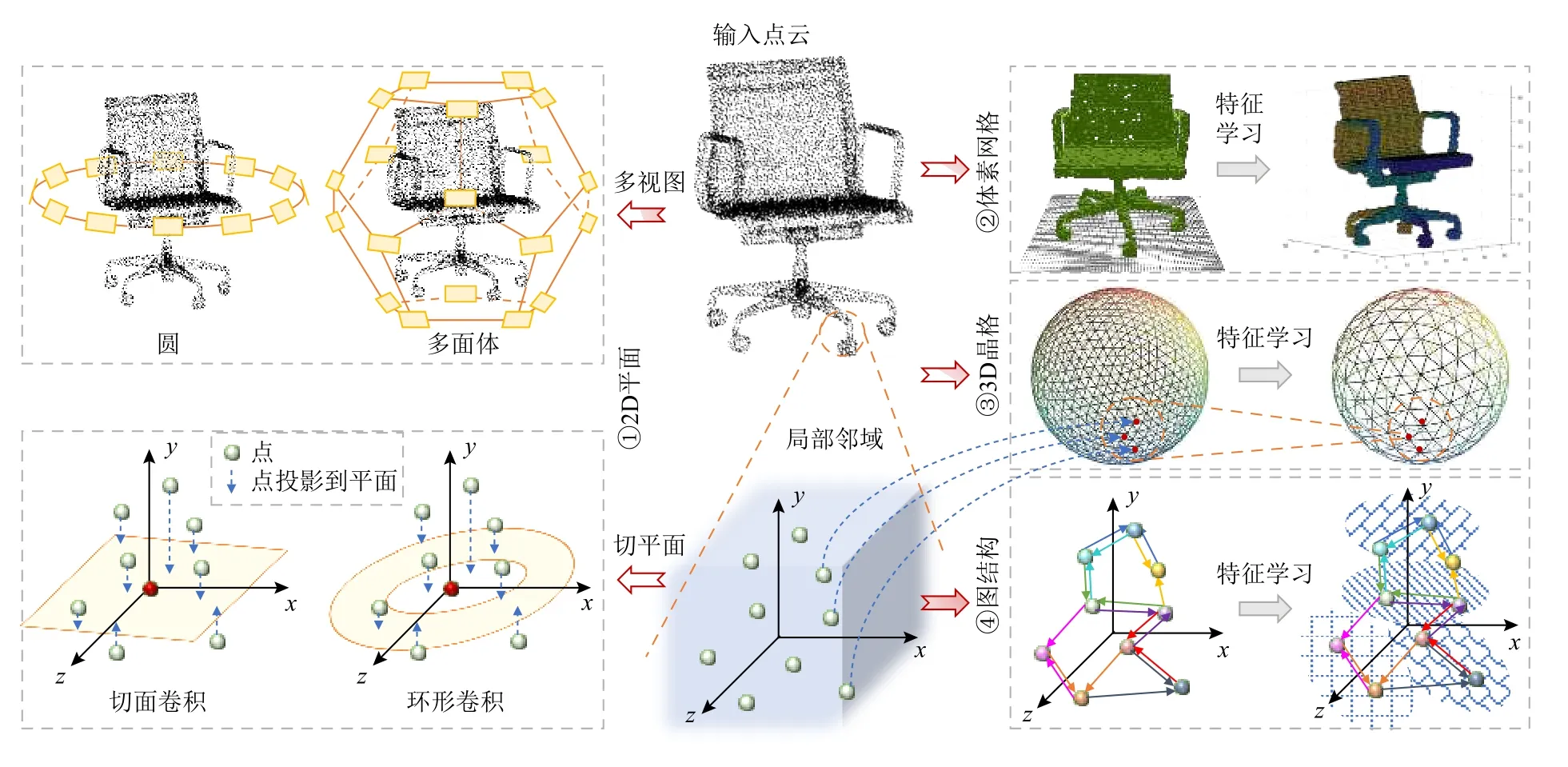
Fig.3 Transformation methods of 3D point clouds圖3 3D 點云的轉化方法

1）基于投影的方法（projection-based method）.如圖3 中的①所示，將3D 點云投影到2D 平面上，例如多視圖[11-14]、切平面[15-17].然而由于掃描設備生成的原始點云數據存在自遮擋（self-occlusion）或密度不均勻等問題，在投影過程中不可避免地會損失一些3D 幾何形狀的深度信息和結構信息，同時在處理一些稀疏點云數據時通常效率低下且耗時.將點云投影為多視圖還會因為不同視圖之間的不連續性導致在細節敏感的任務（如部件分割）上的性能較差；將點云投影在切平面時依賴于對切平面的正確估計，此外還需要一些額外的輔助信息，即法線，然而許多像激光雷達等傳感器生成的點云數據都不具備這樣的信息.

2）基于體素的方法（voxel-based method）.如圖3中的②所示，將物體的幾何形式表示（如點云）體素化（voxelization）為最接近該物體的3D 體素網格[11,18-24].雖然這種方法易于實現，但由于點云分布的不均勻性，如何進行適當地體素化是關鍵.表示點云的體素與表示圖像的像素類似，后者是像素點，而前者擴展到了立方體單元.這個立方體單元的大小與空間分辨率有關，體素網格劃分越精細，立方體單元越小，空間分辨率越高，但計算復雜度和內存占用會隨著細化程度呈立方級增長；反之，體素網格劃分越粗糙，立方體單元越大，空間分辨率越低，計算復雜度和內存占用就越低，但分辨率不足會導致物體的一些局部細粒度幾何細節的丟失，通常還會存在大量不包含點的空體素網格導致計算結果的偏差和內存空間的無效占用.

3）基于晶格的方法（lattice-based method）.如圖3中的③所示，將點云投影到規則的晶格空間，例如正多面體晶格（permutohedral lattice）[25]、球形晶格（spherical lattice）[26].這種方法可以解決點云的部分位置稀疏性問題，但類似于體素網格，通常也需要消耗大量內存來存儲晶格特征，且在高分辨率要求下計算復雜度將會大大增加.其次，投影到某個規則晶格空間中，很有可能不再保留這些點之前在原始歐氏空間中所具備的幾何信息.

4）基于圖的方法（graph-based method）.如圖3 中的④所示，將3D 點云構造為圖結構，點云中的各個點作為圖的頂點，點與其鄰域內的部分近鄰點形成有向邊，進而借助于圖卷積網絡（graph convolution network,GCN），在譜域（spectral domain）[27-31]或空間域（spatial domain）[32-43]中學習特征.這些方法能夠直接處理不規則的數據結構，但也存在一些缺點，例如，局部圖的構造不是稀疏不變的.從同一物體表面采樣的不同密度點云會得到不同的鄰域，從而可能產生不同的圖構造結果.同時，在構建鄰域時，可能會忽略法線方向，從而導致局部幾何信息的丟失.這些對不規則輸入數據的轉化方法均會在一定程度上導致物體的幾何信息的丟失，并且這些轉化操作會導致計算復雜度和內存消耗的急劇增加.

鑒于此，越來越多的研究人員致力于研究基于點的方法（point-based method），構造各種各樣的卷積運算及卷積網絡來學習點及其鄰域內的其他點的特征，直接在原始點云數據上進行分析，可以在處理不規則的點云任務上實現優異的性能.為了能夠充分利用數據的空間局部相關性，卷積運算中使用的卷積算子也成為了提高點云分析的算法性能和結果準確性的重要影響因素.因此本文重點關注點卷積算子（point convolution operator）及其對應的網絡結構，這類卷積運算可以直接處理原始點云，而不進行任何轉化，不需要任何中間表示，也因此不會引入其他的信息損失.

目前國內外關于點云的相關綜述有很多，文獻[3]涵蓋了不同的應用，按照形狀分類、目標檢測與跟蹤、點云分割3 大任務進行劃分，對應用在點云的深度學習方法的最新進展進行了全面綜述和詳細展開，涉及的方面較為廣泛.文獻[44]將現有的點云特征學習方法分為基于點的特征學習和基于樹的特征學習，并通過具體任務的應用來分析這些方法的優缺點.文獻[45]通過分析點云應用中面臨的挑戰和深度學習的優勢，詳細展開分析了幾種經典的直接處理點云的深度學習方法.文獻[46]系統回顧并詳細介紹了自動駕駛應用領域中的激光雷達點云的特定任務.此外，還有一些綜述側重于對點云的具體任務的基礎原理及關鍵技術進行分類、分析與總結，例如，點云法向量估計任務[47]、點云場景分割任務[48]、點云語義分割任務[49-51]、點云配準任務[52]、點云序列的點態預測任務[53]等.

1 標準卷積

卷積神經網絡，最早是由LeCun 等人[6]提出并應用在手寫字體識別與分類任務中，稱為LeNet-5.在過去的幾年中，2D 卷積的應用最為廣泛且研究相對成熟，最大的原因是圖像的規則像素可以很容易地通過權重共享（weight sharing）和平移不變（translation invariance）特性進行相應的卷積運算.此外，還可以通過改變卷積核的構造，如空洞卷積（dilated/atrous convolution）、可分離卷積（separable convolution）、組卷積（group convolution）等，使得卷積網絡能夠根據多尺度層次結構上的感受野（receptive field）來學習和豐富特征.與2D 卷積不同，3D 卷積在問題上并沒有達到相同水平的研究進展，這是由于其在建模和訓練中存在著一些障礙，如計算復雜度較高；內存占用較大；存在大量待學習參數，容易產生過擬合，因此需要對網絡架構或卷積運算進行改進來提升特征學習能力.

本節將回顧這些標準卷積運算的原理，以幫助理解與第2 節的點云卷積運算之間的區別與聯系，為后續各種處理不規則3D 點云數據的卷積運算的深入研究奠定基礎.

標準卷積運算是指卷積算子以滑動窗口的方式在局部區域上的點集合或者特征集合進行加權求和得到輸出結果的過程，這一過程能夠從若干相關特征中以特定的方式提取新的特征.卷積實際上是一種積分運算，相應的離散卷積和連續卷積的一般定義分別為：

1）離散卷積（卷積算子定義在離散空間）.

其中卷積算子g:S →R和特征f:G→R分別是定義域S=ZD和G=ZD上的函數.

2）連續卷積（卷積算子定義在連續空間）.

其中卷積算子g:S →R和特征f:G→R分別是定義域S=RD和G=RD上的連續函數.

2D 卷積運算是指卷積算子即如圖4（a）所示尺寸為[width,height]的卷積核（kernel）在寬度和高度2個維度上的滑動并計算，此時D=2.而3D 卷積是指卷積算子即如圖4（b）所示尺寸為[width,height,depth]的濾波器在寬度、高度、深度的3 個維度上的滑動并計算，此時D=3.

2 基于點的卷積

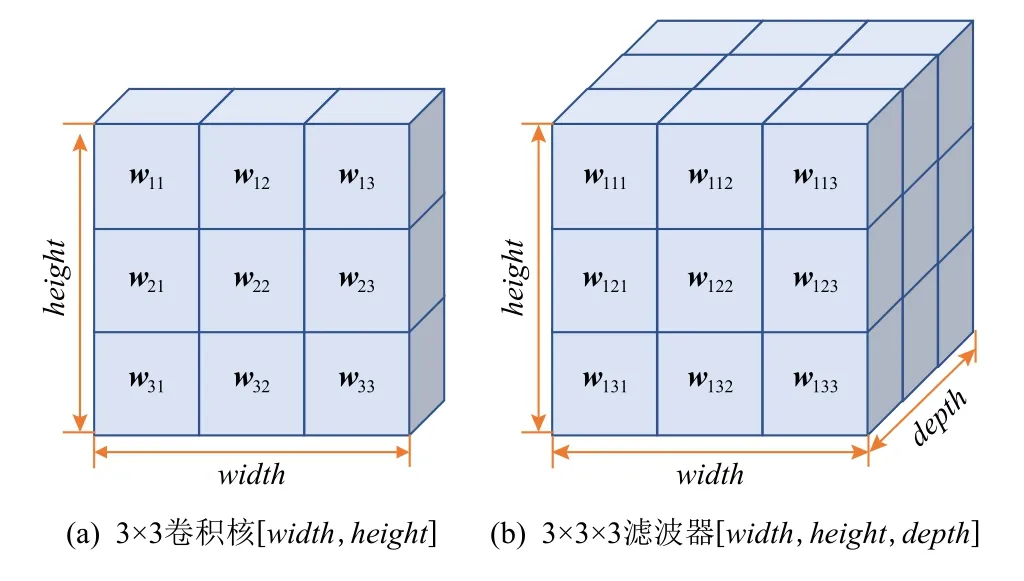
Fig.4 Illustration of 2D and 3D convolution operators圖4 二維和三維卷積算子示意圖

標準卷積網絡的成功應用表明，保持卷積運算的穩定性是必不可少的，即鄰域大小不變和鄰居個數不變.然而由于點云中的點排列不規則、點密度不均勻，這種穩定性屬性在點云數據中是不存在的，無法始終同時保持區域大小不變（例如，半徑為R的局部鄰域）和鄰居個數不變（例如，K個近鄰點）.這使得標準卷積難以處理此類數據.為了克服這一問題，越來越多研究人員致力于提出有效的直接作用于點云的卷積算子，如圖4 所示，這些算子大多是即插即用（plug-and-play,PnP）的，可以很容易地集成到各種3D 點云分析任務（如分類、分割）的流程（pipeline）中去，詳見第3 節.因此，可以總結出利用卷積網絡在點云上進行有效學習主要有3 個關鍵要求：

1）定義輸入點集，該點集可以是整個點云的集合，也可以是點云的子集.前者需要描述整個點云的全局特征向量；后者為每個點集尋找一個局部特征向量，在學習全局特征時可以進一步組合.

2）構造一個能夠在點云上使用的卷積算子，該算子能夠有效解決點云的排列不變性和密度不均勻性，并且可以學習點之間的局部幾何特征.

3）構造一個能夠集成卷積算子的卷積神經網絡，該網絡結構可以從輸入點云中逐步提取局部（local）到全局（global）的深層次語義信息，輔助點云任務更好地完成.pi∈RD

首先，類似于標準卷積，可以將基于點的卷積定義為

其中 ⊙是特征函數f:RD→RF和權重函數g:RD→RF之間的哈達瑪積（Hadamardproduct），特征函數f是為每個絕對位置pj∈RD分配一個特征向量權重函數g是為每個相對位置pi?pj∈RD映射一個權重向量使用蒙特卡洛積分（Monte Carlo integration），可以進一步將卷積運算近似為對含有N個點的點云操作

為了更準確有效地提取高維特征和局部細粒度信息，在2D 圖像卷積中，通過如圖4（a）所示的3×3或5×5 的像素核來定義局部鄰域范圍.類似地，對于點卷積，通過在每個點周圍定義局部鄰域和近鄰點集合來實現

其中 Nt是點pi的局部鄰域內的近鄰點集，pk是pi的第k個近鄰點.這也就滿足了關鍵要求1）.

其次，針對關鍵要求2），點云卷積性能取決于卷積算子中權重函數w的學習和更新.因此，可以根據權重函數的類型，將現有的基于點云的卷積方法分為離散卷積和連續卷積，如圖5 所示.離散卷積方法中的卷積權重與近鄰點和中心點之間的偏移量（相對位置）有關，通常根據距離等特征為落入同一個局部區域的所有點分配相應的權重.而連續卷積方法中的卷積權重與近鄰點相對于中心點的空間分布有關，通常根據近鄰點的空間分布為每個點分配權重.

Fig.5 Local neighborhood centered on point pi and its corresponding discrete convolution and continuous convolution圖5 以點pi 為中心的局部鄰域及其對應的離散卷積和連續卷積

顯然，在進行卷積之前，大多研究都會首先采樣得到中心點集，然后尋找每個中心點的局部鄰域及其近鄰點集 Ni.目前使用最廣泛的采樣中心點的方法主要有隨機點采樣（random point sampling,RPS）、最遠點采樣（farthest point sampling,FPS），后者相對于前者的優勢在于它可以盡可能地覆蓋空間中的所有點，找到一些有代表的點，而前者的時間復雜度相對較低[54].關于尋找某個點的局部鄰域的策略，目前在點云研究中使用最廣泛的除了圖5（a）所示的球查詢（ball query）算法外，還有K近鄰（Knearest neighbor,KNN）算法，二者的區別是前者指定鄰域范圍，選擇在以中心點為球心、以R為半徑的球形區域內的點作為該中心點的近鄰點，組成的集合即為 Nt；而后者指定近鄰點數，尋找與中心點距離最近的K個點作為該中心點的近鄰點.有研究表明二者的選擇對實際點云任務的性能影響相差不大[40].在之后的小節中，我們的重點是分析各研究工作所提出的卷積算子的設計原理及在此基礎上構建的卷積網絡.因此若研究工作中沒有涉及對點鄰域進行改進，則默認前提是通過球查詢算法和KNN 算法采樣得到的中心點及其近鄰點集.

2.1 離散卷積

在不規則點云上進行卷積運算的一個首要問題是，權重向量的空間位置通常與輸入點無法對齊.將點云體素化為規則網格解決了這一問題，但代價是丟失了局部幾何結構，這對于一些追求高性能的點云任務通常是不可取的.因此，在基于點的離散卷積中，一些研究首先想到通過解決點的排列不變性問題來處理這一問題，還有一些研究考慮了點的空間幾何特性.

2.1.1 排列不變性

為了解決點云的排列不變性，Hua 等人[55]通過指定點的輸入順序，提出了逐點卷積算子（pointwise convolution）.具體來說，將所有點按照指定順序（如3D 坐標x→y→z）依次輸入到逐點卷積神經網絡（pointwise CNN）中，以每個點為中心得到指定數量的近鄰點并將其劃分到對應的核單元（kernel cell），每個核單元內的所有點都具有相同的核權重，核的尺寸可以根據每個卷積層中不同數量的近鄰點進行適當地調整.類似地，Li 等人[56]提出了一個χ-Conv 卷積算子，關鍵在于將局部坐標系的原點定位在每個中心點，使得該算子不依賴于中心點及其近鄰點的絕對位置，而依賴于它們的相對位置，采用多層感知機根據相對位置學習一個χ-變換矩陣作為卷積核權重矩陣，與中心點特征及其近鄰點特征的結合矩陣進行卷積運算得到高維特征，將多個χ-Convs 進行級聯（concatenation）或跨層連接（skip connection）可以得到點卷積神經網絡（PointCNN）的多種結構從而來進行不同的點云任務.由于在一些實際場景中，物體的大小各不相同，為了使提取的特征適應不同大小的物體，即小物體具有較小范圍的鄰域特征，大物體具有較大范圍的鄰域特征，基于卷積算子χ-Conv 和網絡PointCNN[56]，Zhang 等人[57]提出了基于彩色植被指數的多尺度卷積神經網絡（multiscale CNN with color vegetation indices,MCCNN），利用顏色信息為原始點云數據中的每個點計算超綠（excess green,ExG）和超紅（excess red,ExR）這2 種彩色植被指數，并與其位置信息一起作為輸入特征，然后設置中心點的不同數量的近鄰點或者不同范圍的鄰域，得到不同的卷積核來提取多尺度特征，同時增強點云的可區分性.

2.1.2 點幾何特性

將點從歐氏空間映射到了其他空間，雖然解決了點云的排列不變性問題，但也因此損失了3D 物體的幾何信息.因此，為了在整個特征提取中保留歐氏空間的幾何結構信息，一些研究通過4 種方法來更充分地學習點之間的幾何信息，提升網絡的學習效率及性能，包括：建立點的方向向量；設計點的局部鄰域；改變點卷積的感受野；構建點與卷積權重的相關性.

1）建立點的方向向量[58-59]

Lan 等人[58]基于物體的幾何信息隱含在點云的坐標中這一合理的假設，提出了一種幾何卷積算子（geometric-induced convolution,Geo-Conv），如 圖6 所示，具體卷積運算過程包括：①特征分解（feature decomposition）.將中心點與其近鄰點所組成的邊向量分解到3 個正交坐標基上，沿著各個基底（base）獨立學習邊特征.②特征提取（feature extraction）.對中心點來說，通過與一個可學習的方向相關權重矩陣進行加權求和來提取該點在各個方向上的特征.③特征聚合（feature aggregation）.將提取到的特征與邊向量和正交基之間的夾角成比例地聚合得到點之間的幾何結構信息.通過逐層擴大卷積的感受野，將多個Geo-Convs 作用于不斷增大的局部鄰域以分層提取特征，構建一個幾何誘導卷積神經網絡（geometric-induced CNN,Geo-CNN），對局部區域點之間的幾何結構進行建模，最后通過一個最大池化層來聚集所有點的全局特征.然而網絡在每次卷積都需要重新計算所有點的近鄰點，使得其計算復雜度大大增加，不適合處理大規模場景.此外，除了物體內部點的幾何特征，邊界信息在一些點云分割任務中起著重要作用，當邊界信息被忽略時，提取的特征通常是模糊的，因為它們混合了邊界鄰域內屬于不同類別的點的特征.隨著網絡的深入，如果其他點包含邊界點的特征，那么邊界上的這些模糊特征將不可避免地分層傳播到更多點，導致不同物體的信息跨邊界傳播，不同物體之間的過渡區域被錯誤分割.為了解決這一問題，Gong 等人[59]首先提出了一個邊界預測模塊（boundary prediction module,BPM）預測邊界點；基于預測的邊界，設計了一個邊界感知幾何編碼模塊（boundary-aware geometric encoding module,GEM）對幾何信息進行編碼，使同一個鄰域內不同類別的局部特征不會相互影響；此外為了使得提取的特征更具區分性，還提出了一種輕量級幾何卷積運算（geometric convolution operation,GCO），通過幾何卷積核（geometric kernel）和鄰域內點的方向向量構成的矩陣相乘得到中心點的特征，在一個包含K個近鄰點的鄰域中，其幾何結構可用K個3D 方向向量表示.如圖7 所示，K=3 時，構造的幾何卷積核是一個具有3 個方向向量的矩陣，每個向量表示3D 空間中的1個方向，這3 個方向向量和中心點可以表示一個四面體（最簡單的多面體），因此卷積核本身可以描述點在方向上的分布.

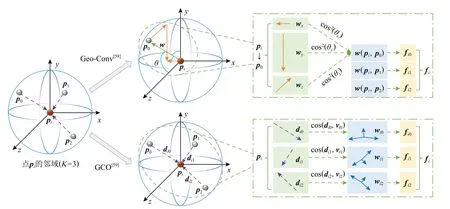
Fig.6 Geometric convolution operations圖6 幾何卷積運算

2）設計點的局部鄰域[60-61]

盡管采用球查詢和K近鄰的點鄰域搜索方式是直觀的、簡單的，但由于鄰域范圍R或近鄰點數K是預定義的，這也就限制了中心點的局部鄰域大小，同時該值設置的不合理也會導致網絡的性能變差.相比于圖7（a）中通過球查詢得到的球形區域（ball），Zhang 等人[60]提出了一種殼卷積算子（ShellConv），將中心點的3D 球形鄰域劃分為多個殼形區域（shells），即同心球殼（concentric spherical shell），一 個shell 表示2 個相同球心不同半徑的球面之間的空間范圍，如圖7（b）所示，同時構建包含多個ShellConvs 的殼卷積神經網絡（ShellNet），將中心點的K個近鄰點按照到中心點的距離升序排列并劃分到不同的殼內；同一個殼內的點，通過全連接層和最大池化層計算出一個局部特征，最后根據多個殼的局部特征加權求和得到中心點的聚合特征，提高了局部特征的學習效率.Lei 等人[61]定義了一個球卷積（spherical convolution）算子，利用空間分區將中心點的球形鄰域劃分為多個大小不一的箱形區域（bins），如圖7（c）所示，并為每個bin 定義一個可學習權重矩陣，該矩陣對位于該子區域內的近鄰點進行加權求和得到卷積結果.與標準卷積核相比，后者必須保持所有區域大小統一，并依靠提升分辨率來提取更細粒度的特征，這通常會導致較高的內存占用問題，而球卷積算子的多尺度區域解決了這一問題，使得卷積運算更加靈活，不僅能夠對相同區域特征實現權重共享，也有效學習了具有非對稱性的幾何特征.基于球卷積算子，還提出了八叉樹（octree）[62]引導卷積神經網絡（octree guided CNN,Ψ-CNN），該網絡具有與八叉樹深度相同數量的卷積層，根據八叉樹的數據結構對輸入點云進行空間劃分，分層下采樣得到中心點并構造點鄰域.隨后，由于球卷積算子的靈活性和優越性，Lei 等人[43]又將其擴展到圖卷積網絡中提出了SPH3D-GCN，此外，考慮到劃分邊界和密度分布的影響，將模糊機制（fuzzy mechanism）引入到該卷積算子中，提出了模糊核（fuzzy kernel），并在此基礎上構建了一個高效的適用于點云分割任務的圖卷積網絡SegGCN[42].

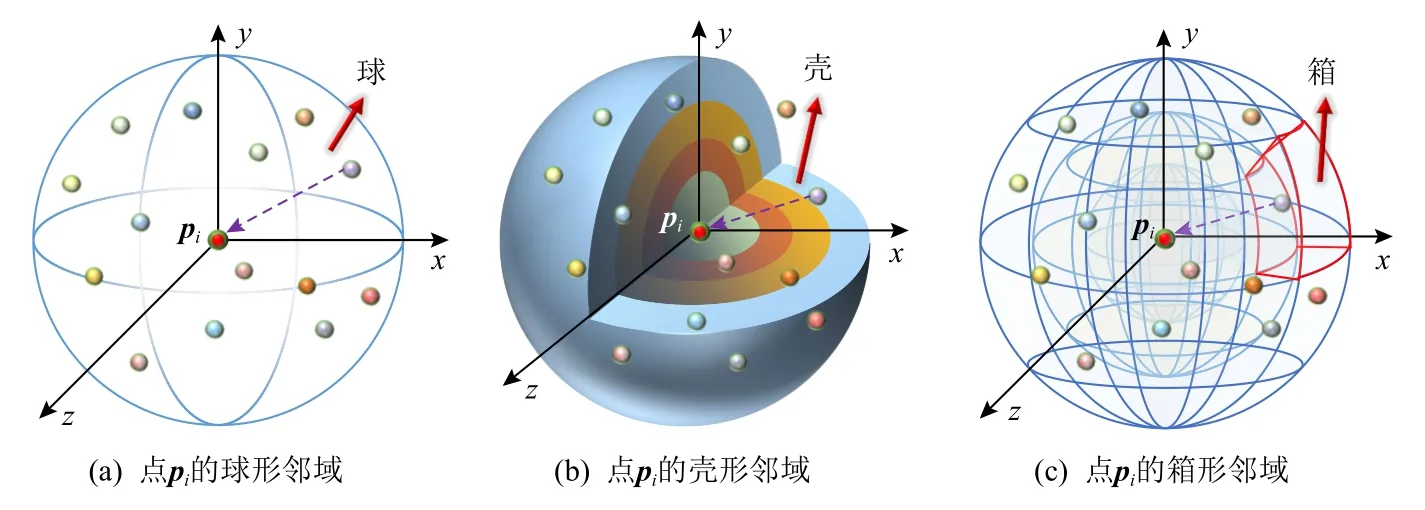
Fig.7 Point neighborhoods with different definitions圖7 定義不同的點鄰域

3）改變點卷積的感受野[63-66]

與2D 圖像卷積運算類似，在3D 點云中，決定卷積神經網絡某層的輸出結果中1 個特征所對應的輸入層的區域被稱作感受野，其大小直接關系到網絡處理各種任務的性能.因此，增加感受野大小的常用方法有2 種：一種方法是堆疊多個（點）卷積層，在提升網絡性能的同時也引入了更多的參數，增加了計算復雜度，導致額外的內存消耗；另一種方法是增大卷積核的尺寸，參考如圖8（a）和圖8（b）所示的1D和2D 空洞卷積原理，在擴大感受野的同時可以不損失信息，得到了如圖8（c）所示的3D 空洞卷積算子[63-64].Pan 等人[63]提出的點空洞卷積算子（point atrous convolution,PAC），通過設置不同的采樣率r在特征空間或度量空間中對中心點的近鄰點特征進行稀疏采樣（sparse sampling）.特別地，如果采樣率為r=1，則PAC 將退化為EdgeConv[39].這樣，在不增加參數量和計算量的前提下，通過增大采樣率就可以有效地擴大卷積的感受野.同樣，類似于2D 空洞空間金字塔池化（atrous spatial pyramid pooling,ASPP）[10]的原理，將不同空洞率的空洞卷積平行或者級聯堆疊來獲取多尺度信息，由此提出了點空洞空間金字塔池化（PASPP），得到不同采樣率下的近鄰點特征來聚合中心點的多尺度局部特征.最后，集成多個PACs 和PASPPs，構建了相應的具有排列不變性的點空洞卷積網絡（PointAtrousNet,PAN），充分利用局部幾何細節進行點云分析.類似地，Engelmann 等人[64]首先對比了不同尺度感受野對網絡性能的影響，然后提出了一種空洞點卷積（dilated point convolution,DPC）算子集成鄰近點的特征，通過設置不同的空洞因子d改進原先的K近鄰，擴大中心點的局部鄰域范圍，搜索K×d個近鄰點并僅保留排序后的每K個近鄰點集中的第d個點來學習核權重.特別地，如果r=1，則DPC 將退化為使用K近鄰尋找近鄰點的Pointwise Convolution[55].原先通過簡單地增加近鄰點數來提高網絡性能的方法會增加計算成本，從而導致推理時間變慢，而引入d后增加了點卷積的感受野大小，在幾乎不增加額外計算成本的情況下顯著提高性能.

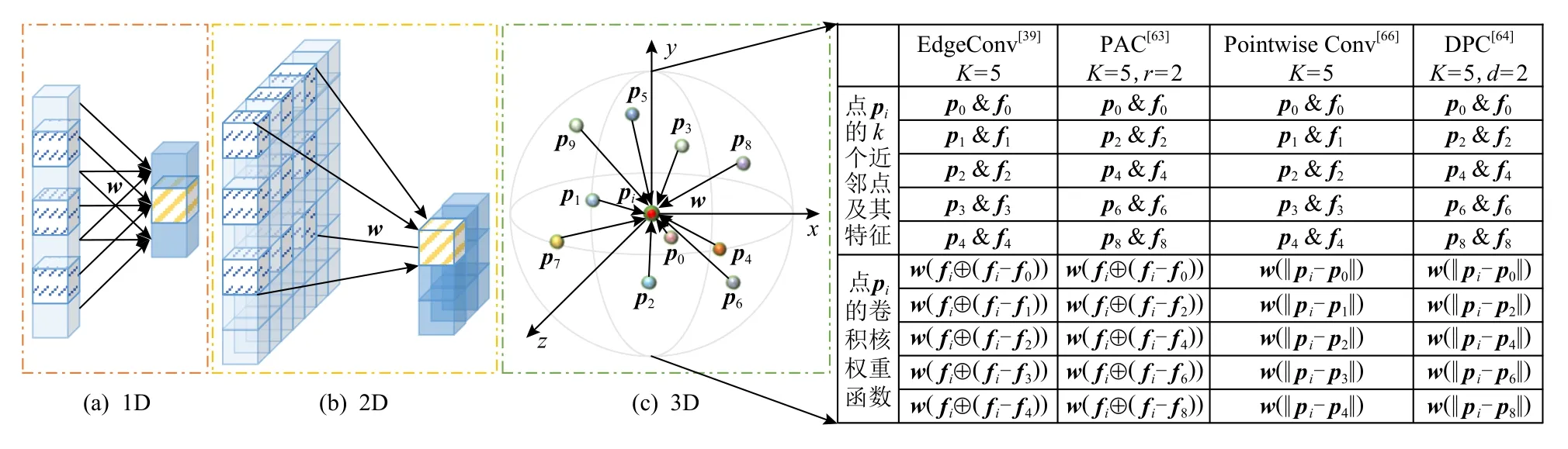
Fig.8 Comparison of dilated/atrous convolutions圖8 空洞卷積的對比

鑒于以往的研究工作大多只關注空間維度上的特征提取，而忽略了通道維度，使得點云的特征學習不充分，因此類比于2D 可分離卷積，Cui 等人[65]提出了一種輕量級注意力模塊（lightweight attention module,LAM），它采用了深度可分離卷積（depthwise separable convolution,DSConv）算子在不降低網絡性能的前提下提高計算效率，同時采用基于通道統計特征的注意力機制（attention mechanism）通過自動縮放不同特征通道的權重來提高網絡精度.DSConv 將作用在點云上的卷積運算分為2 個步驟，減少特征提取在空間和通道2 個不同維度上的相互干擾：①深度卷積（depthwise convolution）.在輸入的每個特征通道上單獨執行空間卷積；②點卷積（pointwise convolution[55]）.使用1×1 卷積將特征通道映射到新的通道空間，選擇不同的卷積核進行這2 個維度的卷積.為了解決3D 旋轉，即SO（3）、3D 變換，即SE（3）①SO(3)：特殊正交群(special orthogonal group)，指3D 旋轉(rotation)、旋轉矩陣到旋轉向量；SE(3)：特殊歐氏群(special Euclidean group)，指3D 變換=旋轉(rotation)+平移(translation)，也稱歐氏變換(Euclidean transformation).的等變性和不變性，Chen 等人[66]提出了一種用于點云的SE（3）可分離卷積（separable convolution,SPConv）算子，首先，將卷積分解為1 個SE（3）點卷積算子和1 個SE（3）組卷積算子，分別在3D 歐氏空間和SO（3）空間中交替進行卷積運算，使用SE（3）空間中定義的特征作為輸入并輸出每個點的SE（3）等變特征.SE（3）可分離卷積在不影響性能情況下顯著降低了SE（3）卷積的計算成本.其次，將注意力機制與全局池化相結合提出了一個組注意力池化（group attentive pooling,GAP）操作，進行從等變特征到不變特征的轉換②旋轉不變映射可以由具有等變對齊的任何映射構造.旋轉等變映射可以由具有等變對齊的任何旋轉不變映射構造.與不變性相比，等變性保留而不是丟棄空間結構，是更具區別性的表示..最后，集成卷積和池化構建了一個SE（3）等變點網絡（equivariant point network,EPN）作為通用框架，可以根據下游任務生成等變或不變的點特征.

4）構建點與卷積權重的相關性[67-69]

考慮到注意力機制在提取全局特征上的優越性，為了幫助卷積得到更細粒度的特征，Dang 等人[67]提出了鄰域注意力卷積（neighborhood attention convolution,NAC），在不同的近鄰點上自適應地進行特征選擇，充分挖掘每個局部區域內的細粒度局部幾何特征，通過融合中心點與近鄰點的相對位置、絕對位置和高維非局部點特征來獲得鄰域注意力系數.使用Softmax 函數將所有近鄰點的鄰域注意力系數歸一化到范圍（0,1）來表示不同近鄰點的重要性.然后，基于NAC 并結合2D 組卷積的原理，又提出了分層交錯組卷積（hierarchical interleaved group convolution,HIGConv），包含第1 階段分層組卷積（PHGC）和第2階段分層組卷積（SHGC）.具體來說，PHGC 將NAC的輸入特征和參數劃分為多個分區，為了便于不同分區之間不同級別的特征映射的交互，將相鄰2 個分區的特征在通道維度上進行融合作為下一個分區的輸入特征，以擴大輸出特征維度、增強學習能力.最后，連接所有分區的輸出特征并在特征通道維度上進行洗牌（shuffle），以充分融合所有分區的特征，提取細粒度的局部幾何特征.類似地，SHGC 通過將多層感知機的輸入特征和參數劃分為多個分區并在通道維度上進行洗牌后提取得到可區分的非局部點特征，這樣豐富的局部到全局形狀信息可以通過2部分的輸出特征聚合在一起.然后，構建包含多個HIGConvs 的分層交錯組卷積神經網絡（HIGCNN），其核心是多尺度關系（multi-scale relation,MSR）模塊，用于集成不同尺度區域之間的關系，對多尺度細粒度特征進行編碼，將2 個區域的局部幾何特征融合為關系描述符，通過Softmax 函數將其歸一化到范圍（0,1）內生成區域之間的關系分數，用于自適應地增強有用的結構特征，抑制無用的噪聲特征，從而以較少的冗余參數和較低的計算成本獲得足夠的特征表示能力.

此外，Mao 等人[68]提出了一種插值卷積（interpolated convolution,InterpConv）算子來度量輸入點云與卷積權重之間的幾何關系.在每個權重向量附近找到一組輸入點，然后對它們的特征進行插值以分配給權重矩陣進行卷積運算.由此提出了2 種插值函數：三線性插值（trilinear interpolation）和高斯插值（gaussian interpolation）.它們的權重計算方法不同，三線性插值通過計算相對于中心點的8 個晶格點的權重坐標，然后使用這些權重將輸入點特征反向分配給相鄰的權重坐標，再進行加權求和得到中心點的新特征.而高斯插值是使用高斯函數來計算權重.其他函數，如線性基函數（linear basis functions），也可以用作插值函數.級聯多層多感受野的InterpConvs 以構建插值卷積神經網絡（interpolated CNN,InterpCNN），解決點云的排列不變性，且對點云密度不敏感，但其存在的一個缺點是預先指定的插值函數無法適應點云的變化，導致其魯棒性較差.在特征提取過程中，需要進行逐步下采樣來減少點的數量，增加特征維度.為了在這一過程中不丟失點云的幾何形狀信息，Nguyen等人[69]提出了一種統計卷積（statistical convolution,StatsConv）算子，利用統計學中的樣本矩，結合基于從點云中提取的不同矩的全局特征和輸入點進行非線性變換后的逐點特征，通過幾個非線性全連接層投影到一個新的特征空間；封裝了全局特征和局部特征，用于提取各種統計信息來表征輸入點集的分布信息.

2.2 連續卷積

連續卷積方法是在連續的空間中定義卷積算子，其中近鄰點的權重與中心點的空間分布有關.連續卷積運算最重要的部分是特征建模的方式.考慮到實際任務的復雜性，卷積核函數也可能是極其復雜的，因此主要有2 種策略：一種策略是增加一些虛擬化的輔助信息；另一種策略是對所使用的卷積核函數進行參數化.

2.2.1 虛擬化輔助信息

為了保留3D 點坐標編碼的全局信息，一些研究工作通過增加或者設計一些虛擬點[70-72]、虛擬空間[73-74]、虛擬結構[75-76]來輔助進行卷積運算，如圖9所示.

1）虛擬點

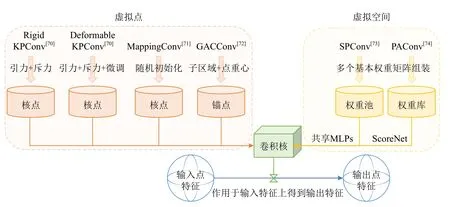
Fig.9 Introduction of virtualization auxiliary information圖9 引入虛擬化輔助信息

首先，Thomas 等人[70]引入了核點（kernel points）并提出了一種核點卷積（kernel point convolution,KPConv）算子，在中心點的球形鄰域內確定一組任意數量的核點集合，每個核點帶有一個可學習的權重矩陣，相關系數取決于任意點與核點的相對位置（歐氏距離）.通過分別計算鄰域內的所有近鄰點與核點的權重矩陣的乘積對該點進行特征變換，最后累加所有近鄰點的特征得到中心點的特征.由此可見，核點位置對卷積算子至關重要，因此通過解決一個球形空間中最佳覆蓋的優化問題來計算核點位置，并進一步提出了處理簡單任務的剛性卷積（rigid KPConv）算子和處理復雜任務的可變形卷積（deformable KPConv）算子.對于剛性卷積，球心（中心點）作為一個核點；球心對其他核點有一定的引力（attractive force）來吸引它們靠攏；其他核點之間有一定的斥力（repulsive force）來使它們相互遠離.這個由引力、斥力組成的系統穩定后，即可確定每個核點位置.對于可變性卷積，按引力、斥力的方法確定出來的所有核點的位置可能不是最優的，因此通過計算核點相對于原始位置的偏移量來優化或微調每個核點的位置.在此基礎上，還構建了含有多個KPConvs的分類網絡（KP-CNN）和分割網絡（KP-FCNN），每個卷積層采用下采樣以在不同密度的點云下實現高魯棒性.同樣，Yan 等人[71]也引入了核點并提出了一種映射卷積（mapping convolution,MappingConv）算子，不同的是MappingConv 中的核點位置最初是在以中心點為球心的單位球形鄰域中隨機初始化生成的，根據3 個多層感知機學習到的映射函數，基于近鄰點和核點之間的空間位置關系（歐氏距離）將不規則的近鄰點特征映射到一系列可學習的核點上，然后通過反向傳播以數據驅動的方式對核點位置進行更新.最后將學習到的權重應用于位于核點上的聚合特征集合得到卷積結果.類似地，Zhang 等人[72]引入了錨點（anchor points）并提出了一種全局上下文感知卷積（global context aware convolution,GCAConv）算子.為每個中心點生成一組錨點集合來近似表征全局輸入形狀特征.這里的錨點位置對卷積算子同樣至關重要，因此以中心點為原點構造一個全局加權局部參考系（global weighted local reference frames,LRF），通過投影將近鄰點的3D 全局坐標轉換為局部坐標，根據LRF 將該中心點的局部鄰域劃分出8 個細分鄰域子空間，將每個鄰域子空間中近鄰點的重心作為錨點，通過1D 卷積編碼局部點集和全局錨點之間的局部和全局關系（local-global relation）來定義卷積權重，執行卷積以提取局部和全局特征（local-global feature）.

2）虛擬空間

首先，Yang 等人[73]定義了一個可學習的卷積權重池（weight pool），并提出了一種空間探測卷積（space probing convolution,SPConv）算子.首先采用一個幾何引導的索引映射函數（index-mapping function），將中心點與近鄰點之間的幾何特征轉換為權重索引，學習自適應地將3D 空間劃分為多個子空間以進行局部幾何結構識別.然后從權重池中為每個子空間中的點分配一個共享的權重矩陣；將每個近鄰點的幾何特征輸入到共享多層感知機中，輸出的特征映射被視為每個子空間所屬的等級.最后與相應的權重進行卷積和聚合，以獲得更深層次的語義特征.類似地，Xu 等人[74]定義了一個可學習的卷積權重庫（weight bank），并提出了一種位置自適應卷積（position adaptive convolution,PAConv）算子和一個分數網絡（ScoreNet），將中心點及其近鄰點之間的相對位置關系向量輸入到網絡中以自適應學習對應的歸一化在（0,1）范圍內的系數向量，根據向量中的概率值組合權重矩陣，值越高表示位置向量和權重矩陣之間的關系越強.通過組合存儲在權重庫中的基本權重矩陣與網絡預測出的位置自適應系數來構造動態卷積核函數用于卷積運算.這2 項工作都是通過建模點之間的位置關系來提取幾何空間特征，但存在的問題是存儲過多的權重矩陣可能會造成網絡冗余，帶來較大的內存占用和計算負擔，因此選擇合適的權重矩陣是決定二者網絡性能的關鍵.

3）虛擬結構

為了加快計算速度，Groh 等人[75]提出了一個卷積算子Flex-Convolution，將卷積核的權重定義為中心點的局部鄰域上的標準標量積，并與其K個近鄰點的特征向量進行卷積運算，網絡還集成了采用類似方法的最大池化Flex-Max-Pooling 進行聚合操作，使用較少的參數和較低的內存消耗得到了極具競爭力的性能.隨后，Boulch[76]提出了一種卷積算子ConvPoint，將卷積核劃分為空間核權重和特征核權重，混合幾何空間和特征空間.幾何空間使用多層感知機來學習卷積核與點云之間的關系函數，即稠密加權函數，然后與特征空間加權融合得到卷積輸出.這2 個卷積算子在選擇近鄰點時均使用了二叉樹（kdtree）[77]代替K近鄰，并使用索引列表存儲近鄰點集，使得卷積對輸入點云密度具有魯棒性.

2.2.2 參數化核函數

首先，Wang 等人[78]提出了一種參數化連續卷積（parametric continuous convolution）算子，依據萬能近似定理（universal approximation theorem），采用多層感知機計算卷積核函數，因為它能夠逼近任何連續函數，這樣卷積的輸出可以是整個連續向量空間中的任意點.通過級聯多個該卷積算子的卷積層構建深度參數化連續卷積網絡（deep parametric continuous CNN,PCCN）.然而該方法只能近似深度方向的卷積，而不能近似實際卷積.Xu 等人[79]提出了卷積算子SpiderConv，將連續卷積核函數定義為階躍函數和定義在K近鄰上的泰勒展開多項式的乘積.階躍函數通過計算中心點及其近鄰點之間的測地線距離（geodesic distance）來獲取粗糙的幾何結構；泰勒展開式通過在中心點及其近鄰點構成的立方體頂點處進行插值來學習局部的細粒度幾何結構.同樣通過級聯多個帶有SpiderConvs 的卷積層構建卷積網絡SpiderCNN，與該卷積算子和網絡的思想最為接近的是處理體素輸入的稀疏卷積網絡SparseCNN[25].Hermosilla 等人[80]提出了一種蒙特卡洛卷積（Monte Carlo convolution）算子，Wu 等人[81]提出了一種稱為PointConv 的卷積算子，二者均將卷積運算視為蒙特卡洛估計（Monte Carlo estimate）的過程，由權重函數和密度函數組成的非線性函數.使用多層感知機近似卷積核權重函數，采用核密度估計（kernel density estimation）學習概率密度函數（probability density function,PDF），用來重新加權學習的權重函數，這就使得蒙特卡洛可以處理不同采樣密度的點云.然后分別構建了各自的蒙特卡洛卷積網絡進行分層點云特征學習.Wang 等人[82]提出了一種片元卷積（PatchConv）算子，首先遍歷全局空間，為每個中心點構建PointPatch 模塊，即以中心點為原點將3D 局部鄰域劃分為8 個卦限（octant），并搜索每個卦限中的近鄰點作為該卦限的特征；如果在一個卦限內沒有近鄰點，就選擇中心點特征作為該卦限的特征.卷積核權重函數被視為一個由多層感知機近似的利普希茨連續函數（Lipschitz continuous function），在每個掛限進行卷積運算提取中心點的高維特征.進一步構建了一個帶有PatchConvs 的輕量級卷積網絡PatchCNN 以有效集成每個PointPatch 模塊中的特征.Liu 等人[83]提出了一種基于鄰域集合關系推斷的卷積（relation-shape convolution,RS-Conv）算子作為卷積網絡RS-CNN 的核心，計算每個局部鄰域中的近鄰點與中心點之間的關系，包括低維關系（lowlevel），即兩點坐標之間的歐氏距離和兩點特征之間的相對距離；高維關系（high-level），即更抽象的點關系表示.使用多個共享多層感知機近似卷積核來學習局部鄰域中點之間關系的映射.隨后，Liu 等人[84]又提出了一種卷積算子PConv，將卷積運算分解為2個核心步驟：1）特征變換（feature transformation）.卷積核函數被定義為帶有非線性激活器的共享單層感知機（single-layer perceptron,SLP）以提高其效率.2）特征聚合（feature aggregation）.使用聚合函數來聚合這些變換后的特征.然后基于PConv 構建了DensePoint模塊，所有前面層的輸出都用作其輸入，其自身的輸出用作所有后續層的輸入，這樣每層都可以獲得特定級別的信息.最終，聚合得到豐富的局部語義信息和全局形狀信息.由于點云的稀疏性，Atzmon 等人[85]提出了一種稀疏卷積（sparse extrinsic convolution）算子并構建了相應的點卷積神經網絡（PCNN）來處理點云任務，應用徑向基函數（radial basis function,RBF）進行卷積，這一參數化過程沒有任何的離散化操作或者近似操作.隨后，Poulenard 等人[86]基于PCNN[85]提出了球諧卷積神經網絡（SPHNet），使用球諧（spherical harmonics）函數定義了一種非線性旋轉不變卷積（spherical harmonics convolution,SPHConv）算子來實現旋轉不變性.對比二者的網絡結構與性能如表1 所示.

SPHNet[86]是首次強調旋轉不變性對于點云分析任務重要性的研究工作，這就要求當給定任意的旋轉角度或方向時，輸出相同的分析結果，如之前提到的SO（3）和SE（3）[66]，使網絡對點云的旋轉具有魯棒性.一種常見的解決方案是使用任意旋轉來增加訓練數據，但這樣做的局限性是存在一些不可預見的旋轉，而且由于訓練數據量的增加，訓練時間復雜度也會隨之增大.因此為了解決這一問題，一些研究人員陸續展開了相關研究并提出了一些具有旋轉不變性的點云卷積算子.Zhang 等人[87]基于兩點之間的歐氏距離和角度特征，提出了一種旋轉不變卷積（rotation invariant convolution,RIConv）算子.由于這些幾何特征在剛性變換下是不變的，而且不像點坐標是唯一的，許多點共享相同的距離和角度，因此它們非常適合于構造具有旋轉和平移不變性的卷積算子.然后使用共享多層感知機將這些幾何特征從3D 空間提升到高維空間，并進行卷積運算提取特征.這2種方法的優點是允許在訓練/測試場景中旋轉或不旋轉的情況下進行一致的預測，并且魯棒性強，可以推廣到具有不可見旋轉的輸入數據中.盡管如此，這2種方法的性能有時可能不如一些具有平移不變性的點云卷積算子[56,60]，詳見第3 節.此外，由于RIConv[87]將3D 坐標轉換為一些旋轉不變的特征，例如距離和角度，導致3D 坐標編碼的全局信息丟失.為了解決這一問題，GCAConv[72]利用了局部參考系（LRF），其原理是，卷積與任何映射函數一樣，可以通過對齊輸入與旋轉等變映射（rotation-equivariant mapping）的結果，將其轉換為旋轉不變映射（rotation-invariant mapping），這樣就將輸入點云的全局特征信息集成到了卷積運算中.參考這一方法，同時由于KPConv[70]性能優異、定義直觀、靈活性強，且能夠直接將特征與空間定義的卷積核相結合，Thomas[88]結合旋轉等變性和旋轉不變性之間的內在聯系[66]設計了一種旋轉不變性的多對齊卷積（multi-alignment KPConv,MAKPConv）算子.為了能夠提取更準確的信息，首先設計了一個對齊模塊（alignment module），假設每個輸入點都有一個旋轉等變LRF，這些LRFs 可以重新排列成旋轉不變的LRFs，并用共享多層感知機對該信息進行編碼轉換為旋轉不變特征，輸出與輸入特征尺寸相同的特征，可以視為近鄰點的LRF 和中心點的LRF 之間的變化關系，該特征提供了有關鄰域的幾何信息.將輸入特征與對齊特征進行連接作為標準KPConv[70]的輸入進行卷積操作輸出最終特征.這種變換的原理是只要LRF 是旋轉等變的，對應的特征是旋轉不變的，這個對齊卷積的輸出就是旋轉不變的.然后，設計了一個多對齊模塊（multi-alignment module），假設每個輸入點都有多個旋轉等變LRFs，通過在每個LRF 上使用對齊卷積運算以獲得一組對齊輸入，采用核相關性為每個對齊輸入聚合核點上的特征，連接起來使用卷積核，有效地聚合來自不同對齊的信息，而不同于KPConv[70]為每個對齊輸入使用單獨的卷積核.但由于使用了不變性特征而減少了卷積必須學習的形狀多樣性，這可能會降低網絡的學習能力和魯棒性.

Table 1 Comparison of Network Structures and Performance on PCNN and SPHNet表1 PCNN 與SPHNet 的網絡結構與性能對比

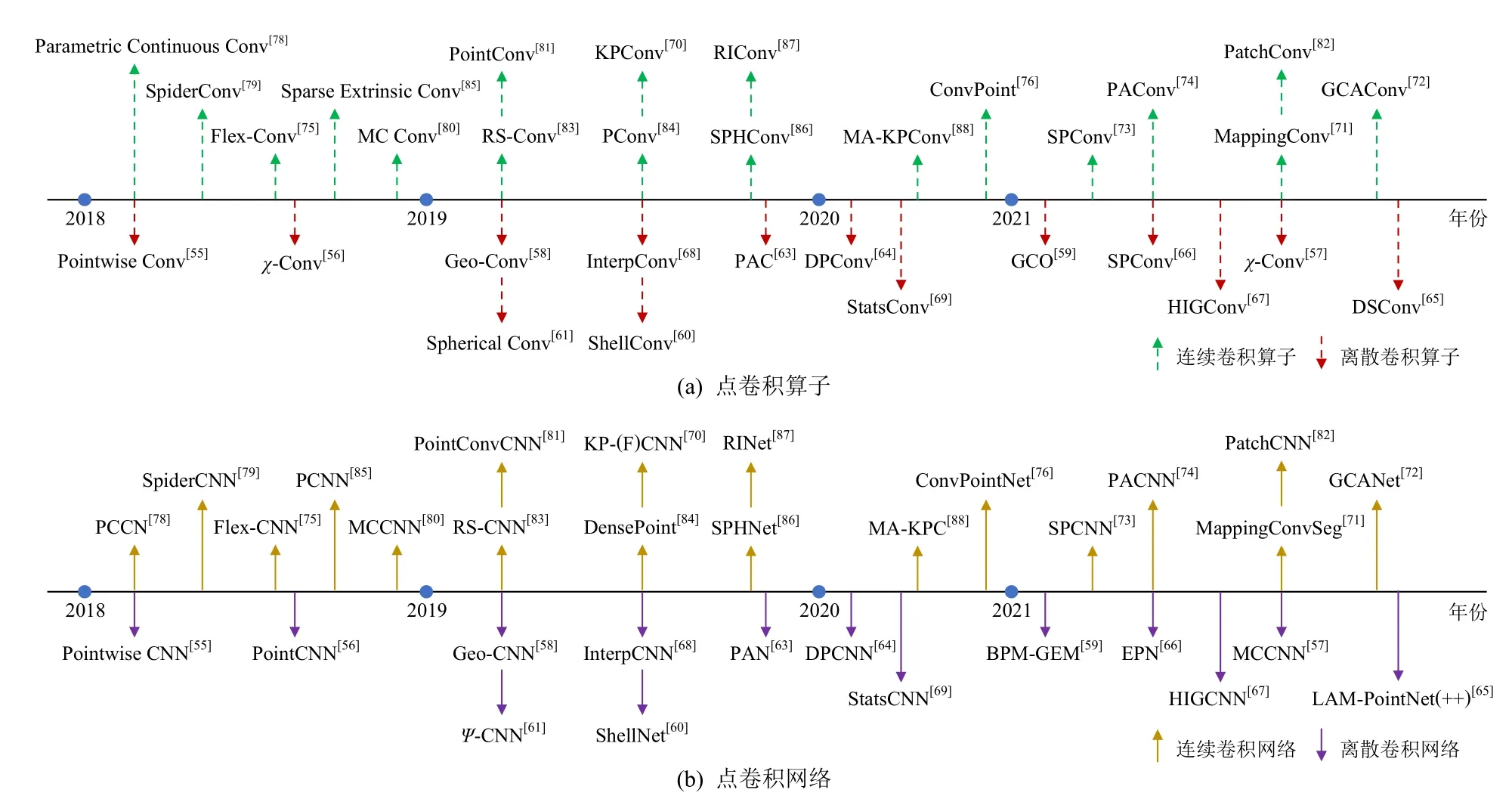
Fig.10 Chronological overview of point-based convolution methods圖10 基于點的卷積方法概覽

綜上所述，類似于文獻[3]中對點云任務的各個深度學習方法進行的較為直觀的列舉方法，本文按照時間順序將現有的基于點的卷積算子（如圖10（a）所示）及其對應的網絡結構（如圖10（b）所示）進行了整理與匯總.同時，本文為這些基于點的卷積算子搭建了一套獨特的分類體系，如圖11 所示.此外，我們還將其所對應的卷積網絡進行了分類整理，如表2所示，并對各個方法的優缺點進行了總結.與離散卷積方法相比，連續卷積方法更適合捕捉3D 點云的局部幾何特征.綜合分析對比連續卷積的2 個策略，可以得出，有時候使用參數化表示會使卷積算子更加復雜，待訓練參數較多，學習效率低下，網絡的收斂性也更加困難，還容易出現過擬合，適應性較差.而使用幾何特征可以保留物體最初的形狀信息，但一些引入虛擬點或空間會消耗內存，其位置選取對網絡的最終性能有著至關重要的影響，根據一些先驗信息或規則預定義虛擬信息也一定程度上限制了網絡的靈活性，導致性能會有所降低，可能需要針對不同的數據集或主干架構進行專門優化.

卷積網絡應用在點云處理任務上的性能會在第3 節中重點進行分析對比.

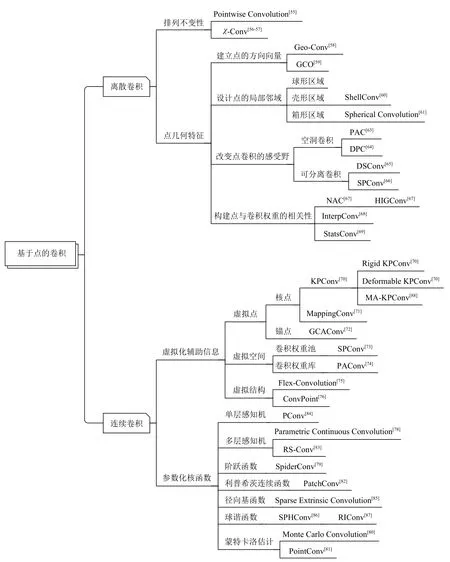
Fig.11 Classification of point-based convolution operators圖11 基于點的卷積算子分類

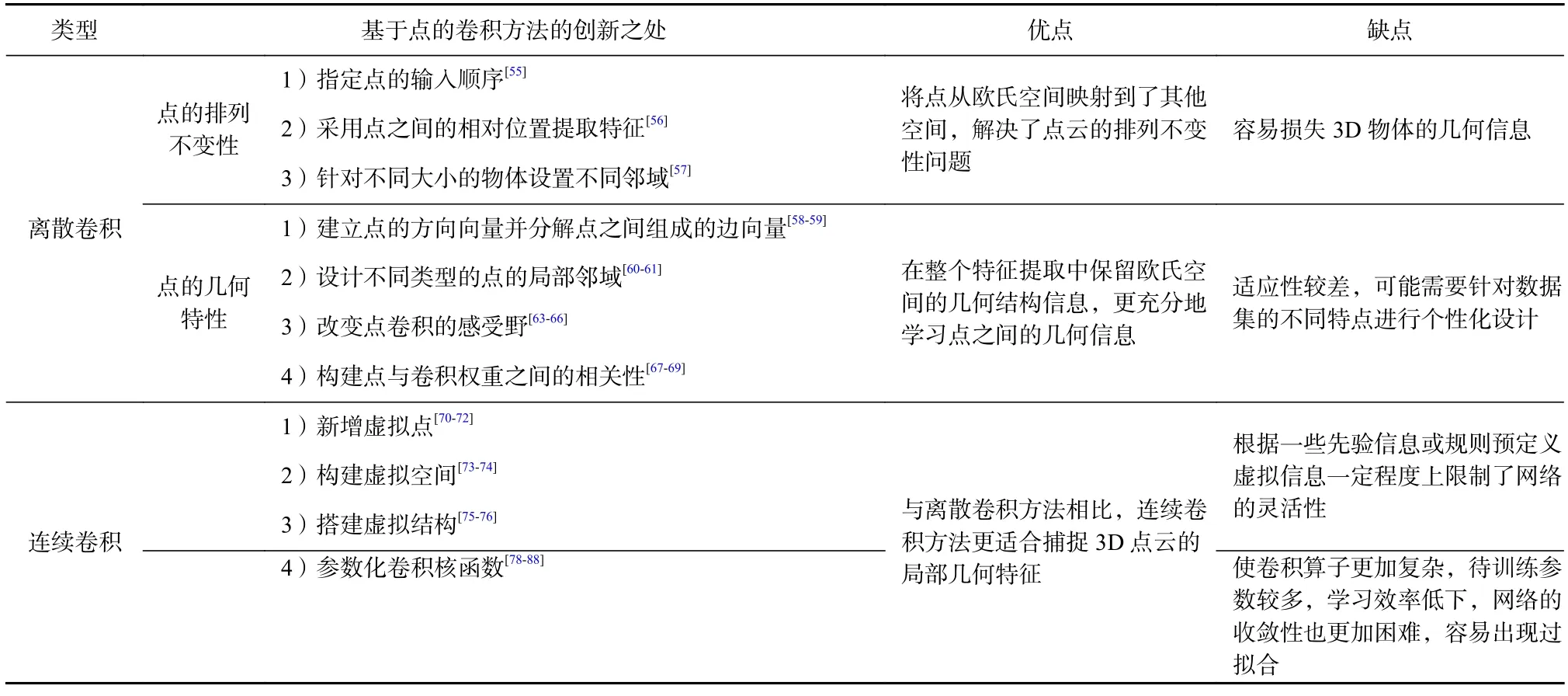
Table 2 Classification and Comparison of Point-Based Convolution Methods表2 基于點的卷積方法分類與對比

本文根據卷積運算的類型（即離散卷積和連續卷積）對各個點卷積算子及其對應的網絡結構進行了分類與整理.同時，本文將圍繞這些卷積方法進一步分析卷積算子的原理，對比分析基于點云的卷積網絡在分類與分割等具體任務中的性能，最后進行總結及對未來相關研究的展望.

本文跟蹤了點云領域最新的研究進展，并在前人工作的基礎上進行了補充完善和深入挖掘.首先，在算法內容上，本文將重點聚焦在基于3D 點云的卷積運算方法上，并且添加了最近提出的基于點云的卷積新方法，總結了30 多種應用于點云上的卷積運算和卷積網絡，并對其進行了更深入地調研和更詳細地展開，同時深入挖掘了各個卷積運算和卷積網絡之間的區別與聯系.根據3D 點云數據處理方式，將它們分為2 類：離散卷積和連續卷積.關于離散卷積，細分為針對點的排列不變性進行的卷積運算和針對點的幾何特性進行的卷積運算；關于連續卷積，細分為添加虛擬化輔助信息后進行卷積運算和參數化核函數后進行卷積運算.與以上綜述[47-53]相比，本文從學習方法的角度而非點云任務的角度來探討現有文獻如何對在點云上的卷積運算和卷積網絡進行設計，從而進行更充分的特征提取，使得其更好地服務于下游的特定任務，包括點云分類和分割.其次，在應用內容上，本文歸納了基于點的卷積神經網絡的基本框架，并在此基礎上整理了現有研究中分類和分割網絡的具體網絡結構，此外還增加了對常見的真實場景數據集的介紹與對比工作.最后，在未來研究方向上，本文在基于3D 點云的卷積運算技術評述的基礎上，對點云領域未來研究方向進行了展望并給出各類技術的參考性價值.

3 點云任務應用

針對第2 節提出的關鍵要求3），本文綜述的各類研究工作的思路一般包括3 步：首先將其提出的點云卷積算子集成到分類或分割網絡框架中；然后將各個集成后的網絡應用到點云分類、分割等任務中進行實驗分析；最后根據實驗結果通過對比集成后的網絡與原始網絡的性能來進一步驗證所提出的點云卷積算子的有效性和優越性.鑒于點云分類、分割任務是3D 目標檢測與跟蹤、3D 場景重建與理解等更復雜且重要的下游任務的基礎，在本節中，我們選取4 個常見點云任務來進一步分析研究，如表3 所示，通過對比各個點云任務的結果來分析由不同點云卷積算子集成后的網絡的性能，從原理上挖掘卷積方法取得相對較優結果的原因，深入探索各個卷積運算的優劣，從而給出一些對未來更深入研究的建議與啟發.

3.1 網絡框架

大多數研究工作中涉及到的分類與分割網絡的基礎框架與2D 圖像的卷積神經網絡框架相似，如圖12 所示，其中，類似于LeNet-5[6]的分類網絡，首先經過包含1 個或多個串聯的卷積層的編碼器對點云進行特征提取和變換，采用不同的卷積算子以逐層提取輸入點的特征，點的數量逐漸減少，點特征的維度逐漸增多；然后再經過包含1 個或多個全連接層的分類器（classifier）對點云進行歸類，最終得到分類結果.類似于U-Net[9]的分割網絡，是一個具有跨層連接（skip connections）的編碼器-解碼器（encoderdecoder）體系結構.分割網絡與分類網絡共享同一個編碼器，主要用于特征提取（feature extraction），經過編碼器中的卷積層提取到的特征稱作局部特征，包括了每個點特征和點之間的關系特征.解碼器主要用于特征傳播（feature propagation），由于分割任務是逐點的標簽預測，所以需要將特征輸入到解碼器中，經過反卷積層或者其他操作（如插值、池化）進行特征擴展使得點云達到原始分辨率，點的數量逐漸增多，點特征的維度逐漸減少，得到的特征稱作全局特征.最終將局部特征和全局特征逐層連接起來，就可以得到用于分割任務的全部信息，同一個集合的點具有相似或相同的屬性和標簽，因此要歸為同類（即物體上的某一個部件或場景中的某一類物體）.需要注意的是圖12 的網絡框架圖只包含了網絡的最主要部分，即卷積層（convolutional layer）（該層是各個網絡的核心，與所使用的卷積算子有關，內部結構均不相同）、反卷積層（deconvolutional layer）、全連接層（full connection layer），其余的如池化層（pooling layer）、上采樣層（upsampling layer）、插值層（interpolation layer）、批歸一化層（batch normalization layer）、激活函數層（activation layer）等，在具體網絡具體涉及到的層數和連接順序均有所不同，具體網絡結構如表4 所示.

Table 3 Point Cloud Tasks and Their Basic Frameworks表3 點云任務及其基礎網絡框架

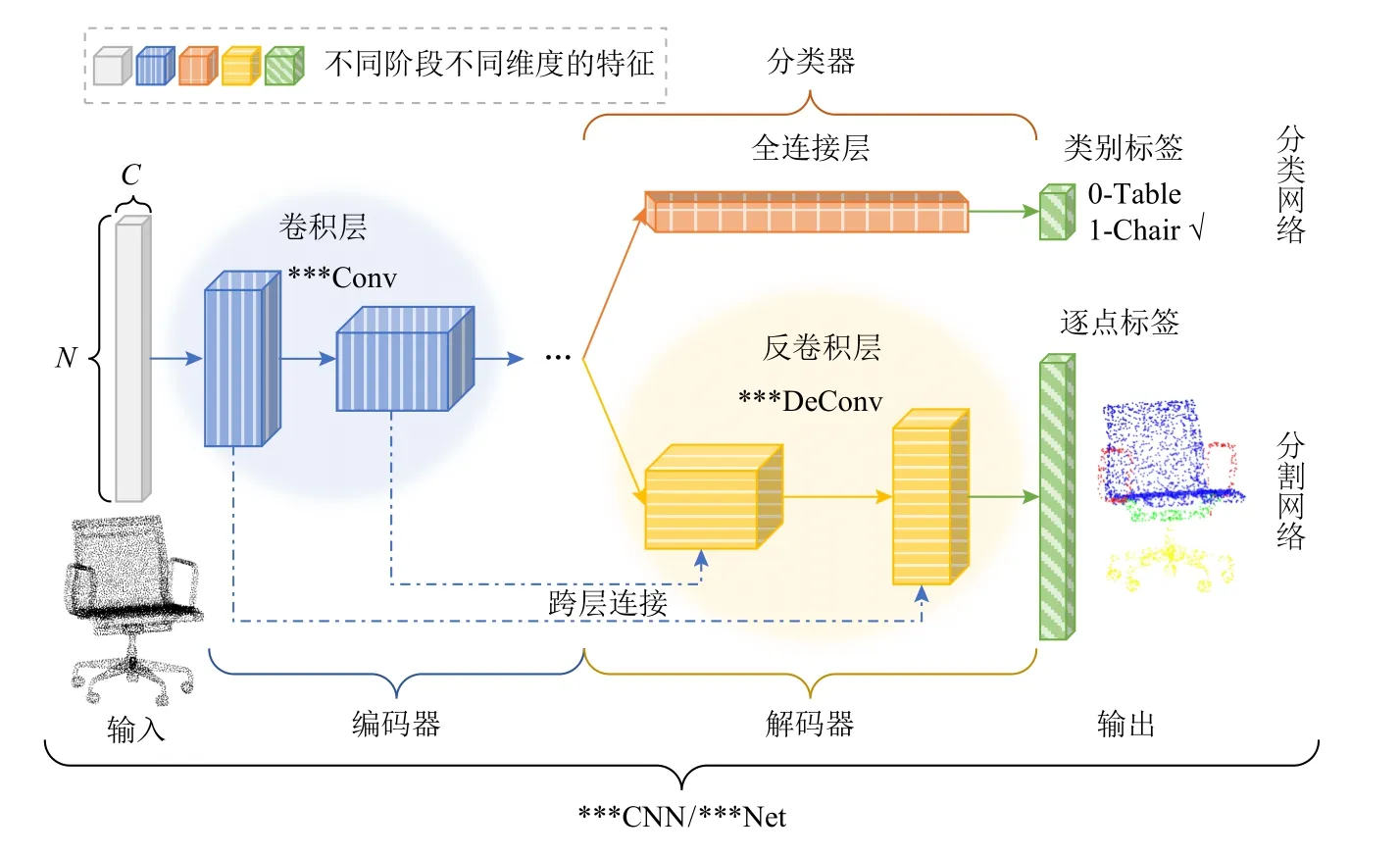
Fig.12 Basic frameworks of point-based CNNs圖12 基于點的CNNs 的基本框架

第2 節中總結的基于點云的卷積算子大多是即插即用的，在不改變其他原始的網絡配置（如網絡層數、特征通道數）的情況下，將某個卷積算子（***Conv）嵌入到經典的點云任務網絡中，以評估該算子的有效性并最大程度地減少復雜網絡架構的影響.關于這些網絡，它們統一的訓練流程大致如圖13所示，其中，最重要的部分就是集成了特定卷積算子的卷積層作為特征提取模塊，特征提取不充分將嚴重影響點云分類和分割任務的精度.

接下來，本文重點對比分析了形狀分類、部件分割、語義分割、法線估計這4 個具體任務中各個網絡的性能.需要注意的是，由于部分論文代碼未開源，無法在同一個實驗設備、相同網絡參數的情況下一一復現本文綜述的所有卷積方法，我們借鑒了近些年來的大多數綜述論文（如文獻[3]）的結果處理方式，提取各個論文中給出的對比結果并進行了歸納總結.因此，這里的實驗結果僅考慮了在相同評價指標和相同數據集的前提下進行對比分析.由于各個研究工作所使用的軟硬件條件和實驗環境可能各不相同，卷積算子所集成的基礎網絡框架也各不相同，最終的性能對比結果的準確性也會有所影響，最終得到的結果也屬于相對較優值而非絕對最優，其他具體情況還需進一步具體分析.

Table 4 The Specific Network Structures of Classification and Segmentation Networks in Existing Research表4 現有研究中分類和分割網絡的具體網絡結構

3.2 形狀分類

參考關于深度學習在點云上的研究綜述[3]，本文整理了相關的用于3D 點云形狀分類任務的數據集和評估指標，并在此基礎上，對各個卷積網絡的性能進行了對比分析.

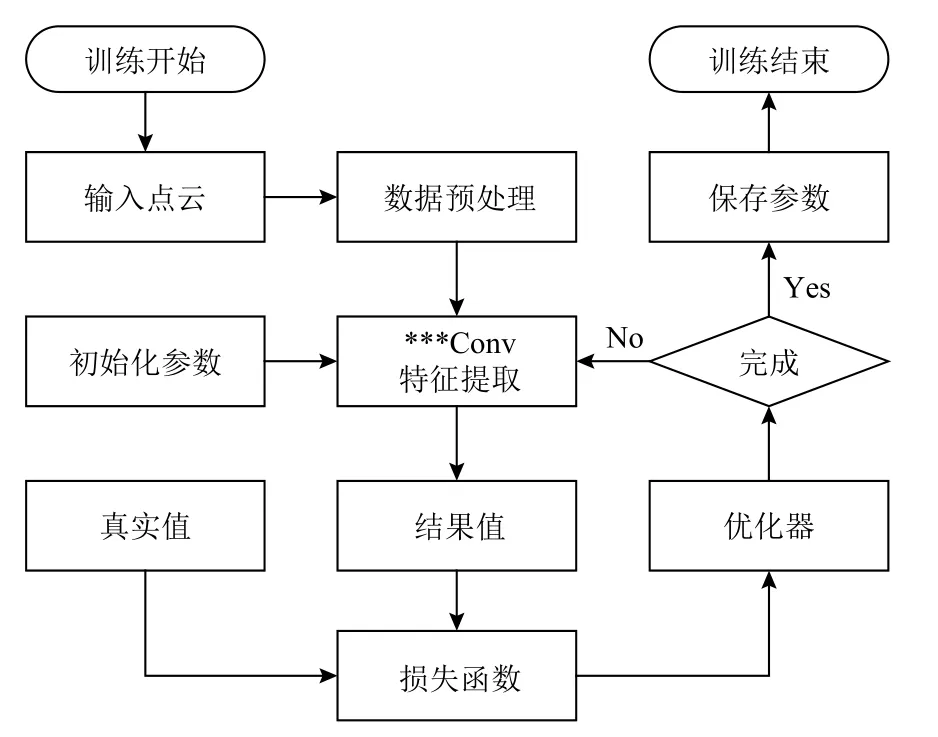
Fig.13 The training flow of point-based CNNs圖13 基于點的CNNs 訓練流程

1）數據集.為了測試不同的卷積運算在3D 點云形狀分類任務中的結果，現有研究工作使用的公開數據集主要是合成數據集（synthetic datasets）——ModelNet10/40（2015）[89].ModelNet 數據集包含了來自662 個類的127 915 個3D目標物體，其子集ModelNet10 包含了來自10 個類的4 899 個目標物體，ModelNet40 包含了來自40 個類的12 311 個目標物體.數據集中的目標物體是完整的，沒有任何遮擋和背景噪聲的影響.注意：由于在ModelNet10 數據集上進行分類實驗的研究工作數量較少，這里忽略不計，僅對比在ModelNet40 數據集上的結果.

2）評價指標.為了評估這些卷積運算在3D 點云形狀分類任務中的性能，現有論文提出了不同的分類網絡性能評價指標，常用指標為：

①總精度（overall accuracy,OA）.被正確分類的類別數與總類別數之間的比值.該值雖然能很好地表征總體分類精度，但對類別個數較多且不平衡的數據集來說影響較大.

②平均類精度（mean class accuracy,mAcc）.每個形狀類別內的被正確分類的個數與總個數之間的比值.該值適用于類別個數較多且不平衡的數據集，可以表征各自類別的分類精度.

3）對比結果.表5 列舉了各個研究工作中的點云分類網絡在形狀分類任務上的性能并進行了結果對比，主要包括輸入類型（點坐標P/法向量N）和2 個評價指標在ModelNet40 數據集上的結果.為了更全面地對比各個卷積網絡的性能，表5 中除了列舉了基于點的卷積網絡外，還列舉了引言中提到的一些其他的有代表性的方法，包括先驅工作PointNet[4]和PointNet++[5]、基于投影的方法ACNN[14]和A-CNN[16]、基于體素的方法3DmFV-Net[23]、基于晶格的方法SFCNN[26]、基于圖的方法SPH3D-GCN[43].

4）結果分析.OA 值是針對整個數據集的全體數據來說的（不區分類別），而mAcc值則是先計算每一個類別的準確率，再取平均值.當每個類別的數據量相等時，則OA值等同于mAcc值；反之，OA值主要受數據量相對較大的類別的準確率影響，mAcc值則主要受數據量相對較小的類別的準確率影響.也可以認為OA值和mAcc值的差別在于對每種類別的準確率其權重不同，OA值是根據該類別數據量與總數據量比值率確定權重，而mAcc值是平均分配.通過分析這2 個評價指標的區別，我們可以得出，并不是OA值最優的網絡其mAcc值就一定也是最優的，二者的側重點是不同的，因此，本文通過單獨對比各個網絡的OA值和mAcc值并找到各自指標下相對較優值，對其進行原理上對某些方法取得較優結果的原因進行深入探索.

Table 5 Comparison Results of Classification Networks'Performances on the ModelNet40 Dataset表5 分類網絡性能在ModelNet40數據集上的對比結果%

對比各個網絡的OA值可以得出目前相對較優的網絡是PACNN[74]，這是由于卷積算子的靈活性和網絡架構的簡潔性，首先構造了一個可學習的卷積權重庫，其次將即插即用的卷積算子PAConv 直接集成到一些經典點云網絡架構，包括PointNet[4]、PointNet++[5]、DGCNN[39]中，分別替換原先編碼器中的MLP 和EdgeConv，而不更改原有的網絡配置，最大程度地減少了復雜網絡架構的影響，使得PAConv的有效性大大提升.同樣，OA值僅次于PACNN 的SPCNN[73]也定義了一個可學習的卷積權重池，網絡也類似于PointNet++[5].且二者均采用自適應學習的方式，即選擇合適的基本權重矩陣和通過3D 空間中點的位置關系學習得到的相關系數向量來構造卷積核，以更好地處理不規則和無序的點云數據.不同之處在于，PAConv 采用了一個分數網絡來學習，而SPConv 通過構造幾何引導的索引映射函數來實現.相比于PACNN、SPCNN 的結果較差的原因可能還因為其網絡層次相對較深，構造了一個具有多層次結構的卷積網絡，因此復雜網絡架構雖然降低了其性能但影響不大.在今后的研究中可以選擇將PAConv或SPConv 集成到其他任務網絡中以幫助提升結果的準確性和高效性.

類似地，對比各個網絡的mAcc值可以得出目前相對較優的網絡是DPCNN[64]，這是由于該空洞點卷積顯著增加了點卷積的感受野大小，其所涉及的空洞機制也可以很容易地集成到大多數現有的點卷積網絡中.空洞卷積通過動態調整空洞率，在不丟失空間分辨率的情況下擴大卷積感受野，由此獲得多尺度信息.在未來的研究工作中，在此基礎上通過引入空洞率隨網絡深度增加而增大的動態空洞點卷積來進一步討論卷積網絡性能也可能是一個更有研究價值的方向，這樣的網絡可以在初期學習局部特征，在后期學習更高級別的信息.

3.3 點云分割

根據分割粒度可以將點云的分割任務分為部件級的部件分割、對象級的實例分割、場景級的語義分割[3]，3 者之間的區別示例如圖14 所示（來源：ShapeNet 數據集、S3DIS 數據集、SemanticKITTI 數據集）.

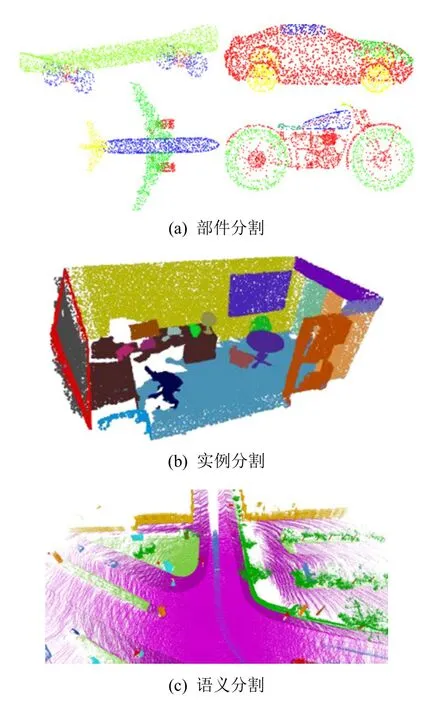
Fig.14 Comparison of point cloud segmentation tasks圖14 點云分割任務對比

具體來說，點云語義分割是根據點的語義信息把點云劃分為若干個特定的、具有獨特性質的子區域并識別出點云內容打上類別標簽的任務.不區分不同的目標，也就是將相同類別的不同目標歸為同一個標簽.與語義分割相比，點云實例分割更具挑戰性，它需要更精確和細粒度的點推理，不僅需要區分具有不同語義信息的點，而且需要區分具有相同語義信息的實例，也就是識別并區分出各個目標，歸為不同的標簽.部件分割則是區分某個實例的各個部位并打上不同的類別標簽的任務.

但由于實例分割任務在應用較少，這里不再對場景級的點云實例分割任務作進一步的分析對比研究.同樣，參考關于深度學習在點云上的研究綜述[3]，本文分別整理了相關的用于3D 點云部件分割與語義分割任務的數據集和評估指標，并在此基礎上對各個卷積網絡的性能進行了對比分析.

3.3.1 部件分割

1）數據集.為了測試不同的卷積運算在3D 點云部件分割任務中的結果，現有研究工作均使用了ShapeNet（2015）[90]這一合成數據集.ShapeNet 數據集包含了約300 萬個3D 目標物體，其子集ShapeNetCore包含了來自55 個類的51 300 個目標物體.

2）評價指標.為了評估這些卷積運算在3D 點云分割任務中的性能，現有研究工作提出的評價指標主要是均交并比（mean intersection over union,mIoU）.在每個類上計算交集和并集之比的平均值即為類均交并比（class mIoU）；在每個實例上計算交集和并集之比的平均值即為實例均交并比（instance mIoU）.

3）對比結果.表6 列舉了各個研究工作中的點云分割網絡在部件分割任務上的性能并進行了結果對比，包括輸入類型（圖像I/點坐標P/法向量N）和2 個評價指標在ShapeNet 數據集上的結果.為了更全面地對比各個卷積網絡的性能，表6 中除了列舉了基于點的卷積網絡外，還列舉了引言中提到的一些其他的有代表性的方法，包括先驅工作PointNet[4]，基于投影的方法A-CNN[16]，基于體素的方法SparseConvNet[20]和PVCNN[22]，基于晶格的方法SPLATNet3D[25]、SPLATNet2D-3D[25]和SFCNN[26]，基于圖的方法SPH3D-GCN[43].

4）結果分析.部件分割任務最大的難點就是具有相同語義標簽的實例具有較大的幾何變化和模糊性.對比各個網絡的class mIoU 值，可以得出目前相對較優的網絡是Ψ-CNN[61]，其所使用的卷積算子Spherical Convolution 是目前性能較好的.Ψ-CNN[61]著重研究分析了不同的點局部鄰域搜索策略.顯然，對于不同結構的點云，應該采取不同的點局部鄰域搜索策略，例如球查詢、K近鄰、樹結構（kdtree,octree）.相比之下，球查詢、K近鄰是直觀的、簡單的，但對于點數更多的輸入點云，樹結構顯然是更有效的，因為點的局部鄰域信息更容易獲得，這就提升了Ψ-CNN[61]的計算效率.如果點云是稀疏的，分布很廣泛且沒有規律可循，如某個真實場景，kdtree 能更好地劃分物體與背景，而octree 則很難決定最小立方體的尺寸應該是多少，太大則一個立方體里可能有很多不同標簽的點云，太小則可能立方體之間關聯不起來.如果點云分布非常規整且聚集，如某個特定物體，則octree更容易求解凸包，并且點與點之間相對距離無需再次比對父節點和子節點，更加明晰.因此，Ψ-CNN[61]這一基于八叉樹結構的網絡，可以更高效地探索物體各個部件的幾何信息和幾何變化，具有相對更優的網絡性能和對比結果.

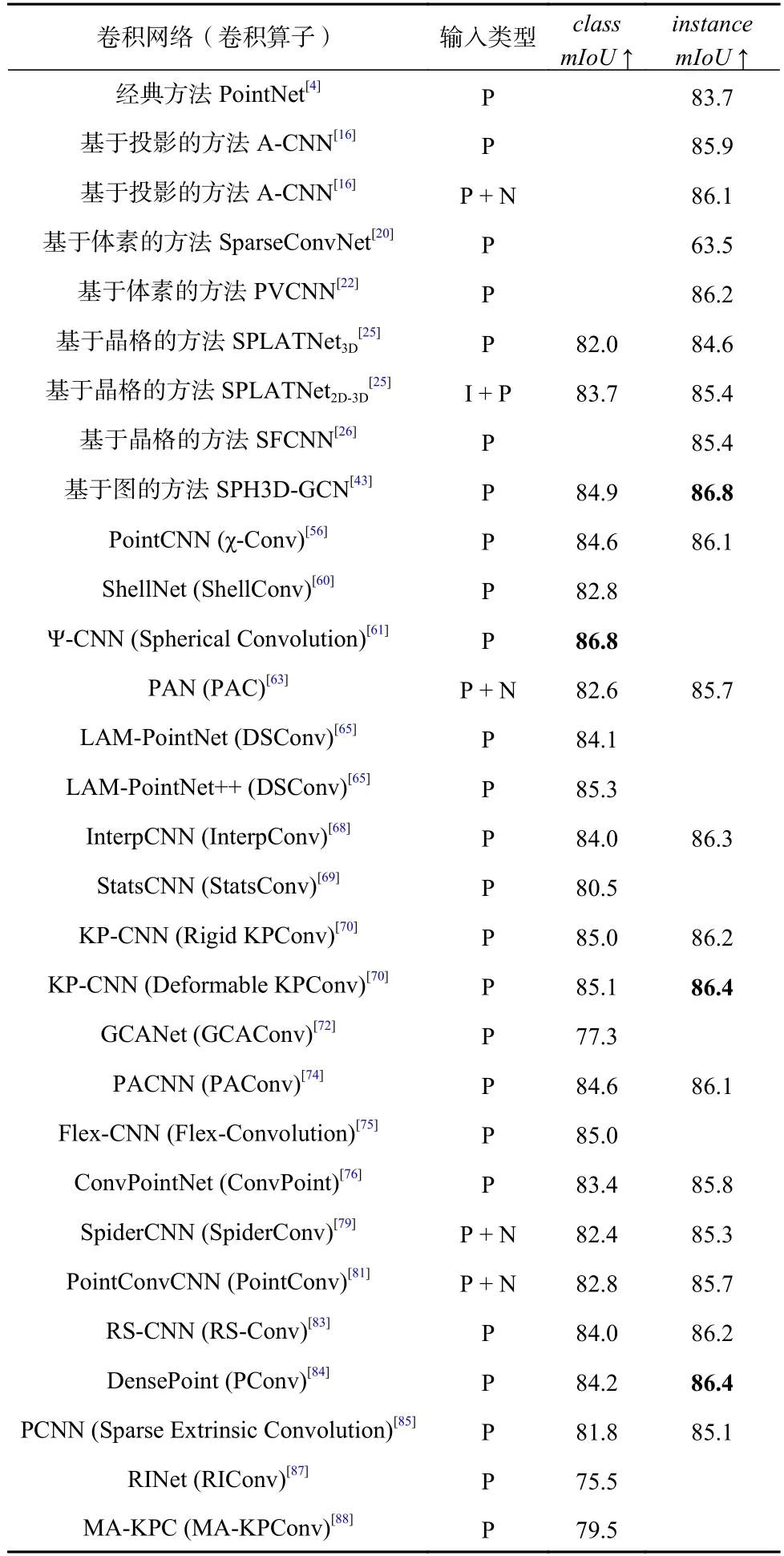
Table 6 Comparison Results of Part Segmentation Networks' Performances on the ShapeNet Dataset表6 部件分割網絡性能在ShapeNet數據集上的對比結果%

類似地，對比各個網絡的instance mIoU 值，可以發現，基于圖的方法SPH3D-GCN[43]要普遍優于其他方法，這是由于離散核、可分離球卷積和基于圖的體系結構的結合增加了該方法的可擴展性和靈活性，增加了網絡的性能.其中，采用不同的離散核可以識別相同鄰域的不同特征；引用可分離球卷積策略分別執行深度卷積運算和點卷積運算，顯著減少了網絡的參數數量和計算成本；使用更靈活的基于圖的體系結構設計網絡架構，保證了網絡在更接近標準CNN 的同時還能更好地處理大規模點云數據，計算效率較高.因此，除了直接處理離散點數據的卷積網絡，處理圖數據的卷積網絡也是研究人員傾向于深入研究的方向.此外，KP-CNN[70]是基于點的卷積方法中相對較優的，其中，可變形KPConv 的性能較剛性KPConv 的性能要稍好一些，這是由于可變形KPConv具有更強大的點特征描述能力以及可學習性.

3.3.2 語義分割

1）數據集.語義分割一般用于真實場景中進行場景與物體之間的分割任務，將目標與背景之間進行分割.現有的較為常用的真實場景數據集（realworld datasets）均是由不同類型傳感器獲取得到的.這里列舉并比較了4 個在點云分割任務研究中使用較多的真實場景數據集，如表7 所示.與合成數據集不同的是，這類數據集由于傳感器本身固有的物理特性限制、掃描過程中的路線或位置限制（如建筑物的頂部），最終得到的點云會有不同程度的遮擋、空洞和噪聲，因此訓練和測試的難度較合成數據集來說要大很多，是極具挑戰性的.

2）評價指標.為了評估這些卷積運算在3D 點云分割任務中的性能，現有論文提出了不同的評價指標，常用的性能指標主要包括OA和class mIoU.

Table 7 Common Real-World Datasets表7 常見的真實場景數據集

3）對比結果.表8 列舉了各個研究工作的點云分割網絡在不同數據集的語義分割任務上的2 個評價指標的對比結果，由于在SemanticKITTI 數據集上的結果較少，故這里不展開分析.同樣，為了更全面地對比各個卷積網絡的性能，表8 中除了列舉了基于點的卷積網絡外，還列舉了引言中提到的一些其他的有代表性的方法，包括先驅工作PointNet[4]和PointNet++[5]、基于投影的方法A-CNN[16]、基于體素的方法PVCNN 和PVCNN++[22]、基于圖的方法SPH3DGCN[43].

4）結果分析.從表8 中可以看出，HIGCNN[67]在室內數據集S3DIS 和室外數據集SemanticKITTI 上均取得了相對較優的class mIoU值，該網絡最顯著的特點是輕量級，采用較少的參數，消耗較低的計算成本和內存成本，充分挖掘點云的細粒度幾何特征，自適應地進行特征選擇，增強有用的結構特征和抑制無用的噪聲特征，在保證獲得更好性能的同時復雜度更低、準確性更高.

卷積算子ConvPoint[76]在室內數據集S3DIS 和室外數據集Semantic3D 上均取得了相對較優的OA值，該卷積方法是稀疏化和非結構化數據在離散卷積上的推廣方法，具有靈活性和計算效率高的特點，其中，各個點和卷積核元素之間的幾何關系是相對的，由此降低了對輸入點云大小的敏感性，可以構建各種網絡體系結構.

此外，KP-CNN[70]在室內數據集ScanNet 上取得了相對較優的class mIoU值，在室外數據集Semantic3D上取得了次優的class mIoU值.從數據集上來看，這些真實場景數據集中的3D 場景范圍較大，因而無法作為一個整體進行分割任務.而KP-CNN[70]采用隨機選取的球體來將一個整體場景點云分割成多個子云（subclouds），確保每個點都由不同的球體預測多次，這就保證了每個點的預測概率是平均的.通過計算每個輸入點對不同位置的KPConv 層輸出結果影響相對于輸入點特征的梯度，即有效感受野（effective receptive field,ERF），可以發現，剛性KPConv 的ERF對每種類型的對象都有相對一致的度量范圍，而可變形KPConv 的ERF 具有更強的自適應性，可以適應不同類型對象的大小，提高了網絡適應場景的幾何結構的能力，并能夠從場景中獲取更多的細節信息，其在室內數據集S3DIS 上具有更好的性能.然而在更具多樣性對象更豐富的室內數據集ScanNet 和室外數據集Semantic3D 上，剛性KPConv 的性能較可變形KPConv 的性能要稍好一些，這是由于可變形KPConv在提升了點特征描述能力的同時會增加整個網絡的復雜性，可能會干擾網絡的收斂或導致過擬合.

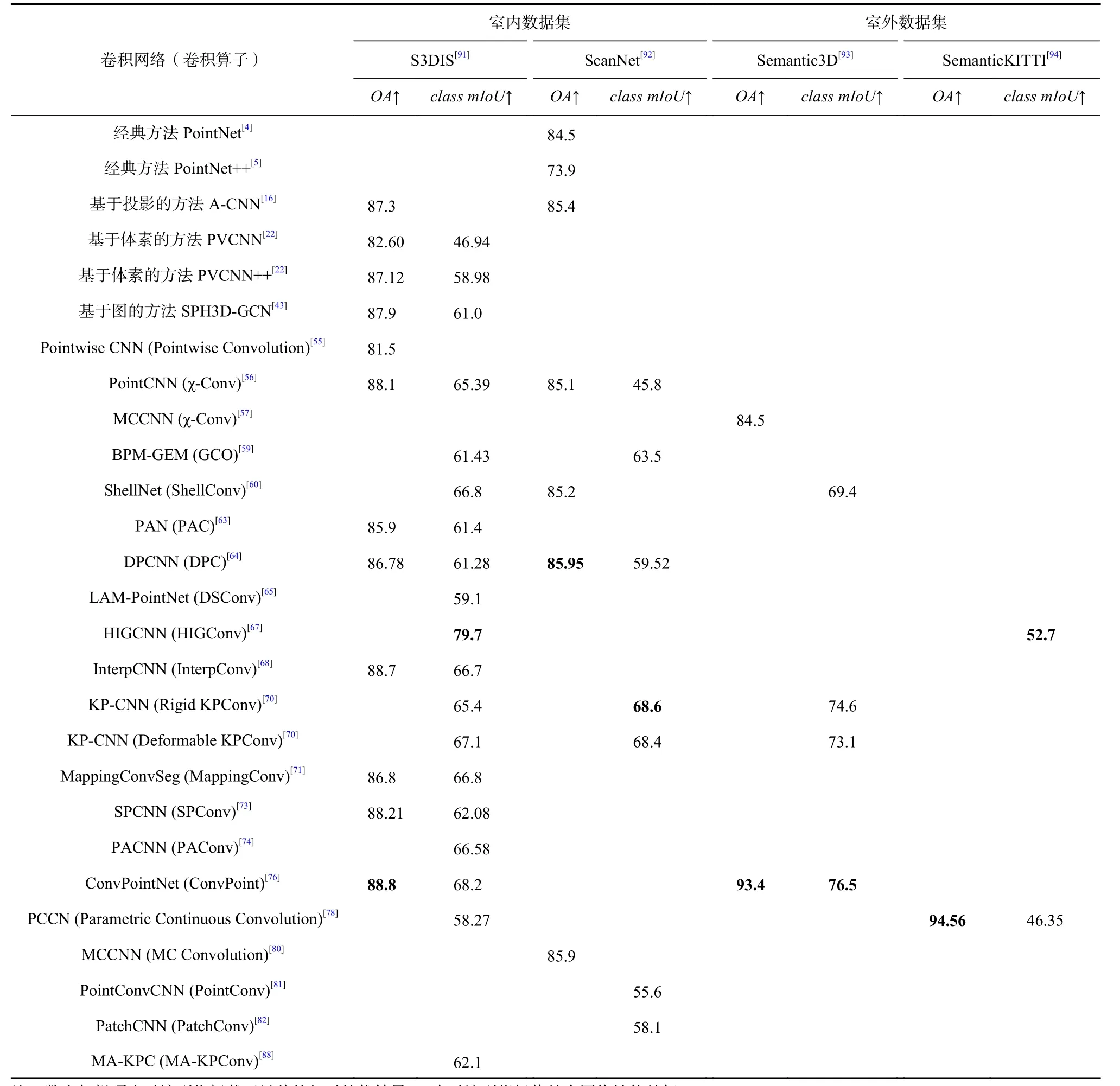
Table 8 Comparison Results of Semantic Segmentation Networks' Performances表8 語義分割網絡性能對比結果 %

3.4 法線估計

表面法線是3D 點云的重要屬性之一，在很多領域都有大量應用，例如，在進行光照渲染時產生符合可視習慣的效果時需要表面法線信息才能正常進行.大部分點云任務的處理也都要用到法線，包括點云平滑濾波、點云配準、點云曲率計算等.此外，估計一個點云的表面法線是3D 重建任務的一部分[85]，性能優劣將直接影響到后續的重建結果.

表面法線估計任務可以看作是一個有監督的回歸問題，近似于估計表面某個相切面的法線，需要對每個點進行預測.因此，也可以通過改變點云分割網絡的一些超參數來適應這項任務.

本文將涉及法線估計的研究工作進行了對比分析，結果如表9 所示，采用的數據集是ModelNet40[89]，對比的性能指標是余弦損失（cosine loss）.同樣，為了更全面地對比各個卷積網絡的性能，表9 中除了列舉了基于點的卷積網絡外，還列舉了引言中提到的一些其他的有代表性的方法，包括先驅工作PointNet[4]和PointNet++[5].

由表9 可以得出，對于法線估計任務，相對性能較優的卷積網絡和算子是SPCNN（SPConv）[73]，該卷積方法通過幾何引導權重選擇來推廣圖像卷積，自適應地劃分點云中的幾何學習空間.圖像像素排列規則，因此權重和像素具有確定的索引對應關系.然而，對于不規則地分布在連續3D 空間中的3D 點云，這些索引對應關系是未知的.因此，該研究工作構造了一個幾何引導的索引映射函數，該函數隱式地在卷積權重和鄰域中的一些局部區域之間建立對應關系，學習自適應地劃分并感知點云的局部幾何結構，高效地用于點云分析任務中.

Table 9 Comparison Results of Normal Estimation Task on ModelNet40 Dataset表9 ModelNet40 數據集上的法線估計任務對比結果

最后，綜合分析形狀分類、部件分割和語義分割這3 類有代表性的點云任務.在這3 類云任務中均進行了實驗和分析的研究工作，主要包括：PointCNN（χ-Conv）[56]，ShellNet（ShellConv）[60]，PAN（PAC）[63]，Interp-CNN（InterpConv）[68]，KP-CNN（Rigid KPConv）[70]，KPCNN（Deformable KPConv）[70]，PACNN（PAConv）[74]，Conv-PointNet（ConvPoint）[76]，PointConvCNN（PointConv）[81]，MA-KPC（MA-KPConv）[88]，對比結果如圖15 所示.

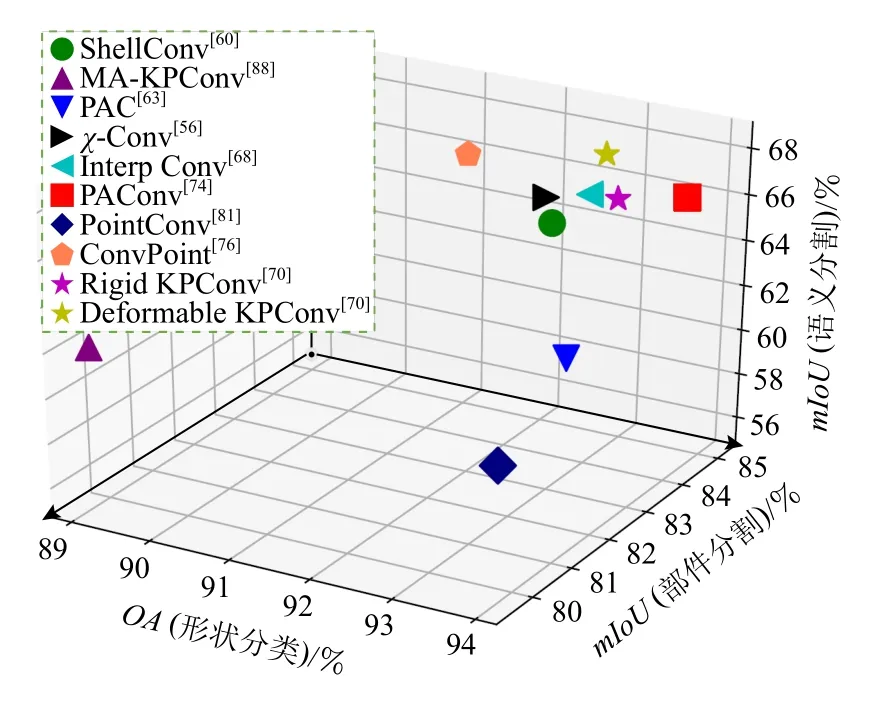
Fig.15 Comparison results of three point cloud tasks圖15 3 類點云任務的對比結果

結合表5、表6、表8 的對比結果可以得出，相對較優的結果均為連續卷積中構造虛擬化輔助信息的卷積算子，包括在點云分類任務中的PAConv[74]、在點云分割任務中的KPConv[70]、在點云法線估計任務中的SPConv[73].相比較而言，KPConv[70]這一即插即用卷積算子在今后的研究中可作為集成到各種點云任務網絡中的首選，如MA-KPC[88]，雖然對比結果顯示該網絡在KPConv[70]上進行的改進性能并沒有提升，但其研究重點在于解決點云的旋轉不變性問題，且實驗表明通過任意角度的旋轉所得到的結果均是最優的，同時，MA-KPC 是首個在S3DIS 這一大型室內場景數據集的分割任務中進行旋轉不變性問題的研究并得到了較優的結果的網絡，雖然，許多真實場景由于重力定向（gravity-oriented）原因只能繞z軸自由旋轉，整個場景的任意角度旋轉可能沒有實際應用價值，但場景中的某些小型目標可以進行任意旋轉，例如掉落在地上的物體，雖然不常見，但在實際應用中可能會影響分析結果.今后的研究還可以針對MA-KPC 所面臨的其他困難與挑戰繼續深入.

4 總結與展望

卷積運算的核心在于對特征的局部聚合和學習，經過近些年的不斷發展，通過大量的實驗分析與對比，各種各樣卷積運算和卷積網絡的提出在理論上和實踐上都被證實其是處理不規則數據格式的一種有效方法和框架.本文全面概括和提煉了近年來研究工作中提出的各種各樣新穎的可直接作用于點云上的卷積算子，分類并分析了這些卷積算子的結構和卷積運算的原理.同時，針對研究工作中所涉及到的集成了這些卷積算子的基礎任務網絡，包括點云分類網絡和點云分割網絡，從設計的網絡結構、采用的公開數據集、使用的評價指標等方面進行了分類整理與性能對比，總結了相對較優的卷積算子和卷積網絡，以助力一些下游的點云任務，如3D 目標檢測與跟蹤、3D 場景與目標分割等.雖然，卷積運算具有一定的優勢，但目前仍然存在一定的不足和待完善之處.此外，本文探討并列舉了3 個關于基于點的卷積運算的一些未來可能的研究方向，主要包括針對特殊點云應用的研究、針對不同點云任務的研究、針對不同融合方法的研究，如圖16 所示.

4.1 針對特殊點云應用的研究

1）不平衡點云數據

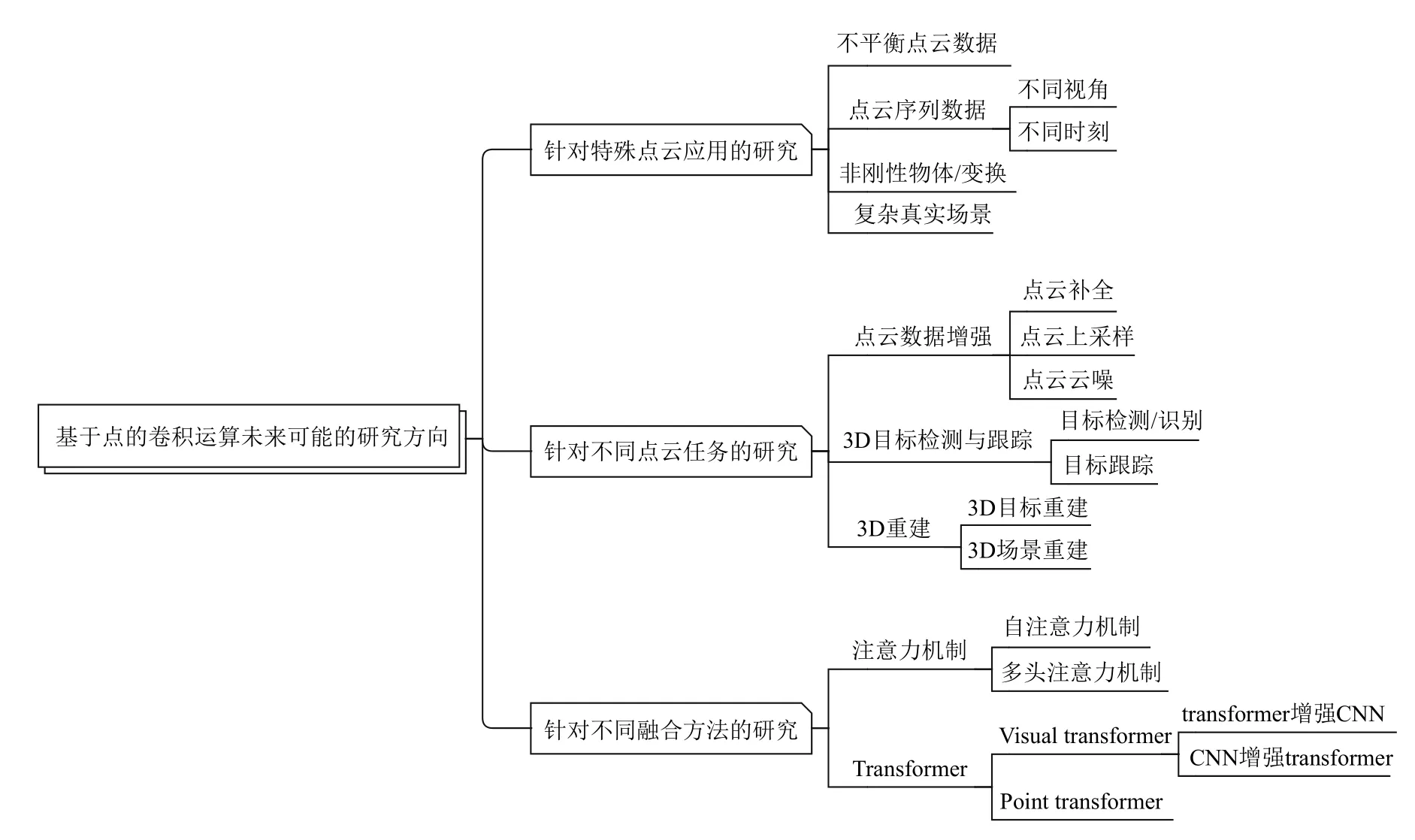
Fig.16 The future research directions of point-based convolution operations圖16 基于點的卷積運算的未來研究方向

從第3 節不同任務的OA值和mAcc/mIoU值的比較結果可以發現，盡管一些方法[70,76]都取得了顯著的總體效果，但它們在類別相對較少的情況下表現仍然有限.基于類別不平衡的點云數據的特征學習仍然是點云任務（尤其是分割任務）中一個具有挑戰性的問題.

2）點云序列數據

一些實際應用場景中有時需要對3D 傳感器在不同視角或不同時刻下捕獲的點云序列數據進行處理，如動作捕捉、3D 重建.①不同視角的點云序列.利用不同視角點云之間的點匹配估計運動物體在3D 空間中的變換關系，包括旋轉、位移.②不同時刻的點云序列.利用不同時刻點云之間的特征匹配估計運動物體在3D 空間中的運動信息，包括速度、角速度、動量等.這2 個匹配估計流程通常包含2 個基本步驟：局部特征描述和全局特征匹配.因此需要網絡具有一定的鑒別能力來區分相同目標物體內部或不同目標物體之間的局部幾何結構.這就對特征提取和特征匹配提出了更高的要求.然而，現有的提取點云局部和全局特征的方法仍難以充分滿足這類需求，而且對于原始數據和應用場景的變化較為敏感.因此，這也是今后的一個重要的研究方向，且具有重要的實際應用價值.

3）非剛性物體/變換

剛性物體（rigid body）發生的剛性變換是平移和旋轉，而相比于剛性物體，非剛性物體（non-rigid body）就是會發生形變（即伸縮、仿射、透射等比較復雜的非剛性變換）的物體.對于非剛性3D 模型，點的坐標特征受姿態變化（pose variation）和非剛性變換（nonrigid deformation）的影響，因此局部的變化對網絡的性能要求較高.目前在圖像中的非剛性物體研究比較廣泛[95]，因此結合基于點的卷積算子進行非剛性點云物體的局部特征提取和相關任務研究也是一個較為新穎的方向.

4）復雜真實場景

在許多實際應用中，傳感器獲取的點云通常是大規模的且較為復雜的，例如目前自動駕駛領域研究使用最廣泛的KITTI 數據集[96].但大多數現有方法都適用于小型點云數據（點數較少），在大型點云數據上的效果較差.因此有必要進一步研究適合在大規模點云任務上應用的卷積算子和卷積網絡，進一步在降低計算復雜度的同時提升算法性能.

4.2 針對不同點云任務的研究

本質上，卷積網絡中的卷積運算就是特征提取的過程，由于點云數據的特殊性，而產生了各種各樣的可作用于點云上的卷積算子進行卷積運算，由于其即插即用的特性，這樣的卷積算子除了用于點云分類、分割網絡以外，還可以用于其他的需要進行特征提取的網絡.

1）點云數據增強

實際上，許多3D 掃描設備直接獲取的點云數據質量會受到很多因素的影響，例如物體之間的遮擋、掃描精度降低、掃描過程中的路線或位置限制等，可能產生質量較差的點云，存在空洞、稀疏、離群點和噪聲點等.因此，點云補全（point cloud completion）[97]、點云上采樣（point cloud upsampling）[98]、點云去噪（point cloud denoising）[99]等點云數據增強任務也是研究的一個熱點，將這些基于點的卷積算子集成到這些特定點云任務的網絡中用于特征提取也是一個研究方向.例如，可以將具有旋轉不變性的卷積算子集成到點云補全任務的網絡中，通過多個維度的旋轉及特征提取，對點云進行多個角度的補全，從中選擇最優的補全結果.

2）3D 目標檢測與跟蹤

點云分類、分割任務是3D 目標檢測/識別、3D目標跟蹤等更復雜且重要的下游任務的基礎.典型的技術路線一般包括：目標分類/分割（對前景與背景進行分類，將背景剔除）→目標檢測/識別（定位目標，確定目標位置及大小；定性目標，確定目標類別）→目標跟蹤（追蹤目標的運動軌跡）.在這一過程中，特征提取占據很重要的部分，將這些卷積算子集成到這些特定任務的網絡中用于高維特征提取也是一個研究方向.相關領域的應用有：在機器人領域的動作捕捉及位姿估計；在自動駕駛領域的障礙物識別與避碰；在國防領域的精準目標打擊.

3）3D 重建

點云的特征提取是3D 目標重建、3D 場景重建等更復雜且重要的點云任務的一部分.一個具體的3D 重建過程主要包括點云數據預處理、分割、三角網格化、網格渲染.實現高精度、高效率的點云3D重建也是今后重要的研究方向之一.相關領域的應用有：在遙感領域的特殊場景（如地形）的拼接及重建；在文化遺產保護領域的古文物數字模型庫（如故宮數字博物館）的恢復與構建.

4.3 針對與不同方法融合的研究

除了卷積運算外，還有很多方法已成功用于3D點云數據處理中，例如，注意力機制、Transformer.將它們各自的優勢與基于點的卷積算子進行結合也是今后研究的一個趨勢.

1）注意力機制

卷積運算在捕獲局部特征方面有很強的優勢，但在全局范圍建模方面效率很低.相比之下，注意力機制可以有效地模擬特征之間的全局范圍關系，但存在過度平滑問題[100].因此，將二者結合得到的注意力卷積[62-64]可以更好地在全局信息聚合（注意力）和局部信息建模（卷積）之間建立某種聯系.同時，采用不同的變體機制，如自注意力機制（self-attention mechanism）、交叉注意力機制（cross-attention mechanism）、多頭注意力機制（multi-head-attention mechanism）等，與基于點的卷積運算的結合也是今后可以研究的一個方向.

2）transformer

transformer 是一種基于注意力的編碼器-解碼器架構，最近在機器視覺領域引起了人們極大的研究興趣.與傳統的深度學習網絡相比，transformer 架構層次容易加深且具有更小的模型偏差，通常以自監督方式在大量訓練數據上對模型進行預訓練，有助于模型學習通用表征，進而針對下游任務在較小的數據集上進行微調.受到自然語言處理（natural language processing,NLP）領域中基于transformer 的預訓練方法[101]可以顯著提升性能的啟發，計算機視覺領域的研究人員也提出了視覺transformer（visual transformer,ViT）[102]用于各類視覺任務（如分類、分割）中.一項研究表明transformer 在理論上具有比CNN 更強大的建模能力[103].然而，它的計算成本也隨著特征分辨率呈二次方增長.一些研究工作嘗試通過transformer 和CNN 的組合方法解決這一問題（如 BoTNet[104]，DeiT[105]，ConViT[106]，CeiT[107]等 ）.①transformer 增 強CNN：將transformer 插 入CNN 主干或替換部分卷積運算.②CNN 增強transformer：利用適當的卷積偏差來增強transformer 并加速其收斂.

同時，transformer 模型特別適合于處理不規則的點云數據，因為transformer 的核心即自注意力算子本質上是一個集合算子，它對輸入元素的排列和基數是不變的，而點云本質上是不規則地嵌入在3D 空間中的集合.因此，有研究工作為各種點云任務構建了Point transformer 網絡[108]，將自注意力算子應用在每個點周圍的局部鄰域以及點云網絡中位置信息的編碼.類似地，如何更高效、更魯棒地將transformer 和基于點的卷積運算相結合并應用到點云任務中也是未來的一個研究熱點.

總之，隨著越來越多對3D 掃描設備的普及和對3D 點云數據的關注，現有的卷積算子和網絡可以解決一些點云處理相關的問題并得到較優的結果，但還有進一步提高和改進的空間.在未來的研究道路上，還可能有更多原理簡單、訓練高效、性能優異的卷積算子和卷積網絡相繼被提出，這會是在3D 視覺領域中未來很長一段時間內的研究熱點.

作者貢獻聲明：韓冰提出寫作命題，收集和調研文獻，完成論文撰寫與修改；張鑫云提出修改意見；任爽指導論文撰寫.