多尺度模擬計算方法在超高溫高熵陶瓷材料中的應用進展

魯 楠 何鵬飛 種曉宇 胡振峰 梁秀兵

（1 國防科技創新研究院，北京 100071）

（2 昆明理工大學材料基因工程校重點實驗室，昆明 650093）

0 引言

受高熵合金材料設計理念的啟發，美國北卡羅來納州立大學STEFANO 團隊［1］于2015年首次成功制備出（Mg0.2Co0.2Ni0.2Zn0.2Cu0.2）O 氧化物高熵陶瓷，自此掀起了高熵陶瓷材料的研究熱潮［2］。高熵陶瓷材料體系也由最初的氧化物擴展到碳化物、硼化物、氮化物、碳氮化物等多種材料體系［3-8］。而以難熔金屬碳化物、硼化物超高溫陶瓷為組元的超高溫高熵陶瓷材料，由于其具有較高的熔點、優異的高溫強度、良好的熱穩定性以及較低的熱膨脹系數等特性，在極端苛刻服役環境下展現著巨大的應用潛力，已成為高熵陶瓷領域研究的熱點方向之一［9-13］。

與傳統材料相比，超高溫高熵陶瓷材料研究往往涉及陽離子、陰離子、缺陷多組元復雜成分空間，涉及宏觀、介觀、微觀、納觀多個尺寸維度，涉及極端熱、力等多場耦合服役環境，研究工作更為復雜［4-6，14］。此外，捕捉超高溫高熵陶瓷材料的微觀結構細節、特征和服役性能特點需要大量的實驗和數據作為支撐，表征測試手段也需要不斷的創新［15］。因此，面對復雜成分空間的超高溫高熵陶瓷材料，依賴科學直覺與經驗試錯的傳統研究方法開發高性能超高溫高熵陶瓷材料盲目性過大、研發與應用周期過長、效率過低［15-16］。

近年來，隨著計算機、大數據和人工智能技術的發展，以計算模擬、數據分析、機器預測等輔助手段為代表的材料計算研究方法初步形成，材料科學已逐步從經驗科學走向理性科學［15］。材料集成計算通過建立物理模型引導材料成分及結構設計，依靠多尺度模擬計算預測材料設計對其性能和可靠性的影響，優化工藝模型以獲得微觀結構等制造工藝參數，最后通過數據分析處理實現材料的并行設計和快速開發［16-25］。因此，材料集成計算技術不僅能夠大幅度減少超高溫高熵陶瓷材料研發過程中重復性、試錯性工作，也能夠加速材料研究過程中的理論創新，從而加快超高溫高熵陶瓷材料的研發與應用進程。

本文首先簡要介紹具有代表性的多尺度材料計算方法，進而綜述多尺度材料計算方法在超高溫高熵陶瓷研究中的典型應用成果，最后對多尺度材料計算方法在超高溫高熵陶瓷研究中的前景進行展望。

1 多尺度材料計算方法

多尺度材料計算方法是進行高通量建模、集成計算及數據處理分析的基礎［16，26］。目前，比較有代表性的多尺度材料計算方法主要有第一性原理計算、分子動力學模擬、相圖計算法、機器學習等。

1.1 第一性原理計算（First-principles Calculations）

第一性原理計算是從構成物質的原子角度，不依賴任何經驗和半經驗參數，通過求解薛定諤方程（Schr?dinger equation），預測材料體系的電子結構、穩定性、總能量和各種物理、化學性質［6，27］。密度泛函理論（Density Functional Theory，DFT）是通過量子力學尋找電子、原子核與其運動之間關系的模擬計算方法，廣泛應用于研究材料的物理化學性能［28］。目前，基于密度泛函理論的第一性原理計算是微觀原子尺度材料計算學中最主要且最關鍵的方法之一，其理論基礎就是多電子系統的定態薛定諤方程［6，16，29-31］：

式中，為哈密頓量算符，Ψ為波函數，表示所有電子的坐標集合，表示所有原子核的坐標的集合。

由于很難求解多電子系統的薛定諤方程的精確解，密度泛函理論通過絕熱近似和單電子近似，把多電子系統的薛定諤方程轉化為單電子有效勢方程［6，16，29-31］：

式中，

即將每個電子的運動行為描述成單個電子在一個有效勢場Veff()中的獨立運動。有效勢包含了原子核對電子的靜電吸引作用、電子間的庫倫相互作用和交換關聯作用。其中，不確定項為電子間的庫倫相互作用和交換關聯作用。進一步基于Hohenberg-Kohn定理通過變分原理可得到Kohn-Sham方程［6，29-31］：

式中，第一個勢能項V()指一個電子與所有原子核之間的相互作用，第二個勢能項VH()稱為Hatree 勢能，為一個電子與所有電子所產生的庫倫排斥作用，第三個勢能項VXC()為交換關聯勢。

在實際計算中Kohn-Sham 方程是通過自洽迭代過程求解的，所以無法準確計算交換關聯勢。在基于密度泛函理論的第一性原理計算中，所有的近似都被歸結到交換關聯勢這一項上，所以計算的精度直接由交換關聯勢泛函的近似形式決定。交換關聯勢通常采用局域密度近似（Local Density Approximation，LDA）和廣義梯度近似（Generalized Gradient Approximation，GGA）進行處理［28］。局域密度近似認為交換關聯勢只與局域的電子密度有關，形式簡單。廣義梯度近似則考慮了空間電子密度的不均勻性，在描述非均質系統的交換關聯勢更為準確。目前基于密度泛函理論進行第一性原理計算的軟件非常多，比較常見的有基于贗勢-平面波方法的Vienna Ab initio Simulation Package （VASP）、CASTEP、Quantum ESPRESSO、Abinit，基于數值原子軌道基組的SIESTA、ABACUS等［27］。

針對超高溫高熵陶瓷材料，基于密度泛函理論的第一性原理計算可根據材料體系組成原子結構特征，近似處理體系中電子間的交換關聯作用，不僅能夠獲得材料的電子態密度、晶格畸變等內部結構信息，而且能夠預測材料的機械、熱物理等性能［15-16］，篩選出具有目標性能的成分體系，提高超高溫高熵陶瓷材料的研發效率。一般基于密度泛函理論的第一性原理計算程序的計算時間與材料系統的尺寸的三次方成正比。受限于計算機的處理能力，目前能夠處理的材料體系相對較小［15-16］。

1.2 分子動力學模擬（Molecular Dynamics Simulation）

分子動力學模擬是在原子、分子水平上基于經典牛頓力學獲得體系的熱力學及其他宏觀性能的計算模擬方法，已廣泛應用于醫藥、化學、生物和材料等多個領域［32-34］。分子動力學模擬認為體系內的所有粒子均在其他粒子提供的勢場中遵循牛頓運動方程隨時間演化［15-16］。這種由粒子間相互作用構成的勢場通常采用函數形式進行描述，即勢函數。勢函數的選取直接決定了分子動力學模擬計算結果的準確性和可信度。目前已經發展了多種形式的勢函數，比較常見的有對勢、無方向多體對泛函數、考慮角度效應多體勢等。對于平衡態分子動力學模擬，體系的宏觀物理量是一切可能的微觀狀態的系綜平均，依據統計力學中的各態歷經假設，體系將經歷一切可能的微觀態，則系綜平均就可以相應地用時間平均來代替。目前使用范圍最廣的分子動力學模擬軟件是由美國Sandia 國家實驗室支持開發的LAMMPS （Large-scale Atomic/Molecular Massively Parallel Simulator）。LAMMPS 不僅支持氣、液或固態、各種系綜下的原子分子體系模擬，支持多種勢函數，而且具有良好的并行擴展性［15-16］。

分子動力學模擬能夠直接模擬粒子在空間中隨時間演化的運動軌跡，因此可以直觀地處理材料體系的動力學問題，并能夠預測各種動力學相關的物理化學性質，如模擬相變、變形、擴散等過程。對于以極端苛刻環境服役需求為導向的超高溫高熵陶瓷材料，其超高溫力學、氧化、燒蝕等服役性能對其應用至關重要，但極端環境下的性能測試周期長、成本昂貴。基于分子動力學模擬，不僅可以預測超高溫高熵陶瓷材料的超高溫力學及熱物理性能，而且能夠揭示其在極端環境下的氧化燒蝕機制，對具有優異耐極端環境能力的超高溫高熵陶瓷材料設計及優化具有重要意義［13-14］。受限于計算機的運行速度和存儲能力，分子動力學模擬計算的材料體系規模較小，原子數較少，缺乏普遍性，且目前構建強關聯電子體系精確的勢函數難度較大，限制了分子動力學模擬方法更為廣泛的應用［15-16］。

1.3 相圖計算法（Calculation of Phase Diagram，CALPHAD）

CALPHAD 基于熱力學基礎理論及熱力學數據庫，以實驗、第一性原理計算等方法獲得的數據，構建各相的熱力學模型，通過吉布斯自由能建模及相平衡計算獲得多元多相材料的相圖［35-36］。CALPHAD法以溫度T、壓力P、組元n為基本變量構筑體系的吉布斯自由能模型，總的吉布斯自由能由常壓下的自由能和壓力貢獻的自由能兩部分組成，即［16，37-38］：

式中，P0為常壓，ni為第i個組元，忽略第二項則可直接計算常壓下材料的熱力學性質。當只考慮二元交互作用時，多組元固溶體相α的吉布斯自由能可以表示為［16，37-38］：

式中，xi和xj分別為組元i和j的摩爾分數，Gα i為組元i的摩爾吉布斯自由能，第二項為理想混合熵對吉布斯自由能的貢獻。前兩項描述了理想溶液的吉布斯自由能，當實際體系偏離理想溶液，必須采用式中第三項——過剩摩爾自由能進行修正。過剩摩爾自由能常采用Redlich-Kister 多項式［39］表示，其中L為二元交互作用參數，可以取0～m級參數。當壓力影響不可忽略時，需確定狀態方程（Equation of state，EOS），并構建吉布斯自由能函數，再根據高壓范圍的實驗數據擬合優化壓力模型中的所有參數。近些年來，通過擬合優化原子移動性參數或各類擴散系數，CALPHAD 法已向全溫域、極高壓范圍擴展，數據庫也開始涉及密度、熱膨脹系數、熱導率等物理性質。

將第一性原理計算與CALPHAD 法結合，一定程度上能夠擺脫實驗條件、經驗公式的限制，且第一性原理計算得到的晶格常數、結合能、混合焓等信息可為CALPHAD 建模提供理論數據支持。目前，通用的相圖計算軟件有Thermo-Calc、FactSage、Matcalc、Pandat 等，其中Thermo-Calc 軟件可以處理多組元系統，廣泛應用于各種熱力學計算中［40］。對于超高溫高熵陶瓷材料而言，CALPHAD 法有利于更準確地理解材料在升降溫過程中的相變，并可為超高溫高熵陶瓷材料的工藝設計提供理論依據。

1.4 機器學習（Machine Learning）

機器學習，作為人工智能的一個分支，是通過數據挖掘方法尋找數據之間的潛在聯系。機器學習特別適合處理高度復雜的且具有非線性輸入/輸出關系特征的數據［6］。在材料科學領域，由于通過實驗和計算模擬得到的數據通常都具有多因子、多噪聲、非線性和非高斯分布等特點，并且各種屬性之間通常都具有一定的相關性，這使得經典的統計方法和模型用于材料領域數據分析時具有一定的局限性。機器學習技術由于在解決回歸、分類和排序等基礎問題時具有良好的效果，已經成為很多領域智能數據分析的重要工具，這使得它可以成為解決材料領域各類數據分析問題的新途徑。

超高溫高熵陶瓷材料不僅涉及多相、多組元的復雜成分空間，納觀、微觀、介觀、宏觀多個尺度維度，而且涉及熱、力、化學等多場耦合服役環境，通過計算模擬和實驗獲得的數據高度復雜，難以采用經典統計方法進行處理分析。將第一性原理等材料模擬計算方法與機器學習方法相結合，構建超高溫高熵陶瓷材料成分-結構-性能之間的映射關聯，可有效縮小超高溫高熵陶瓷成分候選空間，形成超高溫高熵陶瓷成分設計準則，快速高效地指導超高溫高熵陶瓷材料設計及研發。

2 多尺度材料計算方法在超高溫高熵陶瓷材料中的典型應用成果

面對復雜成分空間的超高溫高熵陶瓷材料，采用多尺度材料計算方法能夠實現材料成分/結構/性能的高效篩選，顯著提高超高溫高熵陶瓷材料的研發效率［16，26］。本文從以下幾個方面介紹了多尺度材料計算方法在超高溫高熵陶瓷材料中的典型應用成果。

2.1 成分預測

2.1.1 高熵陶瓷形成能力

建立超高溫高熵陶瓷單相形成能力判據，可為超高溫高熵陶瓷材料的設計及相穩定性的預測提供初步的理論指導［11］。美國杜克大學STEFANO 教授等［41］人提出了熵形成能力（Entropy Forming Ability，EFA）的概念，EFA 是通過測量給定晶胞大小的結構隨機化計算的能量分布譜來預測形成高熵單相固溶體的能力，單位為（eV/atom）-1。能量分布譜越寬，將結構無序引入到系統中所需的能量越大，EFA 值越低。因此，EFA 提供了一種無序化合物相對可合成性的量度，EFA 值越大，形成單相固溶體的可能性越高，體系相對越穩定［11，41］。

STEFANO 教授等［41］人首先計算了由8 種難熔元素（Hf、Nb、Mo、Ta、Ti、V、W 和Zr）構成的56種五金屬組元的EFA值，并選取了9種五金屬組元碳化物進行實驗驗證，實驗結果與EFA 預測結果吻合，如圖1所示。進而，該團隊與加利福尼亞大學圣迭戈分校Vecchio 教授合作，采用機器學習方法預測了含Cr 元素的70 種新組分的EFA 值，證實了該方法可在巨大成分候選空間進行有效篩選［42］。但目前EFA 計算只針對五組元難熔金屬碳化物，無法對其他體系的超高溫高熵陶瓷材料進行預測，局限性較大；而且存在EFA 值低于50（eV/atom）-1仍能形成均質單相固溶體的材料體系，預測準確性有限［11］。

圖1 9種五元金屬碳化物不同結構的能量分布及XRD圖譜［41］Fig.1 The energy distribution and X-ray diffraction pattern of different configurations of 9 kinds of five-metal carbides［41］

2.1.2 相組成

材料相圖包含熔點、相轉變點、相共存區等材料熱物理信息。相圖計算能夠預測超高溫高熵陶瓷材料的相組成、單相固溶體形成溫度，進而有效地指導超高溫高熵陶瓷材料的工藝設計。中國科學院蘭州物化研究所孟軍虎團隊［43］基于高熵合金熱力學數據庫（TCHEA3），采用Thermo-Calc2019a 軟件計算了（VNbTaMoW）0.5Cx體系的相圖，如圖2所示。該相圖計算結果表明，（VNbTaMoW）C 體系的高熵碳化物固溶體在較寬的溫度范圍（1 600～3 000 ℃）內熱力學穩定，而且預測的相組成和單相固溶體形成溫度與實驗結果非常吻合，有效地指導了（VNbTaMoW）C 超高溫高熵陶瓷的制備。受限于現有相圖數據庫，目前關于超高溫高熵陶瓷的相圖計算研究較少，尤其是對于復雜的硼化物超高溫高熵陶瓷體系的相圖計算更是少之又少。

圖2 （VNbTaMoW）0.5Cx體系的溫度-碳摩爾分數雙自變量相圖［43］Fig.2 The dual independent phase diagram of temperature-carbon mole fraction of （VNbTaMoW）0.5Cx system［43］

2.2 結構預測

2.2.1 電子結構

材料的電子結構可以反映其成鍵特征、晶格畸變等信息，進而可以揭示其結構穩定性及機械性能的微觀作用機制［6］。廣西大學唐碧玉團隊［44］基于密度泛函理論計算了（Hf0.2Zr0.2Ta0.2Nb0.2Ti0.2）B2硼化物高熵陶瓷的電子態密度，如圖3所示。（Hf0.2Zr0.2Ta0.2Nb0.2Ti0.2）B2高熵陶瓷在費米能級處的電子態密度（DOS）大于0，表明其本質上是金屬的，同時費米能級位于偽間隙谷，說明其具有較高的結構穩定性。（Hf0.2Zr0.2Ta0.2Nb0.2Ti0.2）B2在費米能級附近的電子態密度主要由金屬的d 軌道電子和B 原子的p 軌道電子貢獻。費米能級附近的Hf-d、Nb-d、Ta-d、Ti-d 和Zr-d 電子雜化，說明其在金屬原子平面形成了更穩定的鍵合；從-10 eV 到費米能級（0 eV），B-p 與Hfd、Nb-d、Ta-d、Ti-d 和Zr-d 電子雜化，說明B-Hf、BNb、B-Ta、B-Ti和B-Zr原子間具有共價鍵特征；由于難熔金屬與B原子的電負性不同，難熔金屬與B原子之間的化學鍵也具有離子鍵特性。硼化物超高溫高熵陶瓷通常具有多種成鍵特征，其電子結構預測對于其結構穩定性、機械及熱物理性能預測具有重要意義。

圖3 （Hf0.2Zr0.2Ta0.2Nb0.2Ti0.2）B2的電子態密度［44］Fig.3 The electronic density of states of（Hf0.2Zr0.2Ta0.2Nb0.2Ti0.2）B2［44］

2.2.2 晶體結構

由于超高溫高熵陶瓷材料不同組元之間的差異，導致其晶體結構中存在著嚴重的晶格畸變，而超高溫高熵陶瓷材料的這種晶體結構特征能夠顯著地影響其結構穩定性、力學及熱物理性能［45］，因此準確預測超高溫高熵陶瓷的晶格結構特征對其性能預測具有重要意義。云南大學毛勇團隊［46］采用第一性原理計算了（TiZrNbTa）C碳化物高熵陶瓷材料的晶體結構，計算的平衡晶格常數（a=0.450 5 nm）和密度（ρ=8.37 g/cm3）與文獻報道的實驗結果吻合，證明了計算結果的合理性。該研究同時預測了壓力對（TiZrNbTa）C體系晶格常數、密度、晶格畸變的影響，如圖4所示，結果表明增加壓力，使（TiZrNbTa）C體系的晶格常數減小，密度增加，但對材料的局域晶格畸變和晶體穩定性幾乎沒有影響。因此，原子尺度的模擬計算方法能夠獲得超高溫高熵陶瓷材料的局域結構特征信息，可作為原子尺度實驗表征技術的補充［47］。

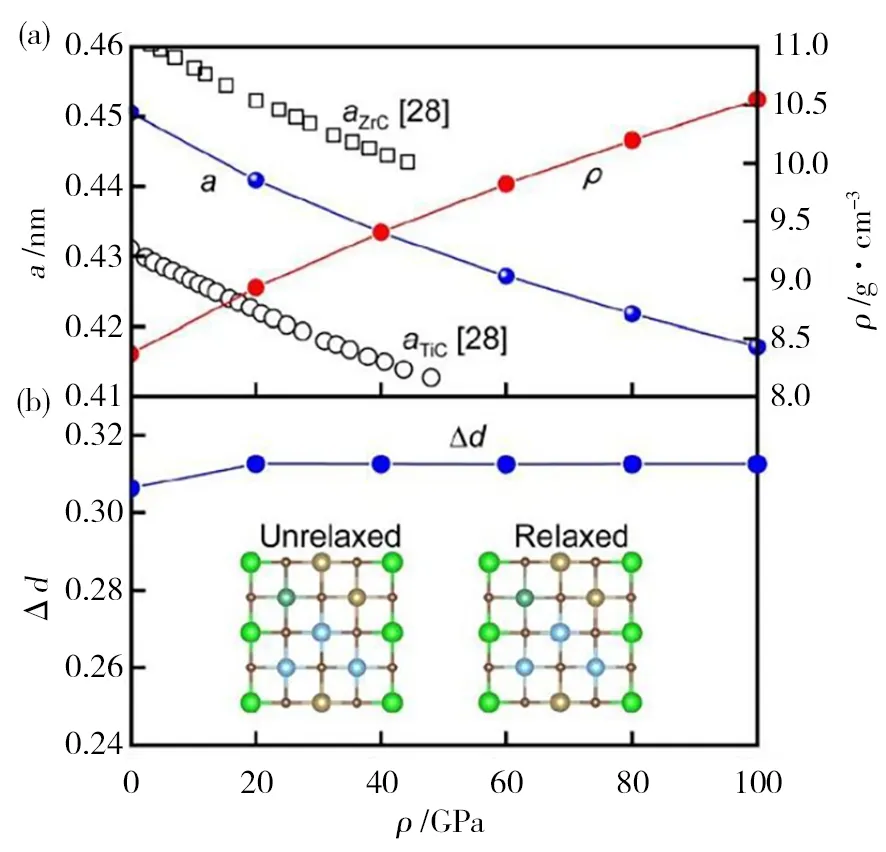
圖4 （TiZrNbTa）C體系的晶格參數、密度和局部晶格畸變隨壓力的變化規律［（b）中的插圖分別為未扭曲和扭曲的（100）原子層］［45］Fig.4 Lattice parameter，density and the variation law of local lattice distortion with pressure［the illustrations in （b） are undistorted and distorted （100） atomic layer，respectively］［45］

2.3 性能預測

2.3.1 彈性性能

彈性常數能夠提供材料的力學性能信息，通常是通過能量-應變方法獲得的。對于立方結構來說，有三個獨立的彈性常數（C11，C12和C44）［48］。一般來說，立方晶體的機械穩定性可以采用由彈性常數表示的通用穩定性標準來評估，即［49-52］：

表1為部分超高溫高熵陶瓷材料的彈性常數計算值。華南理工大學褚衍輝團隊［49］采用VASP軟件基于密度泛函理論的第一性原理計算了（Zr0.25Nb0.25Ti0.25V0.25）C高熵陶瓷的彈性常數C11，C12和C44分別為547.9、114.9和170.1 GPa，滿足穩定性標準，預測其具有機械穩定性，可有效地指導超高溫高熵陶瓷材料的體系設計。

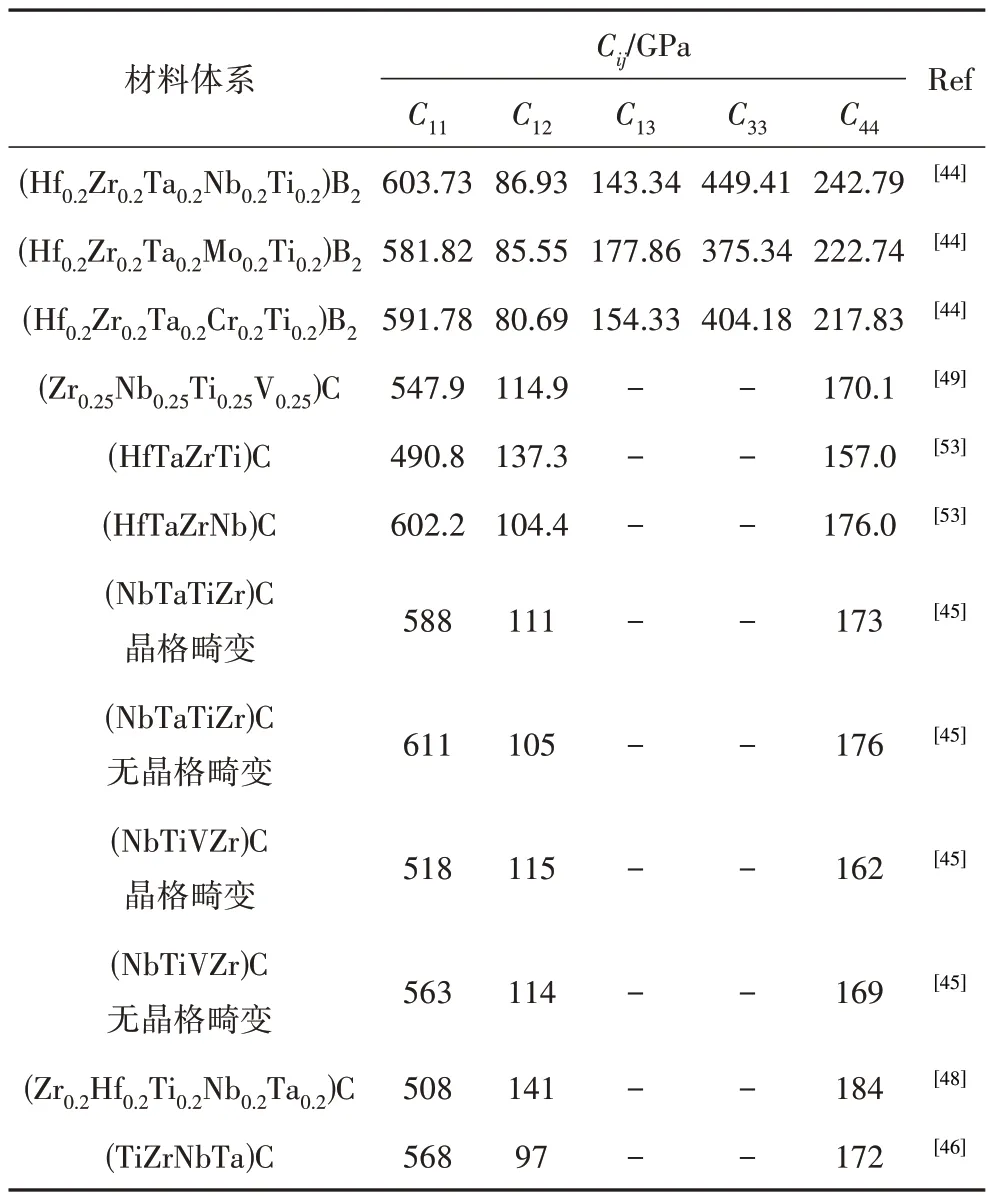
表1 部分超高溫高熵陶瓷材料的彈性常數Cij計算值Tab.1 Elastic constants Cij of some ultrahigh-temperature high entropy ceramics.

一旦計算出材料的彈性常數，通過Voigt-Reuss-Hill近似可預測材料的體積模量B、剪切模量G、Voigt剪切模量GV及Reuss剪切模量GR值，即［14，48，51-52，54］：

楊氏模量E和泊松比ν則可通過以下公式獲得［48，51-52，54］：

ν不僅可以預測材料的延展性，也可作為評價材料結合性能的指標。通常，彈性變形的ν在0.2～0.3。如果ν的值在0.1左右，說明材料是強共價晶體；如果ν≥0.25，說明材料是離子晶體。當ν＞0.26，一般認為材料具有延展性；反之則認為材料是脆性的［53］。

為便于比較，材料的硬度通常采用維氏硬度表示，理論維氏硬度（HV）可通過得到的體積模量B和剪切模量G進行估算，如下式所示［14，48，51，52，54］：

表2為部分碳化物超高溫高熵陶瓷的彈性模量、理論維氏硬度和泊松比計算值。廣西大學唐壁玉團隊［53］計算了（HfTaZrTi）C和（HfTaZrNb）C兩種碳化物高熵陶瓷的彈性性能，結果表明，（HfTaZrNb）C 的理論體積模量、剪切模量、楊氏模量和硬度均大于（HfTaZrTi）C，說明（HfTaZrNb）C 具有更高的抗體積變形、抗剪切應變的能力，且硬度更高。（HfTaZrNb）C和（HfTaZrTi）C 計算的ν分別為0.20 和0.23，說明這兩種碳化物高熵陶瓷的化學鍵既具有離子鍵又具有共價鍵特征，與（HfTaZrTi）C相比，（HfTaZrNb）C高熵陶瓷的泊松比更小，說明Nb-C鍵比Ti-C鍵共價性更強，材料更脆。第一性原理等多尺度模擬計算方法能夠預測超高溫高熵陶瓷材料的機械性能，可實現具備目標性能的超高溫高熵陶瓷體系的快速篩選。

超高溫高熵陶瓷材料的脆性通常較大，故而其脆韌行為對于其工程應用至關重要，可通過幾個經驗參數進行評估預測。PUGH［55］引入了一個經驗比B/G（Pugh比）來預測材料的脆韌行為，B/G＜1.75說明材料為脆性材料，反之為韌性材料。表3匯總了部分超高溫高熵陶瓷的B/G計算值，其中（HfTaZrTi）C的B/G值接近臨界閾值，說明其在一定條件下可能發生脆韌轉變［53］。此外，材料的脆性也可以通過柯西壓力標準［56］進一步確認。柯西壓力為負，表明材料為共價鍵結合，展現脆性；柯西壓力為正，則表明材料以金屬鍵為主，具有延展性。表3匯總了部分超高溫高熵陶瓷的柯西壓力計算值，均為負值，說明了絕大多數超高溫高熵陶瓷材料都是脆性的。香港城市大學的趙仕俊博士［45］采用VASP軟件分別計算了考慮和不考慮晶格畸變時，（NbTiVZr）C和（MoNbTaVW）C碳化物高熵陶瓷的彈性性能，如表2所示。該研究結果表明，對于（NbTiVZr）C 和（MoNbTaVW）C兩種碳化物高熵陶瓷均在未考慮晶格畸變的情況下，體積模量、剪切模量和楊氏模量更高，剛度更大；較高的泊松比值則說明晶格畸變使（NbTiVZr）C和（MoNbTaVW）C變得更軟更韌。與局域畸變增強高熵合金不同，晶格畸變可能會導致超高溫高熵陶瓷軟化。因此，可通過選擇合適的組成元素來調控超高溫高熵陶瓷材料的晶格畸變程度，進而實現超高溫高熵陶瓷性能的調控，該研究工作對超高溫高熵陶瓷材料的強韌一體化設計具有重要的指導意義。

表2 部分碳化物超高溫高熵陶瓷的彈性模量、理論維氏硬度和泊松比計算值Tab.2 Elastic modulus，theoretical Vickers hardness，Poisson’s ratio of some carbide ultrahigh-temperature high entropy ceramics

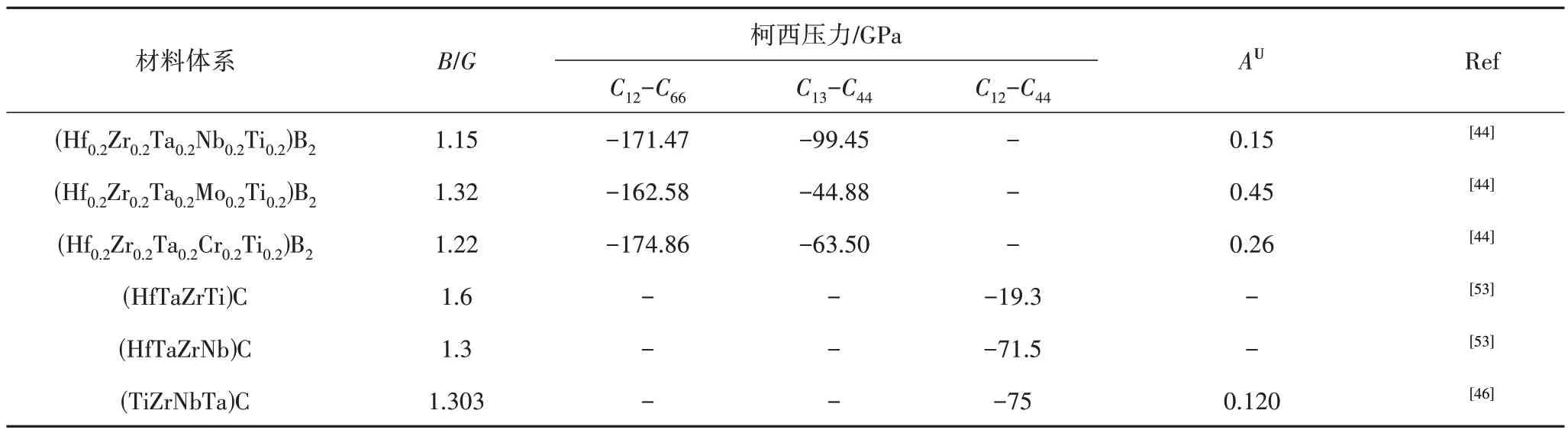
表3 部分超高溫高熵陶瓷的B/G、柯西壓力（Cauchy pressure）、AU計算值Tab.3 The B/G，Cauchy pressure，AU of some ultrahigh-temperature high entropy ceramics

材料的彈性各向異性對于工程應用也是至關重要的，可通過通用各向異性指數AU等經驗常數進行評估預測。AU=0表明材料是各向同性的，與0的偏差則代表了各向異性的程度［44］。表3中的三種硼化物超高溫高熵陶瓷材料的AU計算值結果表明，三種硼化物超高溫高熵陶瓷材料的彈性各向異性較小，且（Hf0.2Zr0.2Ta0.2Nb0.2Ti0.2）B2、（Hf0.2Zr0.2Ta0.2Cr0.2Ti0.2）B2、（Hf0.2Zr0.2Ta0.2Mo0.2Ti0.2）B2彈性各向異性程度逐漸增加［44］。該研究結果有利于進一步優化和設計具有優異機械性能的超高溫高熵陶瓷材料，加快其工程化應用進程。

目前碳化物超高溫陶瓷在與實際應用相關的溫度下的彈性性能的可用信息非常稀少，Link?ping 大學的SANGIOVANNI 等［57］人采用第一性原理分子動力學（AIMD）模擬了溫度對TiC、ZrC、HfC、VC、TaC，以及碳化物高熵陶瓷（TiZrHfTaW）C、（VNbTaMoW）C彈性性能的影響，計算結果如圖5所示。該研究結果表明，TaC 對高達1 200 K 的拉伸和剪切變形均表現出最高的彈性阻力，并優選出（VNbTaMoW）C 體系作為在室溫及高溫下具有優異韌性的候選材料。航天材料及工藝研究所周延春團隊［48，58］則運用深度學習勢函數預測了（Zr0.2Hf0.2Ti0.2Nb0.2Ta0.2）C 和（Ti0.2Zr0.2Hf0.2Nb0.2Ta0.2）B2超高溫高熵陶瓷彈性性能隨溫度的變化規律，研究結果表明兩種超高溫高熵陶瓷的彈性常數及模量隨著溫度的升高呈線性降低趨勢，且預測結果與文獻報道的實驗結果吻合良好。但由于硼化物具有多種成鍵特征（包括B-B 共價鍵、M-B 離子-共價鍵、M-M 金屬鍵），所以與碳化物相比，深度學習勢函數對硼化物性能的預測精度相對較低。綜上所述，超高溫高熵陶瓷材料的機械性能，甚至許多傳統方法難以獲得的或需耗費大量時間和經濟成本的超高溫力學等材料性能，均可借助第一性原理、分子動力學、機器學習等多尺度模擬計算方法進行預測分析，有效提高超高溫高熵陶瓷材料的研發效率。

2.3.2 熱學性質

德拜溫度θD作為固體材料的一個基本參數，與材料的熔點、比熱容、熱導率等多個物理量密切相關，還可以表征原子間的成鍵特征，反映固體的熱力學性質［48，59］。德拜溫度可通過下式計算得出［60］：

式中，kB為玻爾茲曼常數，vm為平均聲速，ρ為密度，NA為阿伏伽德羅常數，M為摩爾質量，h為普朗克常數，n為原胞中的原子數。由密度、體積模量和剪切模量，可以獲得橫向聲速vt、縱向聲速vl和平均聲速vm［48，59］：

進而，根據Slack 方程可以計算與溫度相關的熱導率［61］：

表4匯總了部分超高溫高熵陶瓷的密度ρ、vs、vl、vm和θD的計算值。云南大學毛勇［46］等計算了不同壓力條件下（TiZrNbTa）C 碳化物高熵陶瓷的vs、vl、vm和θD，研究結果表明（TiZrNbTa）C 的平均聲速和德拜溫度隨著壓力的增加而增加，德拜溫度越高，原子間相互作用力越強，熱導率也越高。因此，增加壓力可能有利于增加超高溫高熵陶瓷的熱導率和化學鍵合。該研究工作為深入了解高壓下超高溫高熵陶瓷材料的性能提供了一種新思路，有助于超高溫高熵陶瓷材料的進一步研究和應用。

表4 部分超高溫高熵陶瓷的密度ρ、vs、vl、vm和θD的計算值Tab.4 The density，vs，vl，vm and θD of some ultrahigh-temperature high entropy ceramics

航天材料及工藝研究所周延春團隊［48］采用深度學習勢函數方法計算了（Zr0.2Hf0.2Ti0.2Nb0.2Ta0.2）C高熵陶瓷在0～2 400 ℃內的晶格常數、熱膨脹系數及聲子熱導率，如圖6所示。當溫度從0增加到2 400 ℃，晶格常數從4.570 7×10-10m增加到4.672 7×10-10m，熱膨脹系數從7.85×10-6K-1增加到10.58×10-6K-1，聲子熱導率從2.02 W/（m·K）減少到0.95 W/（m·K）。該研究預測（Zr0.2Hf0.2Ti0.2Nb0.2Ta0.2）C高熵陶瓷的室溫特性與實驗測量結果吻合，表明深度學習勢函數方法具有較高的準確性，而且為傳統方法難以測量的超高溫熱學性能提供了一種新的預測分析方法。

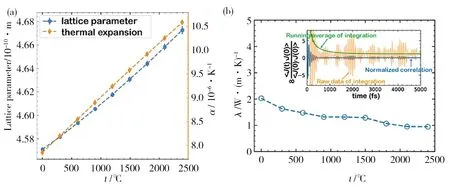
圖6 （Zr0.2Hf0.2Ti0.2Nb0.2Ta0.2）C高熵陶瓷晶格常數和熱膨脹系數與熱導率隨溫度的變化［48］Fig.6 The variation of lattice parameters and thermal expansion coefficients and phonon thermal conductivity of （Zr0.2Hf0.2Ti0.2Nb0.2Ta0.2）C with temperature［48］

3 結語

面對復雜成分空間及服役環境的超高溫高熵陶瓷材料，采用多尺度模擬計算方法能夠大幅度提高材料的研發與應用效率，縮短材料研發周期。但目前面向超高溫高熵陶瓷材料的計算平臺計算能力不足；關于超高溫高熵陶瓷材料無序結構建模、服役性能預測等計算軟件和核心算法匱乏；實驗數據封閉、離散且缺乏規范性，導致材料計算效果差。未來關于超高溫高熵陶瓷的材料計算研究應主要集中在以下幾個方面：

（1）開展超高溫高熵陶瓷材料服役性能預測研究，建立以需求為導向的超高溫高熵陶瓷材料設計方法；

（2）開發具有協同設計效應、適用于超高溫高熵陶瓷的高置信多尺度模擬算法，并將核心算法組件化，實現標準化的超高溫高熵陶瓷計算平臺構架設計；

（3）建立超高溫高熵陶瓷信息數據庫，結合人工智能技術和超高溫高熵陶瓷領域知識，建立更高效的機器學習網絡，實現智能數據分析和擴展。