陳明菊

一、 引言

素質教育背景下，數學核心素養逐漸成為教育教學中重點關注的內容，但是結合實際的教育教學會發現，這一時期的數學知識極具深度，學生在知識探究中極易產生消極心理，對學生后續的發展有著阻礙作用。為解決這一教育問題，教師在實際的教育教學中可引入轉化與化歸思想，在凸顯學生課堂地位的同時實現學生數學素養提升的目標，對學生發展產生的助推作用顯著。但在實際的教育中，受到多種因素的影響，轉化與化歸思想的應用存在較多問題，制約了學生數學素養的提升，教育效用得不到發揮和體現。針對此，關注和重視教育模式革新是很有必要的，這也是當前高中數學教學中重點研究的內容。

二、 轉化與化歸思想在高中數學教學中的應用背景分析

近年來，在社會持續發展和進步的背景下，各行各業對高素質人才的要求和標準顯著提升，傳統的教育教學模式存在顯著的局限性，難以適應當前社會發展需要。為更好地滿足當前社會發展的具體要求，需要關注教育革新，在課堂教學中注重學生地位，堅持教育教學始終圍繞學生學科素養的提升，由此確保學生發展進步，滿足當前社會發展要求。具體來說，傳統的教育教學一味關注學生知識的掌握，并沒有注重學生學習意識以及能力的培養，并且課堂教學中沒有關注學生的課堂地位，導致學生在其中難以積極融入，整體教學質量始終得不到有效提升。此外，在教育和教學中由教師組織和開展的課堂教學大多局限于數學知識和解決問題的教學，而不關注和重視對學生數學思想和能力的培養和發展，造成學生的數學素養得不到提升，無形中也會對學生發展產生阻礙現象。而轉化與化歸思想是一種以學生為中心的教育思想，將其應用在高中數學的教育中不但能夠實現學生學習成效提升的目標，還能夠促使學生在實際的學習中發展自身的數學思維和能力，同時還能夠培養學生的質疑能力和探究思考能力等，在滿足素質教育標準的同時強化學生的綜合素養。基于此，在高中數學的教學中應用轉化與化歸思想是教師當前重點關注的內容，也是提升高中數學教學有效性的關鍵舉措，教育實效顯著。

三、 轉化與化歸思想在高中數學教學中的應用困境分析

(一)應用意識不足

綜合實際的教育教學發現，轉化與化歸思想在高中數學的教育中有著非常積極的作用，產生的教育實效顯著。所謂的轉化與化歸思想是指在學習探究中運用分析、觀察、類比、聯想等方式對未知的問題、難以解決的問題進行轉化，然后將其歸結到自己已知的知識范圍中，然后再進行解決。在此過程中，既能夠消除學生的懼學心理，還能夠強化學生的學習有效性，產生的積極作用顯著。但是結合實際的教育教學發現，在高中數學課堂的教學中部分學生在解決數學問題中沒有具體的思路，或者會受到自身主觀因素的影響并沒有積極探究，或者在進行轉化與化歸中不能將具有難度的知識轉化為已知以及熟悉的知識內容，整體實效低下，并不能滿足實際的學習需要。或者部分學生在問題的探究中出現思維局限現象，僅是一味套用數學公式以及定理等，沒有對問題中的已知和未知條件進行分析，缺乏轉化與化歸意識，這樣也會造成學生的解題效率低下，對后續的學習與發展也會產生制約。

(二)學習探究把握不準確

所謂的轉化與化歸思想在一定程度上是指將具有難度的知識轉化為學生熟悉的知識，這樣能夠保障學生理解并掌握其中的知識內涵，對實現其學習能力以及問題分析、解決能力有著積極的作用。從轉化的類型來說，在實現問題的轉化與化歸中能夠立足學生發展特征和需要將抽象性較強的問題轉化為較為具體的問題，同時也能夠使復雜難懂的知識轉化為簡單易懂的知識內涵，對強化學生的探究有效性具有積極的作用，即在這一思想的作用下能夠降低探究的難度，促使學生在其中積極體會和探究。但是結合實際的探究能夠發現，當學生在學習新的知識或者抽象性較強的函數知識時會產生各種問題，難以進行類比或者轉化分析，整體的學習探究實效低下，不能滿足實際的學習發展需要。或者出現討論情況較多的現象時，不能利用特殊值、特殊點等對相應的估值進行處理；或者在遇到難度較大的問題時不能進行建模，轉化實效不高，也會造成學生積極性降低。這些問題的產生與學生對轉化與化歸類型把握不準確有關，在實際的探究中出現各種各樣的問題，致使學生的探究實效降低。

(三)探究方法掌握不扎實

結合實際的學習與探究發現，具體的學習探究方法包括換元法、屬性轉化法、等價轉化法、補集轉化法等，對不同的數學問題應采用不同的探究方法，這樣才能夠確保最終的學習有效性。但是結合實際的探究會發現，學生對這一學習探究的具體方法掌握不足，在問題解答中出現各種各樣的問題，影響了最終教育教學的有效性。例如，在進行正面求值困難時可以從反面進行思考和解答，但是由于學生對知識的理解不足，在解答中會出現問題，不能從反方向進行思考，問題解答實效降低。或者部分題目中出現了不少于、不大于或者至少等關鍵詞時，若不能從反面進行分析解答就可以從補集轉化的方式進行探究，也能夠保障探究實效，但是學生對這一方法掌握不足，導致相應的應對實效低下。三角函數、一般函數形式、零點個數等是高中數學中的重難點，學生可利用屬性轉化的方式進行解答，但在實際的教育教學中，學生對這一學習方法掌握不足，導致在問題解答中不知道如何入手，不僅會影響最終的解答有效性，并且還會造成學生出現學習盲目現象，對學生未來的發展和進步也會產生阻礙。

四、 轉化與化歸思想在高中數學中培養原則分析

結合上述觀點的分析發現，轉化與化歸思想在高中數學中的應用能夠實現教育教學強化，對學生數學素養的提升有著積極的作用。但是受到多方面因素的影響，在這一教學思想的應用中存在較多的問題，學生在其中難以積極融入和體會，致使最終的教育有效性降低，而且學生也無法從中獲得和體會相應的知識體驗。針對此，為保障學生能夠在其中獲得和感悟更多的知識體驗，需要教師關注對轉化與化歸思想的應用培養原則分析，立足學生發展特征和具體需要實現教育優化，由此強化學生的數學學習力、發展力。

(一)隱性轉顯性

這一教學思想在數學課堂教學中有著顯著的課堂地位，其并不是簡單的數學公式，而是充斥在整個數學知識體系中，貫穿數學教學的整個過程。因此，在實際的教育教學中需要教師關注這一教學思想深化，轉化與化歸思想大多依托在具體的數學知識中，二者形成相互依存的關系，而在實際的知識探究中并沒有明確告知學生如何使用這一教學思想解決實際的教育問題。為保障學生能夠從中獲得更多的知識體驗，需要教師在實際的教育教學中堅持“隱性轉顯性”原則，充分體現這一教學思想的效用與價值，使得學生能夠認識并正確運用這一思想實現學習探究深化，將復雜難懂的知識轉變為具體、直觀且簡單易懂的知識，由此強化學生的學習有效性。

(二)系統性

具體來說，數學知識與化歸思想處于有機的統一體中，注重二者的聯合能夠為轉化與化歸思想的滲透提供相應的助益，學生對數學知識的探究學習也能夠實現全面、深度的目標，使得學生在此基礎上夯實數學思維，進而解決學習探究中存在的諸多問題。也就是說，在實際的轉化與化歸思想滲透中應關注這一教育思想與學生學習探究實效間的關系，實現思想滲透，豐富知識探究內涵，促使學生能夠在實際的學習探究中獲得不一樣的學習體驗，對學生未來的發展和進步產生的積極作用顯著。

(三)參與性

所謂的參與性是指在實際的思想滲透中應關注學生的學習地位，不能出現教師主導性過強而學生參與度低下的現象，這樣不但會造成這一教學思想實效低下，而且極易產生消極的學習心理，影響數學課堂教學有效性。因此，在實際的思想滲透中教師需要注重學生課堂地位，通過引導和啟發學生在主動探究中了解并明確什么是轉化、如何轉化，這樣才能夠促使學生在主動探究中明確學習思想和具體觀念，掌握其中的學習與探究方法。總的來說，在教育教學中注重教學思想的融入能夠實現課堂教學優化，對實現學生數學素養的建設提升有著非常積極的作用，為凸顯這一教學模式的有效性，在實際的教育教學中需要關注學生的課堂地位，促使學生在實際的課堂中主動學習并探究，這樣既能夠實現學生學習力強化的目標，還能夠促使學生在主動參與中獲得更多的知識體驗，對學生未來的發展和進步能夠起到積極的作用，產生的教育實效顯著。

(四)螺旋上升性

具體來說，在培養學生轉化與化歸思想的過程中需要教師注意，整個思想的滲透教育不能像數學公式、數學概念等進行一步到位的教學，需要長時間的引導和促進，確保學生在其中獲得和感悟不同的知識體驗，對學生數學綜合素養的提升產生的積極作用顯著。即在實際的教學中應對不同階段的學生實施不同程度的教學和培養，使得學生能夠在學習發展中實現“從一般到特殊、從簡單到復雜、從直觀到抽象”螺旋式上升中培育和發展學生的轉化與化歸思想的目標，對學生未來的發展和進步有著非常積極的作用。

五、 高中數學中轉化與化歸思想的應用分析

(一)關注學生課堂地位，轉變教學引導模式

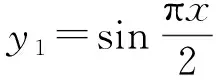
(二)注重課堂教學優化，引導學生積極探究

現階段的教育教學更加關注和重視學生綜合素養的樹立，因此教師在教育教學中應轉變教育思想，不僅要關注學生的課堂地位，還需要關注課堂教學模式革新，積極引入轉化與化歸思想，促使學生在其中體會和感悟相應的知識內涵，從而實現學生學習素養強化的目標。結合實際的教育教學發現，函數與方程是高中數學中的教學重點也是難點，部分學生在學習探究中會產生各種各樣的問題，不但造成消極心理加重，而且對學生數學綜合素養的提升也會產生阻礙作用。為更好地解決這一教育問題，在實際的教育教學中教師可以應用這一教學思想，促使學生在其中積極融入，更好地體會其中的知識內涵。就以人教A版必修一第三章函數的應用中的《函數與方程》為例，其中的函數是方程與不等式間的“中介”，它們之間既有區別也有非常密切的聯系，因此有關學者提出函數、方程與不等式是“一胞三兄弟”的關系，所以在實際的學習探究中可以結合三者間的關系進行學習探究，這樣既能夠加深學生對所學知識的理解，還能夠在探究中體會數學學習的連續性、結構性、系統性，實現學生數學思維以及學習能力的建設強化。如在本章知識的探究中可以對三者間的關系以及探究重點進行轉化，都能夠減輕探究的難度。

(1)討論f(x)的單調性；

解析：(1)略

(2)通過分析已知條件能夠發現f(x)存在兩個極值點當且僅當a>2。

∵f(x)的兩個極值點x1、x2滿足x2-ax+1=0，

∴x1x2=1，假設01。

通過分析(1)能夠發現，g(x)在(1，+∞)上為單調遞減，

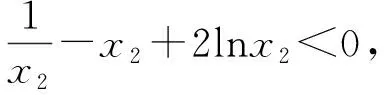
(三)立足課堂教學優化，實現教學質量提升

高中時期的數學知識有著顯著的學習深度和探究難度，部分學生在數學學習中會產生諸多的消極心理。為保障學生能夠在其中獲得和感悟更多的知識體驗，現階段的教育教學中教師開始關注和重視學生的課堂地位，并結合學生實際需要和特征進行教育優化，促使學生能夠在實際的學習探究中獲得更多的知識體驗。其中轉化與化歸思想在凸顯學生課堂地位的同時發散學生的學習思維，使得學生能夠在其中獲得和感悟更多的知識體驗，有助于強化學生的知識獲得感和體驗感。例如，在進行人教A版選修2-1第二章圓錐曲線與方程中的“拋物線”時，教師在實際的課堂教學中可以積極采用轉化與化歸教育思想，引導學生進行探究體會，從中掌握相應的知識內涵。結合實際的探究學習能夠發現，由于本課時的知識具有一定的探究難度，學生在實際的學習探究中極易產生消極心理，就以下述案例為例：

已知三條拋物線：y=x2+4ax-4a+3，y=x2+(a-1)x+a2，y=x2+2ax-2az中至少有一條與x軸相交，求實數a的取值范圍。部分學生在解答過程中多會從正面進行，而正面討論探究需要進行分類討論求解，整個解題過程較為煩瑣，但是通過轉化與化歸的思想進行引導，能夠從反面進行探究，不僅效率快，而且正確率較高。具體分析如下：

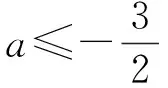
從題目反面“三條拋物線都不與x軸相交”入手進行分析，能夠獲得a的取值范圍，然后再求其補集，這樣就能夠顯著降低問題的探究難度。由此發現，轉化與化歸思想能夠將復雜的問題轉變為簡單的探究內容，從不同角度進行探究，有助于實現學生數學思維的發散和數學能力的發展。

(四)注重知識內涵分析，凸顯轉化教學效用

除卻上述提到的函數以及拋物線的學習探究外，概率相關的知識中也能夠利用這一教育思想實現教育優化，對學生數學思維的培育也能夠起到積極的作用。例如，在學習人教A版必修三中第三章的概率時，其中主要學習了隨機事件的概率、古典概型和幾何概型，其中的內容對學生的理性思維和探究能力有著一定的要求，為保障學生能夠更好地理解，教師可以改變從“正面進攻”的教育模式，引導學生從反面利用補集思想進行探究。比如，在套圈游戲中，小小套中目標的概率為0.9，連續套圈4次且她每次套圈是否擊中目標是相互獨立的，問：她至少套中目標一次的概率是多少？

解析：在這一事件的分析中應對可能會出現的情況進行分析，如她套中的目標一次的情況包括1次、2次、3次、4次，一共會出現這四種情況，所以在解析中我們可以將其轉化為其對立事件——“一次都未中”進行求解。通過這一分析，學生能夠在學習探究中學會轉變思維，相應的學習有效性得以顯著提升。

六、 結語

綜上所述，在高中數學的課堂教學中注重轉化與化歸思想的應用，能夠實現學生數學思維發散和數學能力發展的目標，對學生數學素養的提升有著非常積極的作用。因此，在實際的教育教學中應關注和重視學生發展特征分析，立足學生角度注重對這一教育思想的應用，由此為學生構建更好的學習成長氛圍，助推學生更好地發展進步。