載荷作用下的天然氣管道斜接管強度評估

張利杰 賀新紅

（浙江省電力建設有限公司，浙江寧波 315000）

0 引言

天然氣是現今使用較為廣泛的清潔能源之一，在中國能源結構調整中占據著關鍵位置，也是改善生態環境的主要途徑之一。調查研究數據顯示，截至2021年底，中國天然氣消費量達到了3 726億m3，在能源消費中占比較大，并呈現出逐年遞增的趨勢。由此可見，天然氣發展情況的好壞直接關系著中國社會經濟發展狀況。管道是天然氣運輸的關鍵載體，目前，中國已經完成全國管網的建設，主要包含主干線、聯絡線、省際線、配氣線等。隨著經濟水平的不斷提升，天然氣供應需求量急劇增加，對天然氣管道建設提出了更高的要求，管道能否穩定、安全運行成為影響天然氣供應的關鍵所在[1]。

近年來，天然氣管道斜接管安全事故頻發，給相關部門留下了慘痛的教訓。以某省管道爆炸事故為例，該事故造成了多人受傷與死亡，經濟損失高達600萬元，并致使事故區域天然氣供應停滯約1個月時間，這表明中國在天然氣管道監控方面還存在著很多的不足。對天然氣管道事故進行統計分析，發現由斜接管強度不足引發的事故在頻率上占比第一，而且在提出與實施多條監管措施的背景下，此類事故發生頻率依舊居高不下，故提出了載荷作用下天然氣管道斜接管強度評估方法的研究。

1 天然氣管道斜接管強度評估方法研究

1.1 斜接管有限元模型構建

為提升斜接管強度評估的精度，首要任務就是構建斜接管有限元模型，并對其進行有限元分析，為后續極限載荷的計算奠定堅實的基礎[2]。

斜接管有限元分析結果與其單元形式之間存在著緊密的聯系，單元形式選取是否正確會影響強度評估結果的精度，由此可見，正確選取單元形式是有限元分析的基礎與前提。單元形式主要包括面、線、板殼和三維實體[3]，在斜接管有限元模型構建過程中，通過每種單元形式優劣勢的分析與探究，結合斜接管的實際情況，選取三維實體單元形式作為有限元模型構建單元，其能夠清晰地模擬斜接管完整應力分布情況，并且該單元形式適應性較強，能與多種形狀相協調，更加能夠體現斜接管與管道連接位置的實際情況，為有限元分析提供支撐。

斜接管有限元模型構建過程中，網格劃分也是一個至關重要的環節，網格質量與數量是影響后續分析與計算的關鍵因素。為了提升構建模型的精密性，將其分割為三個部分，分別為管道、斜接管及二者連接區域。需要注意的是，對管道與斜接管連接區域的網格劃分應該更加精細。雖然精細網格劃分會延長有限元模型構建的時間，但卻能夠獲得精度較高的分析結果，對研究來說，利大于弊，故應最大限度地精細劃分斜接管有限元模型網格[4]。

為簡化研究過程，利用斜接管結構的對稱性，依據上述選取的單元形式、確定的網格劃分規則，截取斜接管結構的1/2進行有限元建模，具體如圖1所示。

圖1中，L與D表示管道的長度與內徑；l與d表示斜接管的長度與內徑；θ表示斜接管與管道的夾角。

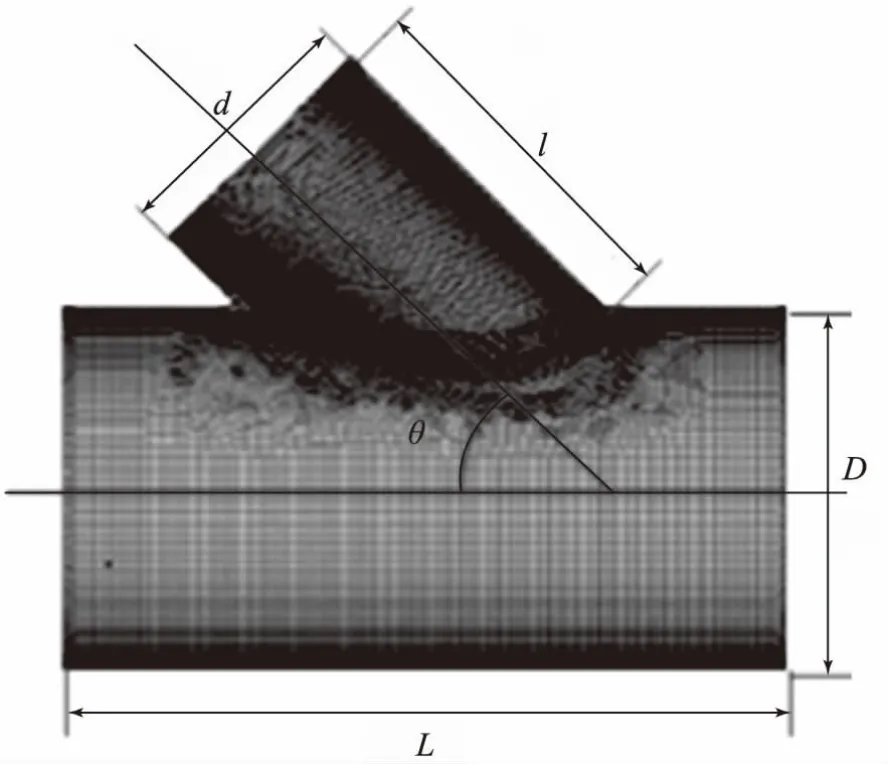
圖1 斜接管有限元模型示意圖

以上述構建的斜接管有限元模型為基礎，對其載荷與邊界條件進行深入探究，為后續極限載荷的計算提供支撐。在斜接管實際應用過程中，其載荷來自多個方面的共同作用，但以內壓為主[5]。常規情況下，隨著內壓的不斷加大，斜接管與管道連接區域受到的壓力也會增加，從而產生變形現象，若變形超過一定的閾值，則會導致管道破裂的事故。

斜接管載荷計算公式為：

由于構建模型具有對稱性，將斜接管斷面全部節點進行旋轉變換，并對其進行位移約束，即可獲得斜接管邊界信息，為后續研究的進行提供便利。

上述過程完成了斜接管有限元模型構建，奠定了研究進行的基礎與前提。

1.2 斜接管極限載荷計算

以上述構建的斜接管有限元模型為基礎，衡量斜接管應力集中系數，以此確定斜接管的極限載荷，為最終斜接管強度評估的實現提供依據。

應力集中系數反映的是在載荷作用下斜接管局部范圍內應力明顯增大的程度，計算公式為：

式中：β為應力集中系數；υθ為實時應力值；αθ′為最大基本應力；P為極限載荷；k為斜接管管道材料厚度。

在斜接管應用過程中，隨著載荷數值的不斷增加，斜接管與管道連接區域最先開始屈服，應力由此向外擴展。但是，管道具有一定的彈性，當載荷數值在閾值以下時，斜接管處于彈性階段，應力分布呈現一定的規律性，并不會對管道安全產生較大的影響[6]。當載荷數值超過閾值時，斜接管處于塑性階段，應力分布呈現出無規律性，管道開始出現形變。形變若是過大，管道就會發生破裂，導致天然氣泄漏，如在此時遇到明火，就會發生爆炸事故。需要注意的是，應力變化情況與斜接管實際結構沒有關系，但其與斜接管、管道的夾角θ存在著較為密切的關系。常規情況下，應力值υθ隨著夾角θ的增大而減小，兩者呈現明顯的負相關關系。因此，在管道建設過程中，應該盡可能采用夾角大于30°的斜接管結構。

與此同時，隨著載荷數值的增加，斜接管變形程度加大。獲取斜接管應力分布數值，將其代入公式（2），經過方程式求解，即可獲得斜接管極限載荷P，為后續研究的進行提供助力。

1.3 斜接管內腐蝕預測

隨著應用時間的增加，斜接管內部會產生腐蝕現象，這也是影響其強度的關鍵因素，故此節對斜接管內部腐蝕情況進行預測，為最終強度評估的實現提供依據[7]。

根據已有文獻研究可知，造成管道內部腐蝕現象的主要參數為溫降、壓降與平均腐蝕速率。其中，溫降計算公式為：

式中：T為溫降參數數值；T0為管道內部初始溫度；TQ為斜接管內部實時溫度；M為輔助參數；CP為斜接管應力變化因子；P0為斜接管初始應力數值。

壓降參數無法直接測量獲得，需要通過下述方程計算而得：

式中：Z為壓降參數數值；R為斜接管內部半徑數值；g為重力加速度；χ為輔助運算因子，取值范圍為0～1。

平均腐蝕速率需要依據實際天然氣運輸情況進行預測，表達式為：

式中：Vτ為平均腐蝕速率數值；p與q為隨機整數；F（v）為天然氣運輸過程中管道的損失系數；G（t）為腐蝕時間系數；Vc為標準腐蝕速率。

依據公式（3）（4）（5）計算結果，預測斜接管內腐蝕情況，為了方便研究，將其轉換為斜接管內壁面損失，表達式為：

式中：ζ為斜接管內壁面損失；σ2為斜接管內腐蝕程度參量。

一般情況下，壁面損失越大，則斜接管厚度越薄，其強度也就越差。

上述過程完成了斜接管內部腐蝕情況的預測，為研究目標的實現提供了支撐。

1.4 斜接管強度評估實現

以上述獲得的斜接管內壁面損失數值為基礎，制定斜接管強度評估程序與規則，獲取精準的斜接管強度結果，為天然氣管道的安全使用提供保障。

斜接管強度評估是天然氣管道運行過程中的關鍵環節之一，是管道檢查與維修的主要依據。依據斜接管實際作業情況，制定強度評估程序，具體如圖2所示。

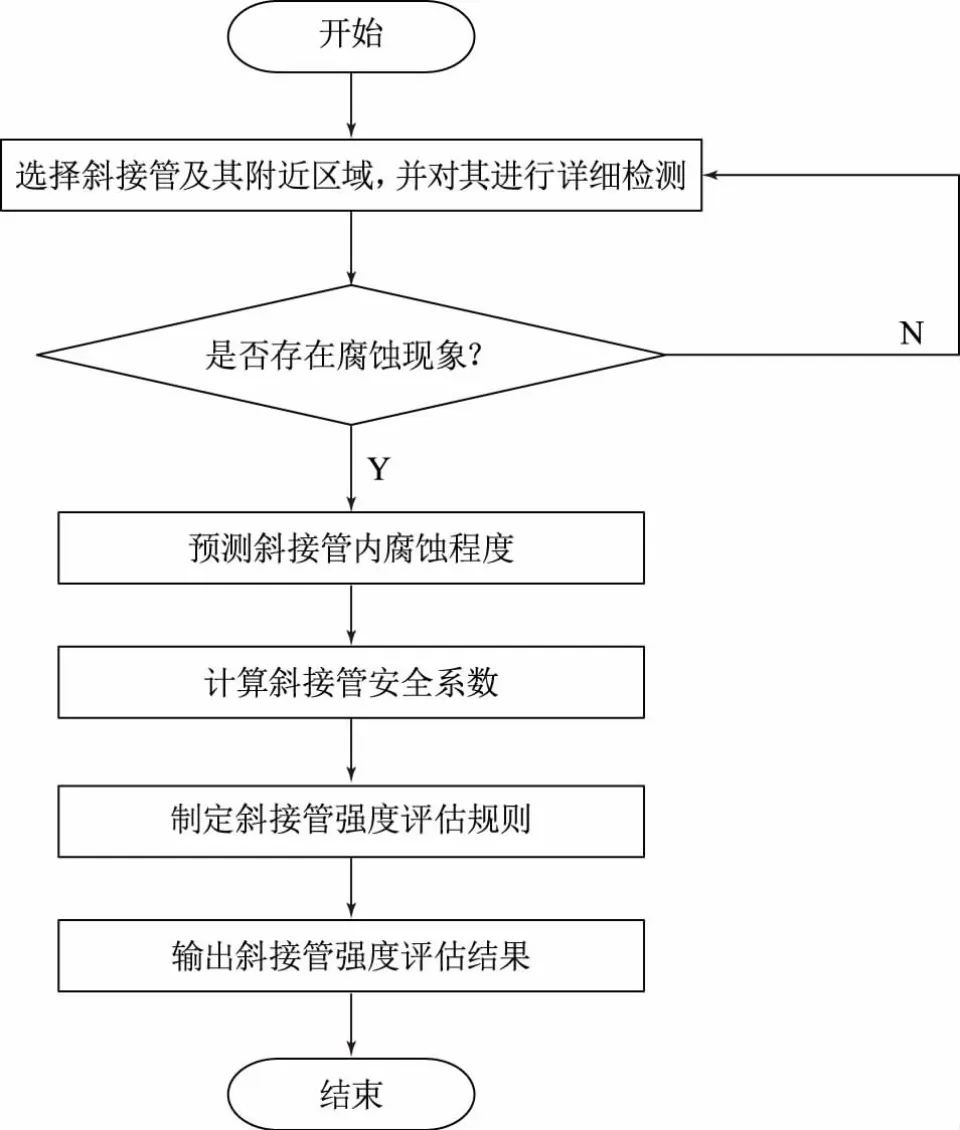
圖2 斜接管強度評估程序圖

如圖2程序所示，斜接管安全系數的計算是強度評估的主要數據依據，計算公式為：

式中：Г為斜接管安全系數；ξm為腐蝕預測的分項安全系數；t為時間；η為固定的最小拉伸強度；ξd為腐蝕深度的分項安全系數；Q為長度校正系數。

以公式（7）計算結果為基礎，制定強度評估規則，具體如下：

（1）當Г處于[0.0，0.3]范圍內時，認定斜接管強度較差；

（2）當Г處于[0.4，0.5]范圍內時，認定斜接管強度一般；

（3）當Г處于[0.6，0.8]范圍內時，認定斜接管強度尚可；

（4）當Г處于[0.9，1.0]范圍內時，認定斜接管強度較好。

依據上述制定的評估規則，即可實現天然氣管道斜接管強度的精準評估，為天然氣穩定傳輸提供助力。

2 實驗與結果分析

2.1 實驗對象概況

選取某段天然氣管道作為實驗對象，其長度約為8 700 km，內部包含25個斜接管，并且斜接管應用的時間長度存在著明顯的差異。管道采用的是國產X80管線鋼，內部包含Mo、Cr、Nb、Ni、P、C等元素，具有較好的耐腐蝕性能，可以保障天然氣管道安全、經濟、高效運行。

隨著天然氣供給需求的增加，實驗對象——天然氣管道面臨著較大的挑戰，對斜接管性能的要求更高，因此需要對斜接管強度進行實時監測，符合所提方法應用性能的測試需求。

2.2 實驗結果分析

以上述選取的實驗對象為依據，進行天然氣管道斜接管強度評估實驗。為凸顯本文所提方法的應用性能，選取含等壁厚體積型缺陷油氣管道的剩余強度評價[8]與艦船內腐蝕海水管路剩余強度預測模型及試驗驗證[9]作為對比方法1與2，并選取斜接管極限載荷計算誤差與斜接管強度評估結果作為評價指標。

通過實驗獲得斜接管極限載荷計算誤差數據如圖3所示。

圖3 斜接管極限載荷計算誤差數據圖

如圖3數據所示，相較于兩種對比方法，應用本文方法獲得的斜接管極限載荷計算誤差數值更小，最小值為0.2%。

通過實驗獲得斜接管強度評估結果如表1所示。

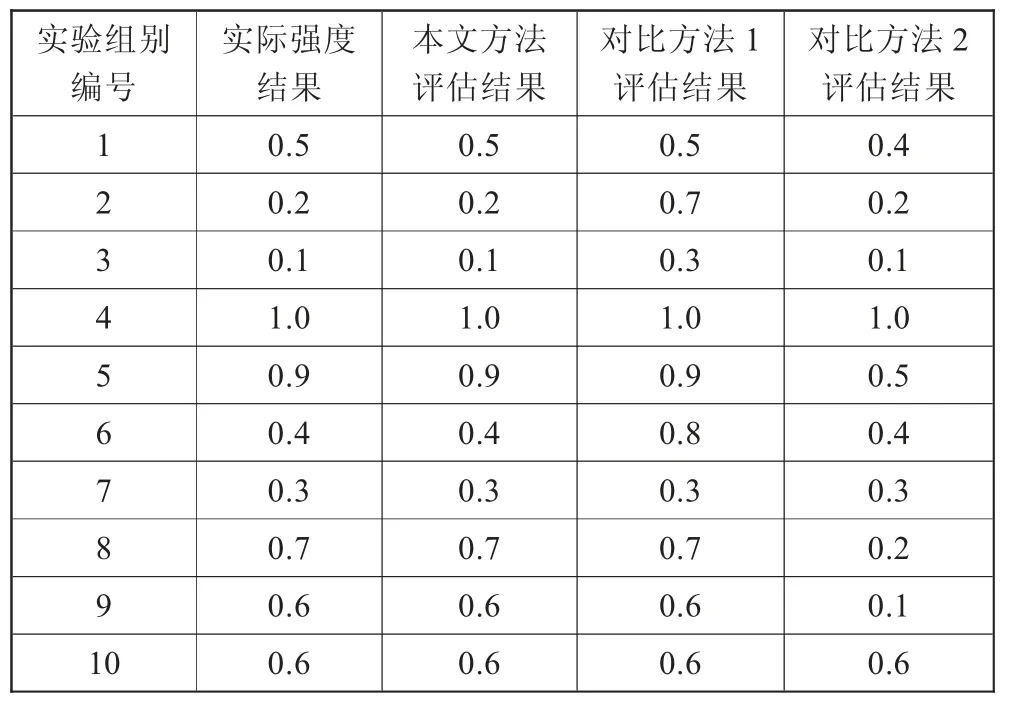
表1 斜接管強度評估結果表

如表1內容所示，應用本文方法獲得的斜接管強度評估結果與實際情況保持一致，而對比方法1與2獲得的斜接管強度評估結果與實際情況存在較大偏差，說明應用本文方法獲得的斜接管強度評估精度較高。

上述實驗數據顯示，與兩種對比方法相比較，應用本文方法獲得的斜接管極限載荷計算誤差較小，斜接管強度評估結果與實際情況趨于一致，充分證實了本文方法應用性能更好。

3 結語

天然氣是現今社會應用極為廣泛的清潔能源之一，其主要通過管道進行運輸，管道是否安全直接關系天然氣企業的發展，故提出載荷作用下的天然氣管道斜接管強度評估方法研究。本文所提方法有效降低了斜接管極限載荷計算誤差，提升了斜接管強度評估精度，為天然氣管道管控提供了更加精準的數據支撐，也為相關研究提供了一定的借鑒與參考。