基于改進拉普拉斯中心性的高速路網狀態識別方法

薛相全，龐明寶

(河北工業大學土木與交通學院，天津 300401)

路網交通狀態反映了路網運行狀態，其有效識別是提升道路運行效率的關鍵所在，且網絡層面的狀態識別方法一直是研究熱點[1-2]，但高速公路網絡狀態識別研究較少。Han等[3]、Cassidy等[4]基于宏觀基本圖(macroscopic fundamental diagram, MFD)，利用高速路網各子路段交通參數加權和來描述宏觀的交通參數關系，以圖轉折點為依據來識別狀態，但高速公路交通流時空分布不均使路網內車輛密度并不均勻，因而適用于路段狀態均勻的MFD可行性有待進一步研究[4]。

高速路網由交通流特性各異的純主線路段、含出入口匝道路段、含立交橋路段等組成，各類型路段(節點)對路網運行狀態影響存在時空差異性[5-6]，需加以區分，如丁恒等[7]以單位長度通行能力區分純主線路段、含出入口匝道路段，但區分方式過于簡單、 主觀人為因素過多，無法有效區分節點的影響程度。拉普拉斯中心性法[8-9]因為客觀直接、精準有效，常用于評估節點自身重要度，但其主要應用于無權網絡。而高速公路是復雜、動態變化加權網絡，因而需結合交通流時空特性對拉普拉斯中心性法予以改進以適應高速路網。

基于此，現考慮交通流時空關聯特性[10]，利用皮爾遜相關系數[11]建立狀態關聯系數矩陣改進拉普拉斯中心性方法以評估自身影響，設計等效距離評估鄰居節點影響，融合節點自身及鄰居節點的影響，建立節點權重系數模型；并基于此建立反映路網交通狀態指數的綜合判別模型，以實現對時空分布不均的高速路網交通狀態的快速識別。

1 高速公路網絡狀態識別流程

研究對象為高速公路網絡，定義路段為節點，并將高速公路網絡劃分為純主線路段、含出入口匝道路段、含立交橋路段3種類型節點組成的集合，其狀態識別流程如圖1所示，基本原理如下。

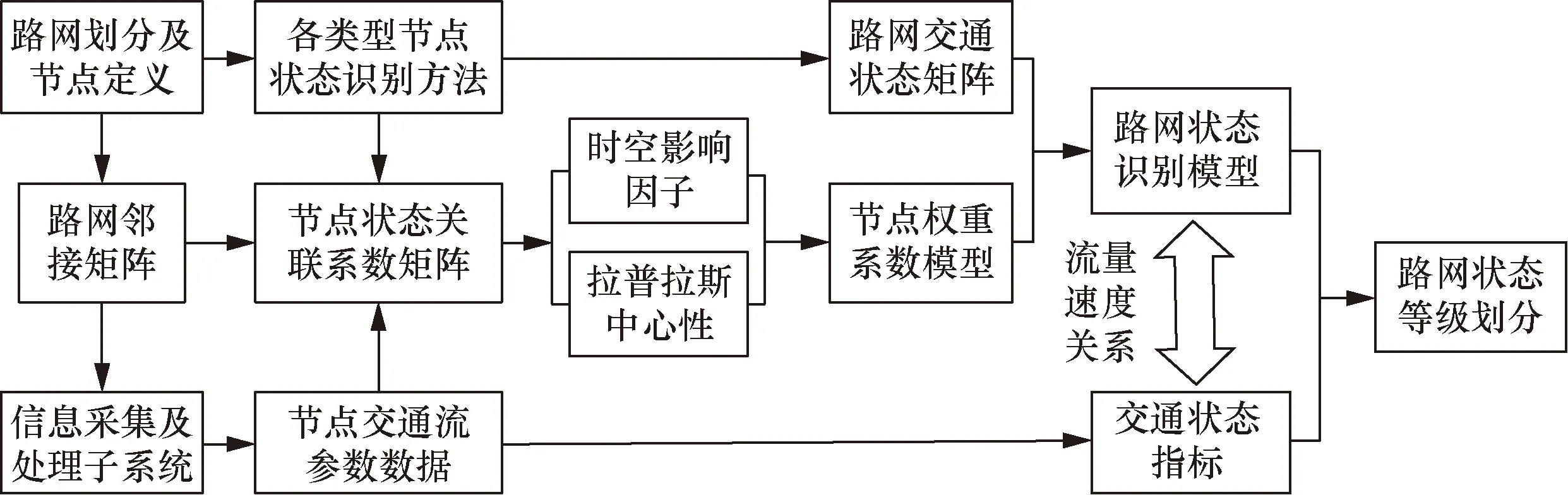
圖1 高速公路網絡交通狀態等級劃分Fig.1 Traffic state classification of freeway network

(1)信息采集及處理子系統實時獲取路網各節點(路段)的原始交通流信息，通過相關計算和處理，得到各節點交通流參數數據信息，如節點的流量、速度、通行能力等。

(2)考慮純主線節點(路段)、含出入口匝道節點、含立交橋節點交通流特性并分別建立符合其交通流特性的狀態識別模型，結合鄰接矩陣建立路網交通狀態矩陣。

(3)考慮節點狀態時空關聯性，采用皮爾遜關聯系數法，建立節點狀態關聯矩陣。利用節點狀態關聯矩陣改進拉普拉斯中心性方法確定節點自身重要性，設計時空影響因子評估鄰居節點狀態影響，融合節點自身及鄰居節點影響，建立節點權重系數模型以區分不同節點對路網運行狀態的差異性。

(4)利用路網交通狀態矩陣和節點權重系數模型建立高速公路網絡交通狀態模型，并結合成熟評價指標劃分區域路網交通狀態等級。

2 網絡交通狀態識別模型

2.1 網絡拓撲描述

拓撲可以用來表示空間對象間的鄰接關系。將已劃分好的高速公路網絡用G(N,A)表示，其中，N為節點集；A為邊集，表示對應節點間是否相鄰；aij為其元素，其值為1表示節點i和j相鄰，為0表示不連接。通常某個節點會影響k階相鄰節點，其k階可達空間鄰接矩陣W[12]表達式為

W=Bool[(An×n+In×n)k]

(1)

式(1)中：An×n為鄰接矩陣；In×n為單位矩陣；Bool(·)函數表示矩陣計算采取布爾代數運算規則。

2.2 節點狀態識別模型

(1)純主線節點(路段)。不受出入口匝道影響的純主線路段因地理位置、車道數等會使限速、流量和通行能力存在差異。建立其交通狀態識別指標模型為

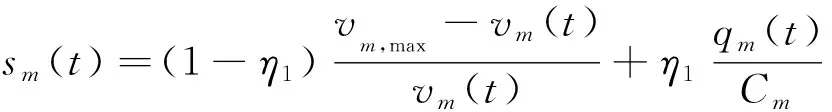
(2)

式(2)中：sm(t)為t時主線節點m交通狀態指標值；η1為指標重要性權衡，η1∈[0, 1]，根據實際情況選取，此處取0.5；vm,max和vm(t)分別為t時m的最大限速和平均速度；qm(t)和Cm分別為t時m的檢測流量和通行能力。

(2)含出入口匝道節點。對于一段主線和其連接的出入口匝道而言，存在加減速頻繁、通行能力下降等問題。據王曉[13]研究，修正分流區通行能力Cz,f和合流區通行能力Cz,o以體現分合流區的狀態影響。建立其狀態指標模型為

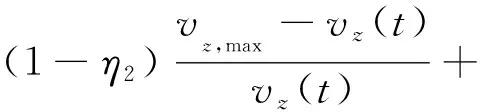
(3)

式(3)中：sz(t)為t時考慮分離和交匯連接節點z交通狀態指標值；η2為指標重要性權衡，η2∈[0, 1]，根據實際情況選取，此處取0.5；vz,max和vz(t)分別為t時節點z最大限速和平均速度；qz,f(t)、qz,m(t)和qz,o(t)分別為節點z的分流區流量(分流點上游主線與分離量之差)、主線流量和合流區流量(合流點上游主線與匯入量之和)。

(3)含立交橋節點。類似于出入口匝道節點，也要考慮分離和匯入問題。其可以看作是兩個方向上的出入口匝道節點的組合，故取其狀態指標值的均值以表示該節點的交通狀態。

2.3 網絡交通狀態矩陣

依據路網空間拓撲結構和t時計算的節點交通狀態值，建立路網鄰接交通狀態矩陣Sij(t)，表達式為

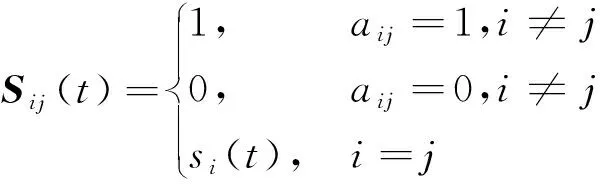
(4)

式(4)中：si(t)為高速公路網絡劃分為的不同類型節點i的狀態指標值。

3 基于改進拉普拉斯中心性的網絡狀態識別模型

3.1 狀態時空相關性

高速公路交通流時空分布特性使路網中節點間的狀態存在時空關聯性，關聯性越強表明節點之間狀態聯系越緊密。皮爾遜相關系數(Pearson correlation coefficient，PCC)可以度量任意兩組對象X和Y在給定時間延遲s下的關聯性R，表達式為

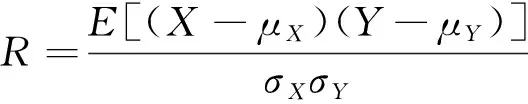
(5)

式(5)中：μX、μY為X、Y的均值；σX、σY為X、Y的方差。

節點間狀態的影響不僅體現在時間維度，也體現在空間維度，引入等效距離因子Cij(t)來表示節點i與j的狀態空間相關性，表達式為

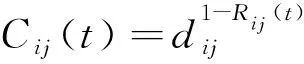
(6)

式(6)中：dij為節點i與j間物理距離；Rij(t)為利用式(5)得到的t時節點i與j的狀態相關系數。距離越遠，影響越小，因而，Cij(t)與距離成正相關，與節點狀態相關程度呈負相關，符合實際交通流情況。

3.2 權重系數模型

不同節點對路網交通運行狀態存在差異性，其重要程度既要考慮自身重要性，也要考慮位置因素的鄰居節點的影響。

3.2.1 節點自身影響

拉普拉斯中心性法常用于評估節點自身重要性，其主要適用于無權網絡，拉普拉斯中心性越高，則節點自身重要度越高，而高速公路是復雜且動態變化的加權網絡，利用傳統方法計算鄰接矩陣A和度矩陣D并不合適，基于此，利用節點的狀態關聯矩陣構建加權鄰接矩陣AR(t)和度矩陣DR(t)，并對其進行改進，得

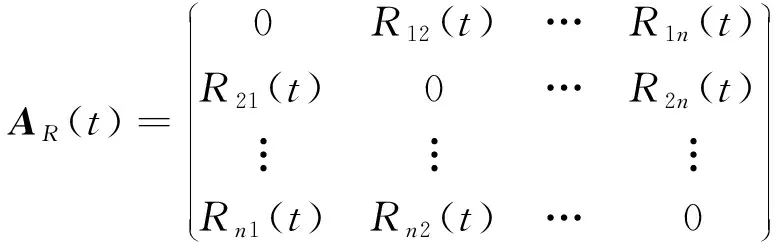
(7)

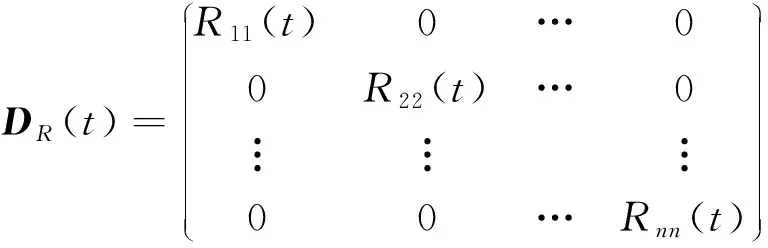
(8)

利用改進鄰接矩陣和度矩陣計算拉普拉斯矩陣LR(t)見式(9)，依據拉普拉斯矩陣得到拉普拉斯能量EnL(t)見式(10)。去除目標節點后重新計算拉普拉斯能量得到該節點自身中心性CnL(t)，表達式為

LR(t)=DR(t)-AR(t)

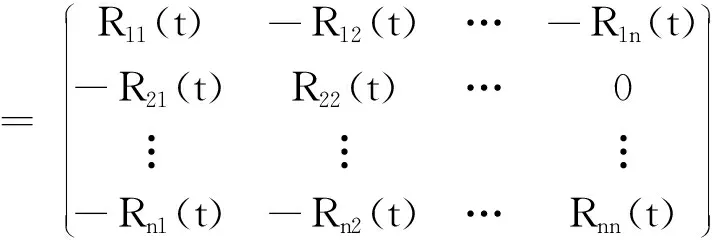
(9)

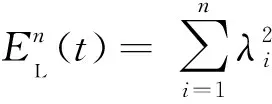
(10)

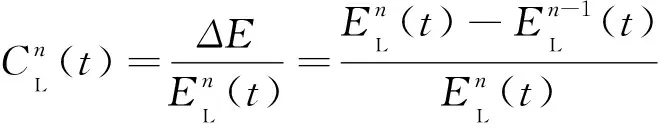
(11)

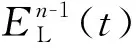
3.2.2 鄰居節點影響

路網是連通的，鄰居節點間必然存在影響。為進一步體現鄰居節點間的狀態傳播影響，定義狀態相關系數與等效距離的比值為鄰居節點的時空影響因子Kij(t)。當兩節點間等效距離Cij(t)變長，空間影響減弱，呈負相關；狀態關聯系數越大，影響越大，成正相關。因此，Kij(t)越大，表明影響越大。表達式為

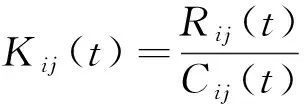
(12)

節點的影響取決于節點自身及鄰居節點在路網中所起到的作用。因此，通過融合節點自身影響系數及鄰居節點影響系數構建節點權重系數模型(node weight model，NWM)。其中，節點自身影響系數為αi(t)，表示節點本身影響占路網總的節點影響的比值見式(13)，鄰居節點影響系數為βij(t)，表示鄰居節點影響占路網全部鄰居節點總影響比值見式(14)，節點權重系數矩陣I(t)見式(15)。

(13)

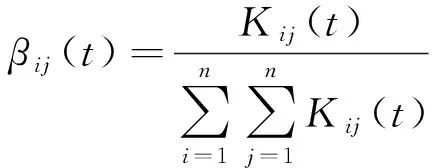
(14)

(15)

3.3 路網狀態識別模型

依據道路拓撲，計算各節點交通狀態值及路網各節點權重系數，建立路網交通狀態識別模型見式(16)，并對指標進行標準化處理見式(17)。

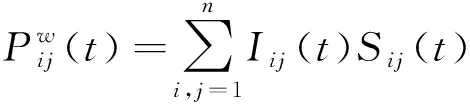
(16)

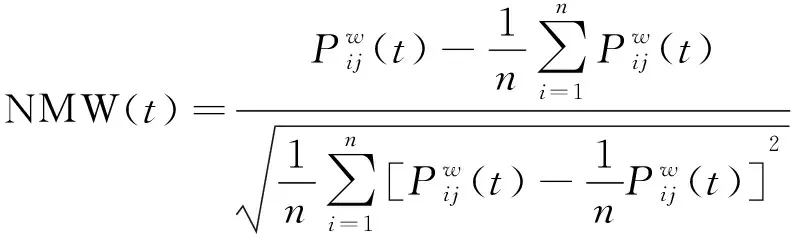
(17)

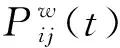
4 仿真實驗

4.1 實驗對象

以河北省保定市京港澳高速徐水—清苑的一段高速公路網絡為實驗對象，為繞城高速東環線，其存在多種類型路段，臨近市區，時空分布不均特性明顯。具體見圖2所示。該路網含6個出入口匝道對(一個入口匝道對應一個出口匝道)和2個與其他高速連通的互通式立交橋，主線雙向八車道，長度為48 km，大小車限速分別為100 km/h和120 km/h，大貨車比例為35%。依據是否包含出入口匝道、立交橋為依據劃分該路網為18個節點，各節點對應的主線長度如表1所示，仿真實驗使用數據為VISSIM通過實際調查數據和仿真對模型校驗和參數優化所得。

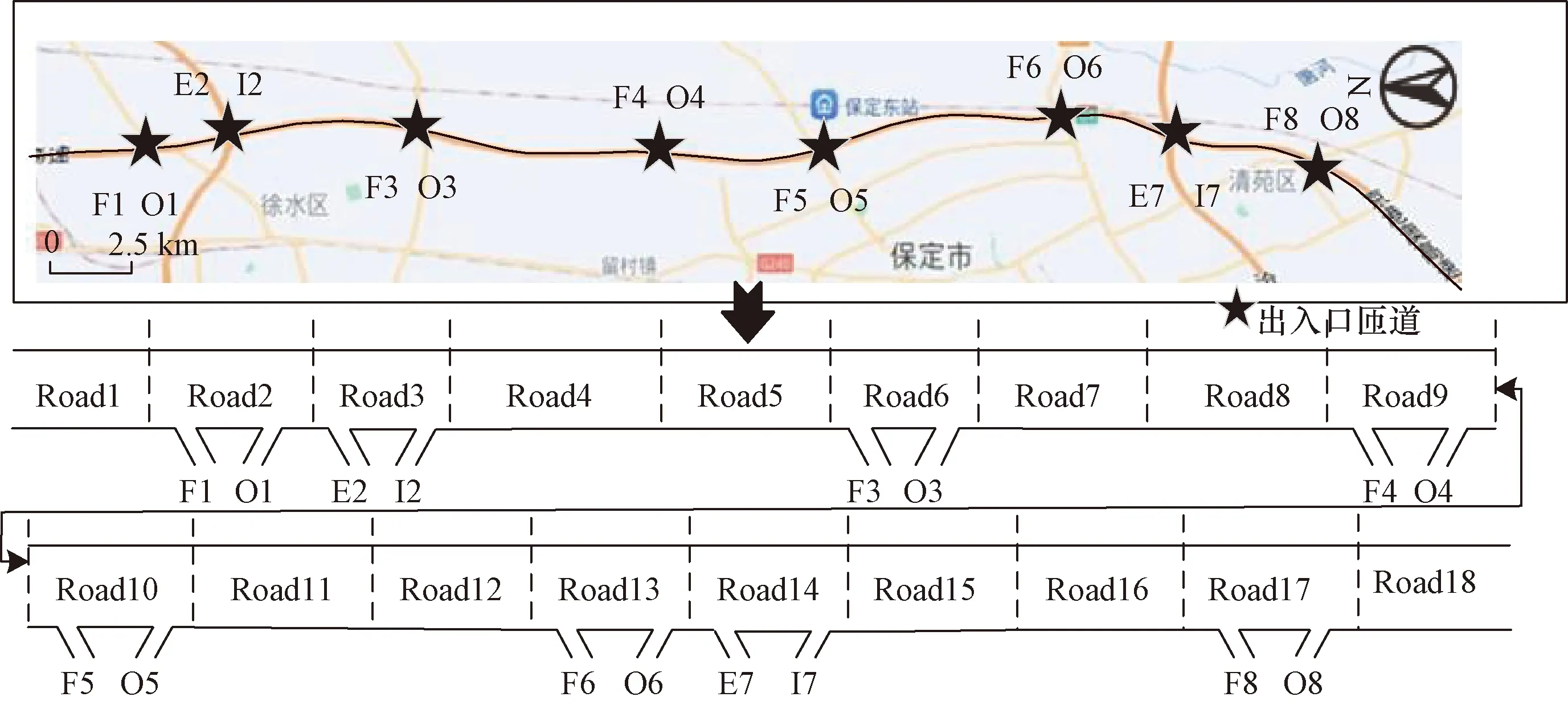
O為入口匝道，F為出口匝道，I為互通式立交橋入口匝道，E為互通式立交橋出口匝道；數字序號為節點編號圖2 仿真高速路網及其拓撲圖Fig.2 Simulated freeway network and its topology

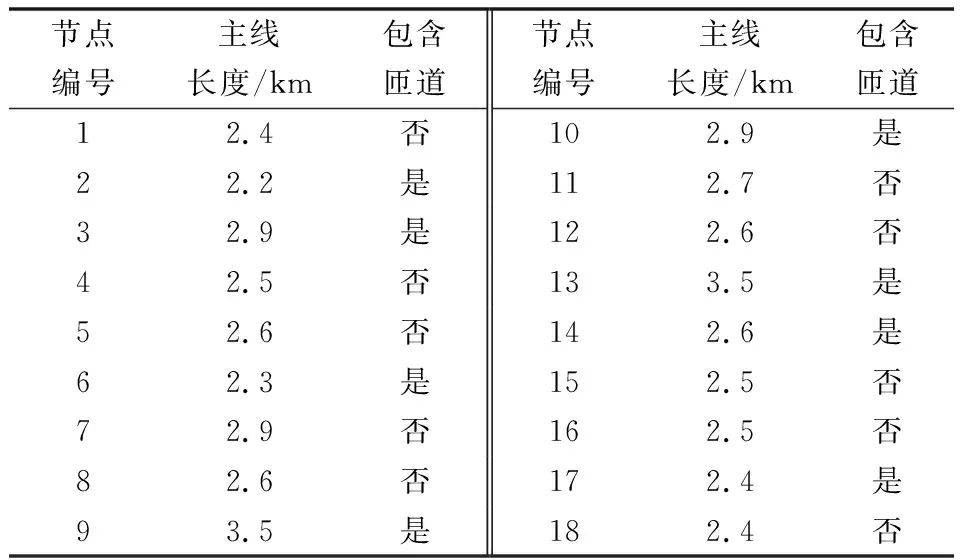
表1 高速路網節點劃分及長度Table 1 Division and length of nodes of freeway network

4.2 情景設置及分析

為模擬高速公路時空分布不均性，驗證該狀態識別方法的判別效果，設計4種交通場景，通過不同時間段匝道加載進入路網交通量不同來體現節點的時空狀態差異性，每次仿真3 h，通過在相應位置設置檢測器來獲取交通流參數數據以便后續計算，數據采集時間間隔為10 min。

情景1：路網整體交通需求一般，各入口匝道每小時分別加載高峰時段60%、70%和50%的交通量。

情景2：節點1～9交通需求較大，節點2、3、6、9入口匝道每小時分別加載高峰時段70%、80%和75%的交通量，其他入口匝道各小時分別加載高峰時段60%、70%和50%的交通量。

情景3：節點10～18交通需求較大，節點10、13、14、17入口匝道每小時分別加載高峰時段70%、80%和75%的交通量，其他入口匝道各小時分別加載高峰時段60%、70%和50%的交通量。

情景4：路網整體交通需求較大，各入口匝道每小時分別加載高峰時段70%、80%和75%的交通量。

利用仿真得到各節點平均車速、流量等參數，基于Python編寫程序計算各節點狀態值和狀態關聯度值，選取某次仿真部分節點狀態關聯性值(節點2、3、4、13、14、15)如圖3(a)～圖3(d)所示。

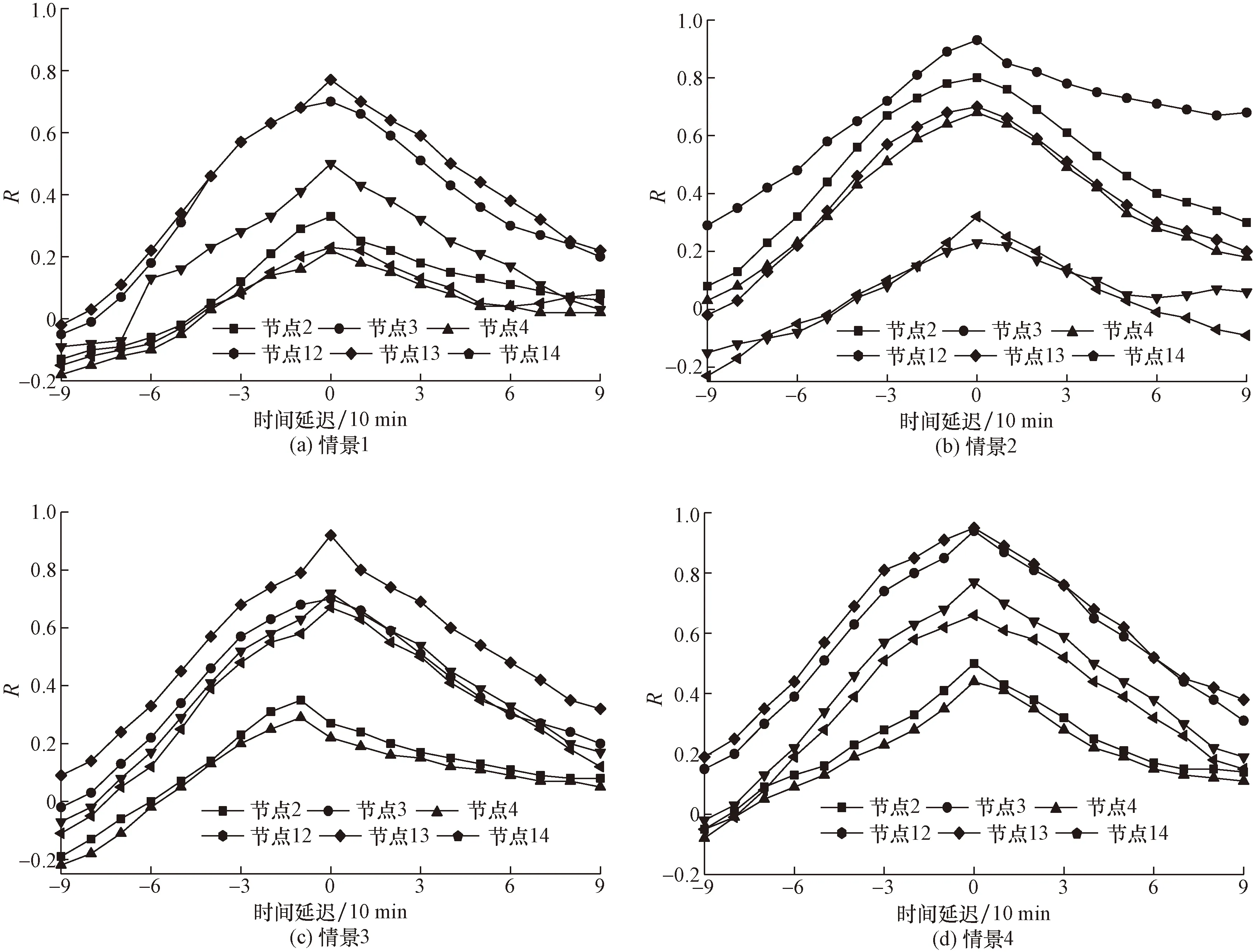
圖3 不同情景下部分節點關聯度Fig.3 Correlation value of some nodes under different scenarios

不同交通需求情景下，同一節點狀態時空關聯性存在差異。同一交通需求情景下，不同節點狀態時空關聯性存在差異，節點3、14關聯性最強，為關鍵節點，是因為其作為交通轉換樞紐，與各方向交通流關系緊密所致。

含匝道節點狀態關聯值比純主線節點高，是因為出入口匝道與主線干擾使狀態波動對上下游節點狀態造成較強影響。

當區域交通需求增加，相應區域時空關聯性增強，與關鍵節點距離越近的節點時空關聯性越強，同樣是因為流量增加使得區域交通狀態發生改變，整體波動性增強，對其他節點狀態影響程度加深所致，符合實際交通情況。

綜上所述，高速公路網絡交通流時空分布不均特性及節點交通流特性差異使得節點狀態關聯程度存在差異，即節點狀態存在時空差異性，各節點對路網運行狀態影響程度不同，凸顯了建立節點權重系數模型的必要性。

仿真軟件Vissim可得到路網中相關的評價參數，如路網平均車速、總停車延誤、排隊長度等指標。基于本文提出的路網交通狀態識別模型與采集到的相關指標，根據軟件輸出得到仿真路網不同交通情景下第2仿真時下6個時間段的仿真狀態參數見表2，并得到某次仿真路網不同交通情景下數據采集時間間隔下的狀態識別平均運行時間分別為0.176、0.191、0.188、0.207 s，表明了方法可以快速有效地識別狀態。

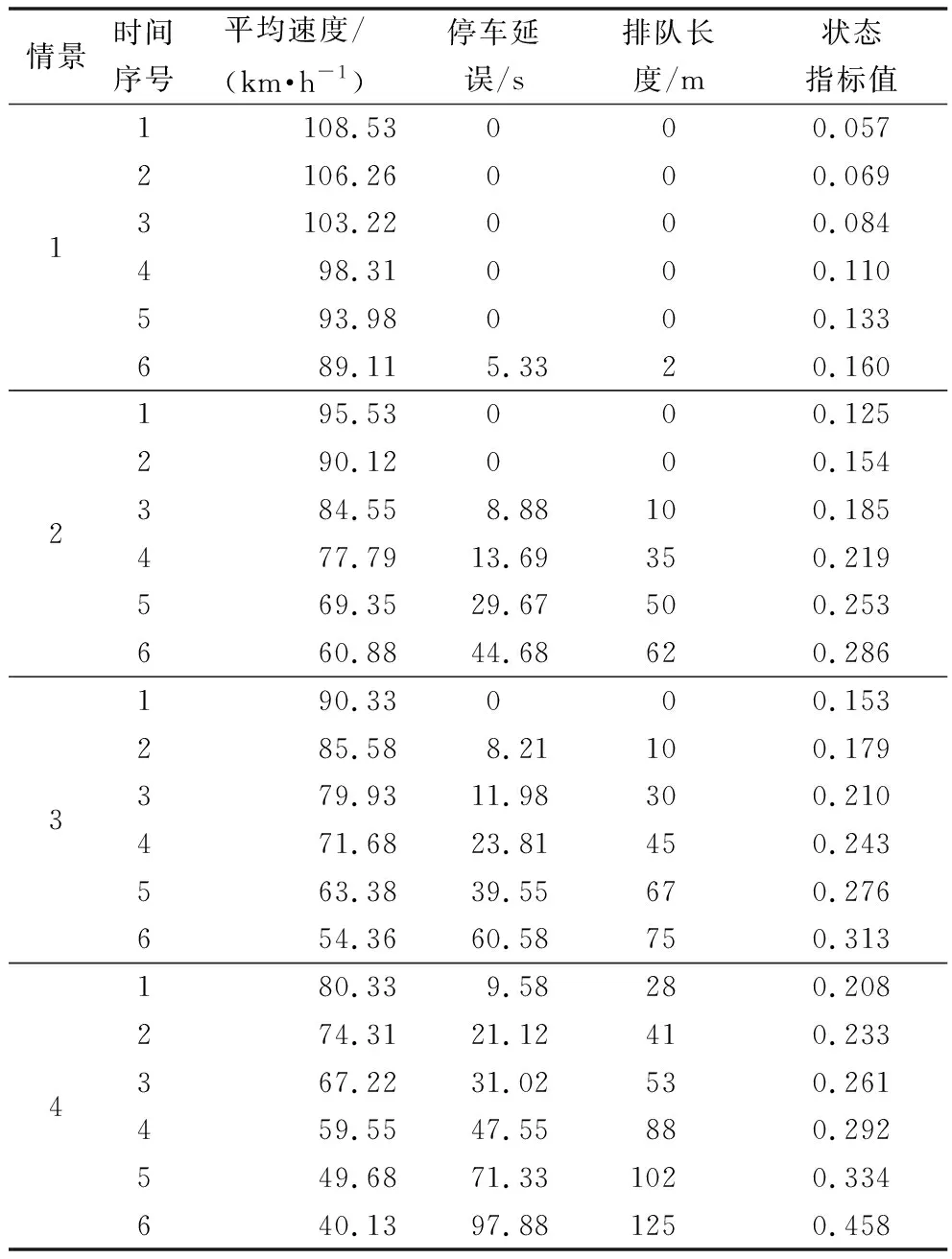
表2 高速公路網絡交通狀態參數Table 2 Traffic state parameters of some nodes of freeway network

在不同交通需求下，從仿真結果可以發現：模型識別速度較快，能夠滿足實際需要；當高速公路網絡交通需求低時，路網平均速度快，路網狀態NWM小，停車延誤低、排隊長度短，表明路網交通狀態良好，基本不存在擁堵；當路網交通需求增加后，路網狀態NWM增大，車輛平均速度降低，延誤增加，排隊現象出現且不斷增加，路網出現擁擠，若不控制隨時間繼續加劇，符合實際運行情況，表明了狀態識別方法的可行性。利用平均速度結合NWM來劃分區域路網交通狀態等級，基于成熟的評價指標[14]將路網交通狀態劃分為5個等級，分別為暢通、基本暢通、輕度擁堵、中度擁堵、重度擁堵，各指標劃分等級范圍如表3所示。

表3 高速公路網絡交通狀態等級劃分Table 3 Classification of traffic state of freeway network

4.3 與其他方法對比分析

由于交通流的時空分布不均性帶來的節點差異性，為進一步體現所建立的高速公路網絡交通狀態識別模型NWM的實時和準確性，依據不同情景的交通需求差異性，將路網劃分為2個子區域，其中節點1～9為子區域1，10～18為子區域2，為提高實驗準確性，使結果更具說服力，3種算法均重復執行仿真50次，且不同交通情景下數據采集時間間隔下的狀態識別平均運行時間分別為0.172、0.189、0.188、0.205 s。所提出的NWM方法與交通運行指數法(traffic performance index，TPI)和車輛行駛時間法(vehicle hour traveled，VHT)在不同交通情景下的子區和路網狀態識別準確率見表4。

表4 不同情景與方法的子區域與路網狀態識別準確率Table 4 Sub region and network state recognition accuracy rate of different scenarios and methods

TPI方法對交通需求大的子區狀態識別較精準，對路網整體狀態識別精準性不足，穩定性差。

VHT模型對比TPI模型對路網的狀態識別稍精準，穩定性有所提升，但子區識別狀態誤差稍高，對于交通流的時空分布不均的適應能力不足，實時性不足。

NWM方法在穩定性和實時性方面表現均優于其他方法，尤其是當交通需求較大時，對比TPI模型，對于含匝道節點3和純主線節點4，NWM模型準確性可提高約9.7 %和7.1 %，可見NWM模型能適應交通流的時空分布不均性；對路網的狀態識別精準度，不同交通情景下，NWM模型最優，VHT模型次之，TPI模型最差，表明了本文方法能適應不同的交通需求，充分體現了本文方法優越性。

綜上所述，NWM模型可充分利用節點狀態的時空差異性，快速有效識別子區域和路網的交通狀態。

5 結論

充分利用高速公路網絡結構布局差異性和交通流時空分布不均性，考慮了高速公路主線、出入口匝道、立交橋等節點的交通流特性建立了相應的狀態識別方法，基于節點狀態的關聯性，改進拉普拉斯中心性方法和構建時空影響因子以評估節點自身及鄰居節點影響，建立了符合高速公路網絡特點的權重系數模型，進而建立了高速公路網絡狀態識別模型。根據仿真實驗結果，得到如下結論。

(1)高速公路網絡由于時空分布不均性和各節點的交通流特性的差異，使得路網中不同節點間的狀態關聯程度差異明顯，基于節點時空差異性建立的權重系數模型能夠充分體現節點對路網運行狀態的影響程度，為路網的交通狀態識別提供一定理論基礎。

(2)考慮節點差異性的高速公路網絡狀態識別方法，對比TPI和VHT模型在識別的穩定性和實時性均有一定程度提高，針對不同交通需求的子區域狀態識別精確性也優于另外兩種方法，表明該方法可以快速有效識別高速公路網絡和子區域的狀態，識別結果可為路網交通管理與控制提供依據。