機坪管制移交后機場運行控制中心大廳人員動態排班優化

陳華群，柳藴棲，熊靜，朱興澳

(中國民用航空飛行學院空中交通管理學院，廣漢 618307)

2013年，民航局啟動了機坪管制移交工作，經過近十年的不斷推進，主要樞紐機場已基本完成了機坪管制移交工作。原有的機坪指揮席位從機場運行控制中心(airport operational control center，AOCC)分隔出來，單獨設置機坪塔臺，其職能由以前的機場指揮中樞轉變為運行協作保障和應急管理。大廳采用24 h不間斷工作制度，當前人員排班采用人工經驗形式、高峰值滿足模式，而不同運行時段航班保障任務卻呈現動態變化，容易造成工作負荷分布不均，早晚班分配均衡性差。因此，優化AOCC大廳的排班方式，有利于保障運行安全，降低成本，提高運行效率和服務水平。

AOCC大廳人員排班屬于指派問題范疇，當前的研究多聚焦于人員的管理措施[1]，管制移交后的動態智能排班并未涉及。可借鑒的員工排班涉及醫學類的護士[2-3]、鐵路行業的乘務員[4-6]、社會救援服務的呼叫員[7]等不同領域，分別提出了需求矩陣法、基于優先級自動排班算法、回溯算法、遺傳算法、模擬退火算法等優化人員排班。國內外學者們對民航業的排班優化，大多注重機場管制的排班評價、地服人員的排班和系統框架搭建，如：Billy等[8]面向服務于定期和非定期空中交通流量，提出運用人工智能技術建立面向偏遠塔臺的員工優化排班的系統框架；Lü等[9]利用文本挖掘方法，建立包含4個準則要素和25個子準則指標的評價體系，運用采用層次分析法和模糊綜合評價方法對機場停機坪運營管理現狀，指出了機場運行人員因素是管理核心；曹藝林[10]根據服務旅客的數量分布規律建立員工需求預測模型，采用改進變鄰域搜索算法實現動態排班模型，減少值機等待時間，提高排班效率；盧敏等[11]運用block Gibbs抽樣迭代優化班型內地服人員構成、班型內航班集和班型生成，既滿足了班組資質，又均衡了白夜班的動態排班。上述研究方法為論題提供可行依據，但更需結合管制移交后的AOCC大廳的崗位職能變更，進行優化目標設定和動態求解算法改進。

AOCC大廳人員的動態排班不僅決定著航班運行保障的安全，而且關系整個中心的全局協調和應急響應的成本。因此，現基于航班動態保障需求建立一套智能的人員動態排班方法，擬構建多目標排班模型，利用遺傳算法特性傳承手工排班的優良父輩，通過改進交叉、變異算子實現組合優化，從而提高AOCC大廳人力資源利用率，降低員工疲勞度，提升滿意度。

1 動態智能排班的原則

傳統的AOCC大廳手工排班是行政人員按照最大航班峰值，固定班組人數生成靜態輪班班次，人工干預較強。提出的AOCC大廳員工動態排班是指根據當前的人力資源情況、班次保障要求、排班規則及優化目標生成排班表。班次保障要求指該班次起始時間、結束時間以及該班次需要的員工資質類型都滿足要求。優化時遵循的原則如下。

(1)班組資質水平。因教育、學習和經歷等多因素會導致不同員工對同一崗位任務的熟練程度不同，將經驗、資歷4年以上的員工作為精英員工，其余則為普通員工。

(2)班組早晚班輪換。為保證員工滿意度，每個班組一周內的排班方案，使得每個班組早晚班滿足均衡，以便均衡員工疲勞數值。

(3)班次資質需求。由于機場上班時間的特殊性，早班和晚班班組中至少一名精英帶領普通員工在值班，且班次需要的員工資質和數量須得到滿足。

(4)工作時長均衡。從公平性的角度，每個班組每周的總工作時長需要保持接近，且各個員工之間時長方差要達到最小。

2 AOCC大廳人員排班多目標模型

擬構建的多目標排班優化模型遵循安全、經濟、均衡和公平的原則；首先確保所有班次被符合資質要求的人員覆蓋，再尋求使所有班組的人力成本最小化的經濟性，然后兼顧班組員工的早晚班疲勞值和各班組總工作時長的均衡性。

2.1 參數設定與決策變量

為了方便問題模型和算法的描述，定義參數和決策變量符號如表1所示。

表1 參數定義Table 1 Parameter definitions

2.2 多目標函數的確定

AOCC大廳排班優化問題是在符合排班規則前提兼顧經濟性、公平性及合理性，指派合理的班組在合適的班次執勤。因此，根據2.1節設置的基本參數和決策變量，建立目標函數如下。

2.2.1 排班人力成本

在確定每天具體的班次中，需要班組到具體班次中，且早班、晚班的成本也會不一樣，排班過程中需使得人力成本最低，其目標函數用f(1)表示為

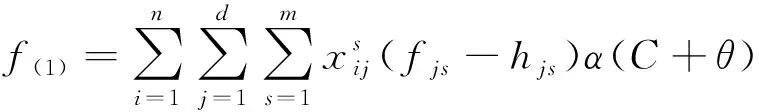
(1)

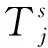
2.2.2 班組早晚班次疲勞數值

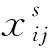
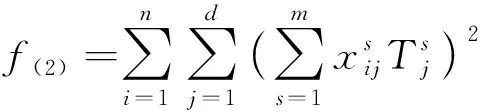
(2)

2.2.3 班組工作時長均衡性

滿足所有班次的任務都被覆蓋后，安排班組到具體班次，為縮短班組工作時長，則最小化班組的總工作時長，但考慮到工作時長均衡性方面，每個班組目前工作時長與該班組平均需要的工作時長之間的方差，方差越小則表示工作時長越均衡。其目標函數用f(3)表示為

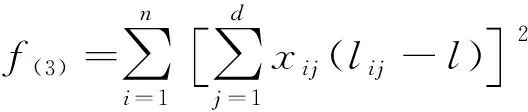
(3)

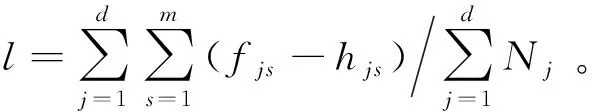
2.3 多目標排班數學模型

結合2.1節參數設定以及2.2節目標函數的分析建立AOCC大廳人員多目標排班模型描述如下。

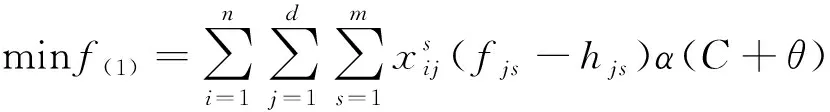
(4)

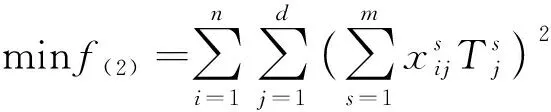
(5)

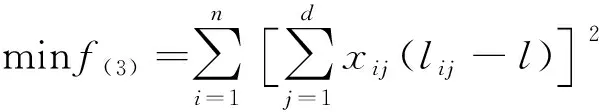
(6)

班組排班具體約束條件如下。

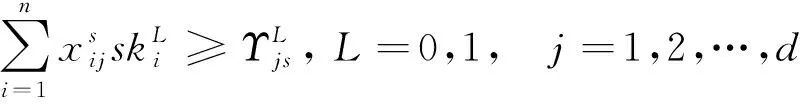
(7)

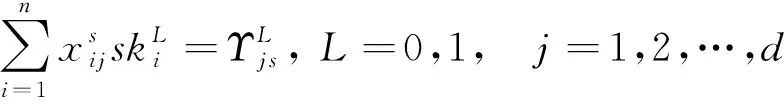
(8)

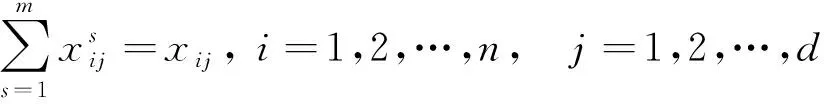
(9)

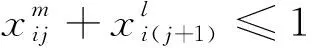
(10)

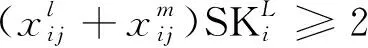
(11)

xij≤xi

(12)

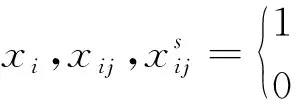
(13)

式(7)表示任何一個班組中資質總人數要大于等于需求人數；式(8)表示該班組資質人員數應該恰好滿足要求，防止該班組因資質不達標而不排早晚班；式(9)表示第j天執行的班組i需要當該日某具體班次；式(10)表示班組i在連續兩天內早班和晚班不能超過2個；式(11)表示第j天的早班和晚班執行的班組至少有一個高資質員工帶班；式(12)在某一周內班組i至少上班1 d。

3 改進遺傳算法的多目標模型求解

由于上述所求模型是復雜的0-1多目標整數非線性規劃問題，且需要考慮多個目標同時優化，如果直接求解十分困難[11]。因此，采用基于非支配排序遺傳算法的改進算法[12]，改進方向為動態調整交叉和變異概率[13]。決策者會隨機選取交叉、變異默認范圍內的數值，而交叉、變異概率數值的選取對遺傳算法的尋優能力影響很大[14]，但實際情況中排班需要快速、及時更新結果，為快速尋優，提高計算機收斂速度，構建動態交叉Pc和變異概率算子Pm，表達式分別為

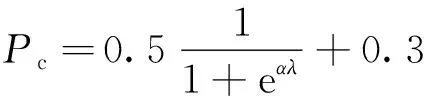
(14)

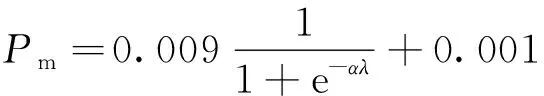
(15)

式中：λ為迭代系數，λ20n/(nmax-1)-[10(nmax-1)+20]/(nmax-1)，nmax為最大迭代次數，n為當前迭代次數；α為縮放系數。根據遺傳算法思想，提出繼承優良父輩、動態交叉、概率變異和精英保留的迭代算法計算最小成本、時長方差和疲勞值,算法具體改進步驟如下。

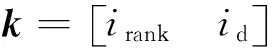
步驟2產生初始種群。每一條染色體對應基因片段x、y、f、k，即每一個班組指派某一個班次成功后對應一條染色體，隨機產生規模大小為N的初始班組種群，記為初始父代種群P0，并將隨機產生的初始可行排班方案存儲到矩陣變量Zj中。

步驟3目標函數值計算。隨機產生的班組種群完成指派后，統計編號xi的班組執行的班次情況，并對該班組個體的成本f(1)、早晚班疲勞值f(2)、工作時長方差f(3)進行函數值計算，存儲片段f中。

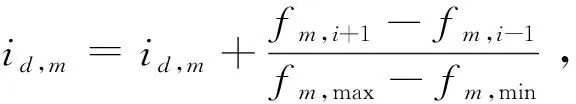
步驟5自適應交叉、變異操作。針對根據自適應的交叉、變異概率，若該個體滿足調整后的交叉、變異概率，則進行交叉、變異操作。

步驟6種群合并。將初始父代班組種群P0與交叉變異后的子代班組種群P1進行合并，班組種群規模大小為2N，對合并后的種群P2按照步驟4方法再進行非支配排序與擁擠度計算，得到所有班組個體的非支配序irank和擁擠度id，存儲到片段k中。

步驟7保留精英個體。基于合并后的新種群P2中所有班組個體的非支配排序大小，按照擁擠距離由大到小的順序保留種群規模為N的班組個體，產生新的種群P3，至此將新的種群P3對應的排班方案存儲到矩陣變量Zj中。

步驟8迭代尋找最優解。返回步驟4，進行下一次的排序、擁擠度、自適應度交叉、變異計算，直到滿足最大迭代次數，找到該算法下pareto最優解集圖，提取出每一個解所對應的每一套排班方案的解集信息f(1)、f(2)、f(3)。

步驟9從得出的pareto最優解集中選擇一個最優方案，即提取所對應的矩陣變量Zj，并繪制出該方案下的排班表，生成Excel報表，排班結束。

基于MATLAB平臺，實現改進遺傳算法的動態排班流程如圖1所示。

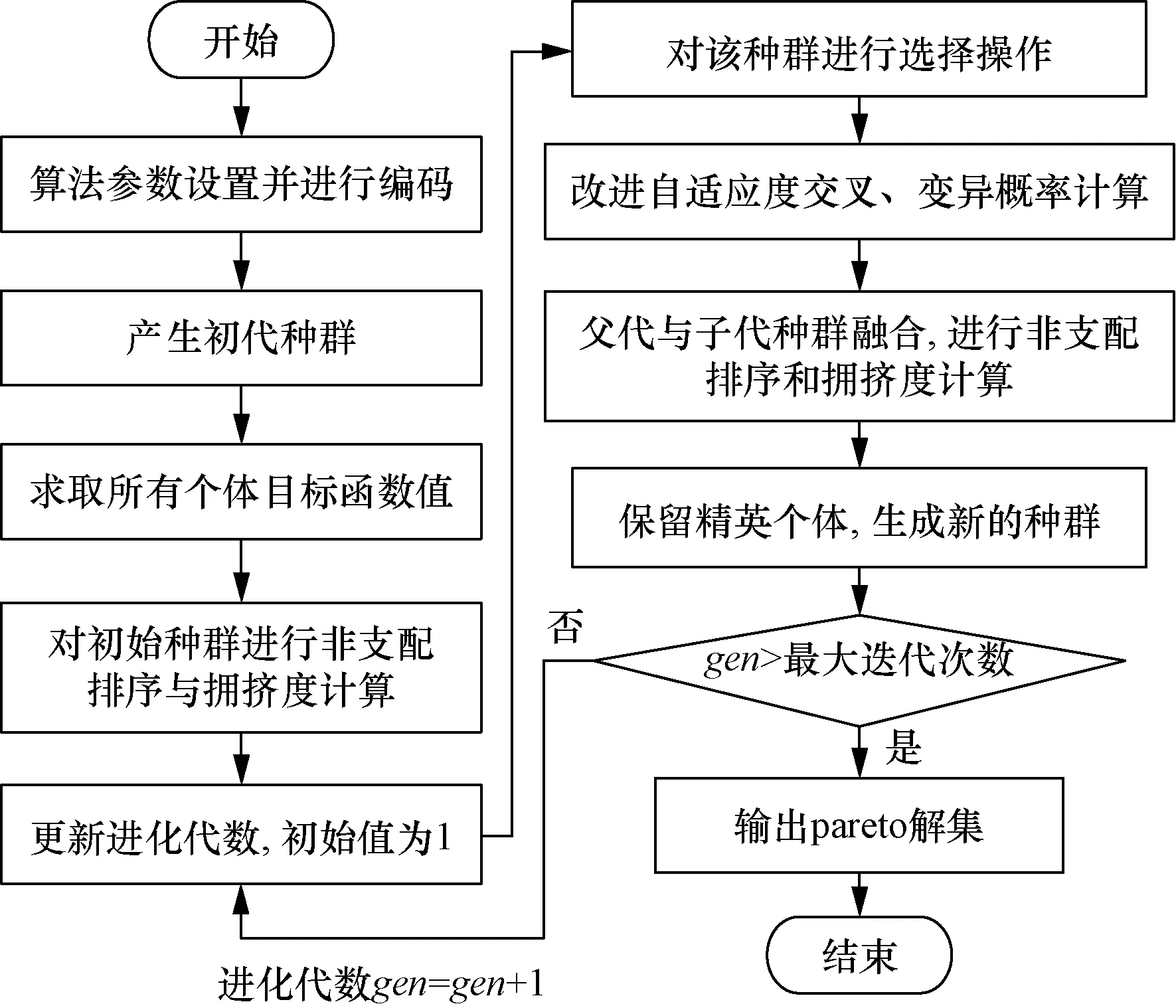
圖1 改進遺傳算法流程圖Fig.1 Improved genetic algorithm flowchart

4 實例仿真

選取西安咸陽機場管制移交后的AOCC大廳人員排班進行實例驗證，航班選取為2021年12月14—20日一周的起降架次，種群規模N=30，最大迭代次數設置為200。

4.1 參數選取

西安咸陽AOCC大廳人員排班采用手工方式，安排模式如下。

(1)每天工作時間為6:00—次日6:00，6:00—8:30和22:00—次日6:00+屬于加班時段，早班1時段6:00—8:30，白班2時段8:30—11:30，白班3時段11:30—14:30，白班4時段14:30—17:00，晚班5時段17:00—22:00，夜班6時段22:00—次日6:00共6個時段4個班種，班次和班種實際情況如表2所示。

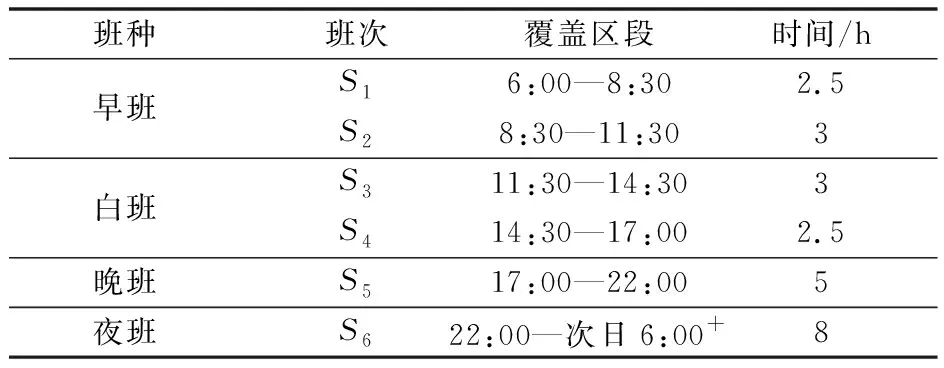
表2 西安咸陽AOCC大廳班種和班次情況Table 2 Class type and frequency of AOCC in Xianyang

(2)普通員工21人，值班主任3人，分為3個班組，每個班組平均配備7名員工、1名值班主任。

(3)采用上1休2排班模式，共有3個班組進行輪班，在值班期間工作人員不能離開機場，以防出現高峰時段人手不足的情況。下班休息48 h后恢復上班，每3 d一個周期，每天的22:00—次日6:00由于航班數量少，人力需求也少，屬于加班時段。

4.2 多目標優化排班結果

結合第3節改進非支配排序遺傳算法的步驟，通過MATLAB編程進行迭代計算，得到了改進后遺傳算法的Pareto解集圖，如圖2所示。

圖2可知，改進算法后得出的解集較為集中，且目標函數值f(1)最高為10.8萬元，目標函數值f(2)最大為70，目標函數值f(3)最大為17%。由于該pareto解集中每一個解對應一套排班方案，基于該解集提取出每套方案所對應的解集信息，即總成本、班組早晚班疲勞數值、班組時長方差3個目標結果，如表3所示。

從表3解集信息可知：前pareto解集對應11套排班方案，對于機場來說，往往成本會是首先考慮的目標，結合f(1)、f(2)、f(3)的數值結果，故從上面10個解集中偏向f(1)目標函數選擇編號為7的排班表，成本最低只有10.4萬元，且班組早晚班數值為69，班組時長方差為10%。繪制編號7的排班方案如表4所示。

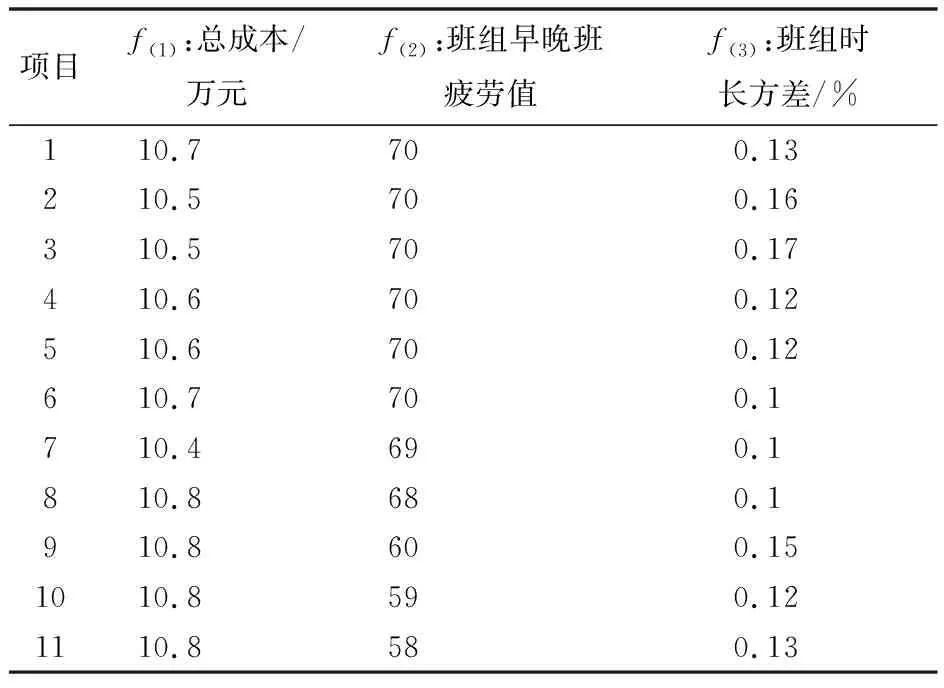
表3 改進后解集信息提取結果Table 3 Improved post-solution set information extraction

表4 改進算法后班組排班結果Table 4 Team scheduling results after improving GA

并且通過繪制Pareto解集中偏好f(1)目標函數解隨迭代次數的變化圖，如圖3所示。可以看出改進后的非支配遺傳算法可以使種群朝著偏好性目標快速進化，迭代次數大概在100就會收斂，既滿足決策者的偏好性，又使種群在整個維度充分進化。

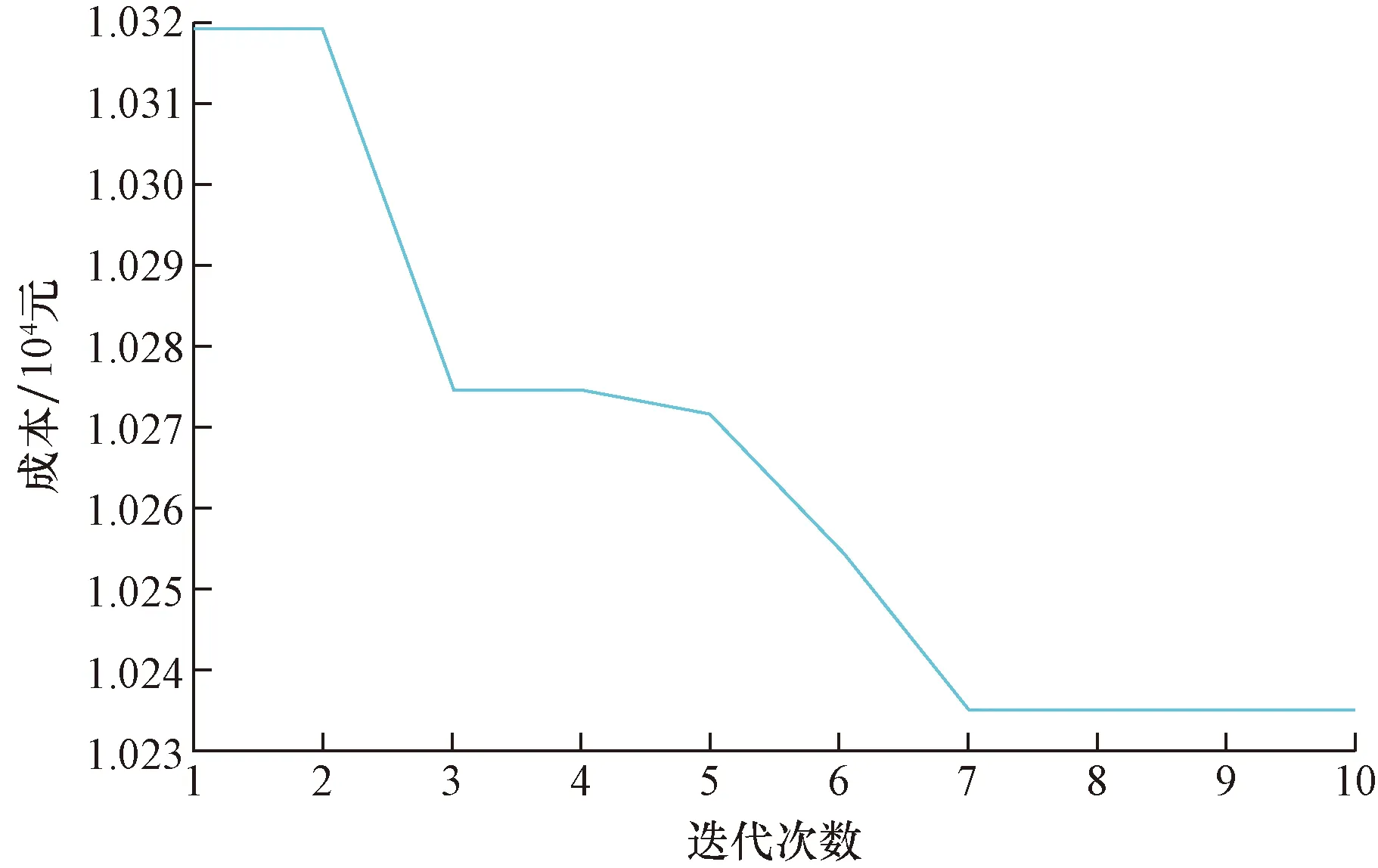
圖3 Pareto解集下偏好f(1)目標迭代結果Fig.3 Pareto solution sets the preferred f(1) target iteration results

4.3 傳統手工排班對比

已知該機場3個班組x1、x2、x3，目前采用上1休2排班班制，靜態排班“上1休2”模式中班組是固定人數，且該排班方式是按照3 d一個周期進行循環，但一周內的工作量因休息日、工作日的不同而不同，因此選擇一周的排班分析更具有代表性，咸陽機場傳統手工排班方式如表5所示。

結合《中華人民共和國勞動法》中規定的普通工作日加班的工資是平時的1.5倍，西安咸陽AOCC依照平均水平定義普通員工白班薪資為45元/h，加班時段為68元/h，組長按高資質員工60元/h，計算靜態排班上1休2模式下成本：x1=4.6萬元，x2=6.4萬元，x3=6.8萬元，總計17.8萬元。

根據表5排班方案計算3個班組一周的總工作成本、班組間時長方差和早晚班疲勞值如表6所示。

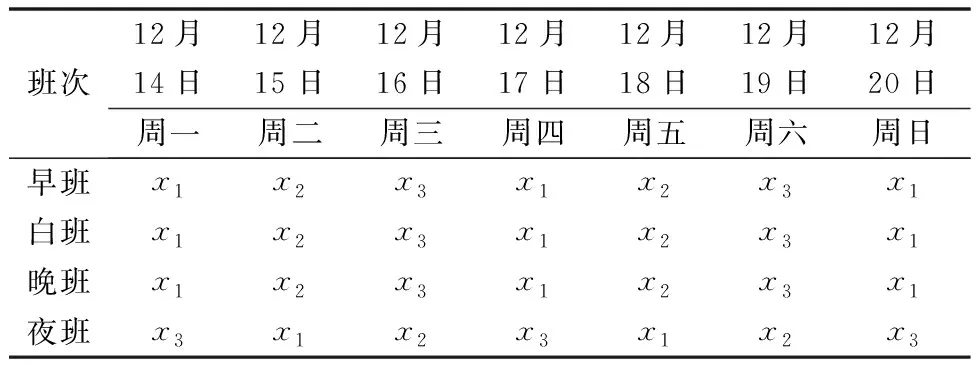
表5 西安咸陽AOCC大廳上1休2排班安排Table 5 An airport operation control center is arranged for 1 off and 2 shifts

由表6可知，上1休2班制模式下3個班組的早晚班疲勞數值相差較大，最低為20，最高達到41，故班組x3的早晚班排的較多，工作疲勞感比班組x2的工作疲勞感強，且班組間時長方差的高低使得3個班組排班均衡性不夠，x2班組時長方差最小為10%，表明班組2各員工之間工作時長均衡。

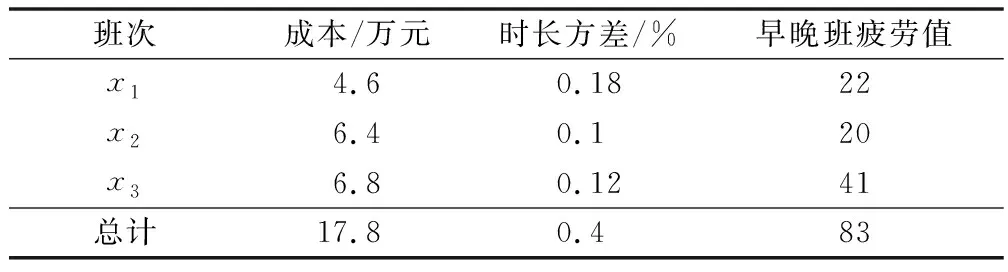
表6 上1休2排班班制一周的工作性能分析Table 6 Work performance analysis on a one-week shift system of 1 off and 2 shifts

4.4 禁忌搜索算法的排班對比

利用禁忌搜索算法從局部領域的擴展直至全局逐步尋優的特點，以傳統靜態排班結果作為給定的任意可行解x，Nl(x)(l=1,2,3)成為x的3個鄰域對應為增加、減少和取消排班，通過隨機提取方式產生候選集合。基于MATLAB仿真平臺的算法實現偽代碼如下。

Input?N[j]，SK[i]，X[i]，C[i])//基礎數據

Xij?Generate Ini Solution(N[j]→X[i])//初始解

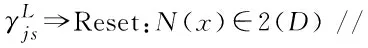
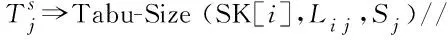
TabuLength?Round(hjs,fjs) //確定禁忌長度

void yuesefu1(int data[X],int result[S],int sum(L)) //判斷人員否在禁忌表內

f?Calculate (f(1),f(2),f(3))//評價函數計算

Tabu List(m,n)?Tabu List(m,n)-1 //更新禁忌表

Output?Best Schedule(N[j],X[i])//輸出最優X*

Until StopL=200 //滿足終止條件

將人員崗位資質匹配、時間沖突和排班喜好作為禁忌元素放入禁忌表中，這些元素下次搜索時將不會被考慮，禁忌長度即設定為3項；終止條件與改進遺傳算法相同，得到的排班結果如表7所示。

表7 禁忌搜索的班組排班結果Table 7 Team scheduling results of tabu search

因假設8:30—11:30時段必須由x1班組的值班主任參加例會，將其加入夜班禁忌表，額外增加了成本，費用如矩陣[式(16)]所示。此外，禁忌搜索算法只進不退的原則，導致x2夜班數量急劇增加。

(16)

將該AOCC大廳基于改進非支配排序遺傳算法求解所得的最優排班解為編號為7的方案，與傳統靜態、禁忌搜索排班的目標函數值進行對比，結果如表8所示。

由表8可知：相較于傳統靜態“上1休2”排班模式和禁忌設定，采用改進遺傳的智能排班總成本減少7.4萬元，時長方差減少33.3%，早晚班疲勞數值減少16.9%。

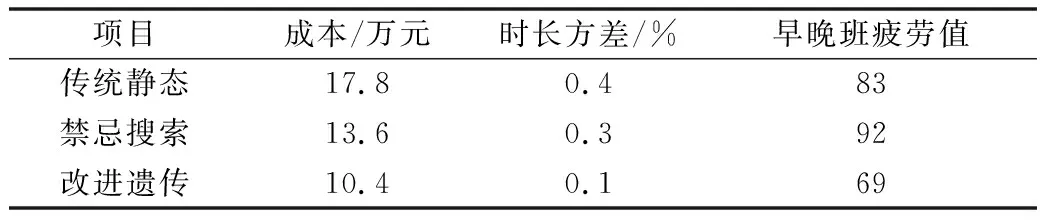
表8 傳統靜態與智能搜索排班結果對比Table 8 Comparison of static and intelligent schedule

5 結論

運用多目標規劃理論與人工智能算法解決機坪管制移交后AOCC大廳人員排班優化問題，確保所有班次被安全覆蓋，兼顧了人力成本、工作時長、晝夜班均衡和執勤疲勞度。主要研究結論如下。

(1)建立了以航班安全運行為中心的動態排班原則，實現了各班次在航班不同峰段的合理銜接,避免人員工作的干擾和重疊，提高工作效率。

(2)基于傳統靜態排班增加動態約束條件，從經濟、均衡、公平多角度建立多目標AOCC大廳人員排班模型，考慮排班流程中人員動態需求變化，增強排班靈活性。

(3)提出改進的非支配排序遺傳算法，有利于最優解集朝著更好的方向進化，降低了求解時間復雜度，符合排班快速響應的要求。

建立的人員排班以動態飛行任務為基礎，該方法適合員工數在50以內的中小運輸機場或通航機場；若運用于大型樞紐機場，可通過設定排班輪換周期，以降低搜索空間；員工的保障對象是立足于不同時段正常運行狀態的航班任務，未來需針對非正常情況進行特定約束限定。