內(nèi)置工字鋼圓端形鋼管混凝土短柱局壓性能的有限元分析

謝晉，李兵

(沈陽(yáng)建筑大學(xué)土木工程學(xué)院，沈陽(yáng) 110168)

考慮到橋墩結(jié)構(gòu)中多應(yīng)用圓端形作為橋墩的外形，以利用其抗沖擊、強(qiáng)弱軸特性，同時(shí)鋼管混凝土結(jié)構(gòu)作為較為完善的混凝土柱體改進(jìn)方式，在土木結(jié)構(gòu)領(lǐng)域中廣泛應(yīng)用。故對(duì)于圓端形鋼管混凝土柱的性能研究是橋梁領(lǐng)域研究中不可缺少的一部分。橋墩所受外力為橋梁支座傳遞的局壓荷載作用，故研究圓端形鋼管混凝土柱的局壓性能是極為重要的。隨著土木工程領(lǐng)域的不斷進(jìn)步[1-5]，結(jié)構(gòu)設(shè)計(jì)逐漸向高強(qiáng)度、高性能方向發(fā)展，故研究鋼管混凝土柱[6]的強(qiáng)化方式是該領(lǐng)域發(fā)展的重要一環(huán)。

在現(xiàn)階段研究中，李兵等[7]主要研究不同加載方式下圓端形鋼管混凝土短柱的應(yīng)力變化情況。沈奇罕等[8]主要研究圓端形鋼管混凝土短柱的局壓性能。任志剛等[9-10]主要研究圓端形鋼管混凝土短柱的極限承載力計(jì)算方法與偏壓截面優(yōu)化。但上述研究都缺少對(duì)該種柱強(qiáng)化方式的研究。王傳貽等[11]主要研究裝配式鋼骨-混凝土組合柱的抗震性能。尹朝正等[12]主要研究軸壓荷載作用下鋼骨混凝土組合短柱性能。周天華等[13]主要研究單軸對(duì)稱(chēng)十字型鋼中長(zhǎng)柱的偏壓性能，上述研究中對(duì)鋼骨混凝土的研究較為充分，同時(shí)也從側(cè)面證明了鋼骨混凝土具有良好使用性能，但現(xiàn)階段對(duì)鋼骨混凝土與圓端形鋼管混凝土相結(jié)合的研究較少。

考慮到鋼骨混凝土在相應(yīng)研究中表現(xiàn)出的實(shí)用性，現(xiàn)研究工字鋼強(qiáng)化圓端形鋼管混凝土短柱[14]方法的可行性，工字鋼參數(shù)變化對(duì)內(nèi)置工字鋼圓端形鋼管混凝土短柱局壓性能影響，并研究其相關(guān)性能。

1 有限元分析模型

1.1 有限元模型參數(shù)

內(nèi)置工字鋼圓端形鋼管混凝土短柱截面示意圖如圖1所示。將內(nèi)置工字鋼圓端形鋼管混凝土短柱分為縱向放置工字鋼和橫向放置工字鋼兩種情況進(jìn)行分析。

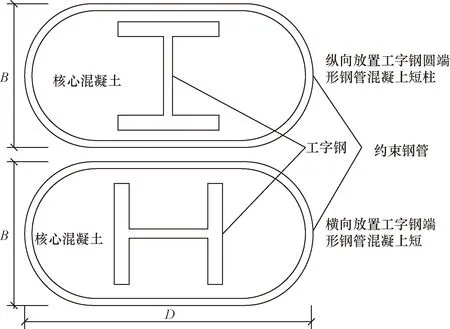
B為柱截面寬度；D為柱截面長(zhǎng)度圖1 內(nèi)置工字鋼圓端形鋼管混凝土短柱截面示意圖Fig.1 Section diagram of CECFST short column with built-in I-steel

建立的有限元模型參數(shù)表如表1所示。主要研究考慮工字鋼參數(shù)如下：工字鋼放置方向?yàn)榭v向放置工字鋼(ZG)和橫向放置工字鋼(HG)，工字鋼高度(GD)為25、50、75、100、125 mm，工字鋼寬度(KD)為25、50、75、100、125 mm，工字鋼翼緣厚度(YH)為10、15、20、25、30 mm，工字鋼腹板厚度(FH)為10、15、20、25、30 mm。

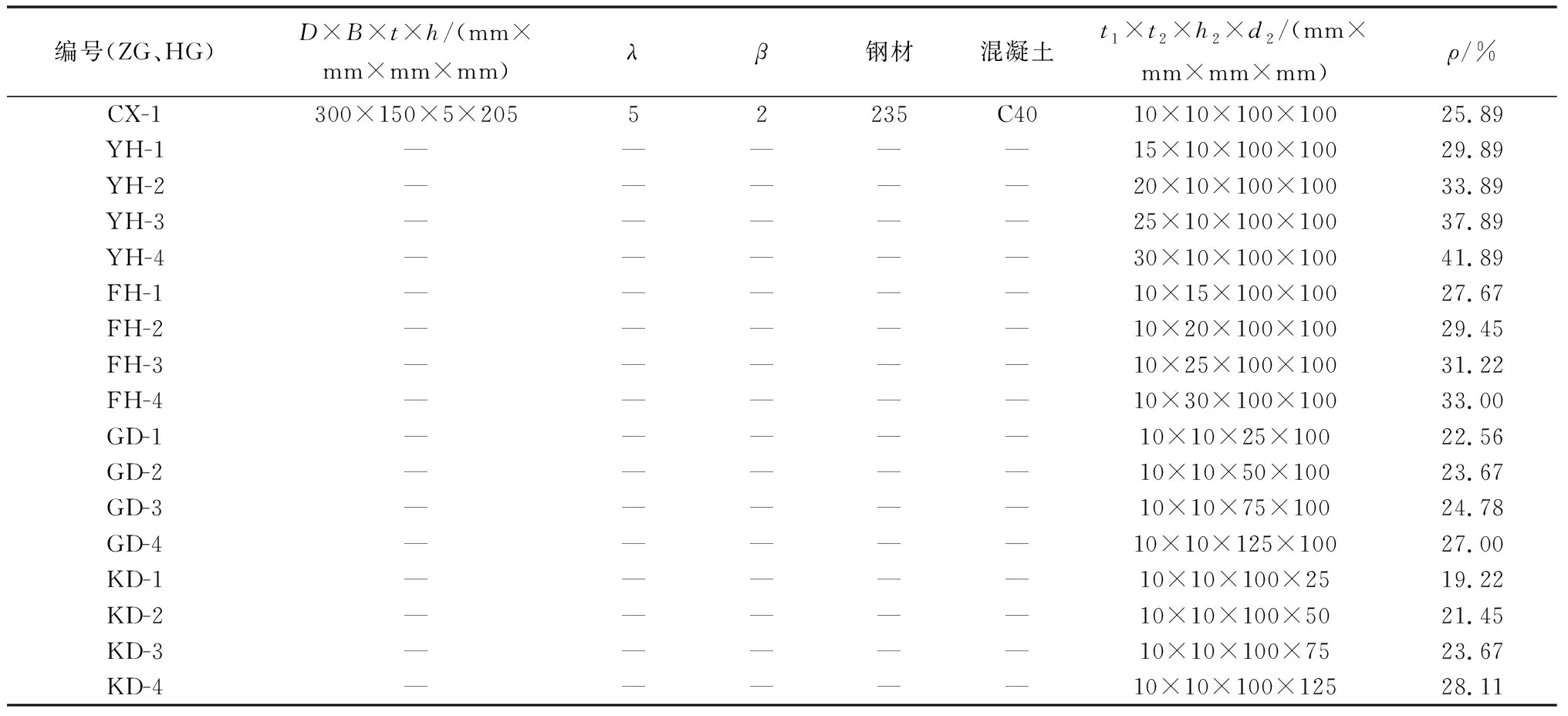
表1 有限元模型參數(shù)表Table 1 Parameters of finite element model

1.2 材料本構(gòu)模型及有限元模型建模過(guò)程

有限元模型涉及鋼材與混凝土，鋼材本構(gòu)關(guān)系使用二次塑流模型，其具體公式見(jiàn)文獻(xiàn)[15]。根據(jù)長(zhǎng)寬比β不同，將混凝土本構(gòu)關(guān)系分別等效為圓形與矩形鋼管混凝土柱混凝土本構(gòu)關(guān)系，其具體公式見(jiàn)文獻(xiàn)[16]。有限元模型各部分均采用C3D8R實(shí)體單元進(jìn)行建模，有限元模型及網(wǎng)格劃分示意圖如圖2所示。工字鋼單元格密度為7，混凝土單元格密度為13，鋼管單元格密度為17。

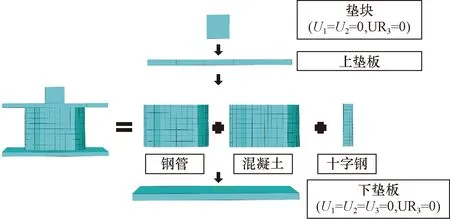
U1為X軸方向平移自由度；U2為Y軸方向平移自由度；U3為Z軸方向平移自由度；UR3為Z軸方向旋轉(zhuǎn)自由度圖2 有限元模型及網(wǎng)格劃分示意圖Fig.2 Schematic diagram of finite element model and meshing

混凝土與工字鋼、鋼管之間的接觸關(guān)系分別設(shè)定為法向、切向兩種行為，并各自設(shè)置為硬接觸、罰。根據(jù)文獻(xiàn)[16]，罰摩擦因數(shù)[17]設(shè)為0.3。柱底端采用鉸接約束，頂部采用固定滑輪約束，為實(shí)現(xiàn)局壓荷載作用，在柱頂端設(shè)置正方形墊塊，墊塊面積根據(jù)局壓面積比進(jìn)行設(shè)置，其具體計(jì)算公式見(jiàn)文獻(xiàn)[17]，局壓面積比(Г)設(shè)置為4。

1.3 有限元模型的驗(yàn)證

為驗(yàn)證有限元模型準(zhǔn)確，取文獻(xiàn)[18]圓端形鋼管混凝土短柱試驗(yàn)結(jié)果與有限元計(jì)算結(jié)果進(jìn)行比較，其對(duì)比結(jié)果如表2所示。N-μm曲線對(duì)比圖如圖3所示。N為施加于試件上的荷載，μm為對(duì)應(yīng)的位移值。

表2 文獻(xiàn)[18]試驗(yàn)結(jié)果與有限元結(jié)果對(duì)比表Table 2 Comparison of test results and finite element results in reference[18]

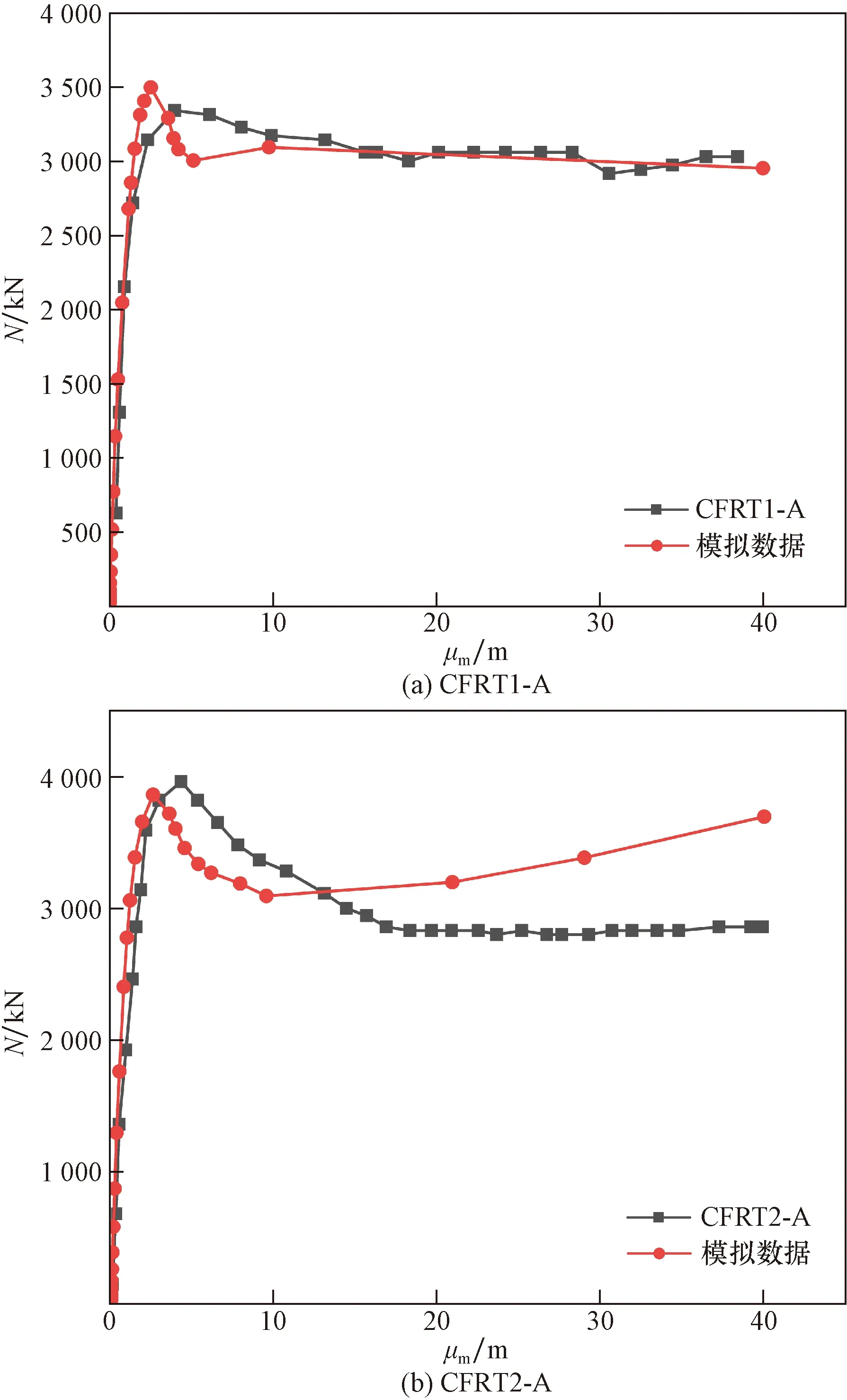
圖3 文獻(xiàn)[18]試驗(yàn)與有限元模型N-μm曲線對(duì)比Fig.3 Reference[18] test and finite element model N-μm curve comparison

結(jié)果表明，試驗(yàn)結(jié)果與有限元計(jì)算的N-μm曲線基本吻合，有限元計(jì)算承載力與試驗(yàn)承載力平均比值為1.03，可知有限元模型建立準(zhǔn)確。

2 參數(shù)分析

研究參數(shù)的N-μm曲線如圖4、圖5所示。

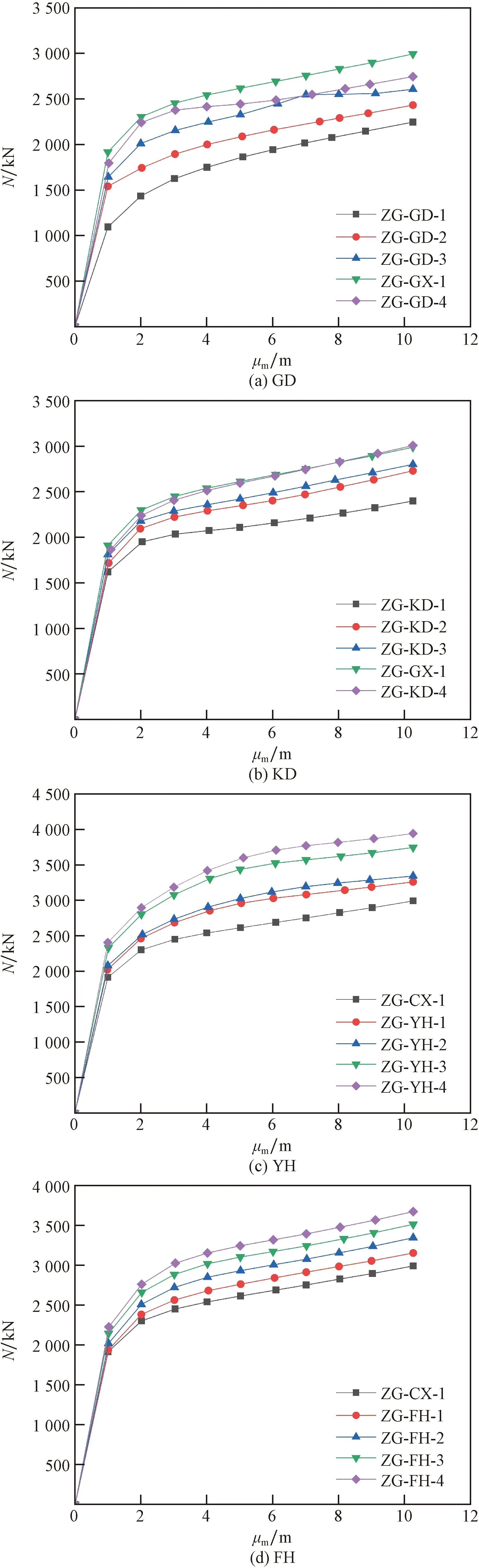
圖4 不同工字鋼參數(shù)下N-μm曲線(ZG)Fig.4 Different I-steel parameters N-μm curve (ZG)

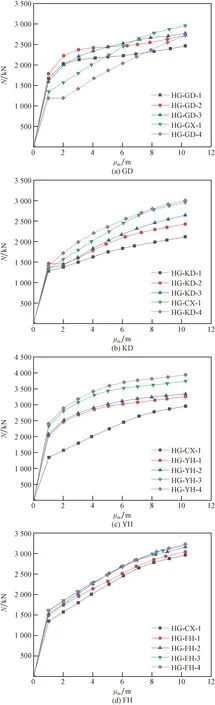
圖5 不同工字鋼參數(shù)下N-μm曲線(HG)Fig.5 Different I-steel parameters N-μm curve (HG)

2.1 工字鋼高度

由圖4(a)與圖5(a)分析可知，當(dāng)ZG時(shí)，承載力最高試件為ZG-CX-1，承載力為2 992 kN，承載力最低試件為ZG-GD-1，其承載力為2 244 kN。當(dāng)工字鋼高度由25 mm變?yōu)?0 mm時(shí)，承載力上升8.29%，由50 mm變?yōu)?5 mm時(shí)，承載力上升7.20%，由75 mm變?yōu)?00 mm時(shí)，承載力上升14.86%，由100 mm變?yōu)?25 mm時(shí)，承載力下降8.32%。

當(dāng)HG時(shí)，承載力最高試件為HG-CX-1，承載力為2 958 kN，承載力最低試件為HG-GD-1，承載力為2 465 kN。工字鋼高度由25 mm變?yōu)?0 mm時(shí)，承載力上升10.34%，由50 mm變?yōu)?5 mm時(shí)，承載力上升1.91%，由75 mm變?yōu)?00 mm時(shí)，承載力上升6.79%，由100 mm變?yōu)?25 mm時(shí)，承載力下降7.27%。

2.2 工字鋼寬度

由圖4(b)與圖5(b)分析可知，當(dāng)ZG時(shí)，承載力最高試件為ZG-KD-4，承載力為3 011 kN，承載力最低試件為ZG-KD-1，承載力為2 402 kN。工字鋼寬度由25 mm變?yōu)?0 mm時(shí)，承載力上升13.78%，由50 mm變?yōu)?5 mm時(shí)，承載力上升2.56%，由75 mm變?yōu)?00 mm時(shí)，承載力上升6.74%，由100 mm變?yōu)?25 mm時(shí)，承載力上升0.64%。

當(dāng)HG時(shí)，承載力最高試件為HG-KD-4，承載力為3 006 kN，承載力最低試件為HG-KD-1，承載力為2 119 kN。工字鋼寬度由25 mm變?yōu)?0 mm時(shí)，承載力上升14.58%，由50 mm變?yōu)?5 mm時(shí)，其承載力上升8.98%，由75 mm變?yōu)?00 mm時(shí)，其承載力上升11.79%，由100 mm變?yōu)?25 mm時(shí)，其承載力上升1.62%。

2.3 工字鋼翼緣厚度

由圖4(c)與圖5(c)分析可知，當(dāng)ZG時(shí)，承載力最高試件為ZG-YH-4，承載力為3 943 kN，承載力最低試件為ZG-CX-1，承載力為2 992 kN。工字鋼翼緣由10 mm變?yōu)?5 mm時(shí)，承載力上升8.96%，由15 mm變?yōu)?0 mm時(shí)，承載力上升2.55%，由20 mm變?yōu)?5 mm時(shí)，承載力上升12.03%，由25 mm變?yōu)?0 mm時(shí)，承載力上升5.29%。

當(dāng)HG時(shí)，承載力最高試件為HG-YH-4，承載力為4 163 kN，承載力最低試件為HG-CX-1，承載力為2 958 kN。工字鋼翼緣由10 mm變?yōu)?5 mm時(shí)，承載力上升15.55%，由15 mm變?yōu)?0 mm時(shí)，承載力上升4.45%，由20 mm變?yōu)?5 mm時(shí)，承載力上升10.31%，由25 mm變?yōu)?0 mm時(shí)，承載力上升5.71%。

2.4 工字鋼腹板厚度

由圖4(d)與圖5(d)分析可知，當(dāng)ZG時(shí)，承載力最高試件為ZG-FH-4，承載力為3 673 kN，承載力最低試件為ZG-CX-1，承載力為2 992 kN。工字鋼腹板由10 mm變?yōu)?5 mm時(shí)，承載力上升5.41%，由15 mm變?yōu)?0 mm時(shí)，承載力上升6.06%，由20 mm變?yōu)?5 mm時(shí)，承載力上升5.05%，由25 mm變?yōu)?0 mm時(shí)，承載力上升4.52%。

當(dāng)HG時(shí)，承載力最高試件為HG-FH-4，承載力為3 227 kN，承載力最低試件為HG-CX-1，承載力為2 958 kN。工字鋼腹板由10 mm變?yōu)?5 mm時(shí)，其承載力上升2.67%，由15 mm變?yōu)?0 mm時(shí)，承載力上升3.89%，由20 mm變?yōu)?5 mm時(shí)，承載力上升1.43%，由25 mm變?yōu)?0 mm時(shí)，承載力上升0.84%。

模擬過(guò)程中，當(dāng)工字鋼高度超過(guò)100 mm時(shí)，承載力出現(xiàn)下降，且HG與ZG兩種情況皆出現(xiàn)該種情況，分析其原因?yàn)椋?dāng)工字鋼高度超過(guò)100 mm后，工字鋼翼緣部分完全脫離局壓加載區(qū)域，在這種情況下，翼緣部分不能完全承受外力作用，其示意圖如圖6所示。

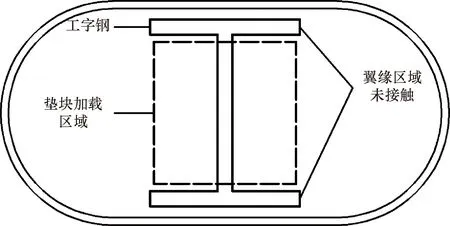
圖6 工字鋼高度超過(guò)100 mm承載力下降情況示意圖Fig.6 Schematic diagram of bearing capacity decline of I-steel with height exceeding 100 mm

2.5 工字鋼放置方向?qū)Ρ?/h3>

以ρ為基準(zhǔn)對(duì)比不同工字鋼參數(shù)對(duì)局壓承載力的影響，并對(duì)比出該種情況下對(duì)承載力影響較大的參數(shù)，曲線如圖7所示。

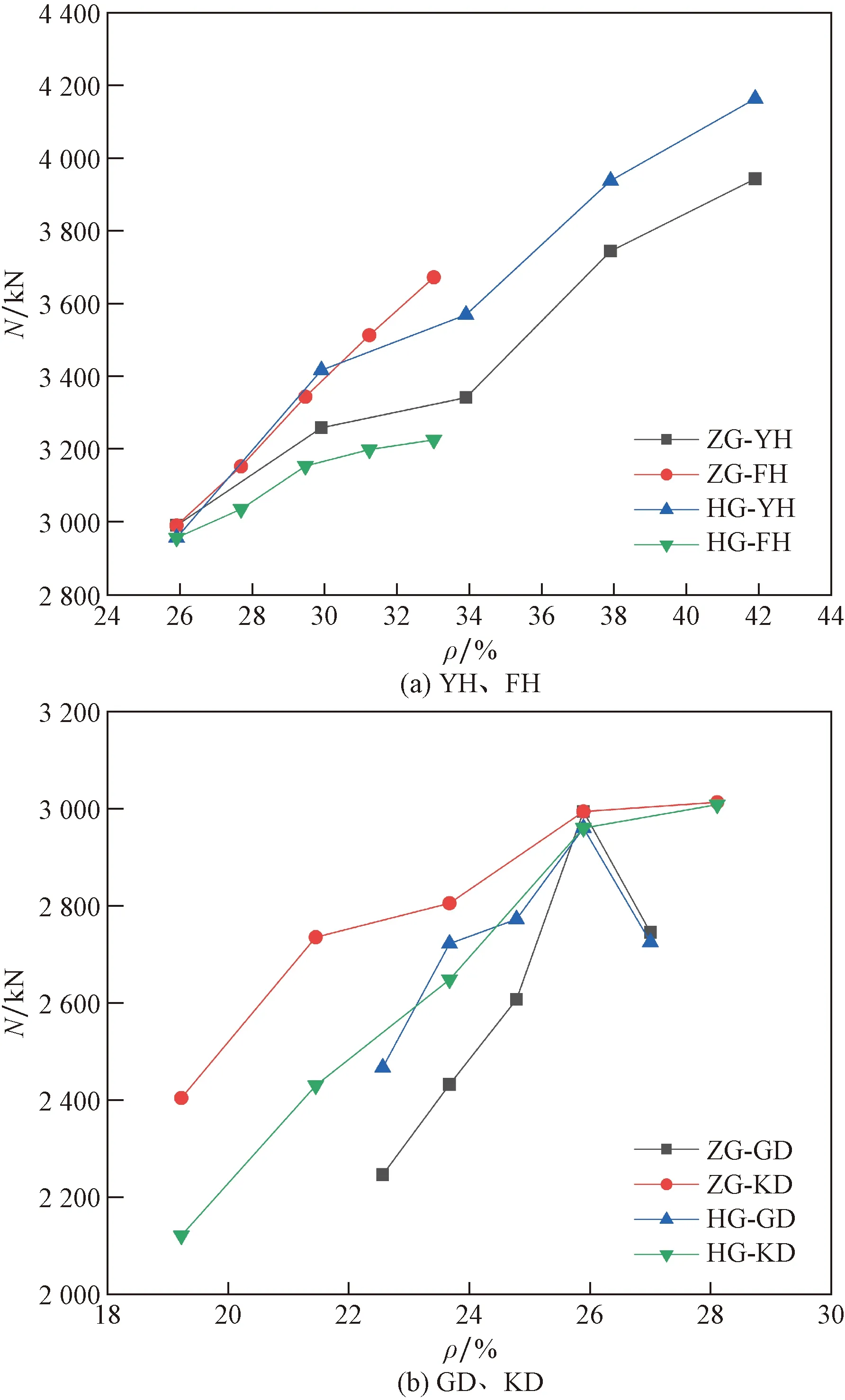
圖7 不同ρ圓端形鋼管混凝土短柱承載力對(duì)比圖Fig.7 Performance comparison diagram of different ρ of CECFST

由圖7(a)分析可知，對(duì)比工字鋼翼緣厚度與腹板厚度參數(shù)變化對(duì)局壓承載力的影響，當(dāng)ρ<34%時(shí)，ZG-FH參數(shù)變化對(duì)局壓承載力影響較大。當(dāng)ρ>34%時(shí)，HG-YH參數(shù)變化對(duì)局壓承載力影響較大。

由圖7(b)分析可知，對(duì)比工字鋼高度與工字鋼寬度參數(shù)變化對(duì)局壓承載力的影響，ZG-KD參數(shù)變化對(duì)局壓承載力強(qiáng)化較大。

3 破壞模態(tài)分析

通過(guò)對(duì)試件ZG-CX-1的應(yīng)力云圖進(jìn)行分析，得出該種情況下柱的破壞模態(tài)，應(yīng)力云圖如圖8所示。

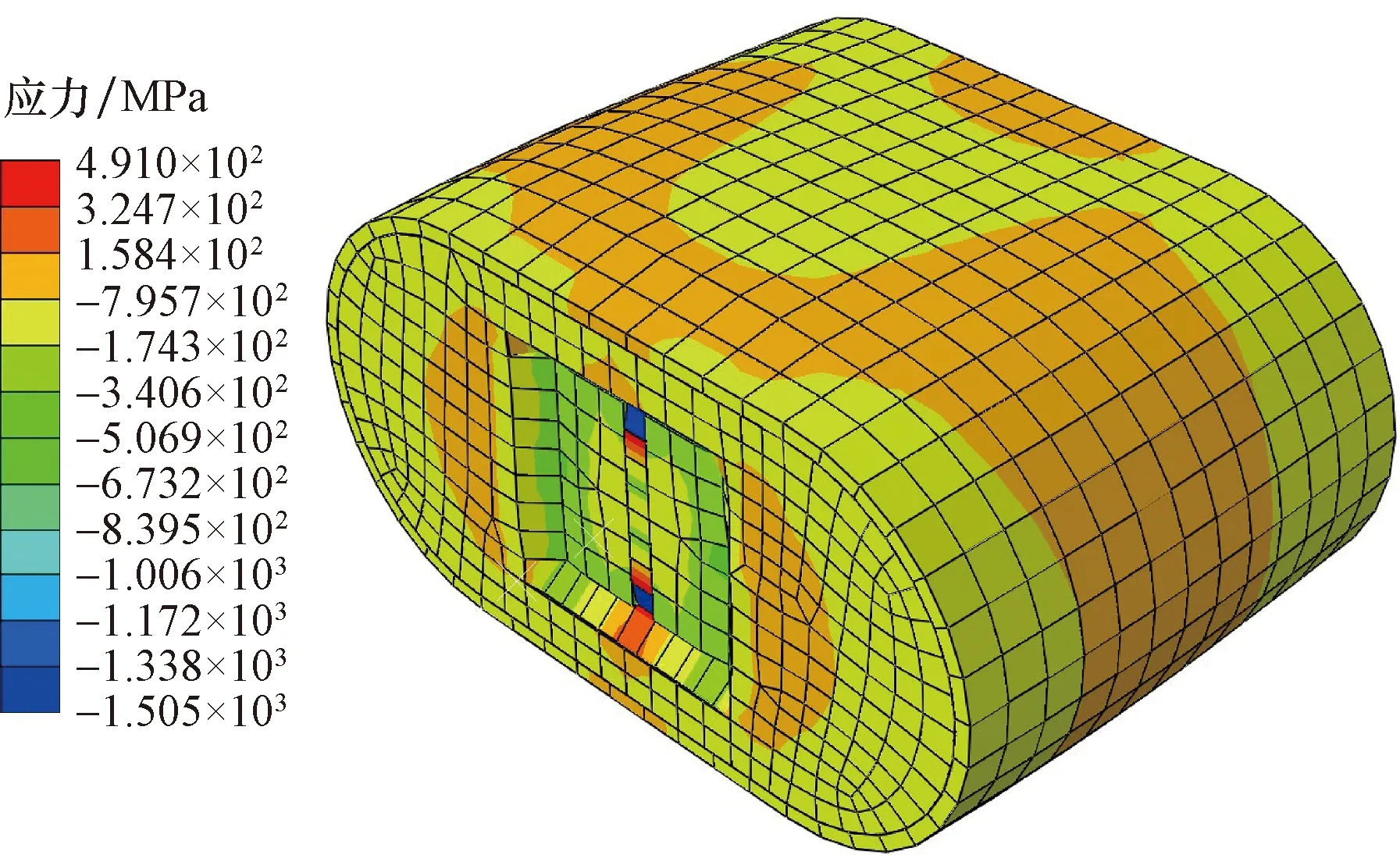
圖8 局壓荷載作用下圓端形鋼管混凝土短柱破壞模態(tài) Fig.8 Failure modes of CECFST short columns under local compressive load

由圖8可知，局壓荷載作用下圓端形鋼管混凝土短柱破壞模態(tài)主要表現(xiàn)為：墊塊加載位置混凝土出現(xiàn)凹陷；在墊塊加載位置外的混凝土，因局壓荷載作用而與鋼管發(fā)生脫離。外鋼管加載端部凸起，且其加載端縱向位置鋼管凸起最為嚴(yán)重。

4 局壓承載力計(jì)算公式

內(nèi)置工字鋼圓端形鋼管混凝土短柱局壓承載力計(jì)算公式參考文獻(xiàn)如下：①文獻(xiàn)[8]，研究的圓端形橢圓鋼管混凝土短柱承載力計(jì)算公式；②文獻(xiàn)[16]，研究的圓端形橢圓鋼管混凝土的軸壓性能；③文獻(xiàn)[19]和文獻(xiàn)[20]，對(duì)內(nèi)置型鋼的鋼管混凝土柱承載力計(jì)算公式的研究。

同時(shí)，在上述研究基礎(chǔ)上，考慮內(nèi)置型鋼、工字鋼放置方向及工字鋼高度對(duì)局壓承載力的影響，其具體公式為

(1)

式(1)中：Njy為內(nèi)置工字鋼圓端形鋼管混凝土短柱局壓承載力；Klc為局壓折減系數(shù)；Nu為內(nèi)置工字鋼圓端形鋼管混凝土短柱承載力；Cdir為工字鋼放置方向影響系數(shù)；Chig為工字鋼高度影響系數(shù)。

Klc=(A3Γ+B3Γ0.5+C3)/f(β)

(2)

式(2)中：A3、B3、C3、f(β)分別為局壓折減系數(shù)計(jì)算系數(shù)1、2、3、4。

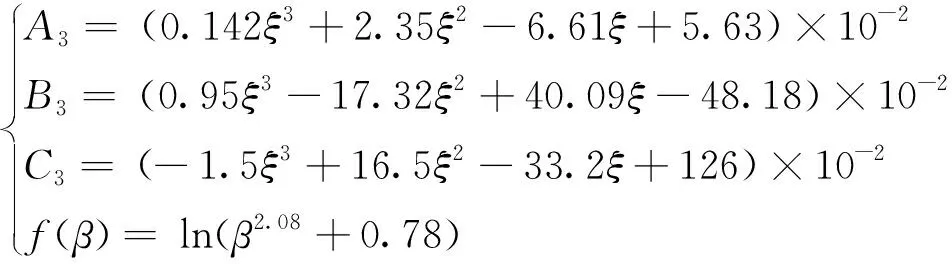
(3)

式(3)中：ξ為圓端形橢圓鋼管混凝土約束效應(yīng)系數(shù)。

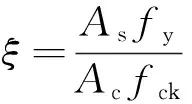
(4)

式(4)中：As為圓端形鋼管截面面積；fy為鋼管屈服強(qiáng)度；Ac為混凝土截面面積；fck為混凝土軸心抗壓強(qiáng)度標(biāo)準(zhǔn)值。

Nu=Ascfscy+Agsfgsd

(5)

式(5)中：Asc為圓端形鋼管混凝土短柱全截面面積；fscy為圓端形鋼管混凝土短柱統(tǒng)一強(qiáng)度；Ags為工字鋼截面面積；fgsd為工字鋼屈服強(qiáng)度。

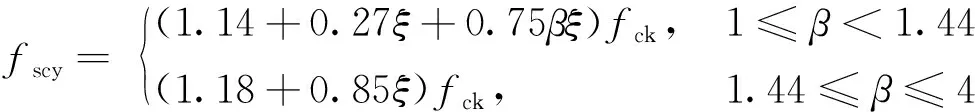
(6)

通過(guò)所提出的局壓承載力公式計(jì)算承載力與模擬結(jié)果對(duì)比結(jié)果如表3所示。

由表3對(duì)比結(jié)果可知，本文公式計(jì)算承載力與模擬承載力比值區(qū)間為0.86～1.06，誤差小于10%，計(jì)算結(jié)果較準(zhǔn)確，可以應(yīng)用于承載力計(jì)算。

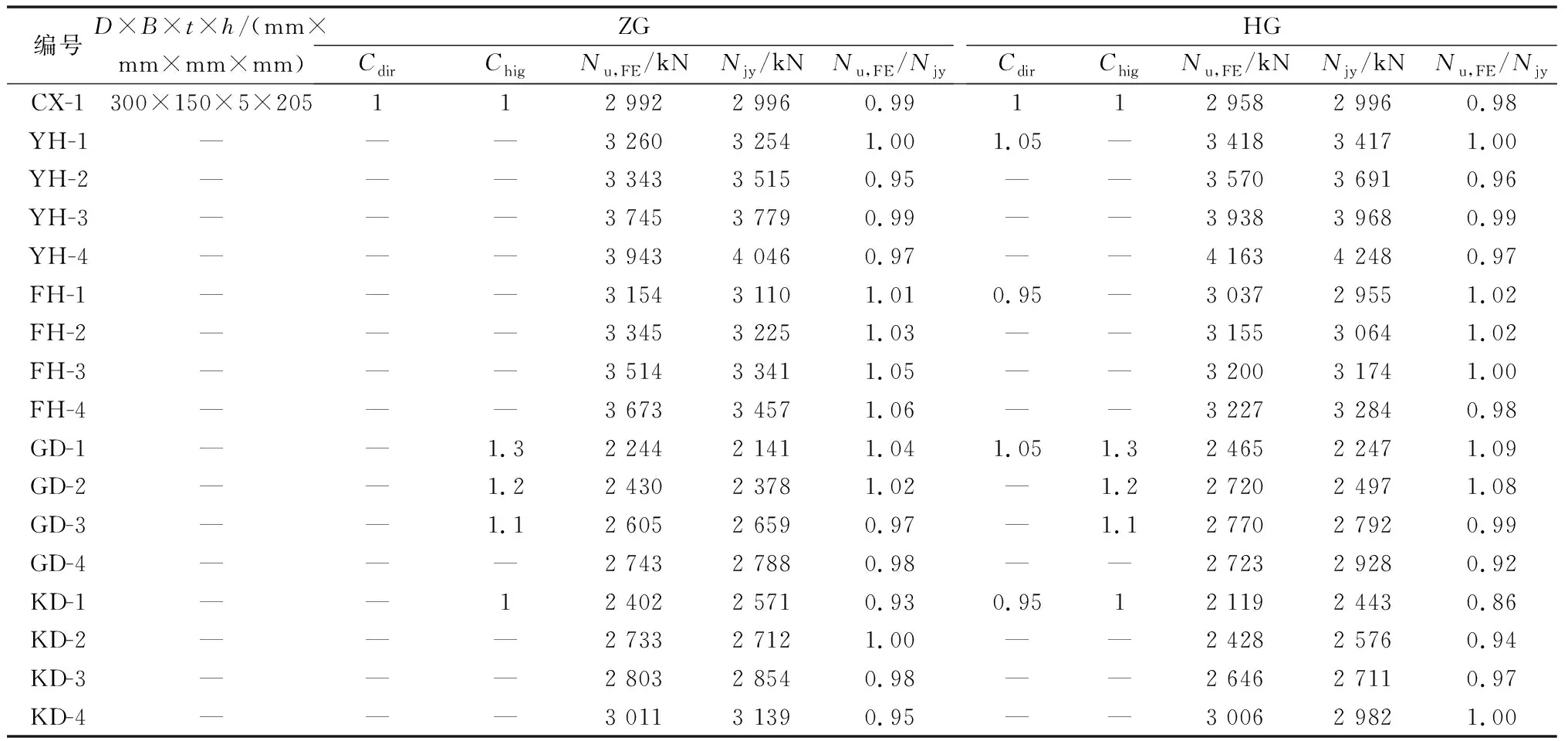
表3 模擬承載力、計(jì)算承載力對(duì)比表Table 3 Comparison of simulated bearing capacity and calculated bearing capacity

5 結(jié)論

(1)當(dāng)ρ<34%時(shí)，ZG-FH參數(shù)變化對(duì)局壓承載力影響較大；當(dāng)ρ>34%時(shí)，HG-YH參數(shù)變化對(duì)局壓承載力影響較大。對(duì)比工字鋼高度與工字鋼寬度變化對(duì)局壓承載力的影響，ZG-KD參數(shù)變化對(duì)局壓承載力影響較大。

(2)使用工字鋼強(qiáng)化圓端形鋼管混凝土短柱局壓性能時(shí)，若工字鋼超出墊塊加載位置，承載力下降，分析其原因?yàn)椋瑢?duì)局壓性能的強(qiáng)化中，對(duì)加載區(qū)域進(jìn)行強(qiáng)化的效果明顯強(qiáng)于對(duì)加載區(qū)域外進(jìn)行強(qiáng)化。

(3)局壓荷載作用下圓端形鋼管混凝土短柱破壞模態(tài)為，墊塊加載位置混凝土凹陷，墊塊加載位置外混凝土與鋼管發(fā)生脫離，外鋼管加載端縱向位置鋼管凸起嚴(yán)重，加載位置工字鋼變形嚴(yán)重。

(4)根據(jù)前人研究提出內(nèi)置工字鋼圓端形鋼管混凝土短柱局壓承載力計(jì)算公式，并使用所提公式與模擬結(jié)果進(jìn)行驗(yàn)證，所提公式計(jì)算承載力與模擬承載力比值為0.86～1.06，誤差小于10%，計(jì)算結(jié)果較為準(zhǔn)確，可以用于承載力計(jì)算，并為相關(guān)的研究提供依據(jù)。