淺談函數(shù)中如何尋找同構(gòu)解決“指對”問題
——2022年新高考Ⅰ卷第22題帶來的思考
劉明明
?江蘇省南通市如東高級中學(xué)
全國高考數(shù)學(xué)卷中經(jīng)常出現(xiàn)構(gòu)造同構(gòu)函數(shù)解決與函數(shù)有關(guān)的問題,尤其在處理“指對”問題時(shí),通過同構(gòu)函數(shù)往往能更好更快捷地解決問題.下面從2022年新高考Ⅰ卷第22題第(2)問出發(fā),探索同構(gòu)函數(shù)在解決“指對”問題中的應(yīng)用.
1 原題呈現(xiàn)及分析
證明:存在直線y=b,其與兩條曲線f(x)=ex-x,g(x)=x-lnx共有三個(gè)不同的交點(diǎn),并且從左到右的三個(gè)交點(diǎn)的橫坐標(biāo)成等差數(shù)列.
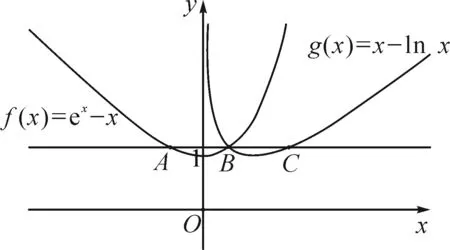
圖1
分析:給出直線y=b,及兩條曲線f(x)=ex-x,g(x)=x-lnx的圖象,如圖1所示.
不妨設(shè)三個(gè)交點(diǎn)的橫坐標(biāo)從左到右依次為x1,x2,x3,則有x1<0 由ex1-x1=eln x2-lnx2,知f(x1)=f(lnx2),又x1<0,lnx2<0,f(x)=ex-x在(-∞,0)上單調(diào)遞減,故x1=lnx2;由ex2-x2=eln x3-lnx3,知f(x2)=f(lnx3),又x2>0,lnx3>0,f(x)=ex-x在(0,+∞)上單調(diào)遞增,故x2=lnx3. 所以x1+x3=ex1+lnx3=eln x2+x2=2x2,原命題得證. 從上述分析可以看到,通過公式alogaN=N(N>0),logaaN=N(a>0,且a≠1),尋找方程中的相同結(jié)構(gòu),并利用函數(shù)f(x)=ex-x在(-∞,0),(0,+∞)的單調(diào)性,將復(fù)雜的“指對”等量關(guān)系式轉(zhuǎn)化為簡單的關(guān)于自變量的等量關(guān)系式.同時(shí),我們不禁有這樣一些思考:我們平時(shí)遇到的“指對”問題,是否同樣可以通過同構(gòu)函數(shù)加以解決?若能,則在“指對”問題中怎樣才能找到同構(gòu)函數(shù)呢?筆者通過以下幾個(gè)方面來揭示運(yùn)用“同構(gòu)”思想處理“指對”問題的思維過程. 例1(2020年新課標(biāo)Ⅱ卷第12題)若2x-2y<3-x-3-y,則( ). A.ln(y-x+1)>0 B.ln(y-x+1)<0 C.ln|x-y|>0 D.ln|x-y|<0 解:由2x-2y<3-x-3-y移項(xiàng)變形為2x-3-x<2y-3-y.令f(x)=2x-3-x,則原不等式即為f(x) 例1主要揭示了同構(gòu)函數(shù)法不僅能應(yīng)用于方程問題中,在不等式問題中也有廣泛的運(yùn)用,通過移項(xiàng)變形在等號(或不等號)兩邊分別構(gòu)造同構(gòu)形式,從而幫助我們更快捷地解決方程或不等式問題.如果遇到較復(fù)雜的含參恒成立問題呢?如例2. 例2(2020年新課標(biāo)山東卷)已知函數(shù)f(x)=aex-1-lnx+lna.若f(x)≥1,求a的取值范圍. 解法1:利用指數(shù)對數(shù)的運(yùn)算可將f(x)=aex-1-lnx+lna=eln a+x-1-lnx+lna≥1等價(jià)轉(zhuǎn)化為 eln a+x-1+lna+x-1≥lnx+x=eln x+lnx. ① 令g(x)=ex+x,則不等式①可等價(jià)轉(zhuǎn)化為g(lna+x-1)≥g(lnx).顯然g(x)為單調(diào)增函數(shù),則不等式①進(jìn)一步等價(jià)轉(zhuǎn)化為lna≥lnx-x+1. 令h(x)=lnx-x+1,利用導(dǎo)數(shù)求得h(x)max=h(1)=0,則lna≥0,即a≥1. 所以a的取值范圍為[1,+∞). 在例2的同構(gòu)轉(zhuǎn)化過程中,恒成立問題中的參數(shù)盡量放在同一函數(shù)的不同位置或不同函數(shù)的相同位置.當(dāng)然例2的轉(zhuǎn)化并不唯一,還可以如下處理. 所以a的取值范圍為[1,+∞). 通過解法1與解法2可以看到為解決問題構(gòu)造的同構(gòu)函數(shù)并不唯一,而且例2還可以構(gòu)造y=xlnx,y=x+lnx等同構(gòu)函數(shù)來解決問題.但對比這些不同的同構(gòu)函數(shù),我們發(fā)現(xiàn)利用g(x)=ex+x處理問題更簡潔方便,主要原因是相對于其他同構(gòu)函數(shù),g(x)的單調(diào)區(qū)間(-∞,+∞)最長,這樣就不必對自變量是否在單調(diào)區(qū)間內(nèi)加以討論,故構(gòu)造同構(gòu)函數(shù)解決問題時(shí),我們應(yīng)盡量選擇單調(diào)區(qū)間較長的函數(shù). 例3(2020年新課標(biāo)Ⅰ卷第12題)若2a+log2a=4b+2log4b,則( ). A.a>2bB.a<2b C.a>b2D.a 解:因?yàn)?b+2log4b=22b+log2(2b)-1,所以2a+log2a=22b+log2(2b)-1. 于是2a+log2a<22b+log2(2b). 設(shè)f(x)=2x+log2x,則有f(a) 對于例3,主要是利用放縮法將方程轉(zhuǎn)化為兩邊可以構(gòu)造同構(gòu)函數(shù)的不等式形式,再由同構(gòu)函數(shù)的單調(diào)性判斷自變量的大小.類似的方法在證明含參不等式中也有著廣泛的應(yīng)用,如以下例4. ② 故當(dāng)ln(ex)≤0時(shí),②式顯然成立.當(dāng)ln(ex)≥0時(shí),令g(x)=xex.由g′(x)=ex(x+1),知g(x)在(0,+∞)上增函數(shù),又易證x≥ln(ex)=lnx+1,所以g(x)≥g(ln(ex)),即xex≥eln(ex)ln(ex)成立,亦即②式成立. 上述例3與例4都采用了放縮法尋找不等式兩邊的同構(gòu)形式.有些問題中還可以利用一些常見不等式(如ex≥x+1)進(jìn)行放縮,比如例5. 例5已知函數(shù)f(x)=x(e2x-a),若x>0時(shí),f(x)≥1+x+lnx恒成立,求實(shí)數(shù)a的取值范圍. 例5通過e2x+ln x≥2x+lnx+1的放縮,達(dá)成了分式的分子分母同構(gòu),巧妙得到不等式右邊的最小值,極大地優(yōu)化了本題的解題步驟. 這些類同構(gòu)問題的解決過程也告訴我們:在平時(shí)的解題中,不能思維僵化,要多從范圍、常見不等式等角度思考可否化為同構(gòu)問題解決. 易知g(t)≥g(e2)=e2-2e2+e2=0.又0 所以0 例7(2013年新課標(biāo)Ⅱ卷)已知函數(shù)f(x)=ex-ln(x+m),當(dāng)m≤2時(shí),證明f(x)>0. 證明:令g(x)=ex-x-1,則要證f(x)>0成立,即證g(x)+g(ln(x+m))+2-m>0成立. 又g(x)≥0,g(ln(x+m))≥0,當(dāng)且僅當(dāng)x=0且m=1時(shí),上述兩個(gè)不等式的等號同時(shí)成立.又m≤2,所以2-m≥0,當(dāng)m=2時(shí),等號成立.即上述3個(gè)等號不能同時(shí)取到.于是f(x)>0. 故原命題得證. 例7中的局部同構(gòu)與例6有所不同,它尋找的不是自變量的局部同構(gòu),而是通過常用母函數(shù)f(x)=ex-x-1尋找整個(gè)函數(shù)的局部同構(gòu)(形如f(x1)+f(x2)+m).這里如果先對例7的參數(shù)進(jìn)行放縮,會更容易尋找到例7的局部同構(gòu).如以下另一角度. 另一角度:令g(x)=ex-x-1,要證m≤2時(shí),f(x)>0,只需證ex-ln(x+2)>0,即證g(x)+g(ln(x+2))>0.又由g(x)≥0,g(ln(x+2))≥0,當(dāng)且僅當(dāng)x=0且x=-1時(shí),兩個(gè)等號同時(shí)成立.又等號取不到,故原命題得證. 從以上的思考角度我們可以看到,這三種類型同構(gòu)問題并不是孤立的,而是相互聯(lián)系的,在解決“指對”問題時(shí)需要靈活加以運(yùn)用. 最后,大數(shù)據(jù)顯示“指對”問題在全國卷中的出現(xiàn)非常頻繁,而構(gòu)造同構(gòu)函數(shù)的思想在解決“指對”問題時(shí)也越來越重要,因此在平時(shí)的教學(xué)中要向?qū)W生多滲透,讓他們在解決“指對”問題時(shí)更加游刃有余.2 “同構(gòu)”思想處理“指對”問題的思維過程
2.1 在等號(或不等號)兩邊分別構(gòu)造同構(gòu)函數(shù)
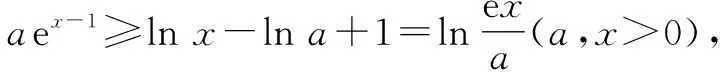
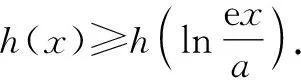
2.2 利用放縮構(gòu)造不等式中的同構(gòu)函數(shù)
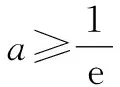
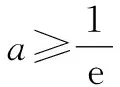
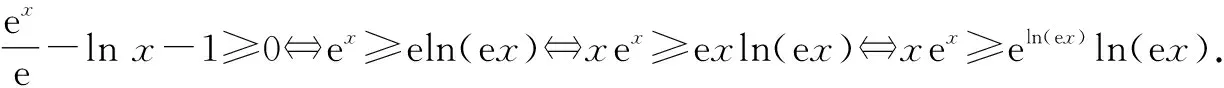
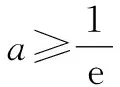
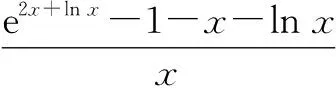
2.3尋找方程、不等式中的局部同構(gòu)