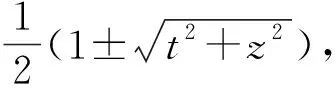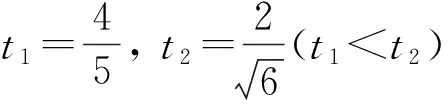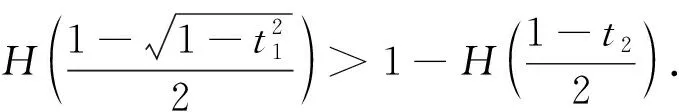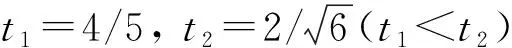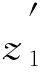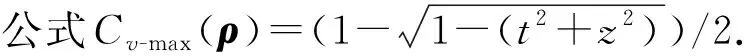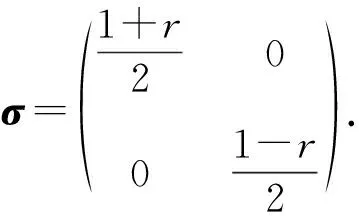單量子系統中基于相干度量的態排序

胡曉會, 玄東平, 南 華

(延邊大學 理學院, 吉林 延吉 133002)

量子相干性在低溫熱力學、量子生物學和納米物理學等領域應用廣泛.文獻[1]提出了量化相干資源理論框架；文獻[2]提出了另一個量化相干框架.在量子信息處理進程中存在不同相干度量, 如l1-范數相干度量、相對熵相干度量和魯棒相干度量等.與量子糾纏類似, 不同的量子相干度量可表征不同量子態, 一個給定的量子態可能在一次信息處理中表現較好, 但在其他信息處理中該量子態的適用性可能相對較差.若2個糾纏度量對純態有相同排序, 則任意2個態就會有相同排序, 從而純態中存在的排序關系即可延拓至任意的量子態[3].若2個相干度量對所有量子態有相同排序, 則可在某種程度上識別它們.由于不同的相干度量有不同排序, 因此在不同的量子相干度量下如何對量子態進行排序已引起人們廣泛關注[4].

文獻[5-7]研究了l1-范數相干度量、相對熵相干度量以及α親和相干度量的量子態排序關系；文獻[8]研究了Tsallis-α相對熵相干度量的量子態排序.本文基于相對熵相干度量、斜信息相干度量和Hellinger距離相干度量等研究單量子系統中的態排序.

1 幾種相干度量和態排序

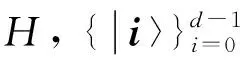
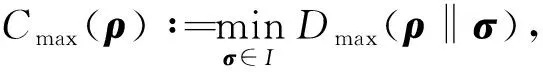
(1)

其中Dmax(ρ‖σ)=min{λ:ρ≤2λσ}是量子態ρ相對于量子態σ的最大相對熵.

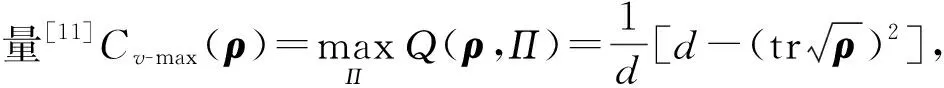
定義1[6]設CA和CB是2個相干度量, 對于Hilbert空間H中任意2個態ρ1和ρ2, 若

CA(ρ1)≤CA(ρ2) ?CB(ρ1)≤CB(ρ2),

則稱CA和CB提供相同的態排序.否則, 稱這2個度量不能提供相同的態排序.

由于C(ρ)是一個非負實數, 因此根據不同相干度量, 所有的態總可以進行排序.

2 基于相干度量的純態排序

根據不同相干度量研究純態的單量子比特系統中態排序問題.

結論1對于單量子比特系統中的純態, 相對熵相干度量Cr、斜信息相干度CI以及Hellinger距離相干度量CH提供相同的態排序.

證明： 單量子系統中任意量子態設為

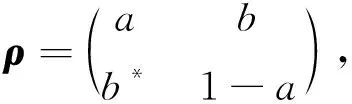
(2)

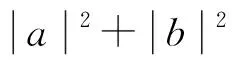
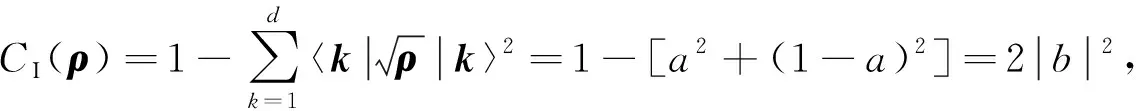
(3)

以及Hellinger距離相干度量

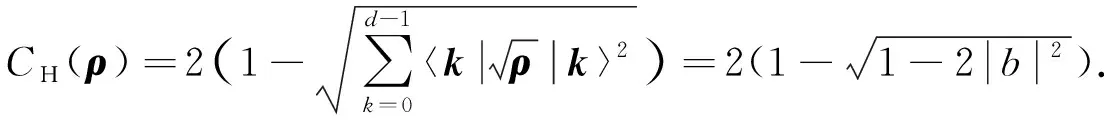
(4)

由式(3)和式(4)可知,CI(ρ)和CH(ρ)均為關于|b|的增函數, 因此相干度量CI(ρ)和CH(ρ)具有相同的態排序.即對任意2個純態ρ1和ρ2, 有CI(ρ1)≤CI(ρ2)?|b1|≤|b2|?CH(ρ1)≤CH(ρ2).

任意的單量子比特態ρ通常還可表示為

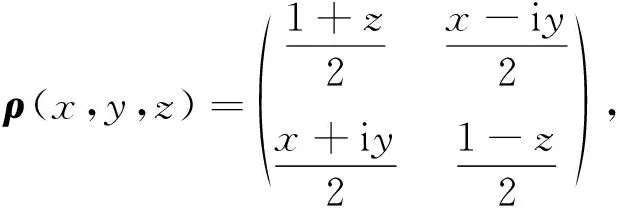
(5)

其中x2+y2+z2≤1(純態時等號成立).令

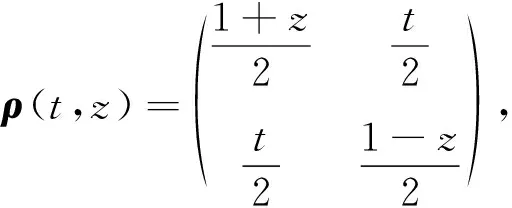
(6)

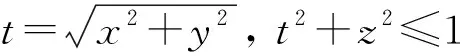
例1考慮如下2個單量子比特純態:

通過計算可得

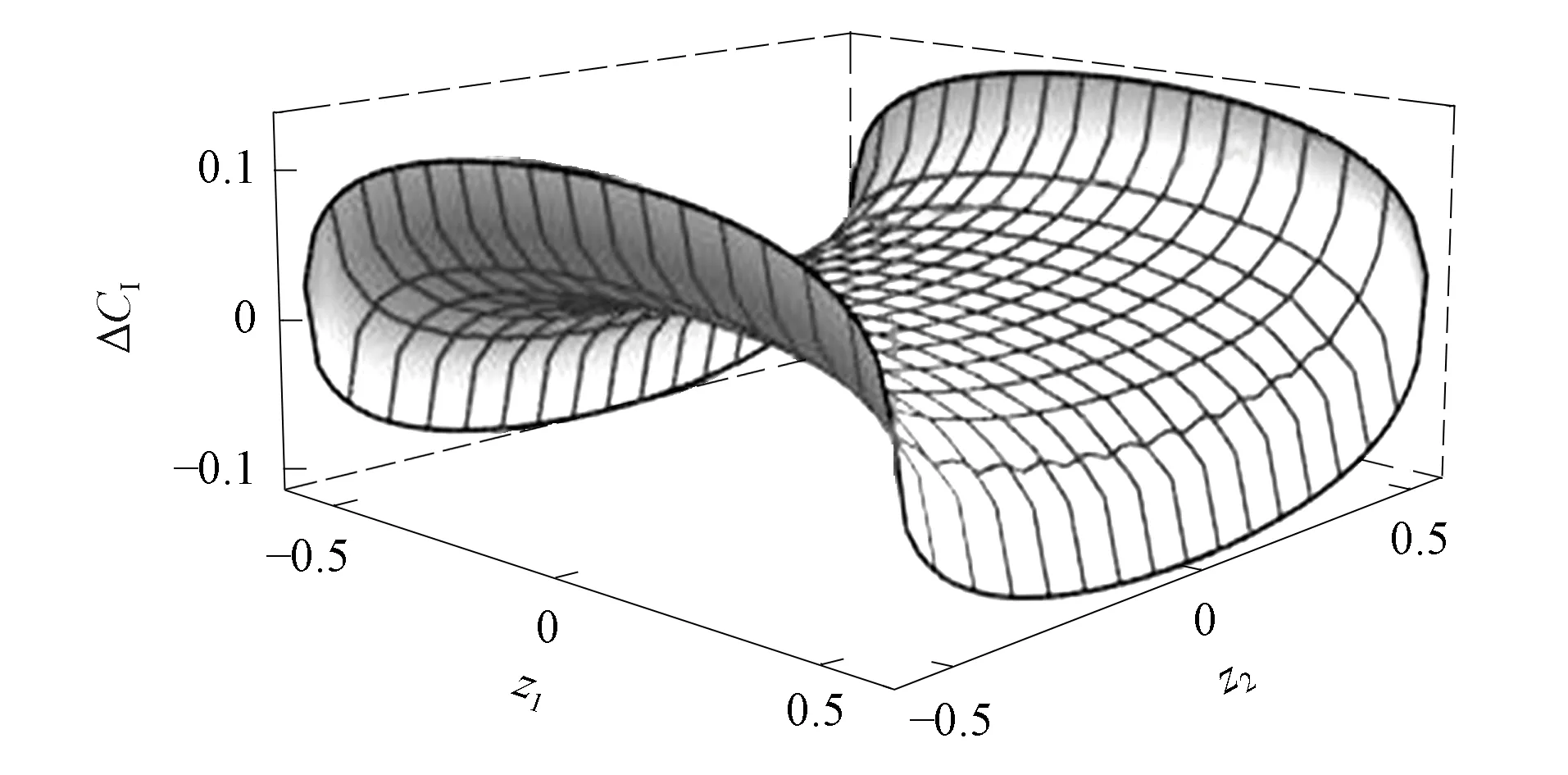
Cr(σ1)=0.721 9

CH(σ1)=0.350 8

從而驗證了上述相干度量提供相同的態排序.

例2考慮如下2個單量子比特混合態:

由定義可得

Cr(σ1)=0.627 1>Cr(σ2)=0.533 8,CI(σ1)=0.241 0>CI(σ2)=0.201 2,

CH(σ1)=0.257 6>CH(σ2)=0.212 5.

3 基于相干度量的混合態排序

下面討論混合態Cr,CI,CH的態排序問題.根據CI(ρ)和CH(ρ)的定義解析表達式可知, 由于CI(ρ)和CH(ρ)對任意態提供相同的態排序, 因此僅需討論Cr(ρ)和CI(ρ)的態排序,Cr(ρ)和CH(ρ)必有類似的結果.

圖1 當時, ΔCI的三維圖像Fig.1 Three-dimensional image of ΔCI when t1=4/5,

(7)

結論2對單量子比特系統中的混合態,Cr和CI及Cr和CH不能提供相同的態排序.

例3對單量子系統中的2個量子態:

可直接計算求得基于不同度量的相干性：

CI(σ1)=0.32>CI(σ2)=0.304 0,CH(σ1)=0.350 8>CH(σ2)=0.331 5,

Cr(σ1)=0.721 9

例2中Cr(ρ)和CI(ρ)及Cr(ρ)和CH(ρ)同序, 但在這里是反序, 因此Cr和CI及Cr和CH不能提供相同的態排序.

結論3對單量子比特系統中的混合態,Cv-max(ρ)和Cr(ρ),Cv-max(ρ)和CI(ρ)及Cv-max(ρ)和CH(ρ)均不能提供相同的態排序.

例4對如下3個混合態:

Cv-max(σ1)=0.334 9>Cv-max(σ2)=0.201 2

(8)

CI(σ1)=0.241 0>CI(σ2)=0.201 2

(9)

Cr(σ1)=0.627 1>Cr(σ2)=0.533 8

(10)

式(8)～(10)中至少有一個不等號方向不一致, 表明Cv-max(ρ)和Cr(ρ),Cv-max(ρ)和CI(ρ)及Cv-max(ρ)和CH(ρ)均不能提供相同的態排序.

結論4對單量子比特系統態(純態或混合態), 最大相對熵相干度量Cmax(ρ)與l1-范數相干度Cl1提供相同的態排序.

由此可得Cmax(ρ)與其他相干度量的態排序關系.

綜上, 本文研究了在單量子比特系統中基于幾個相干度量的態排序問題, 并討論了Cv-max(ρ)以及Cmax(ρ)與其他相干度量的態排序問題.結果表明：l1-范數相干度量、相對熵相干度量、斜信息相干度量及Hellinger距離相干度量對純態提供相同的態排序, 對混合態則不能提供相同的態排序, 并給出了例證; 基于von Neumann測量的最大相干度量、相對熵相干度量及斜信息相干度量對混合態也不能提供相同態排序.