中間特征向量靈敏度的自適應迭代計算

陳錦洪, 鐘慧湘, 吳柏生

(廣東工業(yè)大學 機電工程學院, 廣州 510006)

在結(jié)構(gòu)動力學模型校正、優(yōu)化和損傷檢測等領(lǐng)域, 均需用到特征值和特征向量的導數(shù)[1-3].其中, 特征值的導數(shù)計算較容易, 但特征向量的導數(shù)計算則較復雜, 這主要是由于特征向量導數(shù)控制方程的系數(shù)為奇異矩陣所致.目前, 關(guān)于特征值和特征向量導數(shù)的計算方法可分為精確解法和近似解法兩類.精確解法主要有模態(tài)疊加法[4]、Nelson方法[5]和改進的Nelson方法[6]等.模態(tài)疊加法需已知整個結(jié)構(gòu)所有振型信息才能準確計算特征值與特征向量的導數(shù), 但不易獲得工程結(jié)構(gòu)的全部振型信息.Nelson方法和改進的Nelson方法直接改變系數(shù)矩陣的奇異性, 前者僅適合單特征值的特征向量導數(shù)計算, 后者可用于單和重特征值的特征向量導數(shù)計算.但這類方法在計算每個頻率對應的特征向量導數(shù)時均需對系數(shù)矩陣進行換行換列, 且需分解新形成的矩陣, 在編程和實施上均較繁瑣.Yang等[7]提出一種計算特征向量靈敏度的方法, 但未討論重特征值的情況, 且引入的正則項破壞了原有系數(shù)矩陣的稀疏性.為計算特征向量導數(shù), 人們以模態(tài)疊加法為基礎, 發(fā)展了計算特征向量導數(shù)問題的近似解法: Wu等[8]將預處理共軛梯度法(PCG)應用到特征向量導數(shù)問題中; Li等[9]通過修改系數(shù)矩陣(不同于Nelson方法和改進的Nelson方法)并利用迭代法實現(xiàn)了中間特征向量導數(shù)的計算; Lin等[2]對特征值和特征向量導數(shù)的理論和工程應用進行了較全面的綜述.

針對特征向量導數(shù)計算問題, 本文提出一種自適應迭代方法用于計算任意頻段內(nèi)特征向量的導數(shù).先自適應計算參與模態(tài)疊加所需的中間特征對, 再通過迭代方法自適應計算所需頻帶的特征向量導數(shù).本文方法僅需求解移位特征值時已完成的移位剛度矩陣分解, 無需任何其他矩陣分解.數(shù)值算例驗證了所提方法的有效性.

1 中間特征值對應特征向量導數(shù)的計算

對無阻尼系統(tǒng)自由振動, 其特征問題滿足如下方程：

(1)

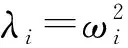
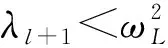
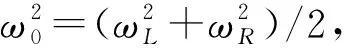
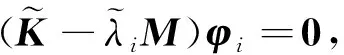
(2)

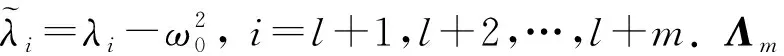
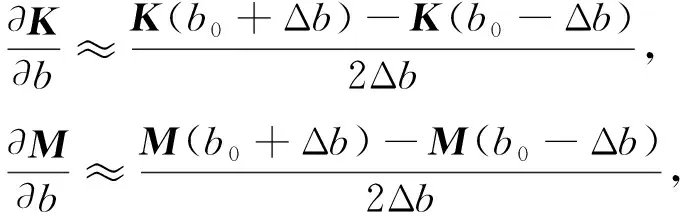
(3)

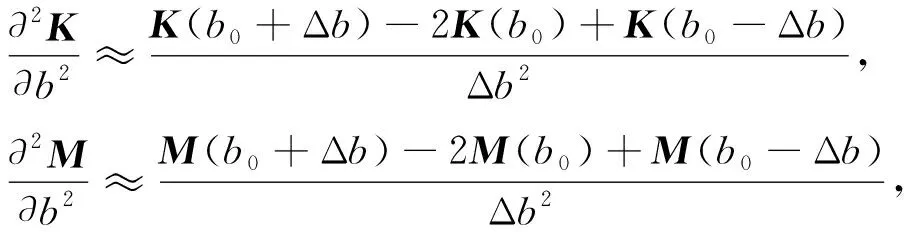
(4)

其中Δb為步長, 可通過文獻[11]確定.

當m0>1時, 對應重特征值的情況.由于其重特征值對應的特征向量不唯一, 即φs+1,φs+2,…,φs+m0的任何線性組合仍是一個特征向量, 因此需找到可定義導數(shù)的特征向量.令λ0對應的特征向量矩陣為X=(φs+1,φs+2,…,φs+m0), 則重特征值的導數(shù)?λi/?b可通過求解

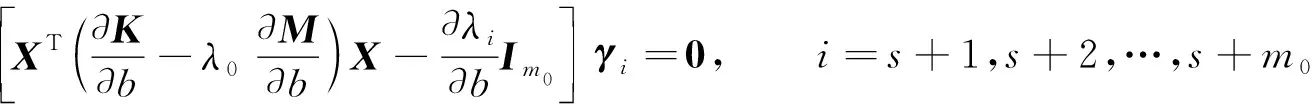
(5)

的特征值計算[12-13].假設所求重特征值的導數(shù)?λi/?b互不相同.設Γ=(γs+1,γs+2,…,γs+m0)為由方程(5)的特征向量構(gòu)成的m0階正交矩陣, 則可求導的重特征向量可表示為Z=XΓ.

設重特征向量導數(shù)的解為

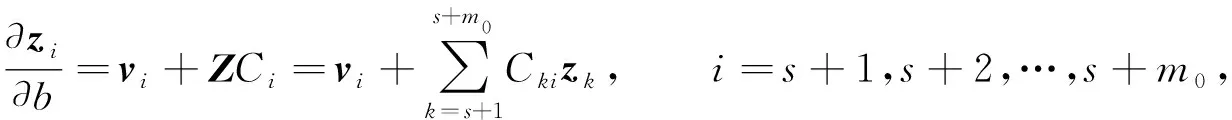
(6)

式中特解vi滿足

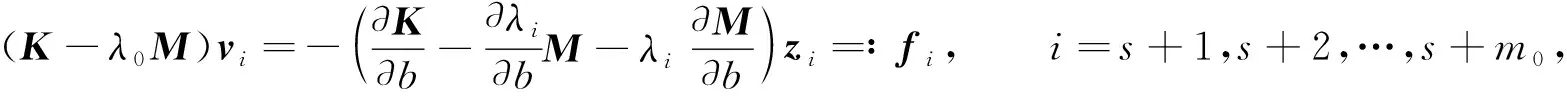
(7)

當特解vi確定后, 系數(shù)Ci可由

(8)

求得.

文獻[14-15]討論了重特征值導數(shù)相同的情況, 本文只研究重特征值導數(shù)互不相同的情況, 其中m0=1對應單特征值, 其結(jié)果可簡化.

2 中間特征向量導數(shù)的自適應迭代計算

由式(7)可知,K-λ0M是秩為n-m0的n階矩陣, 其核空間由Z=(zs+1,zs+2,…,zs+m0)組成.基于Fox等[4]的模態(tài)疊加法, 特解vi(i=s+1,s+2,…,s+m0)可由所有除重頻外對應的n-m0特征向量疊加求得, 即

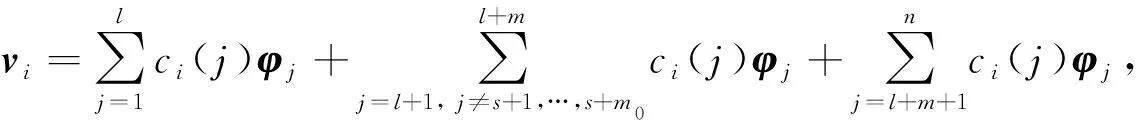
(10)

其中

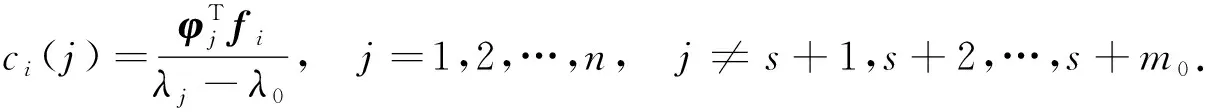
(11)

將方程(10)改寫為

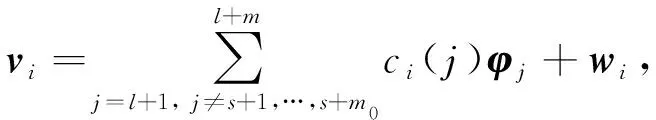
(12)

其中

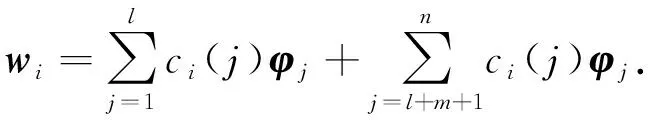
(13)

模態(tài)疊加法需知道全部的模態(tài)信息, 但對大規(guī)模有限元模型, 不易求解全部模態(tài).所以僅能對特解的一部分, 即中間特征向量Φm中對應的部分實施模態(tài)疊加；其補償部分wi用

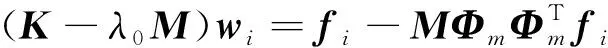
(14)

求解.由于K-λ0M為奇異矩陣, 因此文獻[9]將式(14)修改為

(15)

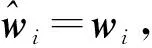
文獻[9]給出了迭代式

wi,k+1=Gwi,k+f,k=0,1,2,…,

(16)

其中

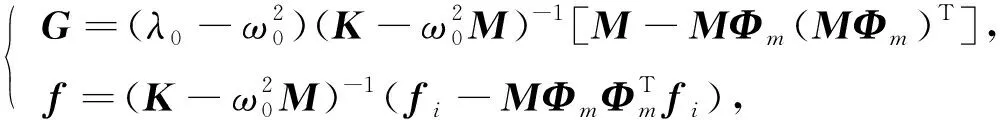
(17)

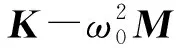
迭代矩陣G的譜半徑

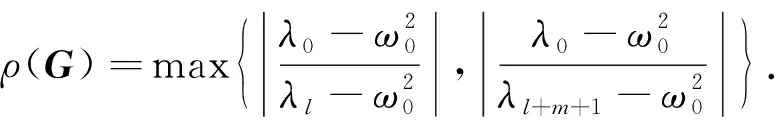
(18)

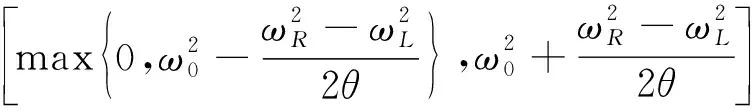
(19)

內(nèi), 這些中間特征對確定后, 由譜半徑公式(18)可知, 在頻帶[ωL,ωR]內(nèi)的特征對, 迭代矩陣的譜半徑小于θ.

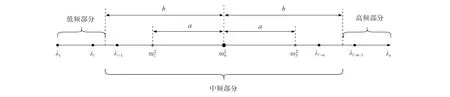
圖1 特征值分布Fig.1 Eigenvalue distribution

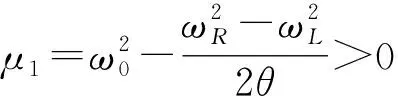
由式(16), 定義wi,k在第k次迭代后的殘量相對于右端項fi的相對殘差為

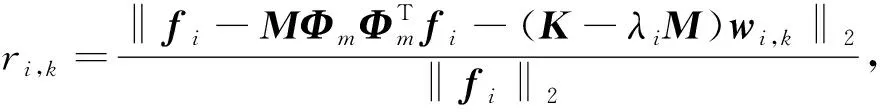
(20)

其中‖‖2為2-范數(shù), 并取wi,0=0.定義容許誤差ε, 當ri,k<ε時, 迭代解wi,k滿足收斂精度要求.

基于上述討論, 求解指定頻帶內(nèi)重特征向量導數(shù)(單特征值的情形同樣適用)的步驟如下：

1) 設定θ, 0<θ<1, 先計算由式(19)確定區(qū)間內(nèi)的特征對Λm和Φm;

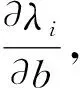
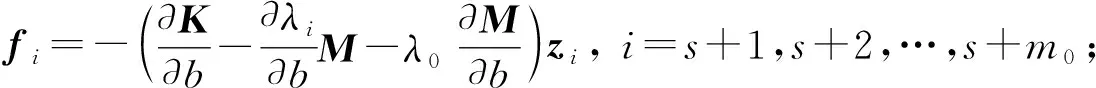
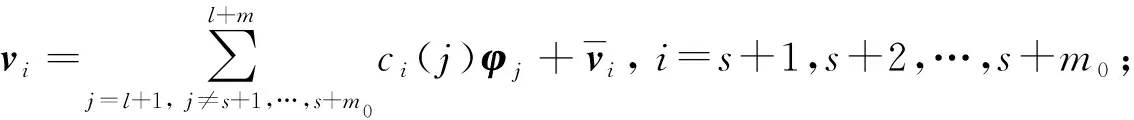
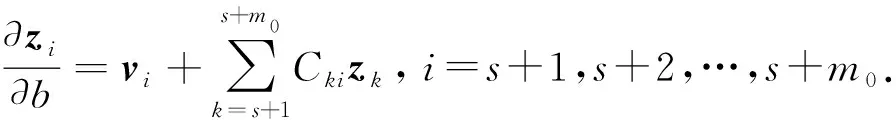
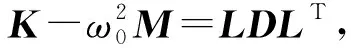
3 數(shù)值實驗

下面通過數(shù)值算例驗證本文方法的有效性.本文數(shù)值算例在配置如下的計算機上運行： 處理器為Intel(R) Xeon(R) Gold 6226R CPU@2.90 GHz 2.89 GHz(2處理器), 內(nèi)存為256 GB, 系統(tǒng)為64位Windows 10.本文方法與改進Nelson方法的編程均采用軟件MATLAB R2021a實現(xiàn).采用MALTAB的eigs函數(shù)(采用默認收斂容差)求解移位特征值.相關(guān)的剛度矩陣和質(zhì)量矩陣信息由ABAQUS建模獲得.

本文方法比改進Nelson方法的優(yōu)勢通過CPU計算時間衡量, 自適應迭代方法的計算精度采用相對誤差公式衡量.定義兩特征向量導數(shù)的相對誤差

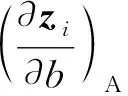
考慮如圖2所示的一個四邊固定矩形板的固有振動問題.其長度x=2 m, 寬度y=2 m, 板厚h=0.01 m.材料的彈性模量E=78 GPa, Poisson比μ=0.32, 材料密度ρ=2 770 kg/m3.將該板劃分成1 600個單元, 單元類型為Shell單元S8R5, 含31 205個自由度.以圖3單元(黑色單元)的厚度為設計變量b, 其初始值b0=0.01 m, 步長Δb=0.000 1 m.假設頻帶為[260 Hz,320 Hz], 容許誤差ε=10-4.

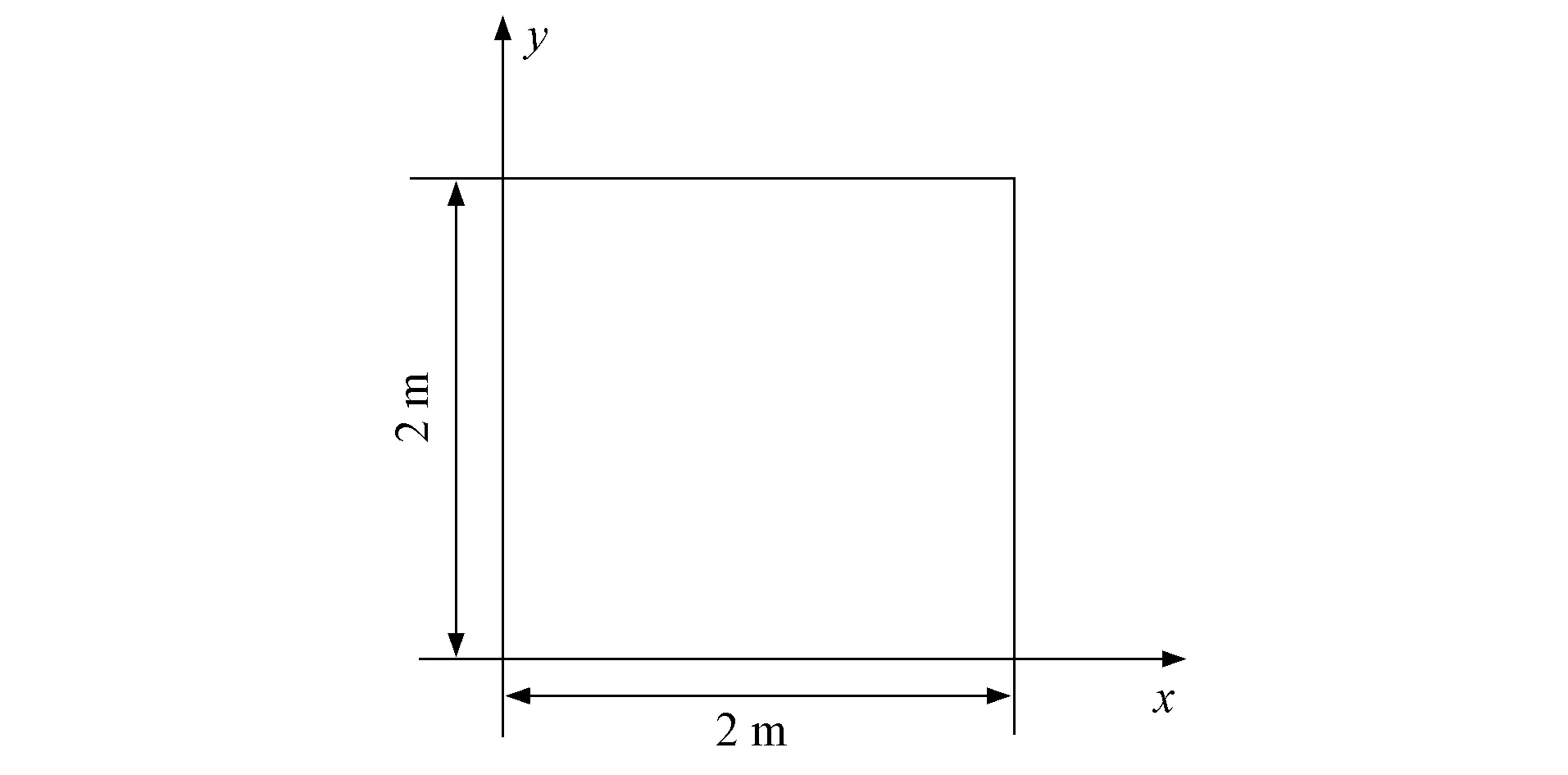
圖2 矩形板結(jié)構(gòu)Fig.2 Rectangular plate structure

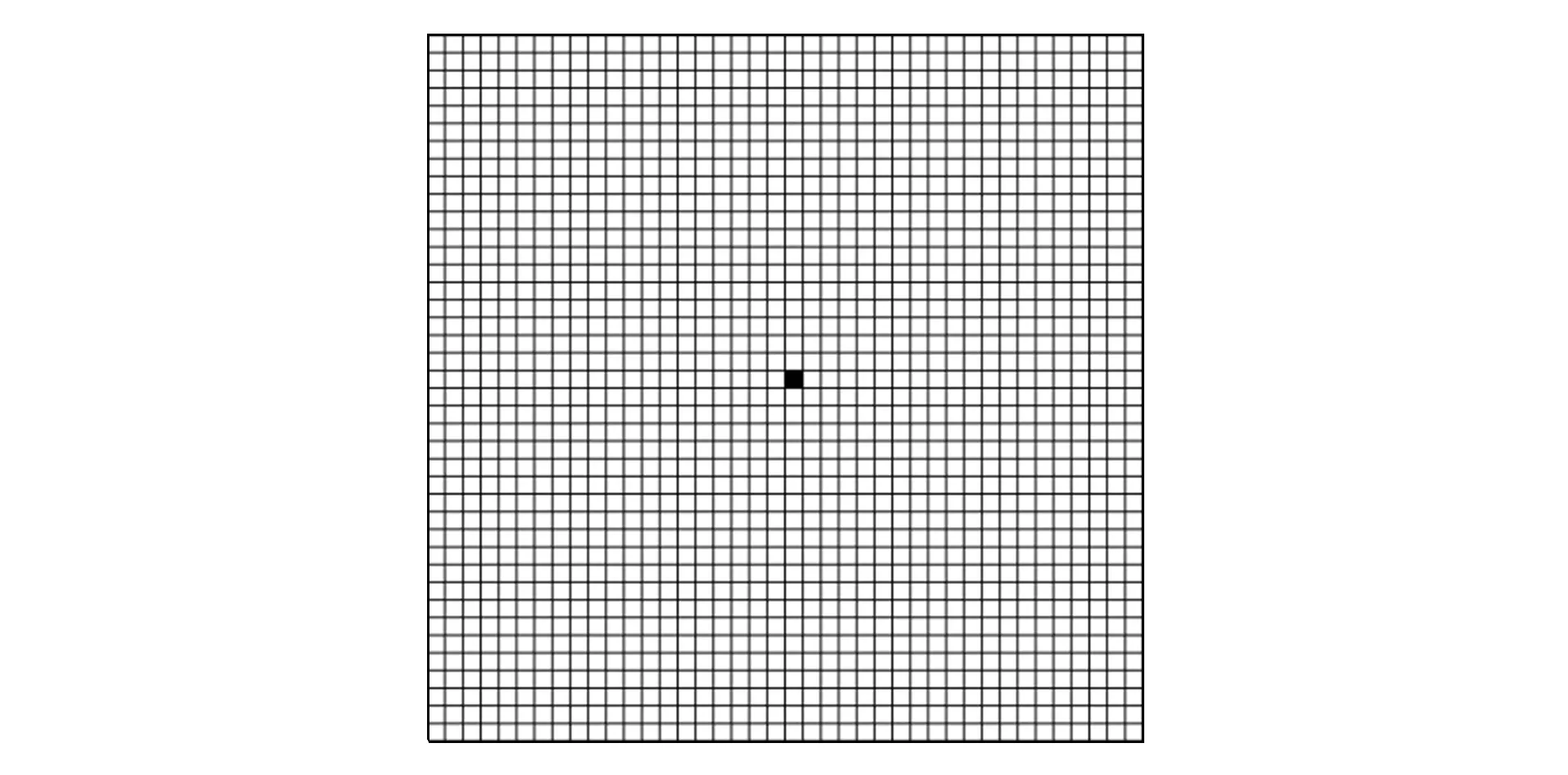
圖3 板結(jié)構(gòu)設計變量Fig.3 Design variables of plate structure

設θ=0.5.求解在區(qū)間[224.05 Hz,346.12 Hz]內(nèi)的特征對Λm和Φm.通過Sturm定理求得該區(qū)間特征對的個數(shù)為11.采用本文方法計算關(guān)注頻帶內(nèi)頻率的導數(shù)列于表1, 采用本文方法與改進Nelson方法求解特征向量導數(shù)的相對誤差列于表2.

表1 矩形板的頻率及關(guān)注頻帶內(nèi)頻率的導數(shù)

表2 關(guān)注頻帶的特征向量導數(shù)的相對誤差

由表2可見, 最大相對誤差小于0.624%.計算關(guān)注頻帶的特征向量導數(shù)的總CPU時間, 采用本文方法需81.6 s, 采用改進Nelson方法需104.2 s, 總時間約縮減了22%.

綜上所述, 針對特征向量導數(shù)計算問題, 本文提出了一種自適應迭代方法用于計算中間任意頻帶內(nèi)的特征向量導數(shù).通過設定θ值(小于1), 自適應計算參與模態(tài)疊加所需的中間特征對, 再通過迭代算法自適應求得關(guān)注頻帶內(nèi)的特征向量導數(shù).本文方法僅需在求解移位特征值時分解一次移位剛度矩陣, 無需任何其他矩陣分解.數(shù)值算例驗證了本文方法的有效性.