5類圖的優美性

唐保祥, 任 韓

(1.天水師范學院 數學與統計學院, 甘肅 天水 741001; 2.華東師范大學 數學科學學院, 上海 200062)

1 引言與預備知識

優美圖在晶體結構中的原子位置測定、物流運輸、編碼設計、通訊網絡、X射線密碼技術、天文學、導彈控制、雷達和數據庫管理等領域應用廣泛[1-2].但目前對一般圖的優美性研究尚無系統性理論.研究表明, 判定任意一個圖是否為優美圖是一個NP難問題.目前, 對圖優美性的證明一般仍用構造性方法[3-17].

最省刻度尺問題為： 設m,n為正整數, 在長為n(任意一個確定的值)厘米的無刻度尺上添加m個刻度(包括直尺兩端的刻度), 使其可以度量1～n內任何整厘米長度的尺寸, 求m的值至少是多少.該問題的一般情形目前尚未解決[17].

定義1[1]設圖G=(V,E), 若存在單射θ:V(G)→{0,1,2,…,|E(G)|}, 使得?e=uv∈E(G), 由θ′(e)=|θ(u)-θ(v)|可導出雙射θ′:E(G)→{1,2,…,|E(G)|}, 則稱圖G是優美圖,θ稱為圖G的一個優美標號,θ′稱為由θ導出的邊標號.

定義2[12-13]給定邊數的優美圖中頂點數最少的優美圖稱為極小優美圖.

把完全二部圖K2,n的頂點w與全圖K3的頂點u0連接一條邊, 再把K2,n的頂點v0與K3的頂點u0,u1,u2分別連接一條邊得到的圖記作K2,n-1-3-K3, 如圖1所示.把完全二部圖K2,n的頂點w與全圖K3的頂點u0,u1分別連接一條邊, 再把K2,n的頂點v0與K3的頂點u0,u1分別連接一條邊得到的圖記作K2,n-2-2-K3, 如圖2所示.

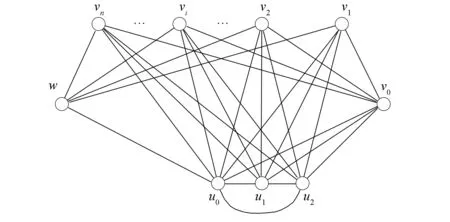
圖1 圖K2,n-1-3-K3Fig.1 Graph K2,n-1-3-K3

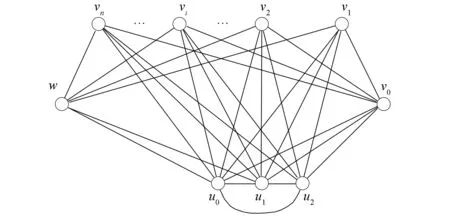
圖2 圖K2,n-2-2-K3Fig.2 Graph K2,n-2-2-K3

把完全二部圖K2,n的頂點w與全圖K3的頂點u0連接一條邊, 再把K2,n的頂點v0與K3的頂點u0,u1分別連接一條邊得到的圖記作K2,n-1-2-K3, 如圖3所示.把完全二部圖K1,n的頂點v0與K3的頂點u0,u1分別連接一條邊得到的圖記作K1,n-2-K3, 如圖4所示.把完全二部圖K1,n的頂點v0與有3個頂點的路P3的頂點u1,u0,u2分別連接一條邊得到的圖記作K1,n-3-P3, 如圖5所示.

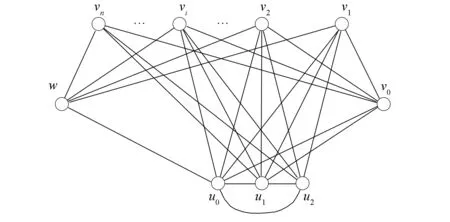
圖3 圖K2,n-1-2-K3Fig.3 Graph K2,n-1-2-K3

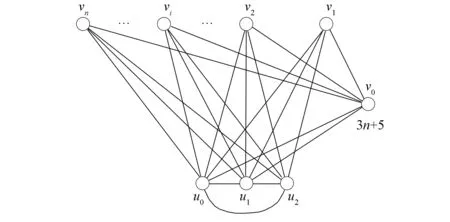
圖4 圖K1,n-2-K3Fig.4 Graph K1,n-2-K3

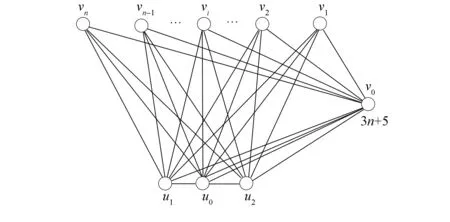
圖5 圖K1,n-3-P3Fig.5 Graph K1,n-3-P3

n個整數單位長度的直尺, 最少添加m個刻度(這m個刻度包括尺子的兩個端點), 使得能度量1～n內任何整數單位長度的尺寸, 這樣的直尺度量方式, 對應一個圖: 有m個頂點、n條邊的圖, 任意一對頂點的兩個數值較大數與較小數之差恰好是1,2,…,n.此時該圖形為一個極小優美圖.

本文證明5類結構相似但不同構的圖是優美圖.當1≤n≤5時, 圖K2,n-1-3-K3,K2,n-2-2-K3,K2,n-1-2-K3和K1,n-3-P3都是極小優美圖.因此, 每個n值對應圖的頂點標號, 均可給出對應尺長(圖的邊數)的最省刻度.圖K2,n-1-3-K3,K2,n-1-2-K3和K1,n-3-P3中n=1～5, 得到15組對應尺長最省刻度的數值.

2 主要結果

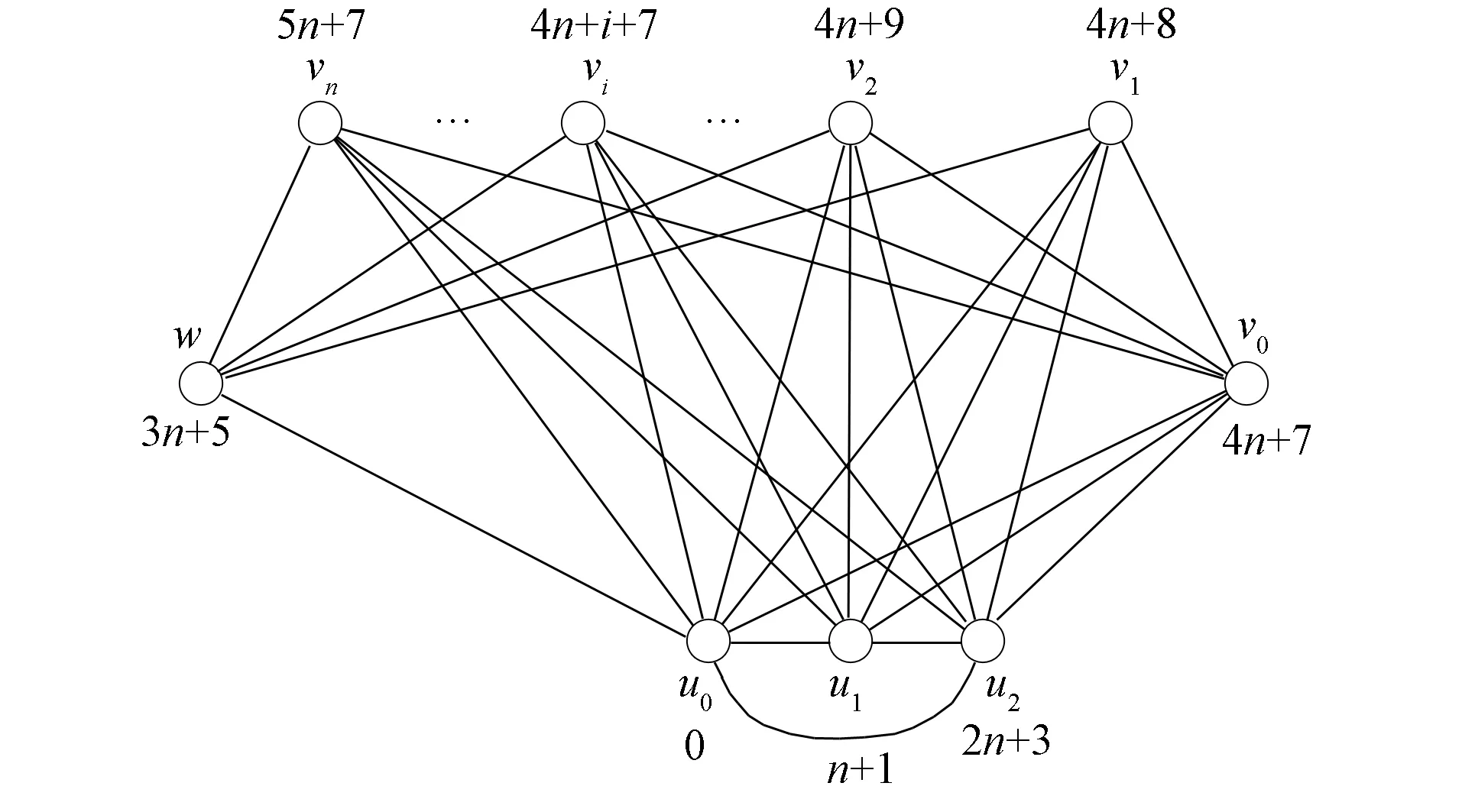
圖6 圖K2,n-1-3-K3的優美標號Fig.6 Graceful labeling of graph K2,n-1-3-K3

定理1?n∈+, 圖K2,n-1-3-K3是優美圖.

證明: 設圖K2,n-1-3-K3的頂點集合為{u0,u1,u2,w,vi|i=0,1,2,…,n}, 由圖K2,n-1-3-K3的定義知

|E(K2,n-1-3-K3)|=5n+7,

|V(K2,n-1-3-K3)|=n+5.

定義圖K2,n-1-3-K3頂點的標號θ1如下:

θ1(u0)=0,θ1(u1)=n+1,

θ1(u2)=2n+3,θ1(w)=3n+5;

θ1(vi)=4n+7+i,i=0,1,2,…,n.

圖K2,n-1-3-K3的標號θ1如圖6所示.根據標號θ1的定義, 圖K2,n-1-3-K3的集合為{u0,u1,u2,w,vi|i=0,1,2,…,n}, 定義的標號集合為{0,n+1,2n+3,4n+7+i|i=0,1,2,…,n}.所以映射θ1:V(K2,n-1-3-K3)→{0,1,2,…,5n+7}是單射.

映射θ1導出的邊標號如下:

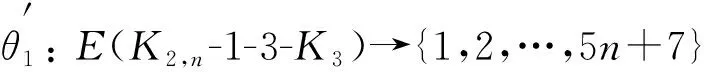
定理2?n∈+, 圖K2,n-2-2-K3是優美圖.

證明: 設圖K2,n-2-2-K3的頂點集合為{u0,u1,u2,w,vi|i=0,1,2,…,n}, 由圖K2,n-2-2-K3的定義知,

|E(K2,n-2-2-K3)|=5n+7,

|V(K2,n-2-2-K3)|=n+5.

定義圖K2,n-1-2-K3頂點的標號θ3如下:

θ2(u0)=0,θ2(u1)=n+1,θ2(u2)=2n+3,θ2(w)=3n+5;

θ2(vi)=4n+7+i,i=0,1,2,…,n.

圖K2,n-2-2-K3的標號θ2如圖7所示.

類似定理1的證明易知,θ2是圖K2,n-2-2-K3的一個優美標號, 因此圖K2,n-2-2-K3是優美圖.

定理3?n∈+, 圖K2,n-1-2-K3是優美圖.

證明: 設圖K2,n-1-2-K3的頂點集合為{u0,u1,u2,w,vi|i=0,1,2,…,n}, 由圖K2,n-1-2-K3的定義知

|E(K2,n-1-2-K3)|=5n+6,

|V(K2,n-1-2-K3)|=n+5.

定義圖K2,n-1-2-K3頂點的標號θ3如下:

θ3(u0)=0,θ3(u1)=n+1,θ3(u2)=2n+3,θ3(w)=3n+4;

θ3(vi)=4n+6+i,i=0,1,2,…,n.

圖K2,n-1-2-K3的標號θ3如圖8所示.

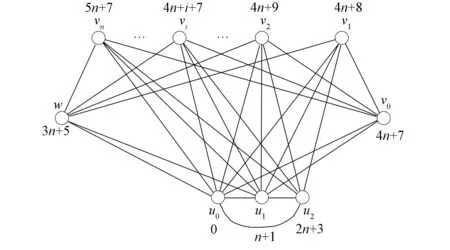
圖7 圖K2,n-2-2-K3的優美標號Fig.7 Graceful labeling of graph K2,n-2-2-K3

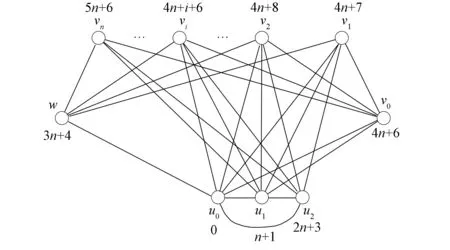
圖8 圖K2,n-1-2-K3的優美標號Fig.8 Graceful labeling of graph K2,n-1-2-K3

類似定理1的證明易知,θ3是圖K2,n-1-2-K3的一個優美標號, 所以圖K2,n-1-2-K3是優美圖.

定理4?n∈+, 圖K1,n-2-K3是優美圖.

證明: 設圖K1,n-2-K3的頂點集合為{u0,u1,u2,vi|i=0,1,2,…,n}, 由圖K1,n-2-K3的定義知,

|E(K1,n-2-K3)|=4n+5,

|V(K1,n-2-K3)|=n+4.

定義圖K1,n-2-K3頂點的標號θ4如下:

θ4(u0)=0,θ4(u1)=n+1,θ4(u2)=2n+3;

θ4(vi)=4n+5+i,i=0,1,2,…,n.

圖K1,n-2-K3的標號θ4如圖9所示.

類似定理1的證明易知,θ4是圖K1,n-2-K3的一個優美標號, 所以圖K1,n-2-K3是優美圖.

定理5?n∈+, 圖K1,n-3-P3是優美圖.

證明: 設圖K1,n-3-P3的頂點集合為{u0,u1,u2,vi|i=0,1,2,…,n}, 由圖K1,n-3-P3的定義知,

|E(K1,n-3-P3)|=4n+5,

|V(K1,n-2-K3)|=n+4.

定義圖K1,n-3-P3頂點的標號θ5如下:

θ5(u0)=0,θ5(u1)=n+1,θ5(u2)=2n+3;

θ5(vi)=3n+5+i,i=0,1,2,…,n.

圖K1,n-3-P3的標號θ5如圖10所示.

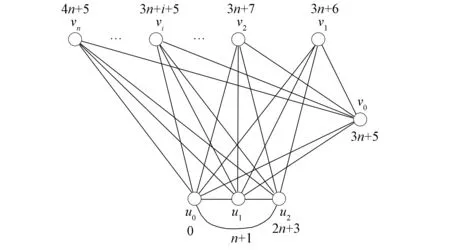
圖9 圖K1,n-2-K3的優美標號Fig.9 Graceful labeling of graph K1,n-2-K3

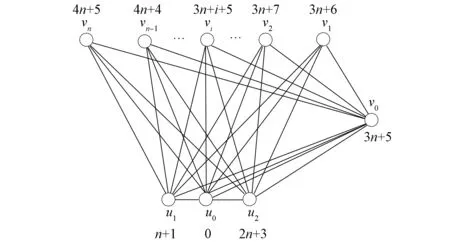
圖10 圖K1,n-3-P3的優美標號Fig.10 Graceful labeling of graph K1,n-3-P3

類似定理1的證明易知,θ5是圖K1,n-3-P3的一個優美標號, 所以圖K1,n-3-P3是優美圖.

3 應 用

文獻[12]已經證明: 邊數為m的極小優美圖G的頂點數為f(m), 則

其中[x]表示大于等于x的最小整數.

根據上述結論, 當1≤n≤5時, 圖K2,n-1-3-K3,K2,n-2-2-K3,K2,n-1-2-K3和K1,n-3-P3都是極小優美圖.因此, 每個n值對應圖的頂點標號, 都給出了對應尺長(圖的邊數)的最省刻度.圖K2,n-1-3-K3,K2,n-1-2-K3和K1,n-3-P3中n=1～5, 對應尺長的最省刻度分別列于表1～表3.

表1 K2,n-1-3-K3的邊數、頂點數及對應的最省直尺刻度值

表2 K2,n-1-2-K3的邊數、頂點數及對應的最省直尺刻度值

表3 K2,n-3-P3的邊數、頂點數及對應的最省直尺刻度值