燃料貼壁式固體超燃沖壓發(fā)動(dòng)機(jī)推力性能研究
張 皓,黃 萌,鄧 恒,田小濤,顏 密,賈勝錫
(1 西安現(xiàn)代控制技術(shù)研究所,陜西 西安 710065;2 現(xiàn)代控制技術(shù)重點(diǎn)實(shí)驗(yàn)室,陜西 西安 710065)
0 引言
作為高超聲速巡航飛行器潛在動(dòng)力系統(tǒng)之一,固體燃料超燃沖壓發(fā)動(dòng)機(jī)(以下簡(jiǎn)稱:固體超燃)具有比沖高、結(jié)構(gòu)簡(jiǎn)單、成本低、維護(hù)方便等優(yōu)點(diǎn)。與固體火箭發(fā)動(dòng)機(jī)不同,由于固體超燃具有進(jìn)氣道部件,發(fā)動(dòng)機(jī)內(nèi)部工作效率與外部飛行環(huán)境強(qiáng)相關(guān),導(dǎo)致采用固體超燃的飛行器在總體設(shè)計(jì)時(shí)無法將發(fā)動(dòng)機(jī)作為獨(dú)立部件模塊化處理[1]。采用固體超燃的高超聲速巡航飛行器總體設(shè)計(jì)高度依賴發(fā)動(dòng)機(jī)-飛行器機(jī)體一體化設(shè)計(jì)技術(shù)。內(nèi)彈道計(jì)算與設(shè)計(jì)作為固體超燃高超聲速飛行器一體化設(shè)計(jì)的關(guān)鍵技術(shù),其準(zhǔn)確計(jì)算與預(yù)估至關(guān)重要。與固體火箭發(fā)動(dòng)機(jī)不同,固體超燃內(nèi)彈道與外界環(huán)境相關(guān)性強(qiáng),且內(nèi)彈道的計(jì)算涉及到高超聲速流場(chǎng)中激波的產(chǎn)生、相交、反射,火焰穩(wěn)定區(qū)低速回流燃燒放熱,固體顆粒兩相流燃燒等物理化學(xué)現(xiàn)象,一般需要開展二維/三維數(shù)值計(jì)算進(jìn)行預(yù)測(cè)。二維/三維數(shù)值計(jì)算雖然可以較為準(zhǔn)確預(yù)測(cè)內(nèi)彈道性能,但計(jì)算時(shí)間較長(zhǎng)。在進(jìn)行內(nèi)彈道計(jì)算與設(shè)計(jì)時(shí),設(shè)計(jì)變量較多,往往需要開展多工況計(jì)算,計(jì)算時(shí)間成本較大,不利于飛行器一體化總體設(shè)計(jì)的快速迭代。一維或準(zhǔn)一維內(nèi)彈道計(jì)算模型在允許的精度范圍內(nèi),簡(jiǎn)化各個(gè)物理化學(xué)過程,考慮主要因素,能極大減少計(jì)算時(shí)間,快速對(duì)發(fā)動(dòng)機(jī)內(nèi)彈道性能進(jìn)行評(píng)估與預(yù)測(cè)。
目前,超燃沖壓發(fā)動(dòng)機(jī)的準(zhǔn)一維計(jì)算模型主要有兩類:一類是以空間為基礎(chǔ)的常微分方程組穩(wěn)態(tài)求解法[2];另一類是以時(shí)間為基礎(chǔ)的偏微分方程組的非穩(wěn)態(tài)求解法[3]。二者都考慮了超聲速流動(dòng)的主要物理過程。在此基礎(chǔ)上,張鵬等[4]對(duì)幾種公開的典型燃燒室流場(chǎng)建立了一維模型,完善了相關(guān)實(shí)驗(yàn)分析。范學(xué)軍等[5]利用一維模型開展了普通煤油、加熱煤油和超臨界煤油在超聲速流場(chǎng)中的燃燒效率研究,認(rèn)為超臨界煤油燃燒效率高于冷態(tài)煤油。陳強(qiáng)[6-7]通過實(shí)驗(yàn)數(shù)據(jù)對(duì)一維模型的釋熱模塊進(jìn)行參數(shù)優(yōu)化,并用該一維模型對(duì)燃燒室結(jié)構(gòu)進(jìn)行了優(yōu)化。王厚慶等[8]通過一維計(jì)算模型開展了超燃內(nèi)彈道計(jì)算,并以該計(jì)算結(jié)果為邊界條件輸入,對(duì)碳化硅陶瓷復(fù)合材料的燃燒室冷卻結(jié)構(gòu)進(jìn)行了優(yōu)化設(shè)計(jì)。Srinivasan等[9]對(duì)一維計(jì)算模型進(jìn)行了補(bǔ)充,主要考慮了液滴蒸發(fā)、有限速率化學(xué)反應(yīng)、傳熱與摩擦等因素對(duì)計(jì)算結(jié)果的影響。Micka等[10]基于化學(xué)熒光測(cè)量法測(cè)試了燃燒室釋熱分布,并用壁面壓力修正了一維計(jì)算模型的相關(guān)參數(shù),提高了一維模型對(duì)該類燃燒室構(gòu)型的預(yù)估精度。Tomioka等[11-12]在一維模型中加入了燃油噴注簡(jiǎn)化模型,并利用該模型,以燃燒效率、推力、摩擦阻力作為目標(biāo)參數(shù),研究了燃油噴注位置對(duì)超燃性能的影響。Kliche等[13]建立了基于Euler方程的一維非定常計(jì)算模型,該模型考慮了有限速率化學(xué)反應(yīng)模型、平衡點(diǎn)火模型的影響。
目前為止,對(duì)超聲速流場(chǎng)的一維計(jì)算模型已開展了較為豐富的研究,模型功能也較為豐富。但由于固體超燃燃燒室內(nèi)流場(chǎng)中普遍存在亞聲速-跨聲速-超聲速流動(dòng)現(xiàn)象[14],一維計(jì)算模型在進(jìn)行此類問題計(jì)算時(shí),控制方程會(huì)在聲速臨界點(diǎn)存在數(shù)學(xué)奇異性。此外,在進(jìn)行部分工況計(jì)算時(shí),由于方程組參數(shù)數(shù)量級(jí)相差過大,會(huì)引起嚴(yán)重的數(shù)值剛性問題。在進(jìn)行飛行器總體設(shè)計(jì)時(shí),外彈道計(jì)算希望將發(fā)動(dòng)機(jī)看做一個(gè)“黑盒”部件,確定的輸入對(duì)應(yīng)一個(gè)確定的輸出,對(duì)發(fā)動(dòng)機(jī)內(nèi)部工作細(xì)節(jié)并不關(guān)心。因此,文中對(duì)一維模型進(jìn)一步簡(jiǎn)化,基于能量守恒方程,建立一個(gè)以推力為目標(biāo)的零維模型,研究燃料質(zhì)量流量與空氣流量變化對(duì)貼壁式固體超燃沖壓發(fā)動(dòng)機(jī)推力的影響。
1 推力零維模型
1.1 基本假設(shè)
基于典型燃燒室構(gòu)型(圖1),建立燃料供應(yīng)量對(duì)貼壁式固體超燃沖壓發(fā)動(dòng)機(jī)推力的影響模型。為建立燃料供應(yīng)量與推力之間的零維模型,現(xiàn)假設(shè)如下:
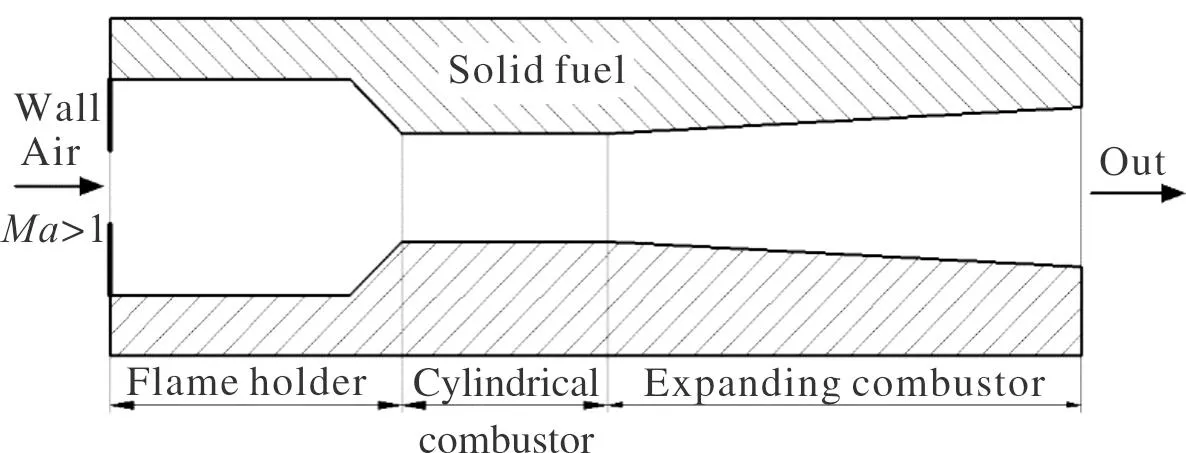
圖1 固體超燃沖壓發(fā)動(dòng)機(jī)典型構(gòu)型Fig.1 Typical configuration of sold fuel scramjet
1)不考摩擦的影響。由于燃燒室長(zhǎng)度較短,而固體燃料貼壁式超燃沖壓發(fā)動(dòng)機(jī)內(nèi)氣流流動(dòng)速度為1 000 m/s以上的,如此短的行程導(dǎo)致摩擦的影響較小。
2)認(rèn)為燃燒室內(nèi)的氣體為理想氣體。
3)不考慮發(fā)動(dòng)機(jī)的點(diǎn)火過程,認(rèn)為燃燒室內(nèi)已經(jīng)建立起穩(wěn)定工作狀態(tài)。
4)不考慮燃料的熱解過程,認(rèn)為固體燃料瞬間熱解并向燃燒室內(nèi)注入燃料氣體。
1.2 模型建立
基于以上假設(shè),根據(jù)能量守恒原則,可以列出方程:
(1)
根據(jù)質(zhì)量守恒,可以列出方程:
(2)
式中:ρe為出口氣流密度;ue為出口氣流速度;Ae為燃燒室出口截面積。
根據(jù)理想氣體定律:
Pe=ρeRTe
(3)
式中:Pe為出口靜壓;R為氣體常數(shù);Te為出口靜溫。
根據(jù)總溫與靜溫的等熵關(guān)系式,有如下方程:
(4)
式中:k為比熱比;M為出口馬赫數(shù)。
馬赫數(shù)可以通過式(5)計(jì)算:
(5)
聯(lián)立求解式(1)~式(5),可得:
(6)
按照文獻(xiàn)[15]中的方程計(jì)算地面直連試驗(yàn)的發(fā)動(dòng)機(jī)推力為:
(7)
式中Pa為出口反壓,即大氣壓。
聯(lián)立式(5)和式(7),可得出口馬赫數(shù)的計(jì)算方程:
(8)
1.3 模型驗(yàn)證
對(duì)比Ben-Yakar的試驗(yàn)數(shù)據(jù)[15]與上節(jié)推力零維模型的計(jì)算結(jié)果以驗(yàn)證該模型的正確性。根據(jù)Yakar的實(shí)驗(yàn)條件,取計(jì)算條件如表1所示。

表1 根據(jù)Yakar實(shí)驗(yàn)確定的計(jì)算條件Table 1 Computational condition determined based on Yakar′s experiment
推力零維模型計(jì)算所得的理論推力曲線與Yakar的實(shí)驗(yàn)結(jié)果對(duì)比如圖2所示。從圖中可以發(fā)現(xiàn),理論推力與Yakar的實(shí)驗(yàn)推力結(jié)果總體吻合的較好。理論推力與實(shí)驗(yàn)結(jié)果相比,理論推力整體偏低,且隨著發(fā)動(dòng)機(jī)工作過程的進(jìn)行,理論推力與實(shí)驗(yàn)結(jié)果偏差逐漸增大。這可能是由于零維推力模型計(jì)算中只考慮了平均燃面退移速率,且使用了平均燃燒效率造成的。
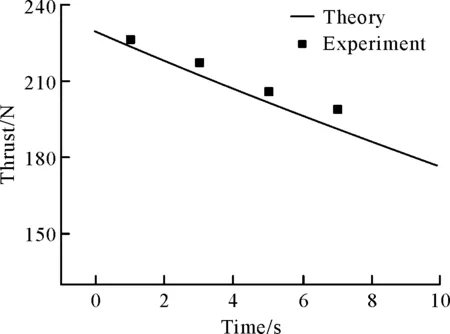
圖2 推力對(duì)比Fig.2 Thrust contrast
零維推力模型的馬赫數(shù)和出口速度與Yakar的實(shí)驗(yàn)結(jié)果對(duì)比如圖3和圖4所示。從圖中可以看出,出口馬赫數(shù)的理論結(jié)果較實(shí)驗(yàn)值整體偏低,而出口速度的計(jì)算結(jié)果與實(shí)驗(yàn)中吻合的較好。文中的零維推力模型主要用于研究空氣流量與燃料供應(yīng)量對(duì)推力的影響,因此在建立模型時(shí)未考慮燃料的熱解行為,而是將燃料供應(yīng)量作為輸入量用于發(fā)動(dòng)機(jī)推力的計(jì)算。零維推力模型未考慮摩擦的影響,導(dǎo)致計(jì)算的理論結(jié)果偏低。但從圖2和圖4可以看出,理論結(jié)果與實(shí)驗(yàn)結(jié)果偏差較小,且趨勢(shì)一致,因此,建立的零維推力模型是考慮了固體超燃工作過程中的主要因素,具有一定的精度,可以用來初步研究空氣流量與燃料供應(yīng)量對(duì)發(fā)動(dòng)機(jī)推力的影響。
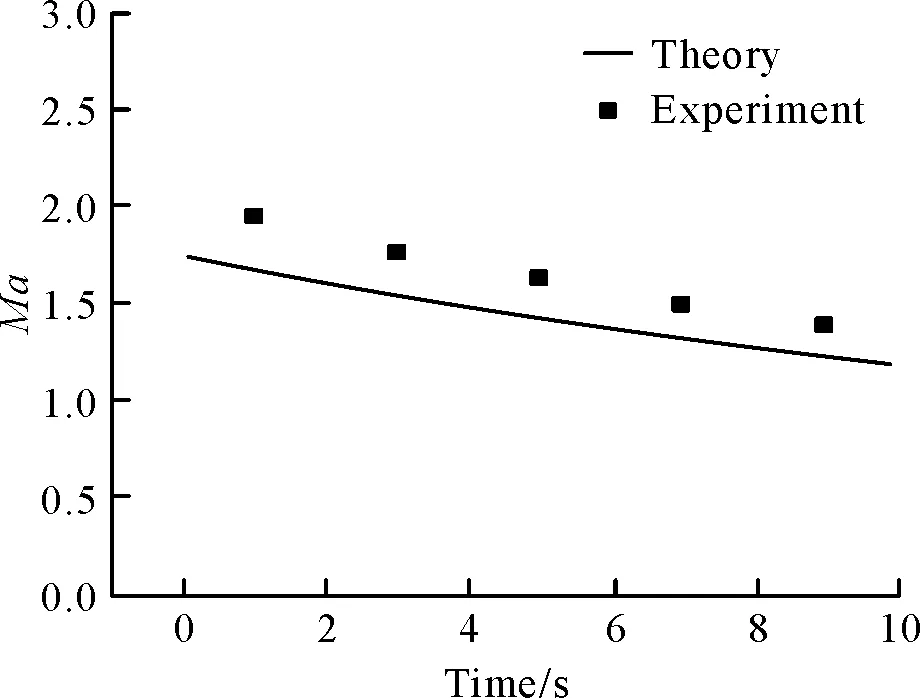
圖3 馬赫數(shù)對(duì)比Fig.3 Mach contrast
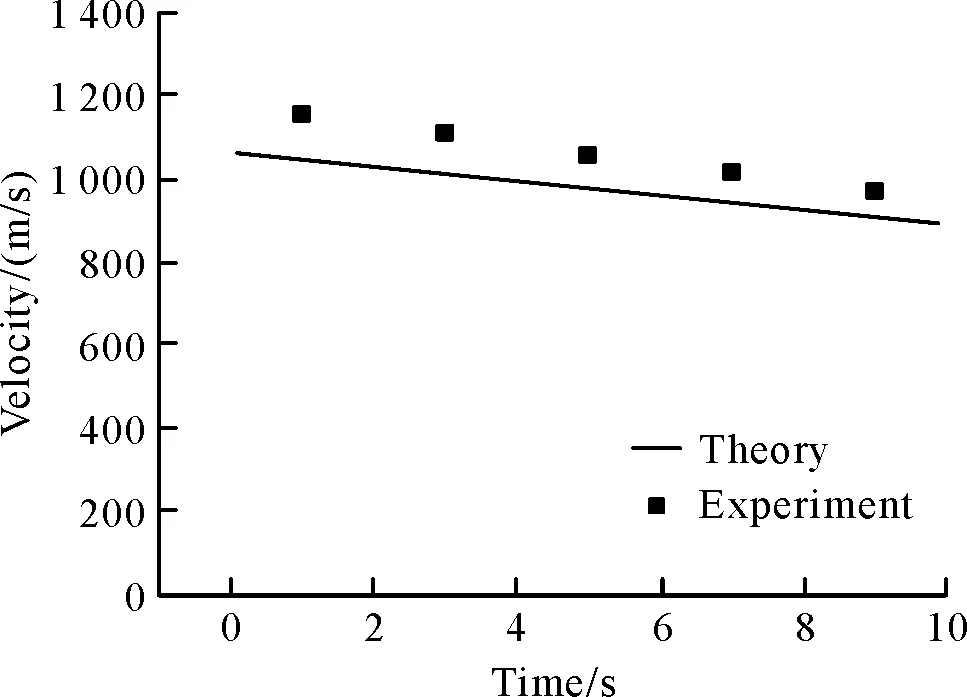
圖4 出口速度對(duì)比Fig.4 Outlet velocity contrast
2 結(jié)果與討論
將式(6)代入式(7)中可得:
(9)
式中:De,0為發(fā)動(dòng)機(jī)出口初始直徑;而Ae可表示為:
(10)
當(dāng)t=0時(shí),
(11)
將式(11)代入式(9)中可得:
(12)
對(duì)式(12)求關(guān)于De,0的導(dǎo)數(shù)可得:
(13)
整理式(13)得:
(14)
在式(14)中,顯然有:
(15)
那么對(duì)于任意的De,0,式(16)成立:
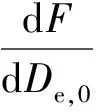
(16)
由式(16)可知,初始出口直徑越大,推力越小。該結(jié)論在李彪[16]的數(shù)值仿真計(jì)算結(jié)果中也有所體現(xiàn)。李彪的計(jì)算模型與文中討論的固體燃料超燃沖壓發(fā)動(dòng)機(jī)典型構(gòu)型與圖1相同,因此,擴(kuò)張半角越大,出口的初始直徑越大。推力與比沖隨著出口的初始直徑下降,這也符合式(16)的結(jié)論。
為研究在貼壁式固體燃料超燃沖壓發(fā)動(dòng)機(jī)燃燒室工作過程中空氣流量與燃料質(zhì)量流量的變化對(duì)推力的影響。對(duì)式(12)求時(shí)間t的導(dǎo)數(shù):
(17)
其中,
(18)
只要求出式(17)的零點(diǎn),即式(19)的解,便可以了解推力的變化過程。
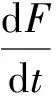
(19)
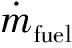
(20)
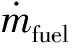
對(duì)式(20)求時(shí)間t的導(dǎo)數(shù):
(21)
假設(shè)入口空氣質(zhì)量流量為:
(22)
則有:
(23)
系數(shù)a,b,c的物理含義分別為:系數(shù)a與燃燒過程中燃面退移速率與燃面面積相關(guān);系數(shù)b為燃燒室初始時(shí)刻燃面面積與燃面退移速率的乘積;系數(shù)c為空氣質(zhì)量流量。通過設(shè)計(jì)不同的燃燒室燃面構(gòu)型及選用不同燃面退移速率的固體燃料,可以得到不同的a,b值。需要注意的是,系數(shù)a有負(fù)值,而系數(shù)b和系數(shù)c必須是正值才有意義。
對(duì)式(19)使用4-5階龍格庫塔法迭代求解,所得零點(diǎn)為t*,稱之為零點(diǎn)時(shí)間。圖5所示為零點(diǎn)時(shí)間t*隨系數(shù)a的變化曲線。從圖中可以看出,當(dāng)設(shè)定b=0.04和c=0.5時(shí),不同系數(shù)a下的零點(diǎn)時(shí)間t*不同,且t*與系數(shù)a呈現(xiàn)正相關(guān)特性。當(dāng)t*<0時(shí),則在t>0的范圍內(nèi)不存在零點(diǎn)時(shí)間,即推力F在t>0的時(shí)間段內(nèi)是單調(diào)的;而當(dāng)t*>0時(shí),在t>0的時(shí)間段內(nèi)存在零點(diǎn);當(dāng)0
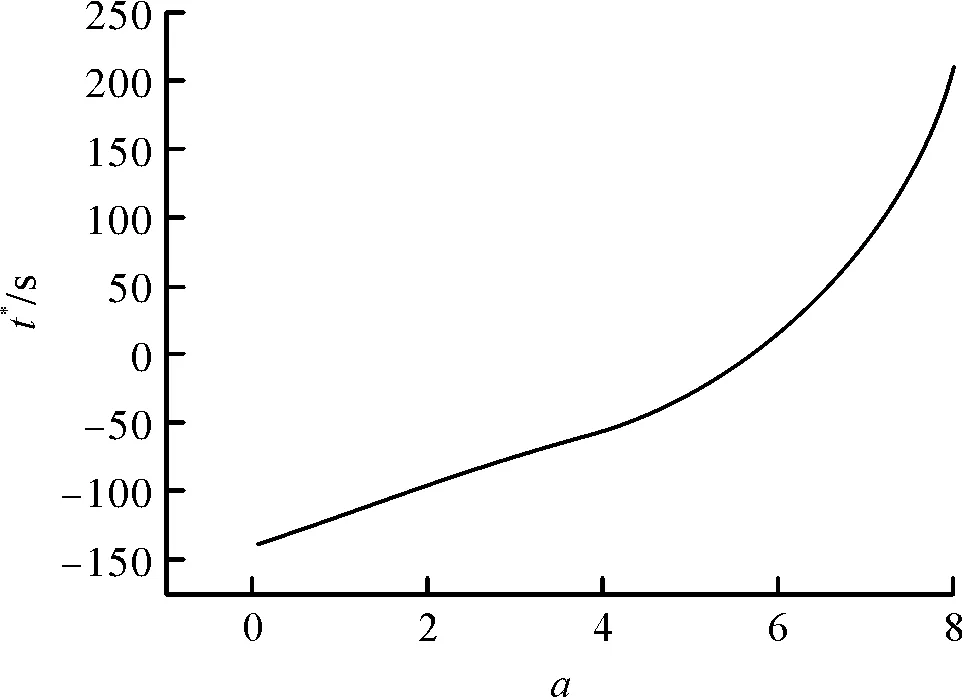
圖5 零點(diǎn)時(shí)間隨系數(shù)a的變化曲線Fig.5 Zero-point time varies with a
設(shè)b=0.04,c=0.5。當(dāng)系數(shù)a=0時(shí)的推力曲線如圖6所示。a=0表示燃料質(zhì)量流量不隨時(shí)間變化,此時(shí)零點(diǎn)時(shí)間t*<0,從圖中可以看出,這種情況下推力會(huì)隨時(shí)間逐漸降低,且降低幅度明顯,在20 s時(shí),理論推力就已經(jīng)降低了30%左右。到50 s時(shí),理論推力下降程度已經(jīng)超過了初始推力的一半。
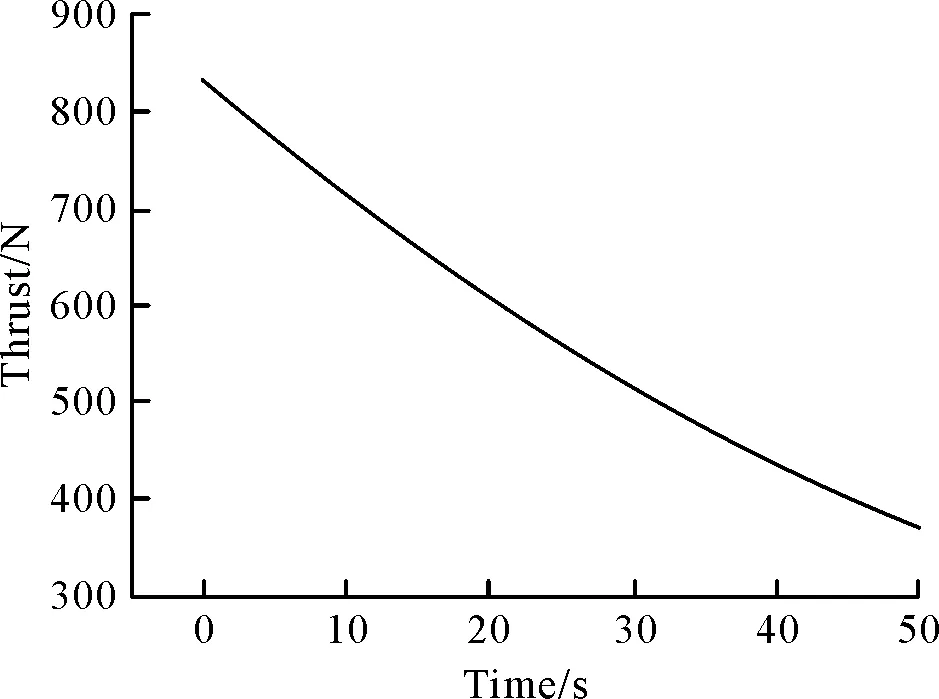
圖6 系數(shù)a=0時(shí)的推力曲線Fig.6 Thrust curve when a=0
當(dāng)系數(shù)a=0.002時(shí)的推力曲線如圖7所示。
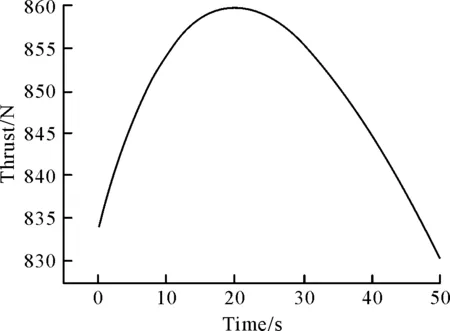
圖7 系數(shù)a=0.002時(shí)的推力曲線Fig.7 Thrust curve when a=0.002
由圖5可知,此時(shí)零點(diǎn)時(shí)間t*>0。則在t>0的時(shí)間段內(nèi)存在推力變化率為0的點(diǎn)。從圖7可以明顯看出,推力隨時(shí)間先增大,在20 s左右到達(dá)推力的峰值,然后推力開始下降。雖然這種情況下的推力有增加的趨勢(shì),但初始推力與峰值推力相差不大。在50 s 的工作時(shí)間內(nèi),推力整體變化的幅值不大。
當(dāng)系數(shù)a=0.003時(shí)的推力曲線如圖8所示。在這種情況下,推力在前50 s內(nèi)會(huì)一直增加,且推力增加幅度較a=0.002情況有明顯增大。雖然推力在前50 s內(nèi)一直增大,但從圖5中可以看出,這種情況下存在零點(diǎn)時(shí)間t*,即存在一個(gè)推力的峰值,在到達(dá)峰值前,推力會(huì)一直上升。
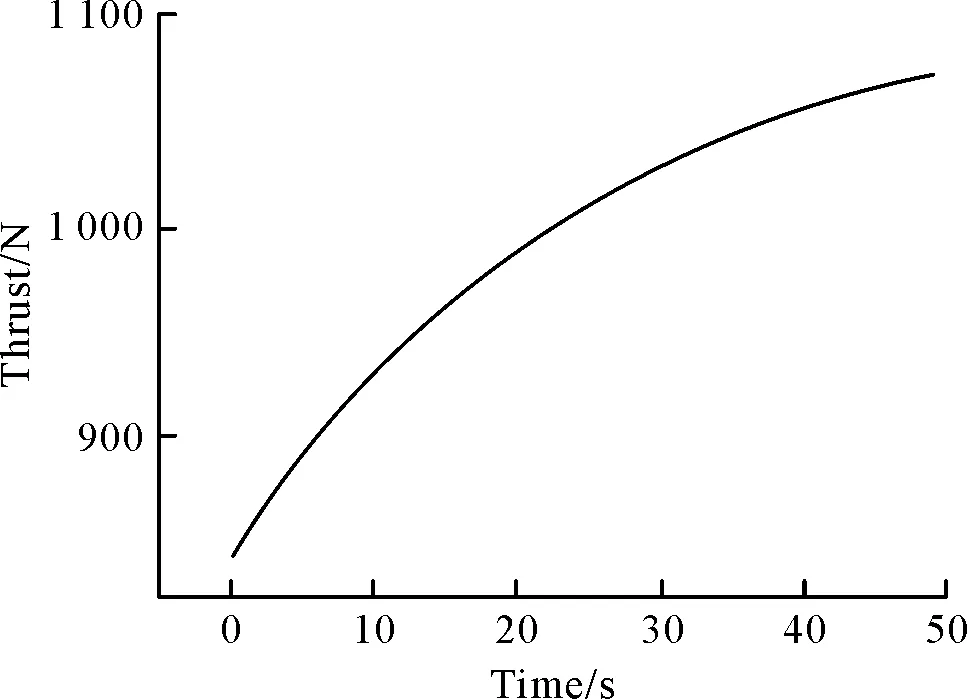
圖8 系數(shù)a=0.002時(shí)的推力曲線Fig.8 Thrust curve when a=0.003
從上述關(guān)于系數(shù)a對(duì)推力影響的討論中,可以了解到在質(zhì)量流量恒定的情況下,推力會(huì)隨著時(shí)間一直降低;選取一個(gè)合適的系數(shù)a可以讓推力在工作期間的變化幅度小很多,而選取較大的系數(shù)a會(huì)使得推力在發(fā)動(dòng)機(jī)工作期間迅速增大,且系數(shù)a越大,推力的峰值到來越晚。
下面討論系數(shù)b對(duì)推力的影響。在系數(shù)a=0.002,c=0.5的計(jì)算條件下,不同系數(shù)b下的零點(diǎn)時(shí)間t*如圖9所示。
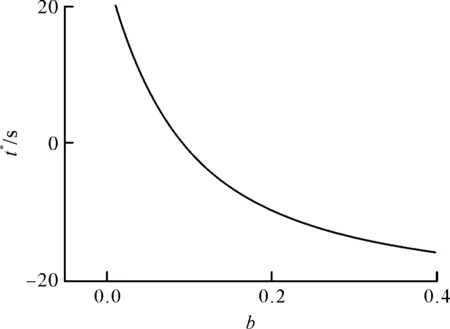
圖9 不同系數(shù)b下的零點(diǎn)時(shí)間t*Fig.9 Zero-point time varies with b
零點(diǎn)時(shí)間t*隨系數(shù)b的變化趨勢(shì)與零點(diǎn)時(shí)間t*隨系數(shù)a的變化趨勢(shì)相反。系數(shù)b的取值較小時(shí)t*>0,即推力存在一個(gè)峰值,使得推力先增大后減小。當(dāng)b的取值較大時(shí),t*<0,此時(shí)推力隨時(shí)間變化沒有峰值,推力隨時(shí)間變化呈現(xiàn)單調(diào)性。
當(dāng)b=0.03時(shí),推力隨時(shí)間的變化曲線如圖10所示,此時(shí)t*>0,即推力存在一個(gè)峰值。從圖中可以得知,推力在初始時(shí)刻的大小為760 N,在25 s前推力隨時(shí)間緩慢增加,在25 s左右時(shí)達(dá)到推力峰值,隨后開始緩慢下降。從0~25 s和25~50 s的推力曲線對(duì)比可以看出,推力上升的幅度要高于推力下降的幅度。
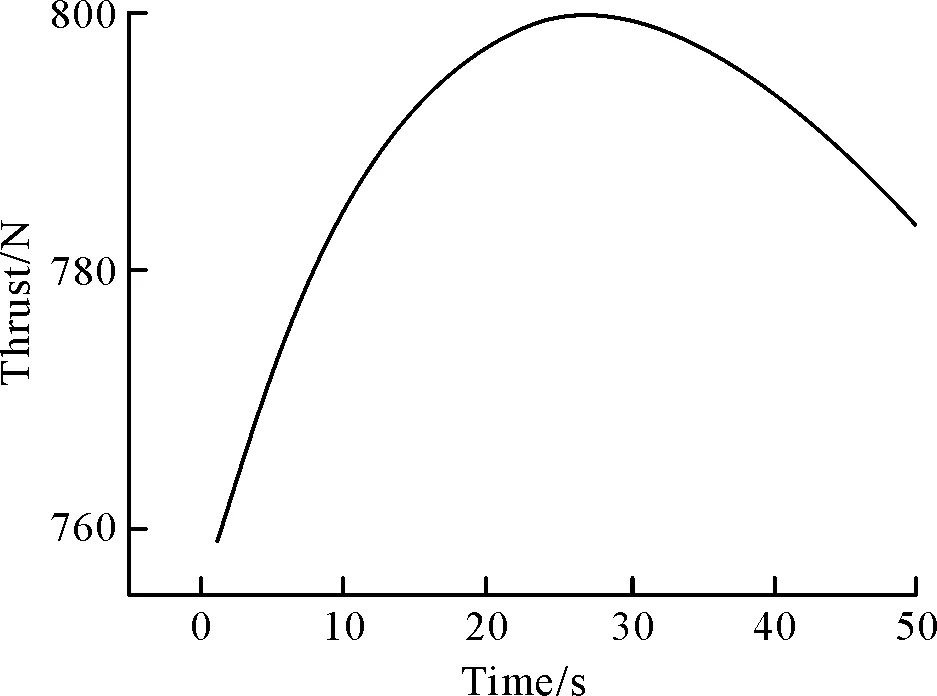
圖10 系數(shù)b=0.03時(shí)的推力曲線。Fig.10 Thrust curve when b=0.03
當(dāng)b=0.1時(shí)的推力隨時(shí)間變化曲線如圖11所示,該種情況下t*<0,即在發(fā)動(dòng)機(jī)工作過程中不存在推力峰值,推力隨時(shí)間單調(diào)變化。從圖中可知,推力在初始時(shí)刻的大小約為1 260 N,隨著時(shí)間的退移,推力一直下降,到50 s時(shí),推力已經(jīng)下降到1 120 N左右。通過對(duì)比圖10和圖11中推力的變化幅度,可以發(fā)現(xiàn)推力在單調(diào)變化時(shí)變化幅度較大。
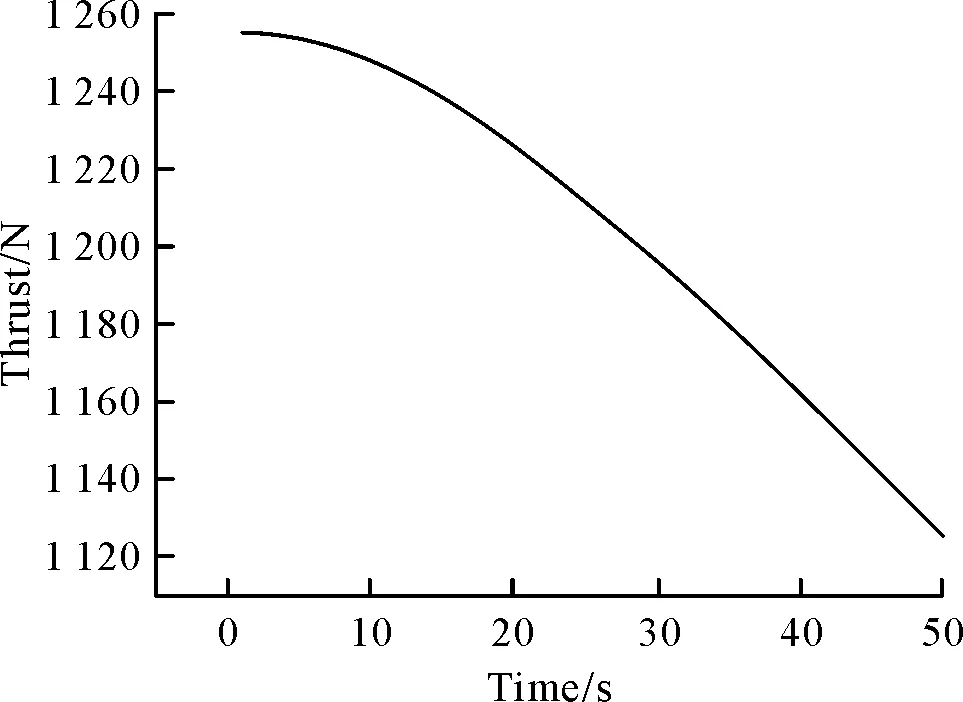
圖11 系數(shù)b=0.1的推力曲線圖Fig.11 Thrust curve when b=0.1
為考察系數(shù)a,b,c對(duì)推力變化幅度的影響,定義推力變化率如下:
(24)
式中:Fmax為工作時(shí)間內(nèi)的最大推力;Fmin為工作時(shí)間內(nèi)的最小推力;F|t=0為初始時(shí)刻的推力。
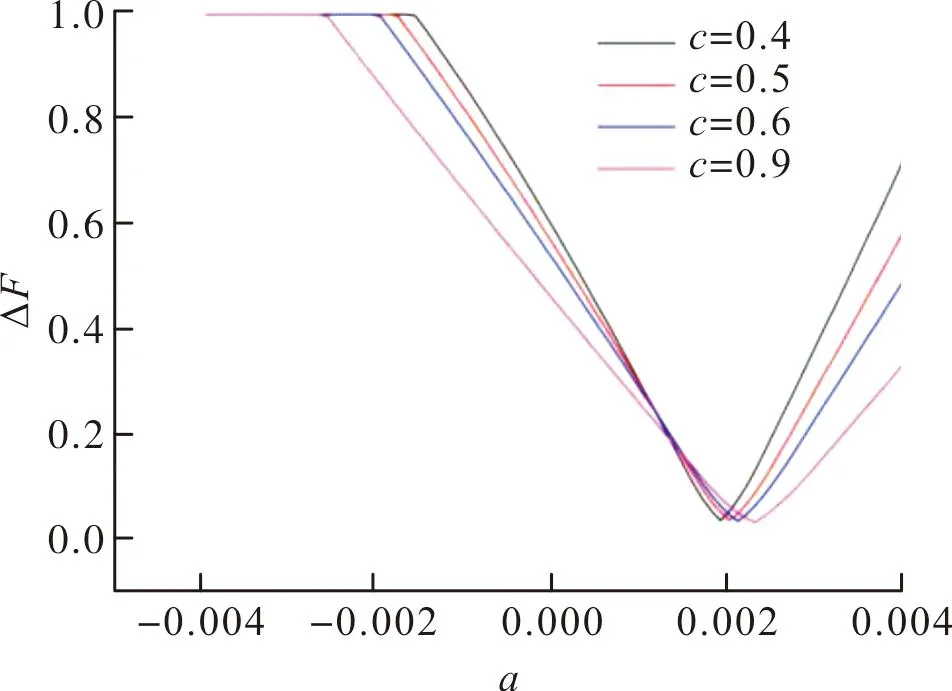
當(dāng)系數(shù)b=0.04,c=0.5時(shí)推力變化率隨系數(shù)a的變化曲線如圖12所示。推力變化率ΔF為1的情況對(duì)應(yīng)于推力在工作期間下降為0的理論極限情況。從圖中可以看出,當(dāng)系數(shù)a=0.002時(shí),推力變化率ΔF最小;當(dāng)a<0.002時(shí),推力變化率隨著系數(shù)a的增大而降低;當(dāng)系數(shù)a>0.002時(shí),推力變化率ΔF會(huì)隨著系數(shù)a的增大而增大。
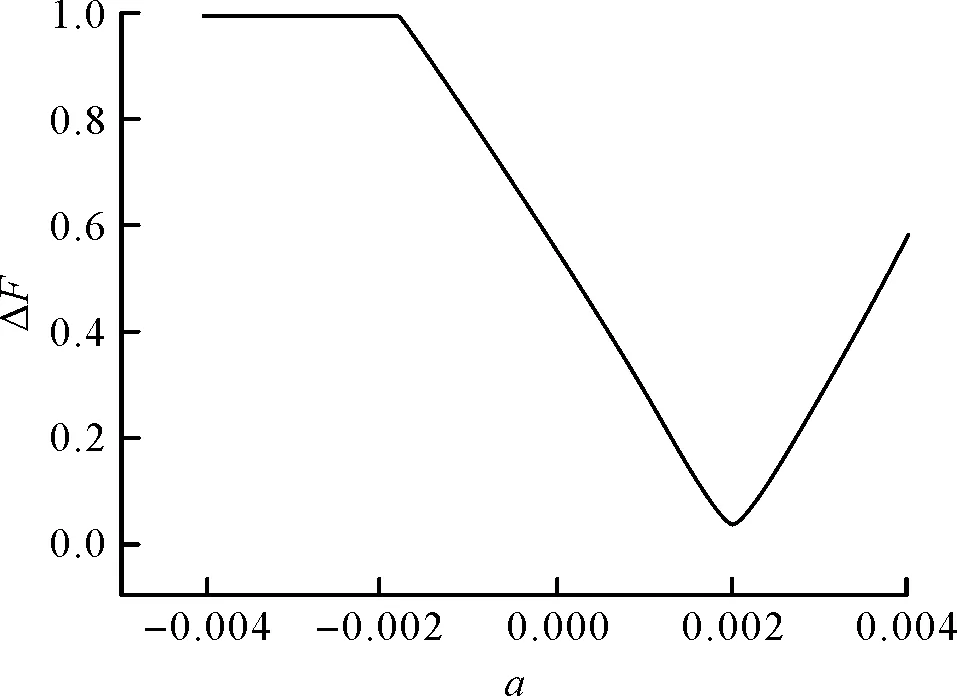
圖12 推力變化率隨系數(shù)a的變化曲線Fig.12 Curve of thrust change rate with a
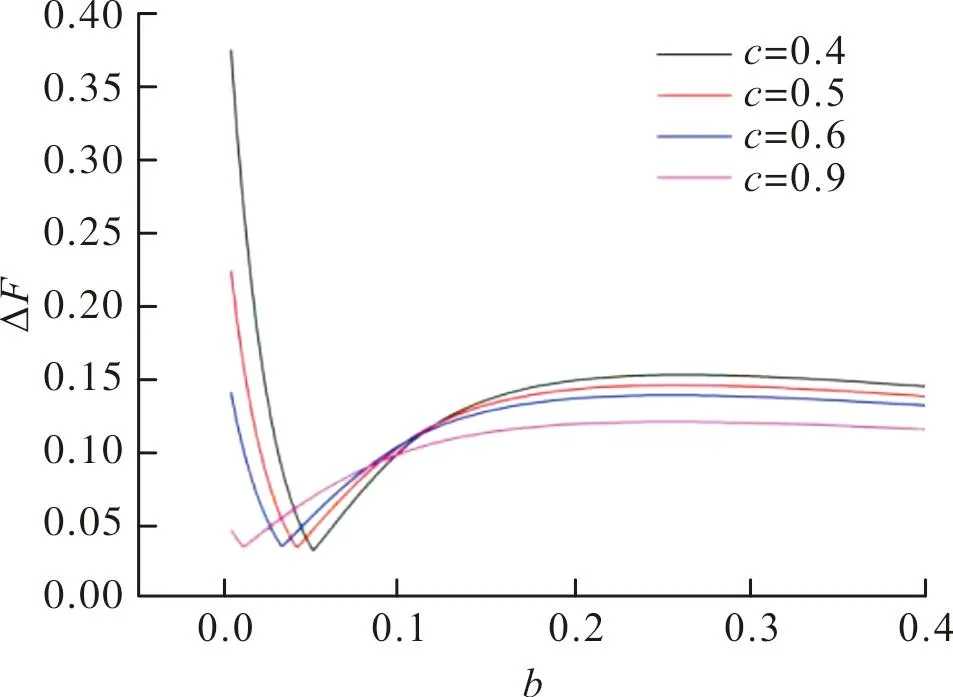
當(dāng)系數(shù)a=0.002,c=0.5時(shí)推力變化率ΔF隨系數(shù)b的變化曲線如圖13所示。當(dāng)b=0.04時(shí),推力變化率ΔF最小;當(dāng)b<0.04時(shí),推力變化率ΔF隨系數(shù)b的增加而降低;而當(dāng)b>0.04后,推力變化率ΔF隨著系數(shù)b的增加先增加,然后趨于平穩(wěn)。對(duì)比圖12和圖13可以發(fā)現(xiàn),系數(shù)a對(duì)推力變化率ΔF的影響要遠(yuǎn)遠(yuǎn)強(qiáng)于系數(shù)b。
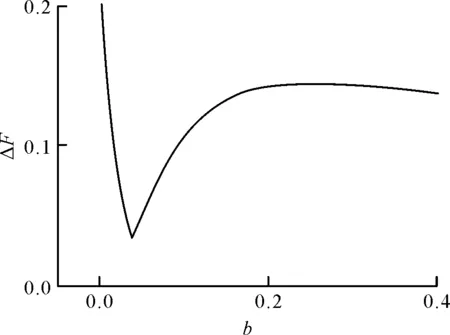
圖13 推力變化率隨系數(shù)b的變化曲線Fig.13 Curve of thrust change rate with b
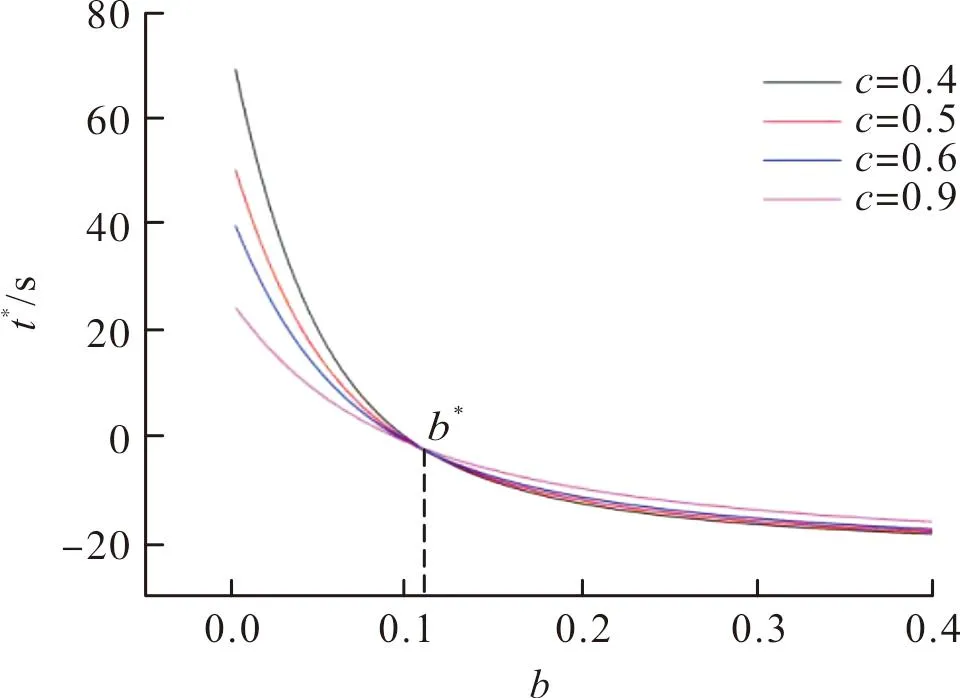
當(dāng)系數(shù)c發(fā)生變化時(shí),零點(diǎn)時(shí)間隨系數(shù)a和系數(shù)b的改變而變化的曲線如圖14和圖15所示。圖中a*和b*表示零點(diǎn)時(shí)間t*=0時(shí)的系數(shù)a和系數(shù)b,稱之為系數(shù)a,b的臨界值。從圖中可以發(fā)現(xiàn),不同的系數(shù)c下,臨界值a*和b*幾乎不發(fā)生變化。且在a 圖14 不同系數(shù)c下的零點(diǎn)時(shí)間t*隨系數(shù)a增加而變化的曲線(b=0.04)Fig.14 Zero-point time varies with a under different c(b=0.04) 圖15 不同系數(shù)c下的零點(diǎn)時(shí)間t*隨系數(shù)b增加而變化的曲線(a=0.002)Fig.15 Zero-point time varies with b under different c(a=0.002) 當(dāng)系數(shù)c發(fā)生變化時(shí),推力變化率ΔF隨系數(shù)a和系數(shù)b的改變而變化的曲線如圖16和圖17所示。 圖16 不同系數(shù)c下的推力變化率隨系數(shù)a增加而變化的曲線(b=0.04)Fig.16 Thrust change rate varies with a under different c(b=0.04) 圖17 不同系數(shù)c下的推力變化率隨系數(shù)b增加而變化的曲線(a=0.002)Fig.17 Thrust change rate varies with b under different c(a=0.002) 從圖中可以看出,當(dāng)系數(shù)c增大時(shí),在相同的系數(shù)a或系數(shù)b處,推力變化率ΔF都降低了,這說明增大空氣質(zhì)量流量可以使固體燃料超燃沖壓發(fā)動(dòng)機(jī)推力更加穩(wěn)定。且從圖中還可以看出,在推力變化率較大的系數(shù)a和系數(shù)b處,增大系數(shù)c降低推力變化率的效果更加明顯。 建立了固體超燃沖壓發(fā)動(dòng)機(jī)的零維推力模型,系統(tǒng)研究了燃料質(zhì)量流量與空氣流量對(duì)發(fā)動(dòng)機(jī)推力的影響。 固體超燃沖壓發(fā)動(dòng)機(jī)在工作過程中燃料質(zhì)量流量特性對(duì)推力的穩(wěn)定性有顯著影響,通過燃面退移速率與燃燒室構(gòu)型的匹配,理論上可以構(gòu)造出使推力變化幅度較小的發(fā)動(dòng)機(jī)構(gòu)型。增大空氣流量更有利于固體超燃沖壓發(fā)動(dòng)機(jī)推力的穩(wěn)定。然而,影響推力的因素不僅僅為燃料質(zhì)量流量和空氣流量,燃燒室內(nèi)流場(chǎng)結(jié)構(gòu)同樣對(duì)其有影響。因此,文中僅從理論上對(duì)燃料質(zhì)量流量和空氣流量對(duì)固體超燃沖壓發(fā)動(dòng)機(jī)推力的影響有一個(gè)定性認(rèn)識(shí),即合適的燃面退移速率特性搭配合理的燃面構(gòu)型能夠讓固體燃料超燃沖壓發(fā)動(dòng)機(jī)在規(guī)定工作時(shí)間內(nèi)推力變化幅度較小,推力更加穩(wěn)定。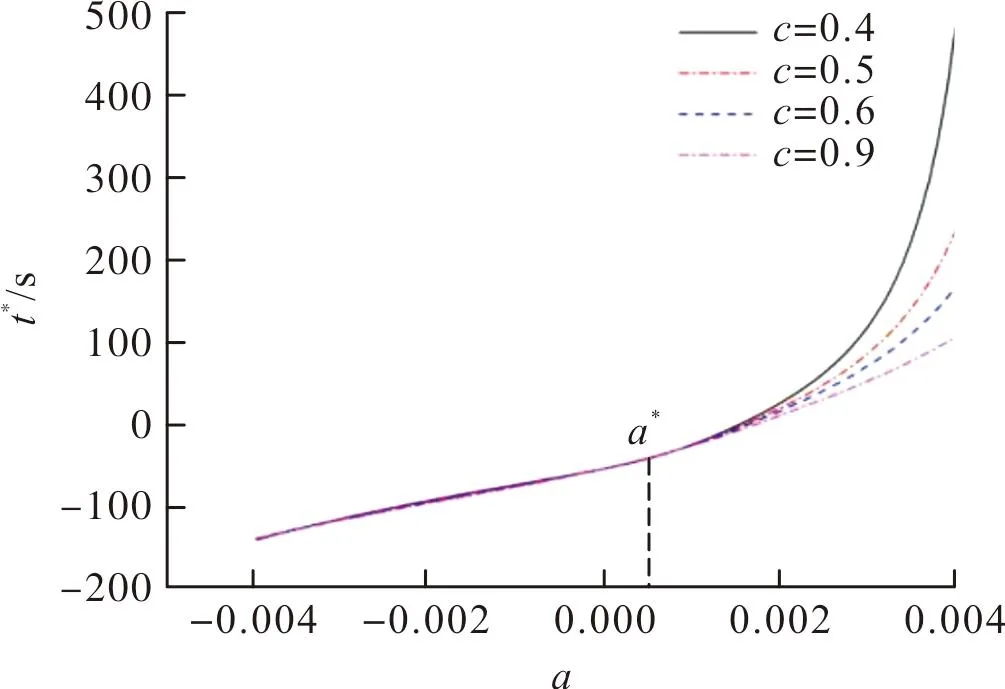
3 結(jié)論

