動靜態力共同作用對電抗器鐵心振動影響

閆榮格 程云飛

（1.省部共建電工裝備可靠性與智能化國家重點實驗室（河北工業大學） 天津 300130 2.河北工業大學河北省電磁場與電器可靠性重點實驗室 天津 300130）

0 引言

近年來，隨著大功率、高壓、超高壓輸電網的發展，根據電網負荷的變化而自動、快速、準確地進行無功功率調節十分重要，可控式并聯電抗器因其調節能力強而廣泛應用于其中，但在實際運行中會出現很嚴重的振動噪聲問題[1-4]。嚴重的振動噪聲不僅影響附近居民的生活，也會造成緊固件松動、影響電抗器的使用壽命等問題。目前，電抗器振動問題被廣泛關注，其研究具有現實意義。

許多學者對電抗器振動問題展開了廣泛研究。文獻[5]考慮了硅鋼片磁化與磁致伸縮特性的各向異性，分析了電磁應力對鐵心振動的影響。文獻[6-8]測量了諧波與直流偏磁條件下硅鋼片的磁特性，為進一步分析電抗器振動問題提供基礎。文獻[9]基于歷史聲振數據對電抗器運行狀態進行評估。

在實際工作時，電抗器鐵心會受到螺桿與夾件施加的靜態壓緊力作用，也會受到動態的磁致伸縮力與麥克斯韋力共同作用，動靜態力均會對硅鋼片磁特性產生影響，從而進一步影響電抗器鐵心電磁振動特性。文獻[10]通過制作的測試儀測量了單軸應力下硅鋼片的交變磁化特性，得出單軸應力不僅影響磁滯回線的形狀，也影響磁導率和損耗特性的結論。文獻[11]提出一種基于磁通密度線圈與磁感應強度線圈結合的測量結構，在二維旋轉磁化的過程中測量了壓應力與磁化性能的關系。文獻[12]測量了直流偏磁疊加應力情況下硅鋼片的磁特性，分析了磁致伸縮應力與麥克斯韋應力對電抗器振動特性的影響。文獻[13-15]利用測得的機械應力下磁特性曲線計算了電抗器不同位置的振動情況。文獻[16]研究了夾緊力對非晶合金材料的磁特性以及鐵心振動特性的影響，結果表明，非晶合金磁致伸縮效應隨夾緊力非線性變化，且非晶合金鐵心在沿著夾緊力方向隨夾緊力增加振動減弱顯著。文獻[17]通過施加螺桿壓緊力的方法抑制電抗器振動，結果表明，適當的預緊力有減振效果，當預緊力過大時，減振效果很差。

過去的研究均未考慮動態力對硅鋼片磁特性及鐵心振動的影響，也沒有考慮動靜態力共同作用的影響。因此，本文測量硅鋼片在動靜態力共同作用下的磁特性，建立電抗器電磁場-機械場雙向耦合模型，分析電抗器電磁振動特，進行電抗器振動測量實驗，對比實驗結果與理論分析結果，研究動靜態力對電抗器振動影響規律。

1 動靜態力條件下硅鋼片磁特性測量

電抗器鐵心電磁振動仿真計算時，硅鋼片磁特性數據對計算結果的準確性有直接影響。本次實驗采用愛潑斯坦方圈測量系統，該測量系統由25 cm標準愛潑斯坦方圈、AFG1022 型信號發生器、Model-MB500VI 型功率放大器、Model-50 型激振器、220V 調壓器、LC1004 型動態信號采集卡等組成。本次實驗中選用32 片硅鋼片作為試樣，采用雙搭接接頭的方式。該系統測量硅鋼片磁化特性的工作原理為：在交變磁場的作用下，硅鋼片被磁化，通過改變二次電壓的數值以調節磁感應強度，同時采集一次電流的數值來計算磁場強度，進而得到樣片的磁化曲線。磁致伸縮應變由動態信號采集卡、應變片和電橋測量與采集。當硅鋼片產生磁致伸縮應變時，應變片受應力彎曲，其阻值發生變化，通過轉換電路將阻值的變化轉換為電壓的變化，從而實現磁致伸縮應變的測量。本次實驗中測量了順磁化方向的磁致伸縮應變大小，其余兩個方向的磁致伸縮應變大小取該方向磁致伸縮應變數值的一半。硅鋼片磁特性曲線測量平臺如圖1 所示。

圖1 磁特性曲線測量平臺Fig.1 Magnetic characteristic curve measurement platform

試件的一側通過緊固螺桿固定，靜態壓緊力由另一側施壓螺桿施加，施加的壓緊力大小由壓力顯示屏顯示。動態力由信號發生器、功率放大器、激振器向樣片施加，動態力的合理模擬是本次實驗重點。電抗器鐵心振動可認為由動態的磁致伸縮力與麥克斯韋力共同激勵，因此在工頻交流電條件下動態力的變化趨勢為頻率100 Hz 的正弦曲線。在實驗中由信號發生器輸出頻率100 Hz 的正弦信號，該信號經功率放大器放大后輸入激振器，此時激振器的輸出便為正弦變化的激振力。方圈右側設置螺桿起緊固作用，動態激勵在左側施加，通過磁鐵將激振器輸出頂桿接頭與硅鋼片緊密連接，通過調節激振力的大小使待測樣品的振動情況與不同壓緊力條件下鐵心振動情況一致，激振力的大小可通過調節功率放大器供給的電流瞬時值來改變。

圖2 所示為同時考慮靜態壓緊力與動態振動力條件下硅鋼片磁化曲線。從圖2 中可以看出，靜態壓緊力的施加使硅鋼片磁化曲線右移，這是由于壓緊力的施加使硅鋼片內部磁疇偏轉更困難，隨著壓緊力的增大，硅鋼片工作點逐漸向右偏移，飽和磁感應強度逐漸下降。當考慮動態力的影響時，動態力的施加會使硅鋼片內部磁疇偏轉更活躍，硅鋼片工作點向左偏移，硅鋼片會更易被磁化，飽和磁感應強度升高，但隨著壓緊力的增大，動態力對硅鋼片磁化特性的影響逐漸變小。

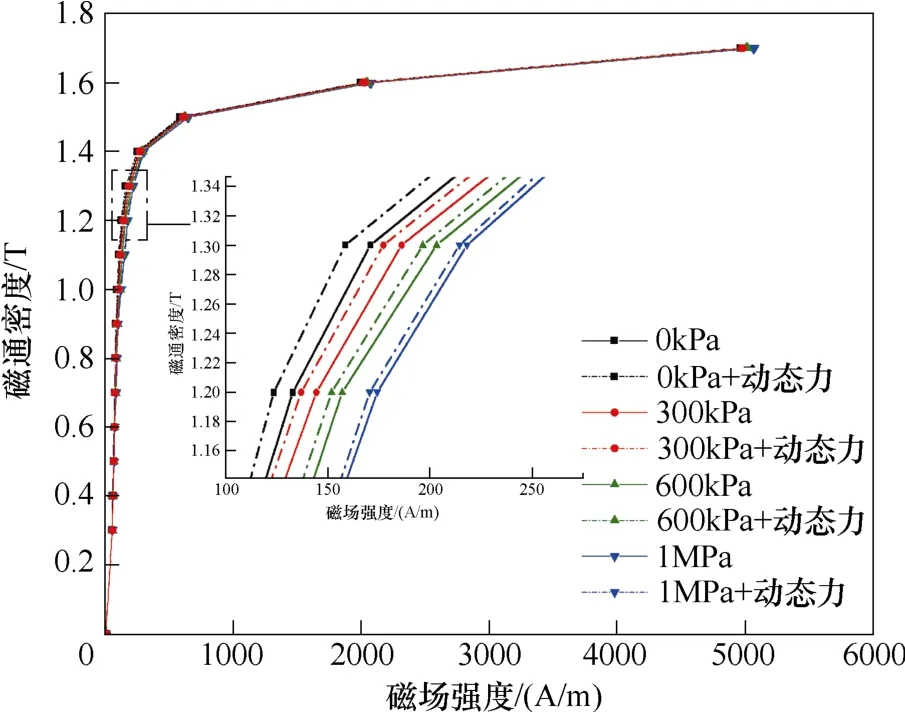
圖2 硅鋼片磁化曲線Fig.2 Magnetization curves of silicon steel sheet

圖3 所示為不同磁通密度、不同工況下的硅鋼片磁致伸縮特性測量曲線。施加的電壓激勵為50 Hz，在正弦電壓的一個周期內，磁致伸縮特性曲線出現兩個峰值，其周期近似為100 Hz，隨著磁通密度的增大，磁致伸縮現象加劇。以磁通密度1.6 T時不同工況下測量曲線為例，分析可知，當考慮靜態應力的影響時，靜態應力的施加使硅鋼片內部磁疇偏轉更困難，因此考慮靜態應力時磁致伸縮效應減弱。當考慮動靜態力共同作用的影響時，其磁致伸縮效應進一步減弱，這是因為施加的動態力為100 Hz 變化的力，這會引起一部分磁疇活躍，此時由磁致伸縮效應引起的磁疇偏轉較少，因此考慮動靜態力共同作用時磁致伸縮效應會減弱很多。

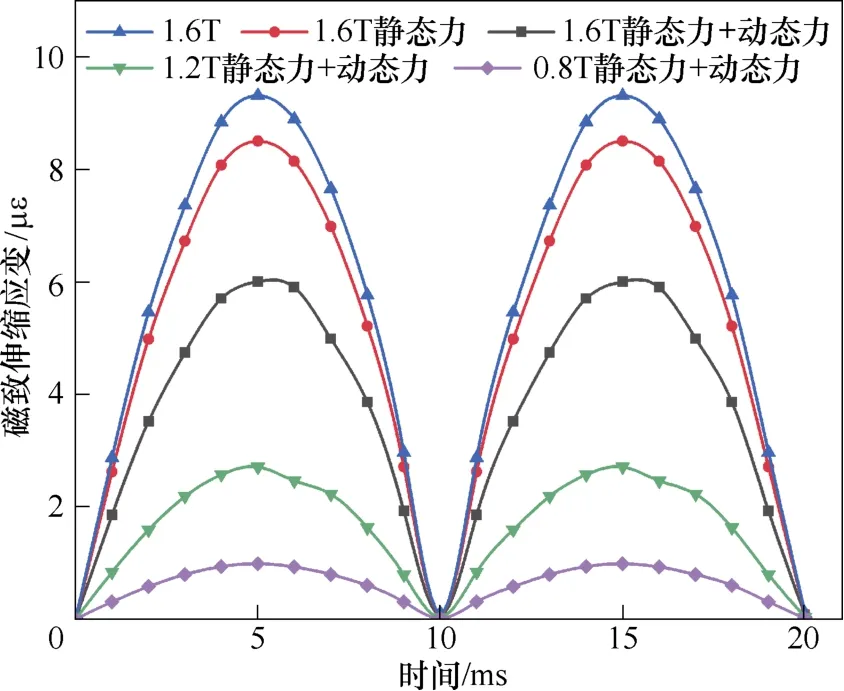
圖3 硅鋼片磁致伸縮曲線Fig.3 Magnetostrictive curves of silicon steel sheet

圖4 所示為考慮動靜態力共同作用影響時不同時間下的單值磁致伸縮插值曲線。在后文的電抗器電磁振動計算中，并非采用單一的磁致伸縮峰值插值曲線，在每個時間步的計算中使用對應的磁致伸縮單值插值曲線，一方面更符合實際工況；另一方面可以更方便地在不同時間下根據動靜態力更新磁特性曲線，使計算結果更加精確。

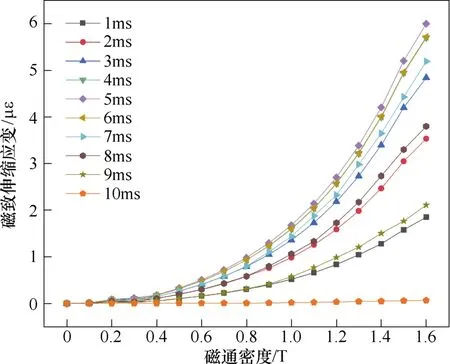
圖4 不同時間下磁致伸縮單值插值曲線Fig.4 Magnetostrictive single-valued interpolation curves at different times

根據磁致伸縮特性測量結果，磁致伸縮系數d可看作為隨時間變化的量，其可寫為

式中，ω為基波角頻率；n為諧波次數；Nh為計算中截斷諧波的次數；df,n為d(t)的第n次諧波分量。

綜上所述，靜態壓緊力與動態振動力均會影響硅鋼片磁特性，進一步對電抗器鐵心電磁振動產生影響，因此在對電抗器進行電磁振動計算時應考慮這部分影響。

2 電磁場-機械雙向耦合模型

2.1 磁致伸縮效應

磁致伸縮效應是電抗器振動的原因之一。磁致伸縮效應僅在磁場施加時產生，去掉磁場后，磁致伸縮效應消失。因此可應用彈性力學的關系等效磁致伸縮應力，三維彈性體的應力應變關系可寫為

式中，σms為等效磁致伸縮應力矩陣；ε為磁致伸縮應變矩陣；D為彈性張量矩陣，可寫為

式中，E為材料楊氏模量；α為材料泊松比；Y與Z分別為

式中，E為三階單位矩陣。根據虛位移原理，可將單元節點的磁致伸縮力等效為

2.2 麥克斯韋力

帶氣隙結構的電抗器，在氣隙區域存在麥克斯韋力，麥克斯韋應力張量是一個多重方向性的張量，麥克斯韋力Fmw可由應力張量T的面積分計算。

式中，Bx、By、Bz分別為磁通密度在x、y、z方向上的分量；Hx、Hy、Hz分別為磁場強度在x、y、z方向上的分量；nx、ny、nz為方向矢量。

鐵心內部麥克斯韋電磁力隨時間周期性變化，當考慮靜態壓緊力與動態力對硅鋼片磁化特性的影響時，硅鋼片磁化特性的變化會對麥克斯韋力的計算產生影響。

2.3 電磁場-機械雙向耦合模型

考慮動靜態力共同影響時，電抗器系統能量包含磁場能、電流位能、應變能、磁彈性能、磁邊界上的位能、外力位能、磁致伸縮力位能與麥克斯韋力位能，其能量泛函可寫為

式中，Ω1、Ω2分別為機械場和磁場的分析域；Γ1、Γ2分別為機械場Ω1和磁場Ω2的邊界；A為矢量磁位；B為磁通密度；H為磁場強度；J為電流密度；u為位移矢量；fΓ為外表面力密度；fΩ為外體積力密度。

由于A、B、H、J、u、Fms、Fmw這些變量是時間性的周期變量，因此可由復數形式表示為

式中，Af,n、Bf,n、Hf,n、Jf,n、uf,n、Fmsf,n、Fmwf,n分別為A(t)、B(t)、H(t)、J(t)、u(t)、Fms(t)、Fmw(t)的第n次諧波分量。

在三維對稱場中只存在第一類邊界條件，因此磁邊界上的位能為零，將能量泛函中各項按直角坐標系展開，磁場能為

電流位能為

應變能為

磁彈性能為

靜態力位能為

磁致伸縮力位能與麥克斯韋力位能可寫為

在對三維軸對稱場離散時，采用四面體單元，以磁場離散為例，設四面體四個頂點對應的磁矢位函數AK、AM、AN、AL，則四面體單元內任意一點磁矢位函數均可由線性插值函數逼近，可寫為

式中，V為四面體單元體積，位移場離散同理。為了進行單元變分計算，將能量泛函定義到單元區域內，即，e為單元總數，由于磁矢位與位移矢量均已離散到各個節點上，因此能量泛函I可寫為關于磁矢位A和位移矢量u的函數，將泛函變分問題轉換為多元函數求極值問題，能量泛函I對每一個節點上磁矢位分量與位移矢量分量的偏導數都為零，可表示為

可將方程寫成矩陣形式為

式中，S為電磁剛度矩陣；K為機械剛度矩陣；S與K中的每一個元素都是常數，可看作與時間無關的線性項；X為位移矢量矩陣；F為由外體積力、外表面力、磁致伸縮力、麥克斯韋力組成的列矩陣。

圖5 所示為并聯電抗器電磁機械場雙向耦合計算流程，在每個時間步下選用對應的磁特性曲線，對建立的鐵心模型進行電磁振動計算。考慮動靜態力共同作用對硅鋼片磁特性的影響時，根據不同的實際工況更新硅鋼片磁特性曲線重新進行計算，當兩次迭代的計算結果小于設定誤差時，模型收斂滿足條件，輸出計算結果。

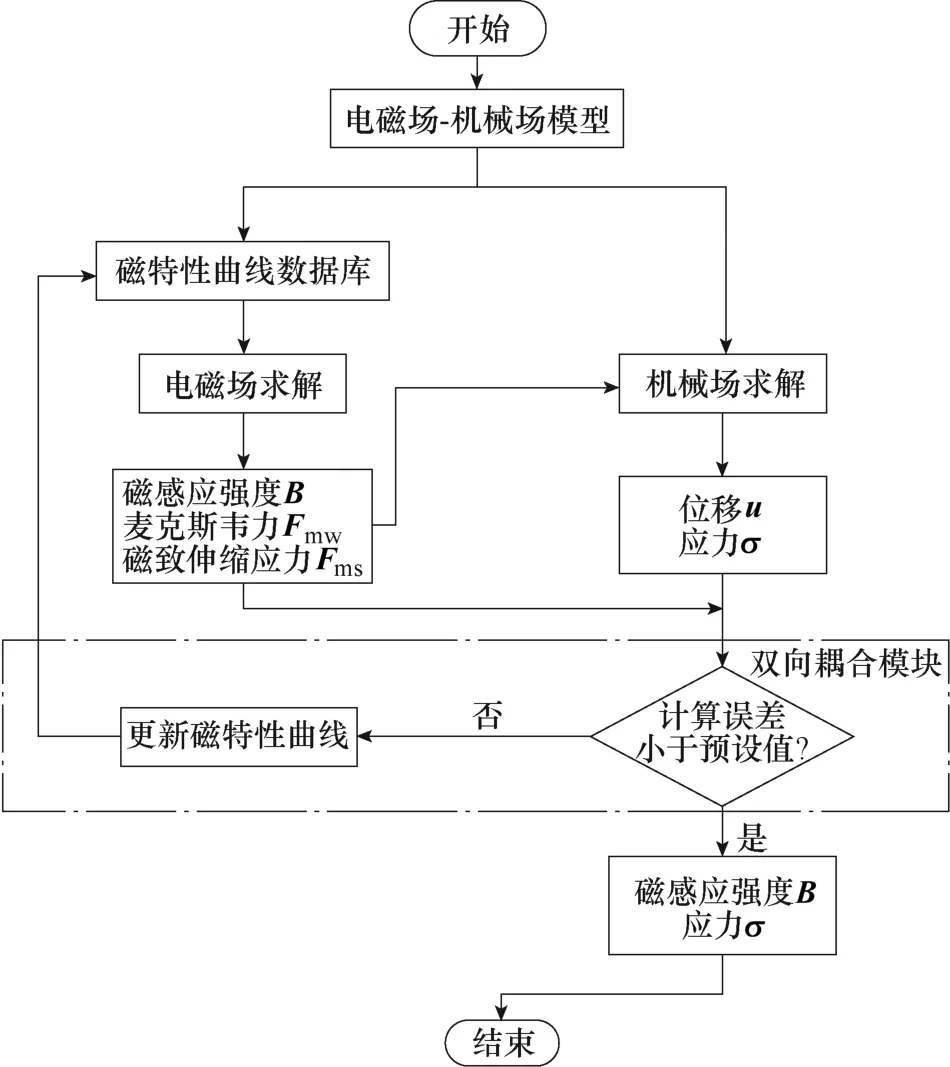
圖5 并聯電抗器雙向耦合計算流程Fig.5 Flow chart of two-way coupling calculation of shunt reactor

3 仿真與實驗分析

根據建立的電抗器電磁場-機械場耦合模型，可對電抗器鐵心進行電磁振動計算，仿真中并聯電抗器鐵心尺寸為190 mm×170 mm×40 mm，3 個鐵心柱寬為40 mm，關于中線對稱開有兩個寬35 mm 窗口，窗口高度為90 mm，每個鐵心柱中間開有2 mm 的氣隙，氣隙處填充環氧樹脂墊塊。左右兩側為交流繞組，交流繞組匝數為200 匝，中間為直流控制繞組，直流繞組匝數500 匝，并聯電抗器鐵心模型如圖6所示。計算中，將鐵心分為兩部分，受到靜態壓緊力與動態振動力影響的鐵軛部分和僅受到動態振動力影響的鐵心柱部分，分別在鐵軛部分與鐵心柱部分取測點A、B。

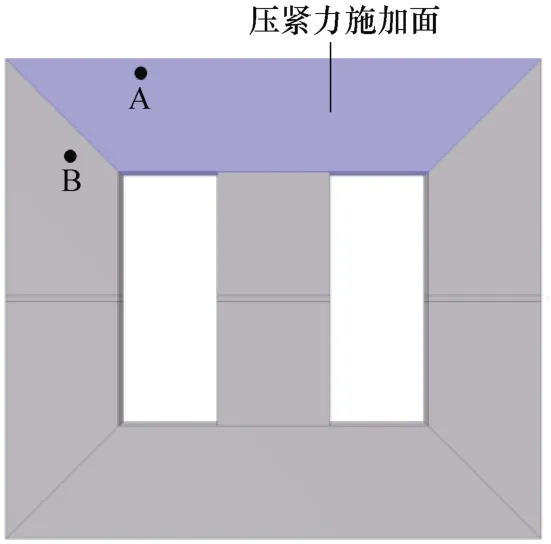
圖6 并聯電抗器鐵心模型Fig.6 Shunt reactor core model

3.1 磁場、應力分析

根據測量的磁特性曲線，利用仿真軟件對并聯電抗器進行電磁振動計算，t=0.005 s 時刻電抗器鐵心磁通密度、應力分布如圖7 所示。

由圖7 分析可知，鐵心中間直流柱磁通密度較小，兩側交流柱磁通密度較大，鐵心拐角處為磁通密度集中分布區。由于設置了底部約束，因此應力集中分布于下鐵軛處，鐵心拐角處同樣出現應力集中分布區。

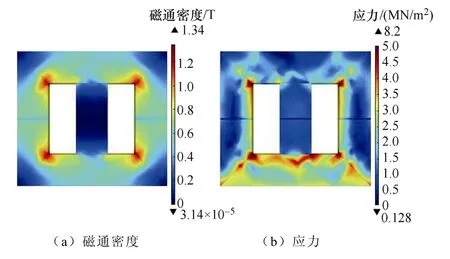
圖7 鐵心磁通密度、應力分布Fig.7 Core magnetic density distribution

電抗器鐵心振動可近似認為由磁致伸縮應力與麥克斯韋應力共同激勵，首先定量計算磁致伸縮應力與麥克斯韋應力，進一步分析其對振動的影響，測點B 應力曲線如圖8 所示。分析可知，磁致伸縮應力與麥克斯韋應力均為100 Hz 變化的正弦曲線。對于并聯電抗器，磁致伸縮應力數值較麥克斯韋應力數值小很多，因此并聯電抗器鐵心振動主要由麥克斯韋應力引起。總應力的數值小于麥克斯韋應力，這是由于鐵心材料硅鋼片的磁致伸縮效應是正效應，而鐵心餅間麥克斯韋力可看作電磁吸力，其方向在空間上與磁致伸縮效應相反，二者有一定的“相消”作用，因此總應力的數值會較麥克斯韋應力的數值小，磁致伸縮應力與麥克斯韋應力在空間上呈一定的電角度，二者并不是直接相減的關系。

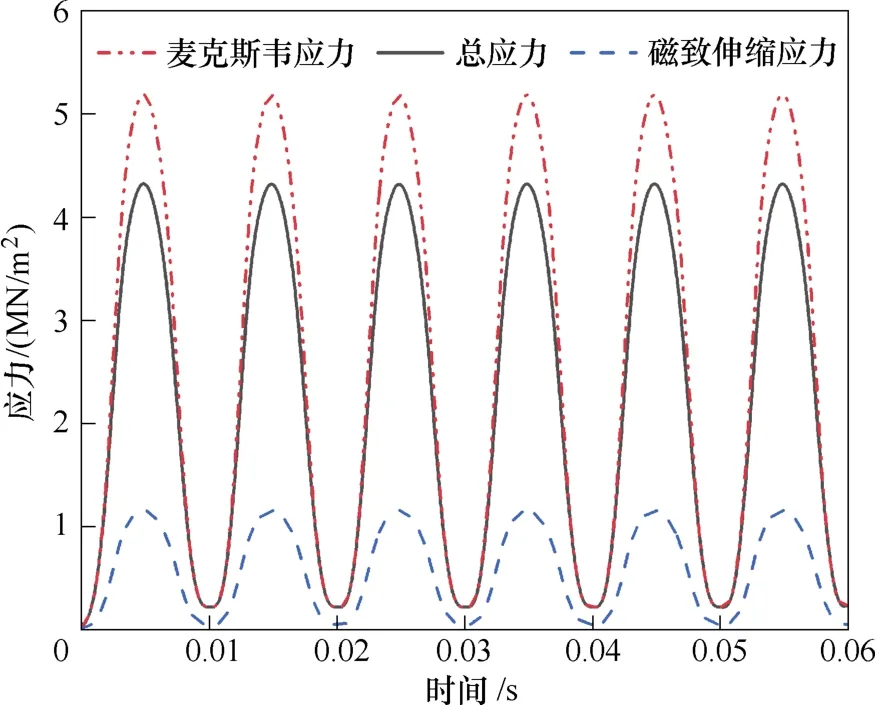
圖8 測點B 應力曲線Fig.8 Stress curves of measuring point B

由于麥克斯韋應力是并聯電抗器振動的主要原因，當考慮動靜態力共同作用對硅鋼片磁特性的影響時，變化的磁特性影響了麥克斯韋應力的分布，從而影響了鐵心應力分布，進一步影響了鐵心振動情況。

為了更直觀地分析動靜態力對鐵心磁通密度、應力分布的影響，對兩代表性測點A、B 進行分析，結果如圖9 所示。對于鐵軛處測點A，其同時受到壓緊力與動態力作用，隨著壓緊力的增加，磁通密度計算值減小。由于該部分直接受到外部施加壓緊力的影響，因此應力的計算值會隨施加壓緊力的增大而增大。考慮動態力對硅鋼片磁特性的影響時，硅鋼片磁化工作點左移，飽和磁感應強度增大，因此磁通密度、應力的計算值有所增大，隨著壓緊力的增大，動態力對硅鋼片磁特性的影響逐漸減小，其對磁通密度、應力計算值的影響也逐漸減小。對于鐵心柱處測點B，其不直接受到壓緊力的作用，但壓緊力的施加對鐵心整體的磁通密度、應力分布均有影響，磁通密度、應力的計算受壓緊力的影響基本呈線性變化。外部施加壓緊力相同條件下，考慮動態力對硅鋼片磁特性的影響時鐵心飽和程度較高，測點B 磁通密度、應力的計算值也有所增大。對于高磁通密度區測點B，其磁通密度、應力計算數值受動態力影響較大，根據第1 節磁化曲線測量的結果可知，動態力對硅鋼片磁化特性的影響主要集中于0.9 T 以上的高磁通密度區，因此在鐵心高磁通密度區的數值計算結果會受動態力影響較大。

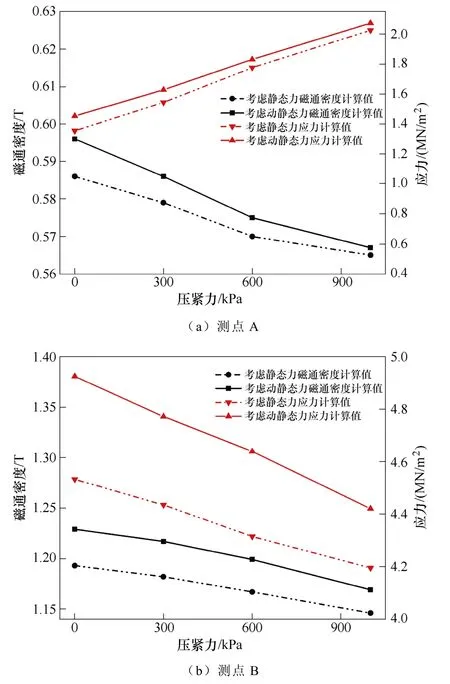
圖9 磁通密度、應力比較Fig.9 Magnetic density and stress comparison

3.2 振動分析

采用第2 節建立的耦合模型進行計算，如圖10所示為測點A、B 的加速度曲線，分析可知，各方向加速度曲線均為100 Hz 變化的正弦曲線。對于測點A，壓緊力沿著y軸方向施加，其應對y方向加速度計算數值影響較大，但y方向加速度計算數值較小，其對電抗器振動影響不大，因此僅考慮壓緊力對x、z方向振動的影響，隨著壓緊力的增加，x、z方向加速度數值不同程度地下降。對于測點B，其位于鐵心拐角處高磁通密度區，因此振動情況較測點A 劇烈。

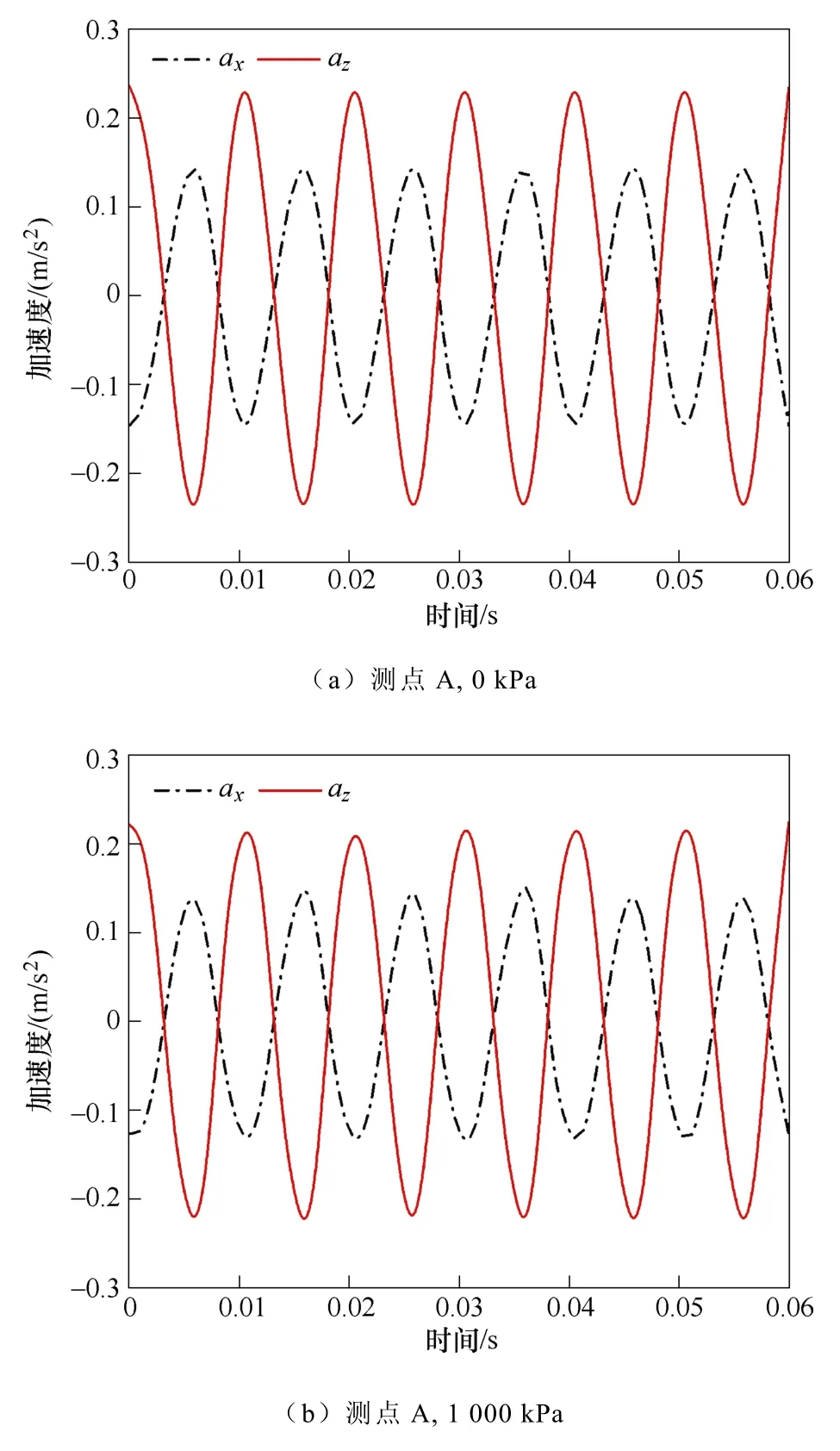
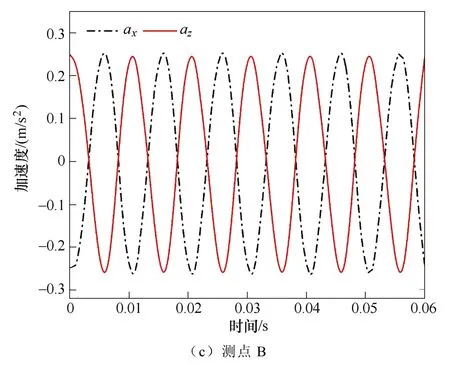
圖10 不同測點加速度曲線Fig.10 Acceleration curves of different measuring points

3.3 實驗驗證

為了對仿真模型進行驗證，對并聯電抗器進行不同壓緊力下振動特性實驗。振動實驗測量系統由220V 調壓器、PC、并聯電抗器、加速度傳感器、Squadriga_II 振動測試儀組成。調壓器輸出工頻交流電，加速度傳感器通過蜜蠟粘至測點，測量的振動信號通過振動測試儀傳至 PC，測量平臺如圖11 所示。

圖11 振動測量系統Fig.11 Vibration measurement system

測點A 實驗加速度曲線如圖12 所示。從圖中可以看出，實驗與仿真存在誤差，產生誤差的原因可歸結為以下幾個方面：①在仿真過程中對電抗器設置為底部約束，但是在實際實驗過程中，電抗器很難實現效果很好的底部約束效果；②實驗中外界環境的干擾與其他設備的運行也會使實驗結果出現誤差；③仿真過程中僅采用硅鋼片的磁測量數據，不能很好地模擬疊片鐵心的效果。由圖12 可知，y方向加速度數值較小，其對鐵心振動影響不大，隨著壓緊力的增加，x、z方向加速度幅值不同程度下降。總體來說，實驗值與仿真值波形趨勢一致，幅值存在一定的誤差，但誤差也在接受范圍內，證明了建模的合理性，也證明了理論分析的正確性。

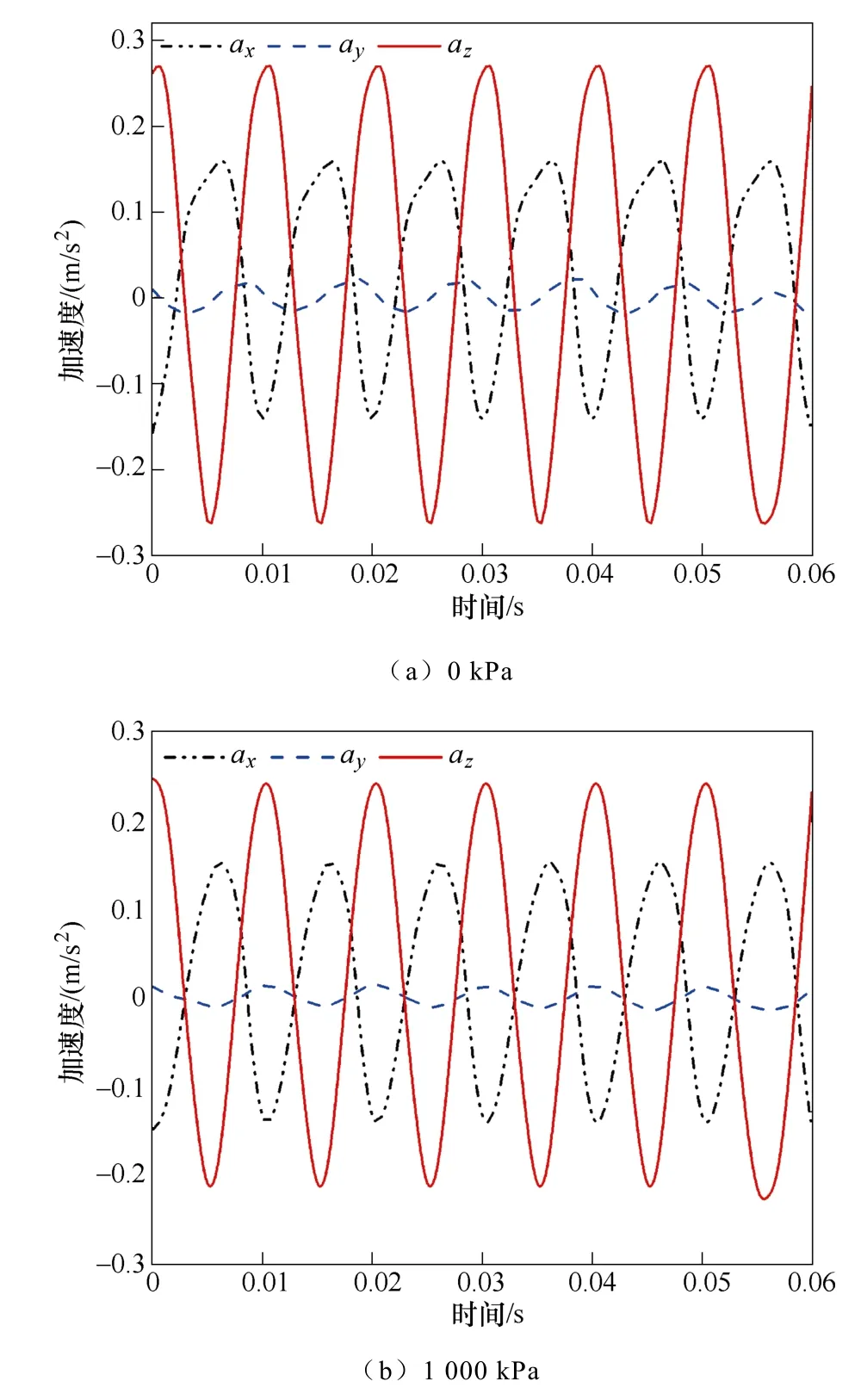
圖12 測點A 實驗加速度曲線Fig.12 Experimental acceleration curves of measuring point A

為了更直觀地分析考慮動靜態力對鐵心振動的影響，采用加速度峰峰值表征鐵心振動情況，將實驗測量的數據與仿真計算的數據進行對比，得到的結果見表1。

由表1 數據分析可知，靜態壓緊力對x方向加速度影響較小，z方向加速度影響較大。圖13 所示為不同條件下加速度計算值對比，當僅考慮靜態壓緊力的影響時，加速度計算值隨壓緊力的增加而減小。當考慮動靜態力共同作用對硅鋼片磁特性影響時，加速度計算數值較僅考慮壓緊力時有所增大。動態力影響硅鋼片磁致伸縮效應，使其數值下降很多，但由3.1 節分析可知，磁致伸縮應力對電抗器振動影響較小，麥克斯韋力是并聯電抗器振動的主要原因，因此動態力對硅鋼片磁化特性的影響才是影響電抗器振動的關鍵因素，動態力使硅鋼片飽和磁感應強度升高，變化的磁特性影響了麥克斯韋力的計算，在機械場計算中又將麥克斯韋力作為激勵施加，因此改變了振動計算的結果。無壓緊力時動態力對加速度計算數值影響較大，隨著壓緊力的增加，動態力對加速度計算影響程度下降。當考慮動靜態力共同作用對硅鋼片磁特性的影響時，其振動計算精度高于僅考慮靜態力影響時振動計算精度，證明了考慮動靜態力共同作用時電抗器建模的合理性與精準性。

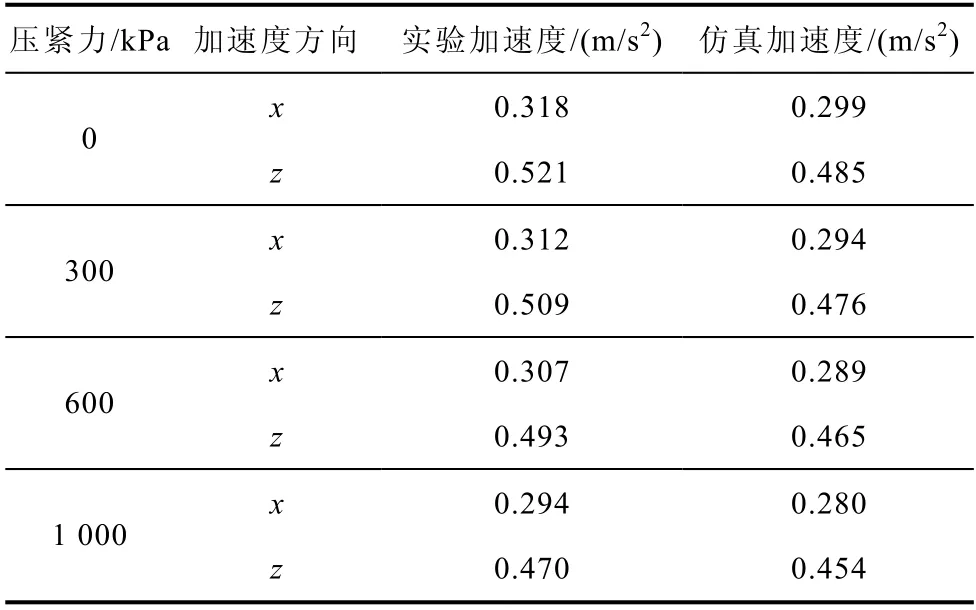
表1 實驗與仿真加速度峰峰值對比Tab.1 Experiment and simulation acceleration peak-to-peak comparison

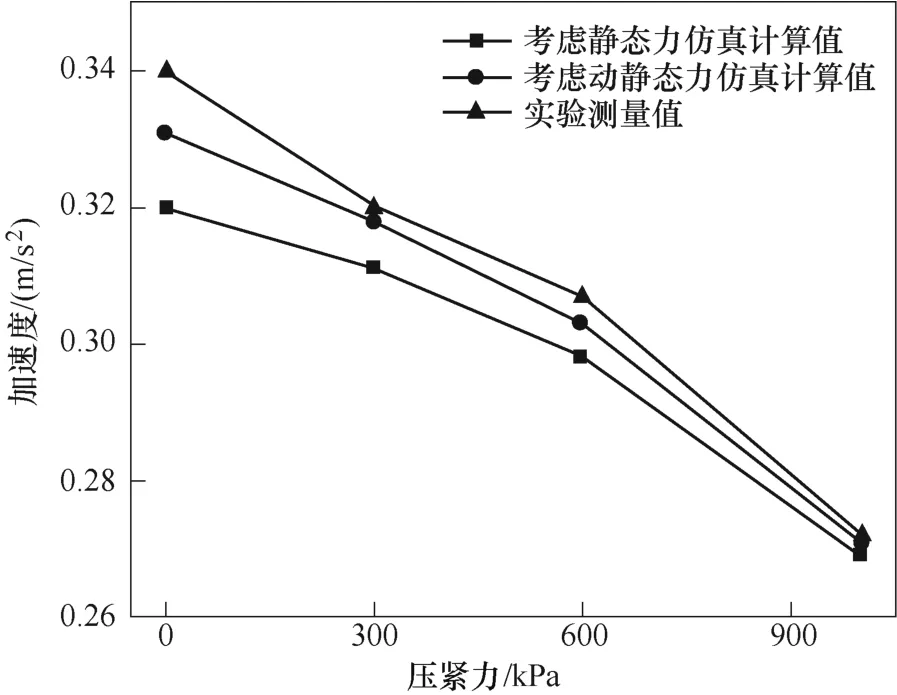
圖13 加速度對比Fig.13 Acceleration comparison chart

為了進一步對電抗器振動情況進行分析，將加速度曲線轉換成頻譜圖，結果如圖14 所示。

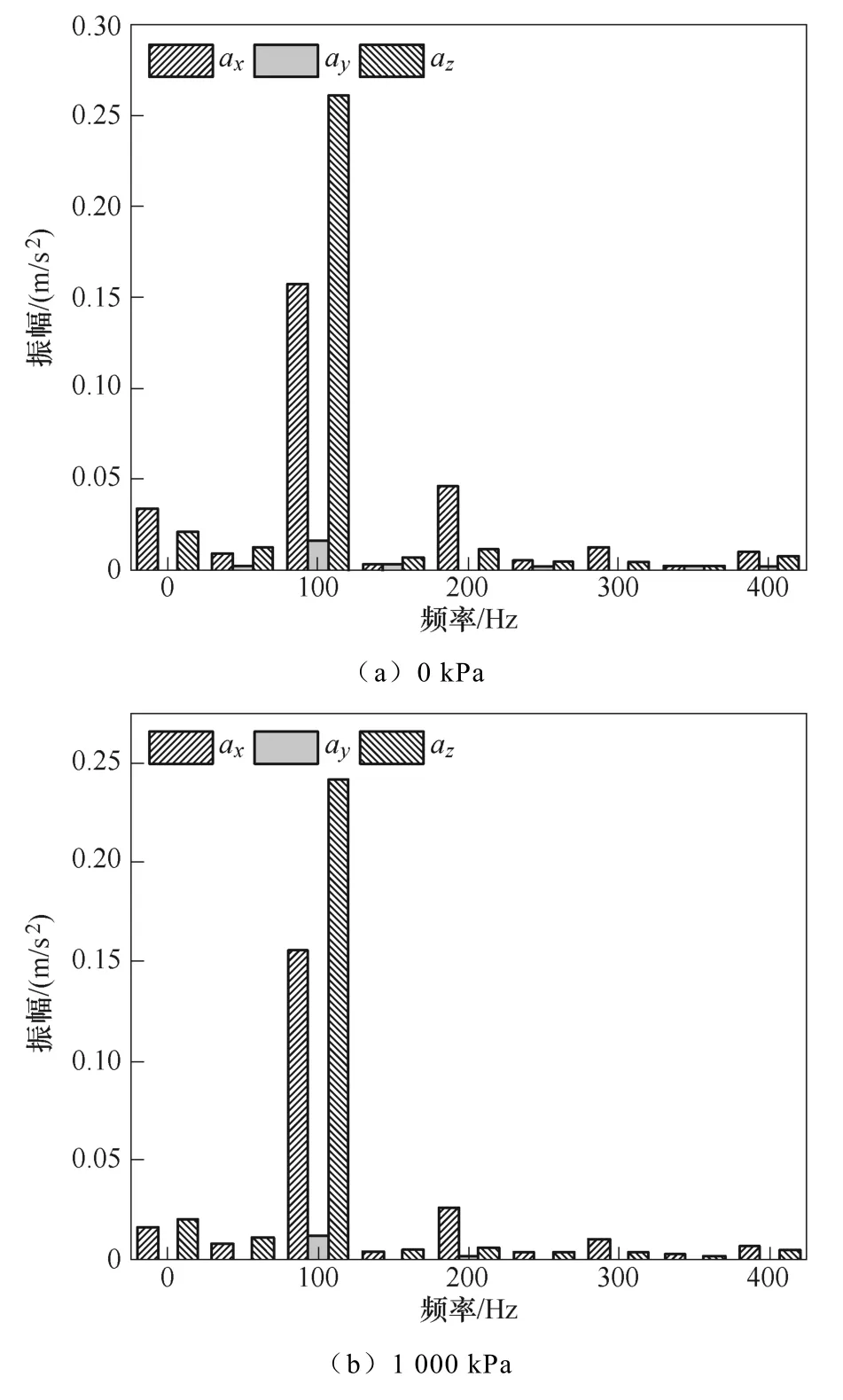
圖14 測點A 實驗加速度頻譜圖Fig.14 Acceleration spectrogram of measuring point A

由圖14 的頻譜圖分析可知，壓緊力的施加僅影響加速度各頻率分量的幅值，并不在振動中產生新的諧波分量。工頻交流電條件下，100 Hz 分量占振動信號的主要分量，這是由于鐵心的磁致伸縮效應與鐵心餅間的麥克斯韋力是鐵心振動的主要原因，并聯電抗器工作于工頻下，麥克斯韋力與磁通密度的二次方成正比，磁致伸縮效應基本正比于磁通密度的二次方，因此此時電抗器的振動主頻率為100 Hz，其余振動分量分布于100 Hz 的整數倍。這也驗證了第1 節在考慮動、靜態力共同作用的硅鋼片磁特性實驗中施加頻率100 Hz 動態激勵的正確性。

4 結論

本文在考慮動靜態力共同作用對硅鋼片磁特性影響的基礎上，建立并聯電抗器電磁場-機械場雙向耦合模型，分析電抗器鐵心電磁振動特性，通過仿真與實驗相結合，分析結果如下：

1）搭建硅鋼片磁特性測量平臺，測量了考慮動靜態力共同作用下硅鋼片的磁化特性與磁致伸縮特性。僅考慮靜態壓緊力影響時，磁導率減小，磁致伸縮效應減弱；考慮動靜態力共同影響時，磁導率較僅考慮靜態壓緊力影響時增大，磁致伸縮效應進一步減弱。

2）建立并聯電抗器電磁場-機械場雙向耦合模型，對并聯電抗器鐵心進行電磁振動計算，分析了動靜態應力對電抗器鐵心電磁振動的影響。

3）搭建振動測量實驗平臺，對考慮動靜態力共同作用影響的并聯電抗器電磁場-機械場雙向耦合模型進行實驗驗證，實驗結果表明，加速度的波形與幅值誤差均在合理的范圍內，考慮動靜態力共同作用的影響時振動計算誤差更小，證明了建模的正確性與精準性，其可為電抗器振動問題進一步研究提供理論指導。