基于項目作答反應時間的作弊甄別研究進展

楊志明 徐慶樹

(湖南師范大學外國語學院,長沙 410081)

1 引言

作弊甄別研究一直是考試研究的重點課題,考試中的作弊現象不僅干擾了考試秩序(胡佳琪 等,2020;駱方 等,2020),影響了考試的信效度,影響評分標準或合格線劃定(Sinharay,2021),而且違反國家有關考試的法律法規(Crittenden,Hanna,& Peterson,2009;彭恒利,2015)。一直以來,大量的研究者采用心理計量學、統計學的研究方法甄別各種作弊現象(Cizek &Wollack,2017;Sinharay,2017;van der Linden &Lewis,2015)。近年來,隨著基于計算機的測試(computer based test,CBT)的快速發展,考生在考試中的項目作答反應時間可以被搜集、記錄、使用(Zopluoglu,2019)。正如van der Linden所說,項目作答反應時間一直以來都被看作是識別個人行為的重要信息源,但只在基于計算機的測試普及后,這一信息源才能得到解碼使用(van der Linden,2006)。

最近10年間,越來越多的研究者開始嘗試使用考生的項目作答反應時間甄別考生的異常作答情況(Man &Harring,2021;Nagy &Ulitzsch,2021)。然而,本研究發現國外研究者應用此類方法較多,而國內研究者應用此類方法較少。為更好的介紹這種作弊甄別方法,本文首先對考試作弊現象進行界定與分類,接著介紹基于項目作答反應時間建模的研究假設、建模方法和個人數據擬合方法,然后進一步闡釋各類建模方法、擬合方法在不同類型作弊行為甄別中的應用和實踐,最后對這種作弊甄別方法中存在的相關問題開展總結和討論。

2 考試作弊現象的界定與分類

考試作弊呈多發態勢(彭恒利,2015),作弊形式趨于多樣化,作弊工具趨于高科技化、作弊行為向團伙化、集團化、專業化方向發展,考試作弊逐漸形成產業鏈,向商業化運作模式轉變。面對當前紛繁復雜的作弊現象,沒有任何一種研究方法或者統計模型可以全部適用。因此,開展考試作弊現象研究,首先要對考試作弊行為進行界定、分類(Sinharay,2020)。

基于作弊主體的分類較多。有研究者基于作弊主體的規模將作弊行為分為個人作弊行為和團體作弊行為(胡佳琪 等,2020;駱方 等,2020)。我國政府對作弊行為進行的分類主要也是基于作弊主體開展的。教育部頒布的《國家教育考試違規處理辦法》界定了3類作弊行為,分別是:考生的作弊行為、考試工作人員的作弊行為、組織作弊的行為。《刑法修正案(九)》按作弊主體分別做出作弊犯罪的處罰規定,其中對組織作弊者的處罰規定為:“在法律規定的國家考試中,組織作弊的,處三年以下有期徒刑或者拘役,并處或者單處罰金;情節嚴重的,處三年以上七年以下有期徒刑,并處罰金。”

當然,也有研究者基于作弊行為的分布特點、動機和發生場景進行了分類。Cizek提出3大類59種作弊行為,其中最常見的是抄襲(Cizek,1999)。從作弊動機的角度,Cizek進一步將作弊行為分為2類:一類是考試欺詐(test cheating),主要指需要參加考試并獲得成績的個人或者群體進行的作弊行為;另一類是考試盜竊(test theft),主要指作弊者無需參加考試、從考試作弊中牟利的行為(Cizek &Wollack,2017)。Wollack等按照作弊發生的場景將作弊行為分為3類:第一類是答案抄襲與共謀作弊(answer-copying and collusion),指的是作弊考生單獨或與其他考生協作,進行答案抄襲的現象;第二類是泄題(item preknowledge),指的是考生通過各種手段在交卷前獲取考試的項目信息現象;第三類是篡改答案(test tampering),指的是考生、教師、考試機構工作人員等通過修改考生答案的方式進行的作弊行為(Wollack &Fremer,2013)。

本研究在前述作弊分類方案的基礎上進行總結,提出“兩種三類”的作弊行為分類方法:“兩種”指的是作弊主體,也就是:個人作弊、團體作弊,兩種作弊行為;“三類”則分別指的是:泄題、抄襲和篡改答案。

3 基于項目作答反應時間的作弊甄別方法

基于項目作答反應時間的作弊甄別方法基本可以分為2類:一類是參數法,一類是非參數法。參數法的基本假設為:假定項目作答反應時間是一個連續變量,該變量的分布規律符合某種特定分布,如對數正態分布(lognormal distribution)(van der Linden,2006;van der Linden,2008;van der Linden,2009)、伽馬分布(gamma distribution)(Verhelst,Verstralen,& Jansen,1997)、指數分布(exponential distribution)(Scheiblechner,1979,1985)、偏正態分布(孟祥斌,2016)等,研究者基于項目作答反應時間的這種分布特點構建模型。在個人數據擬合中,研究者再將模型的預測值與實際觀測值進行比較,如果二者相差過大,就懷疑考生或有作弊、試題或被泄露(Qian,Staniewska,Reckase,& Woo,2016;van der Linden &Guo,2008)。非參數法則另做假定:考生的項目作答反應時間是一個離散變量,單個題項的項目作答反應時間的分布可以和考生總體的項目作答反應時間進行對比。基于這種假設,研究者就可省去參數建模的步驟,直接采用如KL離散度等方法比較考生個體和考生群體的作答反應時間模式,進行作弊甄別,也取得了不錯的效果(Man,Harring,Ouyang,& Thomas,2018)。

3.1 參數建模法

參數建模法主要有3類參數模型:一是基于作答反應時間的模型,這類模型以對數正態模型應用最為廣泛;二是基于項目作答反應時間和作答正誤情況聯合建模的層次框架模型;三是在第二類模型基礎上增加眼動等其他過程數據的聯合建模。

3.1.1 對數正態模型

van der Linden(2006)采用對數正態模型對考試中的項目作答反應時間進行建模,這種建模方法擬合優度較高,獲得了廣泛認可。此方法假定考試中的項目作答反應時間具有隨機性,且呈對數正態分布(lognormal distribution),因此借鑒項目反應理論的兩參數模型的建模方法,提出項目作答反應時間的對數正態分布模型(Lognormal Model),構建考生做題速度參數τ、題項參數βi、αi,用以擬合考生作答反應時間的分布情況,公式如下:

f(ti;τ,αi,βi)=

(1)

其中,ti代表考生t在進行題項i作答時所用的時間,τ則代表了考生的做題速度,τ取值越大,則考生在該題項上花費的時間越少。βi則代表了試題的時間消耗度(time intensity),βi的取值越大,考生在該試題上花費的時間就越多。而αi如同在項目反應理論中一樣,是一個作答時間區分度指標,取值大于0,且取值越大,考生在第i個題的作答時間的對數分布越集中;取值越小,則越分散。因此,αi這一指標可以實現以題項為單位區分做題速度不同的考生。

模型背后的原理可以對照對數正態模型的公式(公式2)進行解讀:

f(x,μ,σ)=

(2)

對照可知,項目作答反應時間對數正態分布模型的均值和標準差分別為:

μi=βi-τ,

(3)

(4)

公式1中的ti(考生t在第i題的做題時間)的對數lnti服從正態分布:其均值由題項的時間消耗度βi和考生的做題速度τ決定(公式3);標準差為試題的作答時間區分度αi的倒數(公式4)。

為了提高模型的可識別性,van der Linden(2006)對公式1中提到的變量進行了約束。速度參數τ,應該符合公式5:

(5)

也就是說,第j個人的做題速度可以取正值或者負值,所有人的做題速度之和等于0。

結合公式3可知,第j個考生在第i個題項上的作答反應時間的對數分布模型的均值等與第i個題項的時間消耗度βi減去第j個考生的做題速度τj,公式如下:

βi-τj=μij,

(6)

由此可知:

(7)

套入公式5的約束,可以得到:

(8)

這就是說試卷中所有試題的時間消耗度的均值等于所有考生作答所有題目所需的項目反應時間的對數正態分布的均值。

van der Linden(2006)認為可以采用MCMC方法(吉布斯采樣)對這個模型進行參數估計。但是,同項目反應理論一樣,在參數估計前需要先進行局部獨立性假設:一是,考生個體之間具有局部獨立性;二是,給定考生作答所有試題的項目作答反應時間之間具有局部獨立性。在此基礎上,考生的參數τj符合正態分布:

(9)

同時,他指定試題參數作答時間區分度αi服伽馬分布(公式10),題項時間消耗度βi服從正態分布(公式11):

(10)

(11)

如公式11所示,βi的正態分布標準差中含有參數αi,且αi服從gamma分布,因此,(βi,αi)服從normal-gamma分布。

在Gibbs采樣中,交替給定考生參數τ和試題參數(α,β)按照公式(12)進行參數估計:

(12)

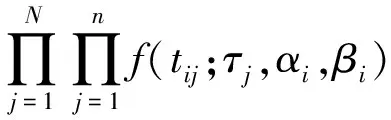
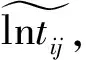
3.1.2 層次框架模型

van der Linden(2009)提出考生在作答速度和作答正誤情況之間會做出權衡(speed-accuracy tradeoff),并提供示意圖:

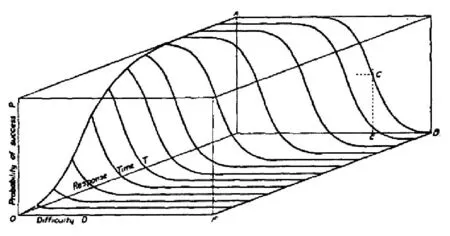
圖1 瑟斯多恩作答反應面示意圖(Thurstone’s response surface)

圖中橫軸為試題難度、縱軸為作答時間、豎軸為作答正確率,圖示作答時間越長,正確率越高。很多研究者基于此開展項目作答反應時間和項目作答正誤情況的聯合建模分析。De Boeck 和 Jeon(2019)認為這種聯合建模一般可以分為四類:第一類是將項目作答反應時間作為因變量,將做題正誤情況作為自變量的建模(Thissen,1983);第二類則是將項目作答正誤情況作為因變量而將項目作答反應時間作為自變量的建模(Roskam,1987;Verhelst et al.,1997);第三類則是將項目作答反應時間和項目作答正誤情況同時作為因變量且二者之間無因果關系的建模分析van der Linden(2007);第四類則是將項目作答反應時間和項目作答正誤情況同時作為因變量且將二者之間的因果關系也考慮到數據模型中的建模方法(dependency model,本文譯作“依存模型”)(Bolsinova &Maris,2016)。在所有這些模型中,van der Linden(2007)提出的層次框架模型是使用最多且最為廣泛的模型,本文重點介紹這一模型。

作答反應時間經常和考生的準確率一起聯合建模。這種建模方式的基本假設是:考生可以選擇高準確率低速度答題,也可以選擇低準確率高速度答題,其中速度是自變量,而準確率是因變量。根據項目反應理論,我們可以估計出能力值θ。在此基礎上,van der Linden(2007)基于作答反應時間和考生的準確率進行聯合建模,提出了層次框架模型。這種建模方式主要基于以下5個關鍵假設:一是個體考生的做題速度相對固定;二是個體考生在作答單個題項時,其做題速度和作答對錯情況均屬于隨機變量;三是題項的參數(如時間消耗度、時間區分度、難度、區分度)和考生參數(做題速度、能力值)等可以分開計算;四是在給定做題速度和做題能力的前提下,作答對錯和項目反應時間之間條件獨立;五是可以用樣本考生的數據對考生總體的作答速度和準確率分別進行估計。

在此基礎上,van der Linden(2007)提出2層模型。第一層模型選用三參數IRT模型(正態肩形模型Normal Ogive Model或logistic模型)對作答的對錯情況進行建模,同時選用對數正態模型對項目反應時間進行建模,公式如下:

f(uj,tj;ξj,ψ)=

(13)

其中,考生j的考生參數ξj有2個,分別為做題速度(τj)和能力值(θj);試題參數ψi有5個,分別為區分度(ai)、難度(bi)、猜測指數(ci)、時間消耗度(βi)、時間區分度(αi)。

第二層模型同樣包含2個模型,公式如下:

f(u,t;ξ,ψ)=

(14)

其中,考生參數ξj的取自于考生總體P,其參數符合多元正態分布,公式如下:

ξj～f(ξj;μP,ΣP)。

(15)

試題參數ψi同樣取值于多元正態分布:

ψi～f(ψi;μi,Σi)。

(16)

第二層模型在第一層模型的基礎上對考生總體的參數和題項間的關系進行了估計。層次模型框架(hierarchical framework)同樣采用了吉布斯采樣的方式進行參數估計。

自發布以來,層次框架模型廣受好評,多位研究者認為層次框架模型是一種插件模型(plugin model)(Bolsinova,Tijmstra,& Molenaar,2017;Molenaar,Bolsinova,& Vermunt,2018;Molenaar &de Boeck,2018),研究者可以將表示作答準確率的單維項目反應模型換成多維項目反應模型或認知診斷模型(Zhan,2022;Zhan,Man,Wind,& Malone,2022;詹沛達,2019),又或者多級計分模型(汪大勛,郭瑩瑩,2022),也可以將項目作答反應時間的對數正態模型換成多維反應時間模型(Zhan,Jiao,Man,Wang,& He,2021;Zhan,Jiao,Wang,& Man,2018;詹沛達,Jiao,Man,2022),還可以在模型中增加協變量(Qiao &Jiao,2022),郭小軍等(2022)還進一步探討了多維潛在特質速度之間可能存在層階關系,并提出了高階對數正態作答時間模型與雙因子對數正態作答時間模型。Ranger(2013)認為van der Linden的層次框架模型是標準化測驗中有關考生作答和考生作答反應的標準建模操作流程,Wang(2018)等研究者更是指出這種層次框架模型在考生作答和考生作答反應的多種統計建模中是最為流行的一種。嚴娟等(2022)將這種建模方法應用到了多維人格測驗中。

當然,我們也應注意到在層次框架模型以外,也有不少研究者嘗試提出其他類型的模型,其中比較重要的如雙向異常值檢測模型(two-way outliers detection model)(Chen,Lu,& Moustaki,2019)和線性模型(Molenaar &Bolsinova,2017;Molenaar,Tuerlinckx,& van der Maas,2015a,2015b),尤其線性模型是在層次框架模型基礎上發展而來。

3.1.3 與其他過程數據的聯合模型

隨著基于計算機的考試(CBT)進一步普及,考生越來越多的生物信息(如眼動、腦電、心率)開始被采集、記錄和分析,Man 和Harring(2021)在綜合對比多種生物信息和傳統考試信息的基礎上進行分析,提出了一種基于項目反應、作答反應時間、注視點個數的聯合建模,并用這種模型分析了團體作弊行為,他們通過對335名大學生的眼動實驗,驗證了模型具有較好的數據擬合性,也能量化呈現不同學生群體的作答準確率、作答效率和視覺參與度,為作弊甄別提供量化依據。在疫情的影響下,這一研究也為如何開展線上考試的作弊甄別提供了一種新的解決方案。還有研究者將作答反應時間數據、作答正誤數據以及作答中鼠標的拖拽和點擊等數據進行聯合建模(Liang,Tu,& Cai,2023),也為作弊甄別提供了一種新的研究方法。

3.1.4 個人擬合分析

本文前述模型需要通過個人擬合分析的方法判斷考生是否作弊。在考試甄別中,基于對數正態模型和層次框架模型的個人擬合方法分別為:以標準作答為基礎的索引法(Marianti,Fox,Avetisyan,Veldkamp,& Tijmstra,2014)和以層次框架模型為基礎的貝葉斯殘差分析法(van der Linden &Guo,2008)。

標準作答索引法(Marianti et al.,2014)是指在作答反應時間的對數正態模型的基礎上,基于Iz統計法(Drasgow,Levine,& Williams,1985)進行個人擬合分析,查看觀測到的考生項目作答反應時間數據在模型預估到的項目作答反應時間分布中的概率,并將該概率與門檻值C進行對比,判斷偏離情況,確定是否需要標注、告警。并基于公式1建立公式如下:

(17)

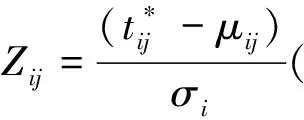
貝葉斯殘差分析法是在層次框架的基礎上提出2個公式,用以計算考生j在任意一個題項i作答中所用的項目反應時間的觀測值與預測值的差異,并計算在貝葉斯后驗分布中該觀測值出現的概率。如果考生在某個題項的作答反應時間過于短,則懷疑該考生有可能提前獲知題項,存在泄題(preknowledge)的問題;如果考生在某個題項的作答反應時間過于長,則懷疑該考生有可能是在背誦試題,用以對外售賣或者傳播。

概率計算公式采用了反常積分(Improper Integral)的計算方法,考生在某個題項答題時間短于預測值的概率的公式如下:

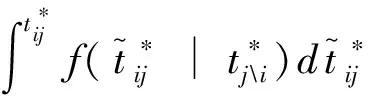
(18)

考生在某個題項答題時間長于預測值的概率的公式如下:

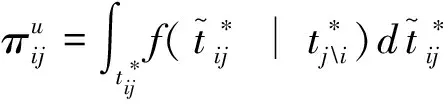
(19)

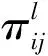
當然,也有研究者提出了其他的個人擬合分析方法,如在三參數的項目反應模型和項目作答反應時間的對數正態模型的基礎上提出混合模型法(mixed hierarchical model,MHM),構建異常作答指標Δij(第i個題項,第j個考生的異常作答情況),并對其進行建模運算(Wang et al.,2018),這種擬合方法層次框架模型的一種延伸和修正。

當數據污染情況較重時,殘差分析法對題目參數估計準確性會大幅降低,劉玥等(2022)利用混合模型法(MHM)對原有殘差計算方式進行優化,提出了固定參數標準化殘差法(conditional estimate standard residual,CSR),該方法先通過混合模型法(MHM)篩選正常作答的考生,進而獲得較為準確參數估計結果,研究顯示在數據污染較為嚴重時,該方法效果優于其他方法。

也有研究者在個人擬合統計量的基礎上嘗試使用變點分析法(change point analysis,CPA)進行異常作答甄別。張龍飛等(2020)對這種方法進行了系統介紹,變點分析的原理在于使用個人擬合分析統計量(person-fit statistics,PFS)判斷作答序列中是否存在可將該序列劃分為具有不同統計學屬性的兩個部分的點,常用的統計檢驗方法有基于似然比檢驗的Lmax法,基于Wald檢驗的Wmax法,基于得分檢驗的Smax法和基于加權殘差的Rmax法。鐘小緣等(2022)將變點分析拓展性的應用到了作答時間數據的分析中,發現此方法在加速作答檢測中效果較好,I型錯誤水平較低。

目前,有大量的研究者使用參數法進行建模和個人擬合,在檢出率和誤檢率方面都取得了不錯效果(Qian et al.,2016;Zopluoglu,Kasli,& Toton,2021)。但是,也有研究者對參數建模方法提出了批評(Man et al.,2018;Meijer &Sijtsma,2001),他們認為參數法存在著比較多的問題:一是算法過于復雜,如使用MCMC進行參數估計的時會因為迭代數、起始點、馬氏鏈長度等參數的設置造成不同;二是如果異常作答的數據較多,用單一模型進行數據擬合的難度將會變得非常大。

3.1.5 參數法在作弊甄別中的應用

參數法在近些年間獲得了廣泛應用,從本研究界定的“三類”作弊行為而言:這種作弊甄別方法在泄題和抄襲類的作弊行為的甄別中應用更多且更有效,但是在篡改答案型的作弊甄別中應用較少。這主要是因前兩類作弊行為會更加系統化、規模化的影響作答反應時間(Sinharay,2021)。從本文界定的“兩種”作弊行為而言:這種作弊甄別方法在團體作弊行為和個人作弊行為的甄別中都取得了不錯的效果,并且在團體作弊行為甄別中的效果更優。

在抄襲類作弊行為甄別中的應用。van der Linden基于作答反應時間開展二元對數正態模型(bivariate lognormal)建模,進行抄襲類作弊行為的甄別研究(van der Linden,2009)。二元對數正態模型主要是在對數正態模型的基礎上引入了2個考生在個別考試題項上作答反應的一致性參數ρjk,假定ρjk=0(即2個考生的作答沒有一致性)。但在觀測中,如果發現ρjk>0,并且大于門檻值C,則這2個考生之間可能存在著答案抄襲或者共謀作弊的情況。在實際的估算和檢驗中,van der Linden(2009)采用了LM檢驗的方法(Lagrange multiplier test,拉格朗日乘數檢驗)進行抄襲甄別確認。研究結果顯示,基于二元對數正態模型的抄襲甄別檢驗在實際數據中獲得了不錯的效果,尤其LM檢驗比普通的相關性檢驗能更好的反應2個考生之間的相似度。

在泄題類作弊行為甄別中的應用。考試泄題、考生提前獲取試題已經成為當前考試實踐中面臨的一個重要問題(Zopluoglu et al.,2021)。Eckerly(2017)對泄題類作弊甄別做了分類:一是針對泄題類作弊考生開展的甄別研究;二是針對泄題題項的甄別研究;三是同時針對作弊考生和泄題題項的甄別研究;四是針對團體作弊考生甄別研究。Eckerly(2017)指出,基于反應時間的泄題類作弊行為研究主要應用在第三類。前文介紹的2種參數建模方法在泄題類作弊甄別中均有應用:單純基于項目反應時間數據庫開展的泄題類作弊甄別研究有很多(Qian et al.,2016;Van der Linden &Van Krimpen-Stoop,2003;van der Linden &Guo,2008),基于項目反應時間數據和其他數據聯合建模進行作弊甄別的研究也有不少(Meijer &Sotaridona,2006;Wang et al.,2018;Zopluoglu,2019)。如,在一項基于真實數據的泄題甄別研究中(Qian et al.,2016),研究者從項目作答反應時間角度對兩個行業從業資格考試進行泄題甄別。該研究選定分屬于金融、衛健行業的2個行業準入考試,基于層次框架模型(hierarchical framework)(van der Linden &Guo,2008)進行作弊甄別。結果顯示,這種方法在檢出率和誤報率等指標中都獲得了比較好的結果,檢測出了111個題項中2個有可能被泄露的題項和1 172個考生中有2個有可能掌握泄題資料的考生。

在答案篡改類作弊行為甄別中的應用。目前尚未有研究者采用項目作答反應時間的方法針對考試篡改答案情況進行研究。這主要是因為考試篡改答案行為,如更改考生答案等,污染了原有的項目作答反應數據,不易識別。

在團體類作弊行為甄別中的應用。根據本文的分類,團體類型的作弊也會出現如答案抄襲和共謀作弊(answer copying and collusion)、泄題(preknowledge)、考試篡改答案(test tampering)等類型。有研究者提出了一種多維數據聯合建模的方式開展團體作弊行為中的泄題行為甄別,并取得了較好的作弊甄別效果(Man &Harring,2021)。也有研究者更新了對數正態模型(Cengiz Zopluoglu et al.,2021),采用了增加門控制機制(Gating Mechanism)對數正態模型的方法對團體泄題類型的作弊進行了甄別研究。該結果雖然顯示甄別效果較好,但是研究者也坦陳了效應量的問題。因為不同數據集的效應量可能來自于多種因素,如考生特點、泄題的具體情況、和試題的特點等,這種研究方法不具有普適性,研究者需要針對數據特點選擇建模方法和擬合分析方法。

3.2 非參數建模法及應用

非參數建模法則主要采用K-L散度(相對熵)的方法進行建模,當然,研究者也會在建模中引入其他作答數據,如作答準確率、考生的其他生物信息等。非參數法與參數法的本質不同在于,非參數法把考生的作答時間看成了一種離散變量,而參數法則把考生的作答時間看作了一種連續變量,且其對數服從正態分布。非參數的這種檢測方法在模擬數據和真實數據中都取得了較好的效果(Man,Harring,Ouyang,& Thomas,2018),尤其是在同樣的數據分析中,取得了比標準作答索引法(Marianti et al.,2014)相對更優的效果。Man等研究者(2018)針對參數建模的缺點,采用K-L散度(Kullback-Leibler Divergence,也稱相對熵)進行了基于項目作答反應時間的作弊甄別研究。K-L散度可以度量兩種分布之間的差異。在研究中,研究者使用相對熵的方法對考生個人的作答反應時間分布情況和考生總體的作答反應時間分布情況進行了對比,公式如下:

(20)

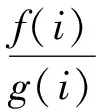
有研究者在非參數建模中引入了作答準確率的數據,對項目作答反應時間進行了細分,提出了“有效反應時間”(effective response time)的概念,用以描述個體考生答對某一題項所花費的時間(Meijer &Sotaridona,2006)。研究者假定,獲得泄題(preknowledge)數據的考生作答時間與普通考生有較大差異,并采用堪薩斯大學528位大學一年級學生參與的摘要推理考試(abstract reasoning test,ART)數據進行假設檢驗。研究發現,基于“有效反應時間”模型的誤檢率(type I error)較低。隨后,他們又在真實數據的基礎上生成了模擬數據,在真實考試數據中抽樣選取部分考生,然后將其在原始考試題項中比例為50%或者75%的題項上的作答反應時間改為原始數據的1/2或者1/4,發現檢出率較以往的方法有了大幅提升。但是也應該注意到,這項研究中的模擬數據情況較為極端(Meijer &Sotaridona,2006)。

4 總結與討論

4.1 項目作答反應時間數據不能被污染

有關項目作答反應時間的考試作弊甄別研究成立的一個基本假設為:考生沒有刻意操縱自己的作答時間。但是,如果作弊考生了解到,現有作弊甄別技術是通過監控其作答時間進行作弊甄別的,考生有可能會刻意控制自己的項目作答時間,這將為甄別效果帶來巨大的挑戰。不過,也應該看到,考生在刻意控制作答時間的時候,眼動等其他生物信息、敲擊鍵盤的信息等會與積極作答的考生有所不同(Nagy &Ulitzsch,2021;Zopluoglu,2019),所以將考生作答反應時間與其他考生信息進行聯合建模將有力的促進研究者優化建模方法、提升模型擬合度、提高作弊的甄別效率。

另外,還需要注意到,也有研究者(郭小軍,羅照盛,2019;Domingue et al.,2022)對速度與準確率之間的權衡進行了分析與討論,他們認為作答反應時間與作答準確性之間可能不是線性關系,隨著反應時間的增加,準確率提高到某種程度之后會停滯或者降低。這些研究對有關項目作答反應時間數據的假設也提出了一定挑戰。

4.2 多類型過程數據聯合建模成為趨勢

隨著基于計算機的考試(Computer Based Tests)進一步普及,隨著各類信息追蹤設備和軟件的輕量化、普及化發展,考生在考試中的各類信息可以被實時搜集(Man &Harring,2021),這些信息既包含機械信息:如作答反應時間、如擊鍵記錄(keystroke logging);也包含生物信息如眼動追蹤、注視點個數、眨眼頻率(blinking rates)、瞳孔直徑(pupil diameters)、血氧度(blood oxygen level)等(Liang et al.,2023;Man,Harring,& Zhan,2022)。這些信息可以和項目作答反應時間、考試作答數據等其他數據進行聯合建模,進而量化考生的總體情況,從更全面的角度、更為精確得開展作弊甄別。

在這種多類型數據的聯合應用過程中,不僅要擴大數據量、拓展數據種類,也要進一步提升數據模型的擬合優度。有研究者嘗試將機器學習、深度學習的研究方法應用到了作弊甄別中,取得了不錯的效果。在機器學習方面,Man等(2019)研究者對多種機器學習方法進行了對比,包括無監督學習方法K均值算法(K-means),有監督學習方法支持向量機(SVM)、K近鄰(K-Nearest Neighbor)、隨機森林(Random Forests)等,建議在作弊甄別實踐中將多種機器學習方法合并使用,可以獲得較好的檢測效果。Pan 等采用機器學習方法進行了泄題題項和獲取泄題信息的考生的作弊甄別(Pan &Wollack,2021,2023)。也有研究者采用機器學習中集成學習的方法開展作弊甄別,Zhou和Jiao(2022)使用集成學習的stacking算法開展了大規模考試的作弊甄別,Zopluoglu(2019)采用了集成學習中的boosting的方法進行了作弊甄別,兩個模型越都取得了較好的作弊甄別效果。Meng和Ma(2023)也選定了11種特征,并使用隨機森林(Random Forests)、邏輯回歸(Logistic Regression)、支持向量機(SVM)等方法訓練模型,發現支持向量機(SVM)和隨機森林(Random Forests)在作弊甄別中的效果更好。在深度學習方面,Kamalov等研究者采用循環神經網絡的方法(RNN)進行了作弊甄別(Kamalov,Sulieman,& Santandreu Calonge,2021)。Zhen和Zhu(2023)采用了深層神經網絡TabNet進行了作弊甄別,研究發現相較于其他機器學習模型而言,TabNet具有較強的優勢效果。

同時,如基于卷積神經網絡(CNN)和YOLO算法的機器視覺研究也開始逐漸被使用到考場監控視頻的識別研究中(竇剛,劉榮華,范誠,2021),研究者也可以嘗試將考場抓取的機器視覺信息與作答反應模型、項目作答反應時間模型等數據聯合使用,提升作弊甄別的效率。

4.3 模型應用范圍仍需進一步拓展

從研究數據角度看,大部分研究者都拿不到真實數據,或同一數據集被反復使用(Zopluoglu et al.,2021),模擬數據研究的支撐作用較大(van der Linden &Guo,2008),采樣軟件有JAGS或R語言的LNIRT等。換言之,雖然科研領域對這類作弊甄別模型研究較多,但是在實際考試中的模型的應用仍然較少。隨著國內基于計算機的考試(Computer Based Tests)大規模普及,考試組織方和考試研究單位可以積極開展聯合協作,推動作答反應時間類數據的采集和作答反應時間類作弊甄別模型的廣泛應用,提升考試的安全性。