機電復(fù)合傳動高線速轉(zhuǎn)子-行星齒輪系統(tǒng)耦合振動特性

曾根，馬長軍，龐大千，李同輝，張楠

(1.北京理工大學(xué) 機械與車輛學(xué)院，北京 100081;2.中國北方車輛研究所，北京 100072;3.車輛傳動重點實驗室，北京 100072)

0 引言

行星齒輪系統(tǒng)由于結(jié)構(gòu)簡單、傳遞功率大及技術(shù)成熟等特點，廣泛運用于各類電驅(qū)動系統(tǒng)中。目前對于行星齒輪系統(tǒng)的研究大多集中于行星齒輪排本身故障診斷及動態(tài)特性研究方面［1-2］，而對于齒輪系統(tǒng)于高線速度轉(zhuǎn)子耦合振動特性的研究卻非常匱乏。電驅(qū)動系統(tǒng)由于驅(qū)動電機的存在，與傳統(tǒng)內(nèi)燃機功率輸出方式截然不同，這就造成了傳統(tǒng)行星齒輪動力學(xué)研究已經(jīng)很難適用于新型的電驅(qū)動系統(tǒng)中，在機電復(fù)合傳動系統(tǒng)驅(qū)動電機的高速作用下，與電機主軸直連的行星齒輪系統(tǒng)振動特性將與電機整個轉(zhuǎn)子產(chǎn)生耦合作用，當(dāng)振動幅值到達(dá)一定階段后，有可能出現(xiàn)轉(zhuǎn)子掃膛或齒輪失效等情況發(fā)生。

在行星齒輪系統(tǒng)研究方面，F(xiàn)ernandez 等［3］和Chang 等［4］先后提出利用有限元法和接觸力學(xué)法相結(jié)合的混合模型，用該模型計算了外嚙合剛度和齒輪傳遞誤差。Ambarisha 等［5］研究了行星齒輪的復(fù)雜非線性動力學(xué)，分析了嚙合剛度和齒面接觸對系統(tǒng)固有特性的影響。Liu 等［6］研究了兩級行星齒輪系統(tǒng)的非線性動力學(xué)，推導(dǎo)出考慮滑動摩擦及齒側(cè)間隙的時變嚙合剛度計算公式，用以分析系統(tǒng)的動態(tài)響應(yīng)。Zhang 等［7］研究了不同構(gòu)件浮動對載荷分配和周期運動的影響，用于改善復(fù)合行星齒輪系統(tǒng)的載荷分配為和抗混沌運動。Cui 等［8］在彎扭耦合模型中，提取了系統(tǒng)的固有頻率和模態(tài)振型，從而分析了系統(tǒng)的動態(tài)性能。Meng 等［9］為了更加準(zhǔn)確地揭示行星輪系在健康狀況下和故障狀況下的振動信號特征，對系統(tǒng)進(jìn)行了振動特性分析。Kahraman 等［10］建立了單級行星齒輪傳動系統(tǒng)純扭轉(zhuǎn)動力學(xué)模型，該模型針對振動產(chǎn)生的主導(dǎo)因素扭轉(zhuǎn)振動，分析了該動力學(xué)模型的固有特性，可用于對行星齒輪系統(tǒng)固有頻率的分析［11］、動力學(xué)響應(yīng)求解［12］以及系統(tǒng)運動狀態(tài)的定性分析［13］。

在機電復(fù)合傳動系統(tǒng)方面，胡紀(jì)濱等［14］對機電復(fù)合傳動系統(tǒng)的扭振進(jìn)行了研究。張偉等［15］對機電復(fù)合傳動系統(tǒng)固有振動特性進(jìn)行了分析。周傳月等［16］分析了柴油發(fā)電機組軸系的扭轉(zhuǎn)振動特性，揭示了軸系臨界轉(zhuǎn)速、振型等。Zapomel 等［17］研究了轉(zhuǎn)子裝配和制造誤差對旋轉(zhuǎn)機械系統(tǒng)橫向振動的影響，且通過改變旋轉(zhuǎn)支撐軸剛度可改善其橫向振動的效果。Werner［18-19］用轉(zhuǎn)子動力學(xué)模型分析了電機轉(zhuǎn)子在動偏心情況下啟動過程的橫向振動，李志農(nóng)等［20］利用分?jǐn)?shù)階微積分對含有裂紋的轉(zhuǎn)子系統(tǒng)非線性動力學(xué)特性進(jìn)行了研究。

然而，以往的研究雖然已經(jīng)對行星齒輪系統(tǒng)及機電復(fù)合傳動系統(tǒng)進(jìn)行了較為深入的研究，但都是在低線速度的條件下進(jìn)行，轉(zhuǎn)子與行星齒輪系統(tǒng)的耦合振動特性并無不明顯體現(xiàn)。因此，本文建立了機電復(fù)合傳動系統(tǒng)高線速轉(zhuǎn)子-行星齒輪系統(tǒng)耦合振動仿真模型，通過對不同轉(zhuǎn)速下轉(zhuǎn)子-行星齒輪系統(tǒng)振動特性以及模態(tài)振型進(jìn)行分析研究，揭示出不同轉(zhuǎn)速下機電復(fù)合傳動轉(zhuǎn)子-行星齒輪系統(tǒng)振動規(guī)律，為機電復(fù)合傳動系統(tǒng)高速化發(fā)展提供有力支撐。

1 轉(zhuǎn)子-行星齒輪系統(tǒng)動力學(xué)模型

齒輪傳動具有承載能力大、傳動精度高、傳動功率恒定等特點，被廣泛地應(yīng)用于機械行業(yè)中的各個領(lǐng)域，其性能和質(zhì)量直接影響到整機產(chǎn)品的技術(shù)指標(biāo)，準(zhǔn)確地描述轉(zhuǎn)子-行星齒輪系統(tǒng)的動態(tài)特性對傳動系統(tǒng)的設(shè)計就具有重要意義［21-22］，由于轉(zhuǎn)子振動的影響，行星齒輪系統(tǒng)與轉(zhuǎn)子的耦合系統(tǒng)會產(chǎn)生中心偏移現(xiàn)象，這也是轉(zhuǎn)子-行星齒輪系統(tǒng)耦合振動的理論基礎(chǔ)，齒輪-轉(zhuǎn)子系統(tǒng)動力學(xué)模型如圖1所示。

圖1 齒輪轉(zhuǎn)子系統(tǒng)動力學(xué)模型Fig.1 Dynamic model of the gear-rotor system

圖1 中的JM、JL、J1和J2分別是主動輪、負(fù)載輪以及主從動齒輪的轉(zhuǎn)動慣量，θ、θL、θ1和θ2分別是主動輪、負(fù)載輪以及主從動齒輪的旋轉(zhuǎn)角度，k1和k2分別是主/從動轉(zhuǎn)子的扭轉(zhuǎn)剛度系數(shù)，c1、c2分別是驅(qū)動/從動轉(zhuǎn)子的扭轉(zhuǎn)阻尼系數(shù)。如圖1(b) 所示的動力學(xué)模型，kv和cv分別是主/從動齒輪之間嚙合的剛度系數(shù)和阻尼系數(shù)，e 為齒輪傳遞誤差。根據(jù)主動輪的特性，在計算主動輪的速度波動時，θ、θL、θ1和θ2為廣義坐標(biāo)，使用Newton-Euler 拉方法，建立動力學(xué)公式為

式中:rb1、rb2為兩個基圓的半徑;齒輪的動態(tài)嚙合力F 為

當(dāng)主動輪以恒定速度旋轉(zhuǎn)時，角度θ 不再用作廣義坐標(biāo)，而是用作已知量:

式中:x 為兩個齒輪在嚙合線上的相對位移;φ1、φ2分別為主、從動轉(zhuǎn)子的扭轉(zhuǎn)角。

式(3) 代入式(1)，可得

將式(2) 代入式(4)，可以得到以下矩陣方程:

式中:M 為系統(tǒng)質(zhì)量矩陣;q 為廣義坐標(biāo)矩陣。

C 和K 為系統(tǒng)剛度矩陣以及系統(tǒng)阻尼矩陣，D為系統(tǒng)廣義力矩陣。

根據(jù)定軸齒輪動力學(xué)方程可以推導(dǎo)出行星齒輪系統(tǒng)動力學(xué)方程，太陽輪、齒圈、行星輪以及行星架的運動微分方程如式(11)～式(14) 所示，動力學(xué)關(guān)系如圖2 所示。在圖2 中，設(shè)置有3 種類型坐標(biāo)系用于描述行星齒輪系統(tǒng): 大地坐標(biāo)系OXY，固定在行星架上并隨其轉(zhuǎn)動的動坐標(biāo)系oxy，固定在行星輪上的動坐標(biāo)系opnxpnypn，n=1，2，…，N，N 為行星輪個數(shù)，其中opnxpnypn坐標(biāo)軸軸線與oxy 坐標(biāo)軸軸線相平行。每個元件有x、y、θ 三個方向自由度，θc為行星架在大地坐標(biāo)系OXY 中的轉(zhuǎn)角，θs及θr分別為太陽輪、內(nèi)齒圈在動坐標(biāo)系oxy 中的轉(zhuǎn)角，θpn為行星輪在動坐標(biāo)系opnxpnypn中的轉(zhuǎn)角。Ts為作用在太陽輪的驅(qū)動力矩，Tc為作用在行星架上的負(fù)載力矩。φn為第n 個行星輪在oxy 中的位置角，φn=2π(n -1)/N，δpnx、δpny、δpnt分別為行星輪與行星架在x 軸、y 軸及切向方向的相對位移，可由坐標(biāo)系oxy 與坐標(biāo)系opnxpnypn的位置關(guān)系計算得出，F(xiàn)spn和Frpn為動態(tài)嚙合力，kc、cc分別為行星架的剛度系數(shù)和阻尼系數(shù)，kr和cr分別為外齒圈的剛度系數(shù)和阻尼系數(shù)，ks和cs分別為太陽輪的剛度系數(shù)和阻尼系數(shù)，kp和cp分別為行星輪的剛度系數(shù)和阻尼系數(shù)，kpnx和cpnx分別為行星輪在動坐標(biāo)下的剛度系數(shù)及阻尼系數(shù)，kspn、cspn和espn分別為太陽與行星輪嚙合時剛度系數(shù)、阻尼系數(shù)和傳遞誤差，krpn、crpn和erpn分別為齒圈與行星輪嚙合時剛度系數(shù)、阻尼系數(shù)和傳遞誤差，krt和crt分別為齒圈切向方向的剛度系數(shù)和阻尼系數(shù)。

圖2 行星齒輪系統(tǒng)動力學(xué)關(guān)系示意圖Fig.2 Schematic diagram of dynamic relationship of the planetary gear system

2 轉(zhuǎn)子-行星齒輪系統(tǒng)建模及求解過程

由于ADAMS 軟件提供的實體建模功能并不適合于復(fù)雜的3D 曲面建模，所以本文利用CREO 軟件對齒輪實體進(jìn)行模型，而后由標(biāo)準(zhǔn)化數(shù)據(jù)接口導(dǎo)入ADAMS 軟件中進(jìn)行仿真分析。

2.1 接觸力的定義及選擇

在ADAMS 軟件中對齒輪進(jìn)行約束和設(shè)置接觸時，齒輪間接觸力參數(shù)的設(shè)置尤為關(guān)鍵，正確計算齒輪件接觸力才可能得到與事實相符的仿真結(jié)果。本文選用IMPACT 函數(shù)來計算接觸力。

IMPACT 函數(shù)表達(dá)式為

根據(jù)赫茲彈性接觸理論可知

式中: a 為接觸半寬;E*為兩接觸物體彈性模量與泊松比的比值為兩接觸物體的彈性模量，μ1、μ2為兩接觸物體的泊松比。

由此可得到撞擊時接觸法向力P 和變形δ 的關(guān)系為

式中:K 為接觸剛度，取決于碰撞物體的材料及結(jié)構(gòu)形狀，

2.2 轉(zhuǎn)子-行星齒輪系統(tǒng)建模與參數(shù)設(shè)計

轉(zhuǎn)子-行星齒輪系統(tǒng)簡圖如圖3 所示，轉(zhuǎn)子直徑為320 mm，總長410 mm，圖4 為轉(zhuǎn)子-行星齒輪系統(tǒng)三維模型示意圖，表1 為系統(tǒng)參數(shù)。

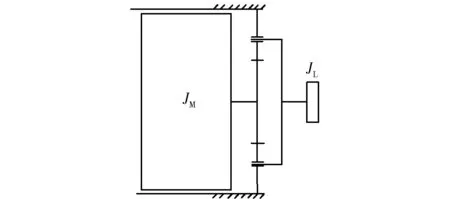
圖3 轉(zhuǎn)子-行星齒輪系統(tǒng)簡圖Fig.3 Diagram of the rotor-planetary gear system

圖4 轉(zhuǎn)子-行星齒輪系統(tǒng)三維模型示意圖Fig.4 Three dimensional model of the rotor-planetary gear system

表1 轉(zhuǎn)子-齒輪系統(tǒng)參數(shù)Table 1 Rotor-gear system parameters

3 算例及結(jié)果分析

將對轉(zhuǎn)子-行星齒輪系統(tǒng)進(jìn)行仿真分析，通過分析不同轉(zhuǎn)速下系統(tǒng)的頻域變化，揭示其耦合振動規(guī)律。為了獲得更精確的頻域響應(yīng)，屏蔽了軸承在正常工作條件下的振動，以減少對系統(tǒng)的振動干擾。為了模擬實際工況，系統(tǒng)轉(zhuǎn)子加載轉(zhuǎn)速為3 000～12 000 r/m，行星架加載扭矩為300 N·m，轉(zhuǎn)子線速度加載為50.24～200.96 m/s，從式(14) 可以得出系統(tǒng)的剛度為6.32 ×105，力指數(shù)eF為1.5，阻尼為46，穿透深度為0.01 mm，轉(zhuǎn)子-行星齒輪系統(tǒng)ADAMS模型如圖5 所示。

圖5 轉(zhuǎn)子-行星齒輪系統(tǒng)仿真模型Fig.5 Simulation model of the rotor-planetary gear system

3.1 不同轉(zhuǎn)速下轉(zhuǎn)子-行星齒輪系統(tǒng)振動分析

對3 000～12 000 r/m 轉(zhuǎn)速區(qū)間的振動數(shù)據(jù)進(jìn)行短時傅里葉變換(STFT)，4 000 r/m 下轉(zhuǎn)子-行星齒輪系統(tǒng)的齒輪嚙合主頻STFT 譜如以及軸頻如圖6 所示。

圖6 4 000 r/m 下轉(zhuǎn)子-行星齒輪系統(tǒng)太陽輪振動STFT 譜Fig.6 STFT spectrum of sun gear vibration of the rotor-planetary gear system at 4 000 r/m

由圖6 可以看到在3 000～6 000 r/m 轉(zhuǎn)速區(qū)間內(nèi)，太陽輪振動幅值雖然在逐漸上升，但上升速率較為緩慢，當(dāng)轉(zhuǎn)速超過6 000 r/m 后，太陽輪振動幅值隨著轉(zhuǎn)速的增加而逐漸升高，并且升高速率也逐漸大，如圖7 所示。

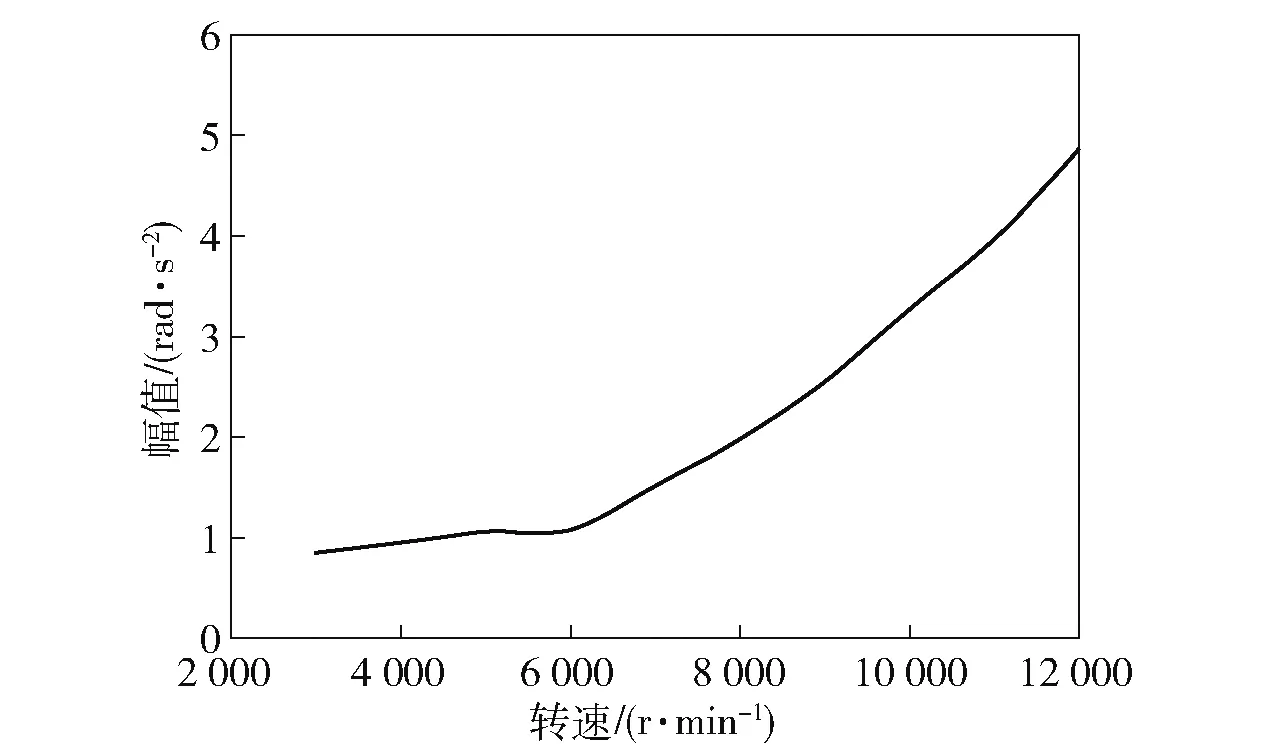
圖7 3 000～12 000 r/m 轉(zhuǎn)速期間內(nèi)太陽輪振動STFT 幅值Fig.7 STFT amplitude of sun gear vibration in the speed range of 3 000～12 000 r/m

由圖7 可以看到在3 000～12 000 r/m 轉(zhuǎn)速區(qū)間內(nèi)，傳動軸的振動幅值始終保持一定速率增大，與太陽輪不同的是傳動軸在3 000～6 000 r/m 轉(zhuǎn)速區(qū)間內(nèi)并沒有出現(xiàn)幅值上升緩慢的現(xiàn)象，而且隨著轉(zhuǎn)速的增加保持上升速度持續(xù)增大，如圖8 所示。

圖8 3 000～12 000 r/m 轉(zhuǎn)速期間內(nèi)傳動軸振動STFT 幅值Fig.8 STFT amplitude of internal transmission shaft vibration at 3 000～12 000 r/m

圖9 和圖10 為3 000 r/m 與4 000 r/m 下太陽輪與行星輪嚙合瞬態(tài)接觸力，可以看到在4 000 r/m轉(zhuǎn)速下，瞬態(tài)接觸力上限幅值明顯增大，并且整體浮動區(qū)間在3 000 N 以上。在3 000 r/m 轉(zhuǎn)速下，瞬態(tài)接觸力上限幅值較4 000 r/m 轉(zhuǎn)而言有所減小，并且整體浮動區(qū)間在3 000 N 一下。

圖9 4 000 r/m 下太陽輪與行星輪瞬態(tài)接觸力Fig.9 Transient contact force between the sun gear and the planetary gear at 4 000 r/m

圖10 3 000 r/m 下太陽輪與行星輪瞬態(tài)接觸力Fig.10 Transient contact force between the sun gear and the planetary gear at 3 000 r/m

3.2 實驗驗證

為了驗證計算機仿真的可靠性，將文獻(xiàn)［23］中的實驗數(shù)據(jù)作為參考標(biāo)準(zhǔn)，實驗［23］中對從動輪人為施加裂紋故障，裂紋深度為1 mm、2 mm、3 mm、4 mm，主動輪加載1 000 r/m 轉(zhuǎn)速，圖11 為實驗現(xiàn)場照片。

圖11 齒輪系統(tǒng)實驗臺示意圖Fig.11 Schematic diagram of the gear system test bench

對文獻(xiàn)［23］中實驗的模型進(jìn)行3D 建模并導(dǎo)入ADAMS 軟件中進(jìn)行計算機仿真實驗。本文選取文獻(xiàn)［23］中從動輪3 mm 裂紋處理實驗條件進(jìn)行仿真實驗對比，分別對無故障齒輪-轉(zhuǎn)子系統(tǒng)以及3 mm 裂紋處理齒輪-轉(zhuǎn)子系統(tǒng)進(jìn)行仿真，仿真結(jié)果快速傅里葉變換(FFT) 如圖12 所示。

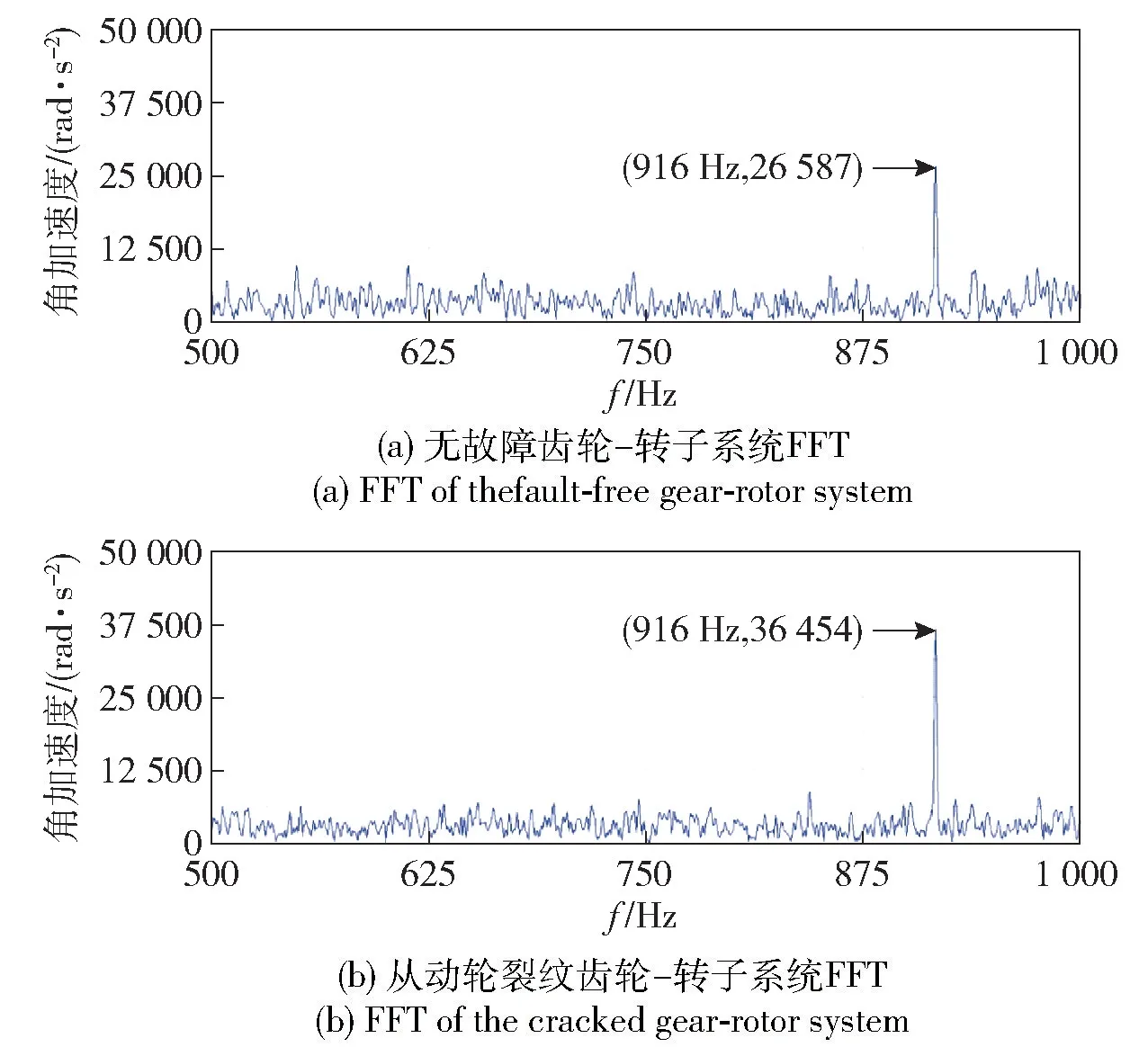
圖12 無故障與裂紋處理后的齒輪-轉(zhuǎn)子系統(tǒng)FFTFig.12 FFT of the gear-rotor system after fault free and crack treatments

通過對實際實驗?zāi)Ｐ瓦M(jìn)行計算機仿真可以看出，在實際實驗所得數(shù)據(jù)與計算機仿真所得真實數(shù)據(jù)總體趨勢基本相符，數(shù)據(jù)對比如表2 所示。

表2 不同故障狀態(tài)下實驗與仿真結(jié)果Table 2 Comparison between experiment at and simulatied results under the differen failur conditions

4 模態(tài)分析

建立轉(zhuǎn)子-齒輪系統(tǒng)模態(tài)有限元分析模型如圖13 所示，根據(jù)轉(zhuǎn)子-齒輪系統(tǒng)實際支撐情況在分析軟件內(nèi)對其進(jìn)行約束施加，保證行星齒輪外齒圈固定，有限元網(wǎng)格劃分為1 008 743 網(wǎng)格數(shù)，1 525 973節(jié)點數(shù)，保證了網(wǎng)格的密度。

圖13 轉(zhuǎn)子齒輪系統(tǒng)模態(tài)有限元仿真分析模型Fig.13 Modal finite element analysis model of the rotor-gear system

對轉(zhuǎn)子-齒輪系統(tǒng)前30 階模態(tài)進(jìn)行了計算，結(jié)果如表3 所示，可以看到前6 階頻率均比較小，當(dāng)超過6 階后系統(tǒng)固有頻率明顯增大，而后隨著階次的增加，頻率逐漸增大，前30 階模態(tài)結(jié)果如圖14 所示，可以清晰地看到前30 階模態(tài)的變化趨勢。為了研究前9 階模態(tài)的變化情況，提取了前9 階模態(tài)振型三維圖，如圖15 所示，可以看到前3 階振型均以轉(zhuǎn)子振動為主，到4 階以后開始有齒輪和軸參與，到7 階就開始只有行星齒輪系統(tǒng)和軸參數(shù)振動，根據(jù)圖12 可以發(fā)現(xiàn)，前30 階固有頻率有3 個瞬時增大點，分別為7 階模態(tài)、17 階模態(tài)以及27 階模態(tài)，在后續(xù)的優(yōu)化設(shè)計過程中可以著重關(guān)注這3 個點的振動狀況，從而有效規(guī)避系統(tǒng)工作在共振區(qū)間內(nèi)。

表3 高線速轉(zhuǎn)子-行星齒輪系統(tǒng)前30 階模態(tài)分析結(jié)果Table 3 First 30-order modal analysis results of the high linear speed rotor-planetary gear system

圖14 高線速轉(zhuǎn)子-行星齒輪系統(tǒng)前30 階模態(tài)結(jié)果曲線圖Fig.14 Curve of the first 30-order modal results of the high linear speed rotor-planetary gear system

圖15 高線速轉(zhuǎn)子-行星齒輪系統(tǒng)前9 階模態(tài)振型Fig.15 First 9-order modal shapes of the high linear speed rotor-planetary gear system

5 結(jié)論

1) 本文建立了機電復(fù)合傳動系統(tǒng)高線速轉(zhuǎn)子-行星齒輪動力學(xué)仿真模型，對不同轉(zhuǎn)速下的高線速轉(zhuǎn)子-行星齒輪系統(tǒng)模型進(jìn)行了仿真分析。

2) 高線速轉(zhuǎn)子-行星齒輪系統(tǒng)在3 000～6 000 r/m轉(zhuǎn)速區(qū)間內(nèi)，太陽輪振動幅值上升緩慢，當(dāng)轉(zhuǎn)速達(dá)到6 000 r/m 后，太陽輪振動幅值升高速逐漸大。

3) 不同轉(zhuǎn)速下太陽輪與行星輪嚙合瞬態(tài)接觸力特性有所不同，在4 000 r/m 轉(zhuǎn)速時，瞬態(tài)接觸力在3 000 N 以上波動幅值明顯增大，在3 000 r/m轉(zhuǎn)速時，瞬態(tài)接觸力在3 000 N 以下波動幅值明顯增大，并且整體浮動區(qū)間在3 000 N 以下。

4) 高線速轉(zhuǎn)子-齒輪系統(tǒng)的前6 階固有頻率較小，7 階后的系統(tǒng)固有頻率明顯增大。3 階模態(tài)振型均以轉(zhuǎn)子振動為主，4 階模態(tài)以后開始有齒輪和軸參與振動，到7 階模態(tài)就開始只有行星齒輪系統(tǒng)和軸參數(shù)振動，前30 階固有頻率有3 個瞬時增大點，分別為7 階模態(tài)、17 階模態(tài)以及27 階模態(tài)。