中美股市跳躍溢出效應及跳躍對未來波動的影響研究

潘群星，孫羽佳，高天晴，杜修立

（南京財經大學金融學院，江蘇南京 210023）

一、引言

在“美國優先”政策的驅動下，美國經濟形勢曾一度向好，這種向好態勢在股票市場上也有所體現。截至2020年2月14日，標普500指數的市盈率已經達到24.74倍，平均市凈率超過3.65倍，創近十年以來新高。然而，突如其來的新冠疫情造成美國三大股指在2020年3月9日至18日間發生了4次一級熔斷，美股市場成為疫情沖擊的“重災區”。同樣受疫情的影響，上證綜指在2020年3月份下跌了4.5%，第一季度累計下跌9.8%；滬深300指數在同年3月份下跌了6.4%，第一季度累計下跌10%；這些指數均創2019年5月以來最差月度表現和2018年第四季度以來最差季度表現。美國股市作為全球最大的股票市場，其動蕩必然會對全球股票市場造成沖擊；而作為全球第二大股票市場、第一大新興市場的中國股市在反映美國股市等外圍市場信息的同時，也具備了影響外圍市場的能力（李紅權等，2011）[1]。

股市作為經濟發展的晴雨表，在疫情沖擊下更能及時反映人們的行為和對未來經濟的預期。疫情暴發初期，紛繁復雜的信息和嚴峻的形勢造成投資者的恐慌情緒持續蔓延。據芝加哥期權交易所公布的信息，“恐慌指數”（VIX）①VIX指數是芝加哥期權交易所于1993年推出，它是以標普500指數期權的隱含波動率加權平均編制的。在2020年3月18日一度狂飆至85.47，為2008年金融危機以來最高位。不斷擴散的恐慌情緒與經濟活動的停滯可能會引起股市的大幅波動，而該波動又可分解為連續成分和跳躍成分。資產價格在短時間內出現非連續的大幅波動的現象被稱為跳躍（Glosten和Milgrom，1985；西村友作和門明，2012；向健凱等，2017）[2-4]，它包含上跳和下跳，這些跳躍由一個市場傳遞到另一個市場的過程就是跳躍溢出。

跳躍效應與傳染效應是伴隨金融市場的兩種常規現象，特別是在危機暴發時期，一個國家金融市場的跳躍在傳染的推動下將引起本國與他國相關市場跳躍（周偉和何建敏，2012）[5]。探討疫情背景下中美股市的跳躍溢出以及跳躍對未來波動的影響，具有一定的意義。

第一，全球前兩大經濟體的股票市場在疫情期間都受到了極大的沖擊，通過研究其跳躍溢出，可以發現最大的發達市場與最大的新興市場在面臨極端風險時是如何相互影響、相互作用的。

第二，研究疫情暴發前后中美股市跳躍溢出對投資者如何規避突發公共衛生事件造成的極端風險具有一定的指導價值。

第三，跳躍對未來波動率影響的預測有利于投資者做出正確的預判，對資產進行有效配置，以減少極端風險帶來的損失。

二、文獻回顧

國外學者對于跳躍的度量可以追溯到1967年，Press（1967）[6]提出了復合事件模型，他通過引入泊松過程來度量市場跳躍現象。Akgiray和Booth（1988）[7]對其展開了進一步研究，構建了混合GARCH跳躍模型。但上述模型都假定跳躍參數服從常系數泊松過程，并且認為跳躍強度和次數是跨期獨立的，即一個時期的跳躍現象與前后不同時期價格的跳躍沒有關系。隨后，Kou（2002）[8]提出了一種價格及其波動率均存在跳躍現象的雙指數跳躍擴散模型，借此來刻畫金融市場的價格波動。任楓等（2009）[9]在此基礎上構建了一種非對稱雙指數跳躍擴散模型，并提出基于馬爾科夫鏈蒙特卡洛（MCMC）算法的模型求解，結果表明非對稱雙指數跳躍擴散模型能夠更好地體現資產價格分布的尖峰厚尾以及有偏性特征。Duffie等（2000）[10]提出了收益與波動都存在跳躍的兩種雙指數跳躍擴散模型：跳躍獨立隨機波動率（SVIJ）模型和SVCJ模型。Eraker等（2003）[11]比較了隨機波動率（SV）、隨機波動跳躍（SVJ）、SVIJ和SVCJ等四種模型，發現SVCJ模型對金融資產的跳躍溢出有著最佳的擬合度。

關于跳躍溢出效應，國內也有一些學者利用SVCJ模型展開過探索。劉慶富和許友傳（2011）[12]在研究國內外非同步期貨交易市場之間的跳躍溢出時發現國內外期貨市場存在顯著的跳躍溢出效應，并且國內的跳躍溢出頻度更高。宮曉莉等（2018）[13]通過構建廣義雙指數分布的跳躍擴散（GDED-SVCJ）模型研究了中國股指期現貨市場的波動和跳躍特征，發現期貨收益和現貨收益上漲與下跌概率不對稱，現貨波動強度低于期貨波動。王蘇生等（2019）[14]運用SVCJ模型、傅里葉變換以及MCMC等方法分析了上證50ETF期權市場波動率的風險溢價，研究表明波動率溢價具有時變特征，在市場急劇動蕩時期，投資者購買期權對沖波動風險的意愿較高。另外，A?t-Sahalia等（2015）[15]提出用Hawkes過程來捕獲時間和跨資產的跳躍集群或金融傳染，發現美國的跳躍往往在大多數其他市場得到迅速反應，而反向傳播則不明顯。由于該方法可以提供Hawkes過程的反饋方面，還可以提供跳躍導致更多的跳躍這一直觀的因果解釋，隨后出現了一系列采用Hawkes過程來研究跳躍傳染的文獻，如陳淼鑫和徐亮（2019）[16]以及李福興等（2020）[17]的研究。王茹婷等（2019）[18]則是選擇日內跳躍Logistic模型對降噪后高頻數據的日內跳躍情況進行檢測。綜上所述，關于收益率跳躍的研究是金融領域的一個熱點問題。

為了模擬跳躍對未來波動的影響，Creal等（2013）[19]提出了一種基于得分函數的時變參數建模框架——GAS模型。該模型是一種觀測值驅動模型，能夠充分利用分布信息，且隨機參數完全由過去的信息所預測。在GAS模型的框架下，不同的分布對應不同的得分函數形式以及形狀特征。Bernardi和Catania（2016）[20]比較了基于不同分布的GAS模型以及其他模型的VaR預測效果，發現高度非線性波動率模型能提供更好的VaR預測。Harvey和Lange（2017）[21]考慮用厚尾分布（譬如，t-分布和廣義誤差分布）來發展GAS模型。淳偉德和趙如波（2016）[22]發現GAS-t Copula模型能夠準確刻畫上證綜指隔夜收益與交易收益之間的非線性時變聯動特征以及相依結構，而姚萍等（2020）[23]綜合考慮了VaR的預測效果與計算負擔，認為基于偏斜t-分布的GAS模型更加合理。

綜上所述，國外學者對市場跳躍行為研究較早，通過加入跳躍因子來構建價格或波動模型（如SV、SVCJ等）并運用于金融市場進行實證的方法已經成熟，而且SVCJ模型在研究跳躍溢出方面具有一定的優勢。國內學者對金融資產跳躍溢出的研究正處于起步階段，在期貨市場涉獵較多，股市之間的研究較少，并且基本都著眼于本國的股票市場，極少將我國股市與其他國家的股市相結合分析。關于跳躍對未來波動趨勢有何影響的研究中，學者們主要運用不同分布的GAS模型對VaR進行了預測。此外，先前大多數相關研究沒有針對特定的突發事件，研究結果未必適用當前的經濟形勢和國際環境。因此，在新冠肺炎疫情沖擊的市場環境下，中美兩國股市的跳躍風險是否存在相互溢出現象，以及由該沖擊造成的跳躍對未來波動有何影響，都值得探究。鑒于此，本文以新冠肺炎疫情在全球蔓延為背景，采用SVCJ模型、GAS模型等對中美股市的跳躍行為進行考察，以期為優化投資策略及政府部門防控公共衛生突發事件造成的資本市場風險提供理論基礎。

與現有研究相比，本文具有以下特色。

第一，國內很少有學者采用SVCJ模型來研究中美股市跳躍行為，該模型能夠很好地描述收益率序列的跳躍式波動。本文基于該模型對跳躍溢出的概率、強度和幅度進行了刻畫和分析。

第二，本文采用由GARCH類模型衍生的GAS模型來研究跳躍對未來波動的影響，是一種較新的做法。對于那些顯著有偏或尖峰厚尾的數據，GAS模型的表現要優于傳統GARCH類模型。

第三，考慮到疫情的影響和模型的穩健性，本文將樣本區間劃分為疫情暴發前期和疫情蔓延時期；考慮到中美時差問題，本文將日收益率劃分為日內收益率和隔夜收益率。

三、研究方法

（一）基于MCMC算法的SVCJ模型

SVCJ模型是一種連續時間框架下的跳躍擴散模型，它假設資產的收益率和波動率都具有跳躍性質，基本形式如下：

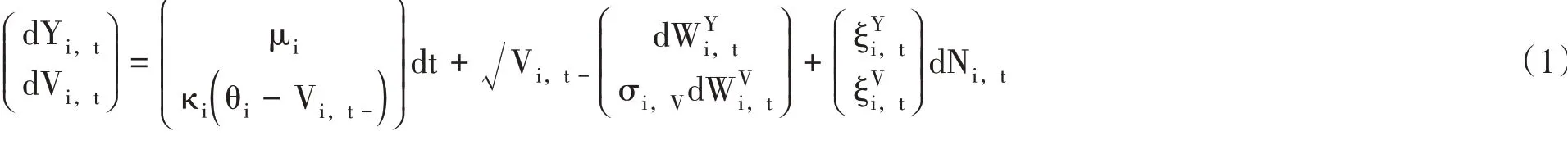
其中，“t-”表示無限接近于t的時間點，Yi，t是第i個資產在第t期的對數收益，Vi，t是第t期的波動率，μi代表期望收益率，ki表示波動均值回復的速度，θi是波動均值回復的平均水平，σi,V用來衡量“波動的波動”。當σi，V較大時，收益率序列存在厚尾性的特征。和表示瞬間相關系數為ρi的標準布朗運動，參數ρi反映資產i的收益率與波動率之間的相關關系。Ni，t服從強度為λ的泊松過程。ξYi，t和分別表示在Ni，t下的收益率與波動率的跳躍項。

當采用貝葉斯的MCMC方法對SVCJ模型進行估計時，要對式（1）進行Euler離散化處理。時間間隔為Δ的離散形式為：

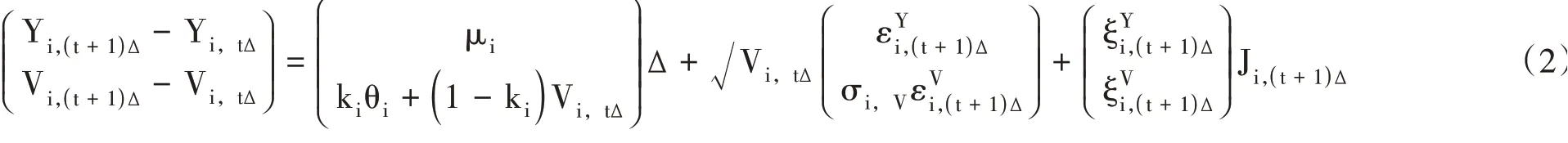
其中，Ji，( t+1)Δ衡量是否實現跳躍，服從強度為λ的伯努利分布，取值0或1。與是相關系數為ρi的標準正態隨機變量，其他參數與原模型同義。

MCMC算法是以貝葉斯模擬為基礎對參數進行估計，克服了傳統模擬方法中高維、靜態等不足。式（2）中存在多個待估未知參數，使用貝葉斯方法“點估計”這些參數的關鍵在于求出聯合分布函數F( V，J，ξV，ξY；Θ)。借鑒宮曉莉等（2018）[13]、劉慶富和許友傳（2011）[12]以及曾昭法和左杰（2013）[24]的做法，本文使用吉布斯（Gibbs）抽樣的方法，以獲得一條收斂的馬爾科夫鏈。

本文重點討論的是中美兩國股市收益率的跳躍溢出效應，故對每個市場存在的隱含跳躍次數J的估計十分重要。借鑒Johannes等（1999）[25]的做法，我們將J的“點估計”定義為：

其中，J（j）代表每次模擬的跳躍概率，M代表模擬跳躍的次數。注意到，J?不是一個由0或1組成的向量，而是在t時刻跳躍到達的后驗估計概率。當跳躍出現的概率小于閾值時不發生跳躍，記為0；相反，發生跳躍，記為1。借鑒Asgharian和Bengtsson（2006）[26]的做法，本文將閾值設定為隱含跳躍和估計跳躍之間的最小平均間隔，它與λ的測算是基本相同的。為了使兩個市場所得出的數據具有可比性，本文采用同一閾值——各樣本λ的平均值。

（二）條件跳躍溢出概率、強度及幅度

基于SVCJ模型及MCMC算法的估計結果，本文依舊借鑒Asgharian和Bengtsson（2006）[26]的做法，采用以下3個指標測度中美股市之間的跳躍溢出效應。

1.條件跳躍溢出概率

條件跳躍溢出概率（CJSP）是指市場之間傳播跳躍行為的可能性，即當一個市場發生跳躍時引起另一個市場在同日或次日發生跳躍行為的概率。若測度美國股市對中國股市的跳躍溢出概率，則選取美國股市作為基準；反之，選取中國股市作為基準。其表達式如下：

其中，同日（次日）跟隨跳躍的次數是指同日（次日）是否跟隨基準市場發生跳躍，若發生記為1次，若不發生則記為0次。

2.跳躍溢出強度

跳躍溢出強度（JSI）是指市場之間傳播跳躍行為的強度，即一個市場發生的跳躍引起另一個市場發生跳躍的程度大小，具體表現為兩個市場發生的跳躍占整個樣本的比重，表達式如下：

3.平均跳躍溢出幅度

平均跳躍溢出幅度（ASJS）是指市場之間產生跳躍溢出的平均幅度。若i代表中國股市，j表示美國股市，則中國股市和同日跟隨其發生跳躍的美國股市的平均跳躍溢出幅度的表達式如下：

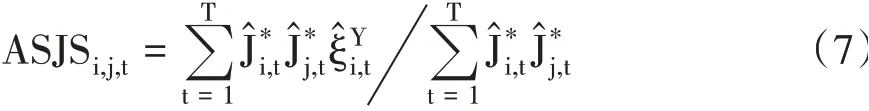
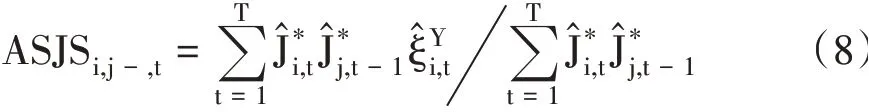
中國股市和滯后一日的美國股市的平均跳躍溢出幅度的表達式如下：其中為中國股市在收益率中的潛在跳躍大小，當時為上跳，當時為下跳。

（三）GAS模型

GAS模型是在GARCH環境下處理跳躍對未來波動率影響的一種方法，它依賴于擾動at的非正態分布和條件方差σ2t=Var（at|It-1）的GARCH型方程。GAS（1，1）模型如下：

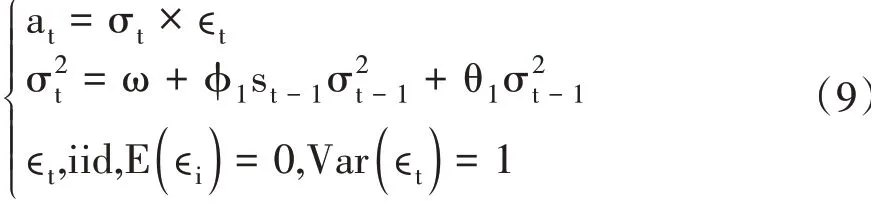
其中，st是條件得分函數，It是直到t時刻的信息集。

如果at服從t-分布，則：

如果at服從廣義誤差分布，則：

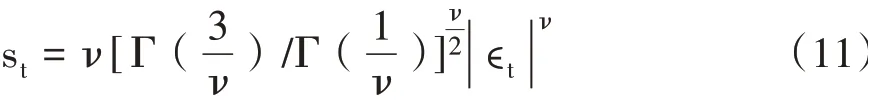
其中，Γ（·）表示Γ-函數。

如果at服從偏斜t-分布，則：

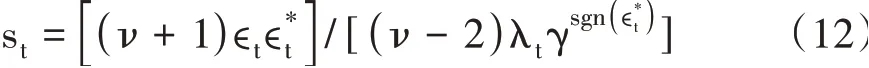
在給定t時刻以及過去信息的條件下，GAS模型可以根據似然度和密度來改善模型的局部擬合，并且能夠較為直觀地更新參數。更值得一提的是，GAS模型的得分分數由完整的密度結構來決定，而并非觀測值的一階或二階矩。這些正是GAS模型與其他觀測驅動模型的不同之處，也是更完善的地方。因此，本文選取GAS模型來測度中美股市跳躍行為對未來波動的影響。

四、實證結果分析

（一）數據

本文選取2017年6月1日—2022年9月19日的上證綜指和標普500指數的日開盤價和收盤價作為原始數據。考慮到兩國的法定節假日差異以及兩市的開盤時差因素，本文剔除了兩市未同時交易的數據，并將日對數收益率分解成日內和隔夜收益率，具體如下：

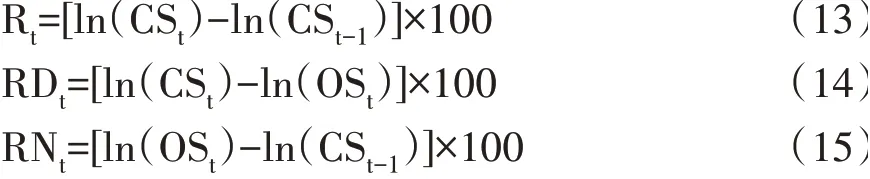
其中，CSt和OSt分別表示第t日的收盤價和開盤價，Rt、RDt和RNt分別表示第t日的對數收益率、日內收益率和隔夜收益率，上證綜指的日內收益率與隔夜收益率分別記為SSRDt和SSRNt，標普500指數的日內收益率與隔夜收益率分別記為SPRDt和

SPRNt。

本文還以2020年1月21日——美國公布首例新冠肺炎病毒感染為時間節點，把全樣本期分為新冠肺炎疫情暴發前期與新冠肺炎疫情蔓延時期，表1報告了基本統計量。由此判斷，在疫情暴發前后以及全樣本時期，均存在中國股市日內收益率大于美國股市以及美國股市隔夜收益率大于中國股市的規律，并且上證綜指日內收益率的均值大于隔夜收益率，而標普500指數正好相反。這些可能與中國股市采用T+1而美股市場采用T+0的交易制度有關。對此，張兵和薛冰（2019）[27]得到過相似的結論，他們認為在T+1交易制度下，中國市場隔夜收益率為負的現象十分穩定。在疫情的沖擊下，上證綜指和標普500指數的日內收益率顯著下降，隔夜收益率卻有所上升。疫情的暴發使中美兩國股市收益率的標準差都有所上升，但因抗疫力度不同，上證綜指標準差上升幅度小于標普500指數，扭轉了疫情前A股市場波動強于美股市場的現象。兩市收益率分布始終呈現有偏、尖峰厚尾特征，J-B統計量的檢驗結果也印證了這一點。此外，由ADF方法檢驗可知，在三個樣本期內，所有收益率序列都是平穩的，這意味著可以直接對它們建模，無須變換。

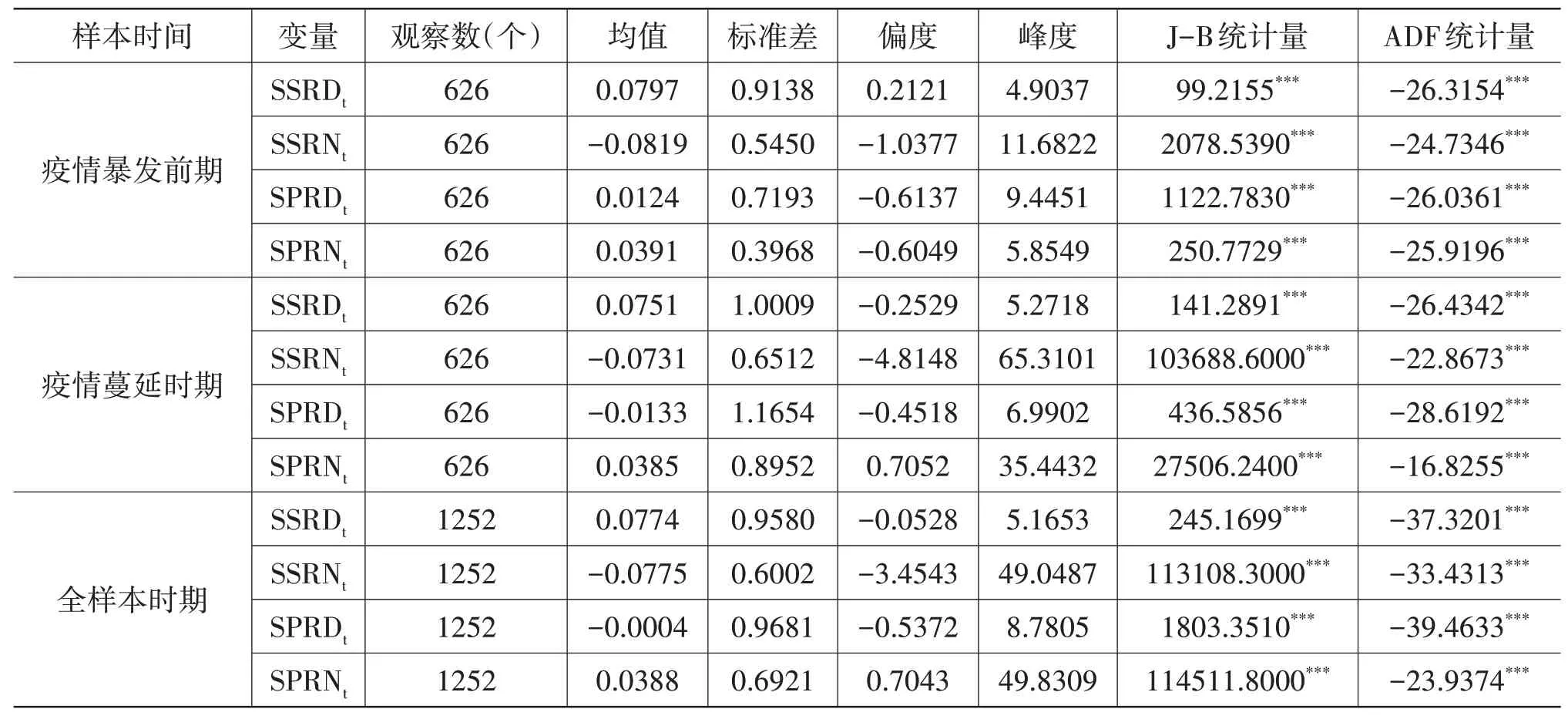
表1 上證綜指與標普500指數日內和隔夜收益率的基本統計特征

為了更加直觀地看出世界前兩大經濟體股市在新冠肺炎疫情沖擊下的波動情況，本文繪制了日內和隔夜收益率時序圖，如圖1和圖2所示。

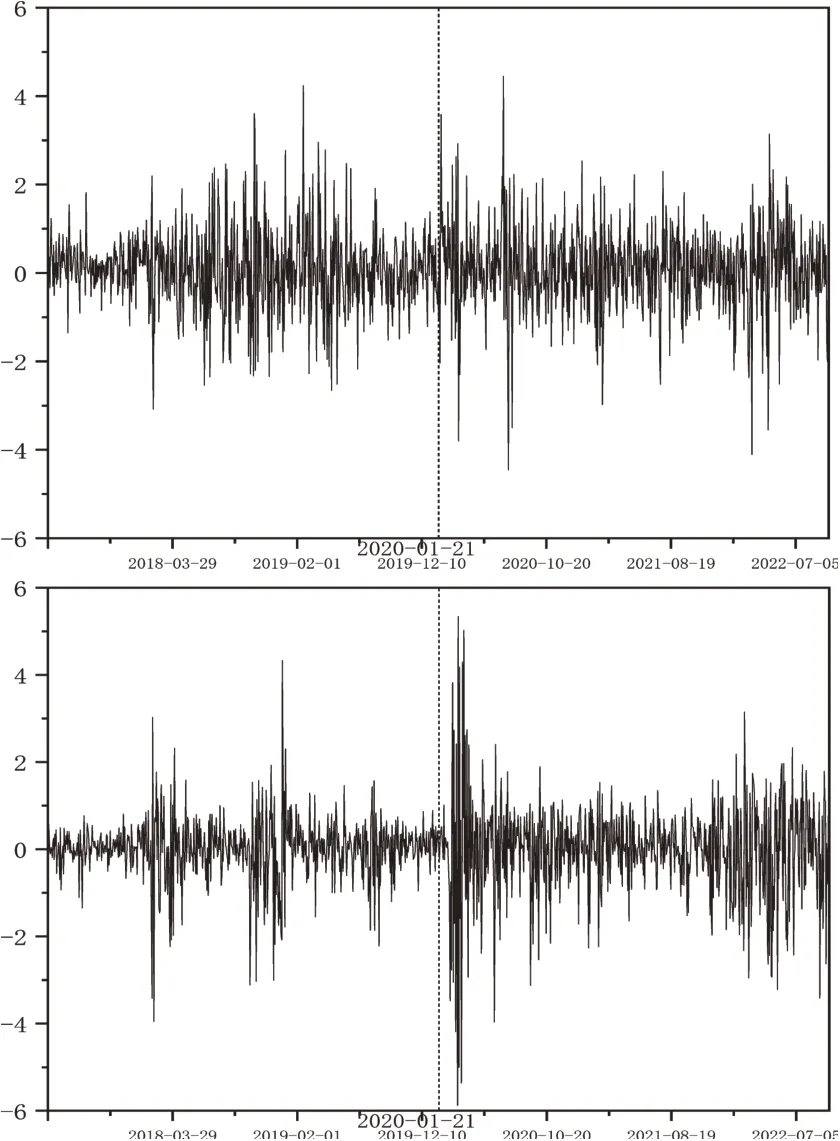
圖1 上證綜指（上）和標普500指數（下）日內收益率的時序圖

從圖1和圖2可以看出，無論是日內收益率還是隔夜收益率，在全樣本期內，中美股市的數據均呈現出聚集性；從波動的劇烈程度來看，隔夜收益率較日內收益率更加平穩；此外，兩市收益率的走勢趨于一致，具有一定的聯動性。疫情暴發之前，上證綜指的收益率波動比較劇烈，尤其是日內收益率，這可能與中美貿易摩擦有關；疫情暴發后，收益率序列出現了劇烈的波動和明顯的上跳與下跳。疫情暴發之前，標普500指數除了貿易摩擦期間存在短暫波動外，其余時間走勢較為平穩；受到疫情的沖擊后，美股日內收益率與隔夜收益率均出現了顯著的劇烈波動。尤其是在美國暴發疫情初期，極端情況更為明顯，這說明疫情確實給美國股市造成了非常嚴重的沖擊。

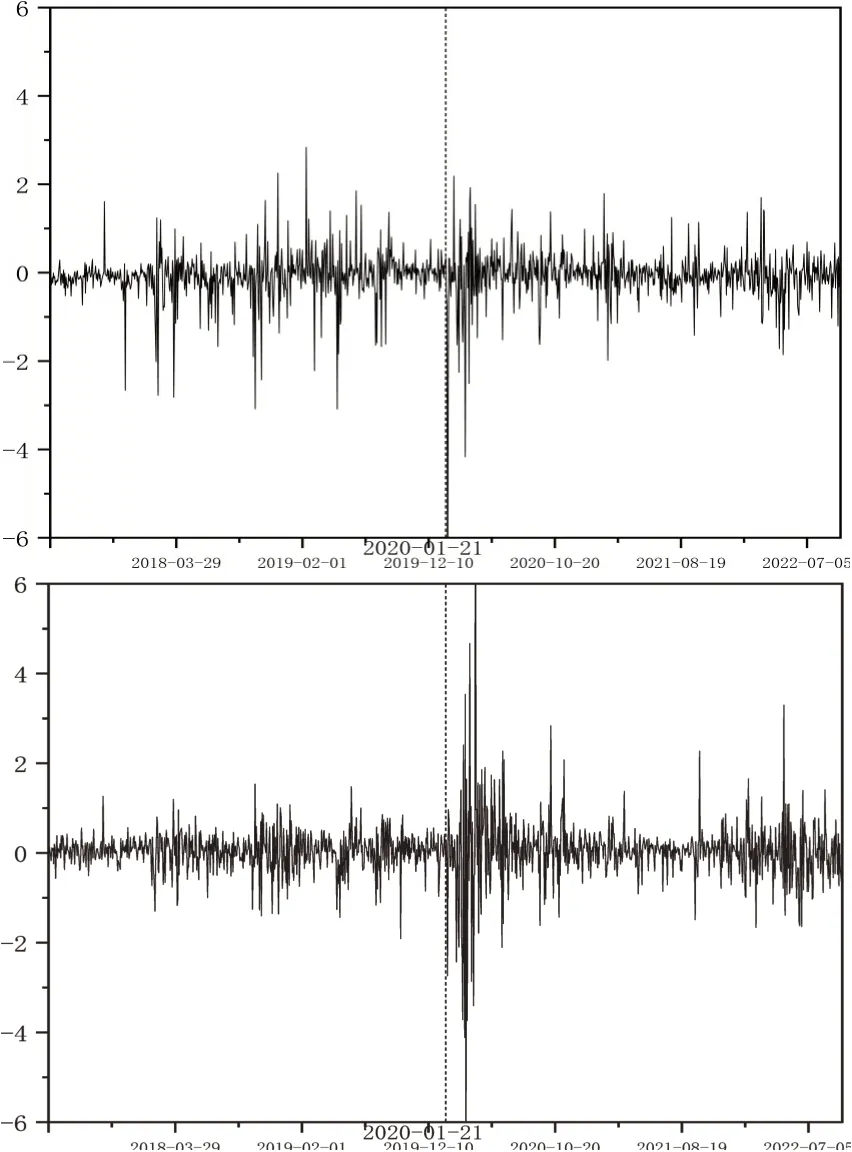
圖2 上證綜指（上）和標普500指數（下）隔夜收益率的時序圖

（二）SVCJ模型的估計結果

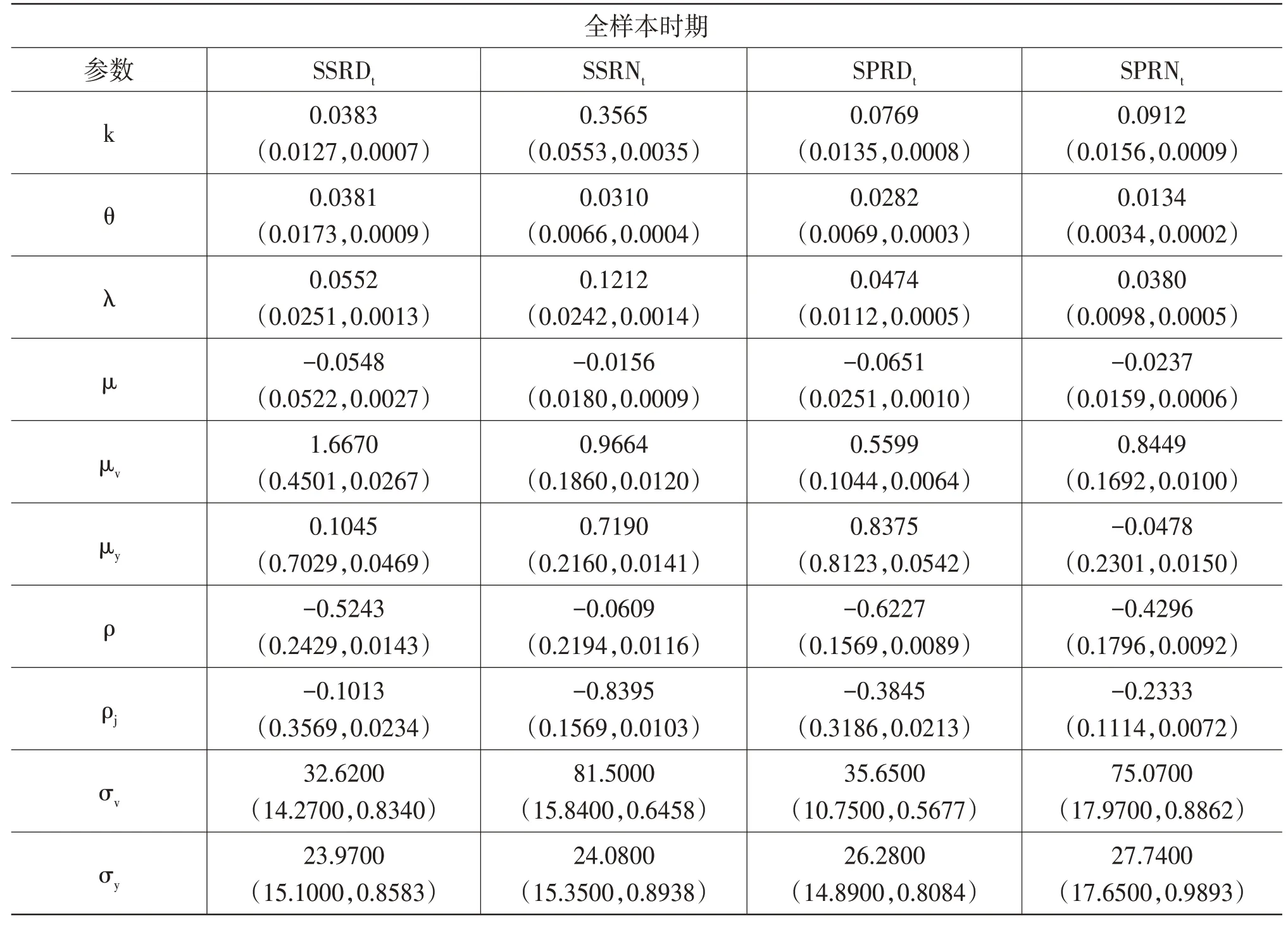
基于MCMC算法估計SVCJ模型，在迭代6萬次，并“燃燒”前面1萬次后所得參數估計結果如表2所示。每個參數的標準差和MC誤差都較小，且樣本路徑圖中所顯示的待估參數抽樣值的走勢與均值基本一致，表明該樣本基本符合馬爾科夫鏈的收斂準則，SVCJ模型擬合有效①篇幅所限，樣本路徑圖沒有展示，可向作者索取。。

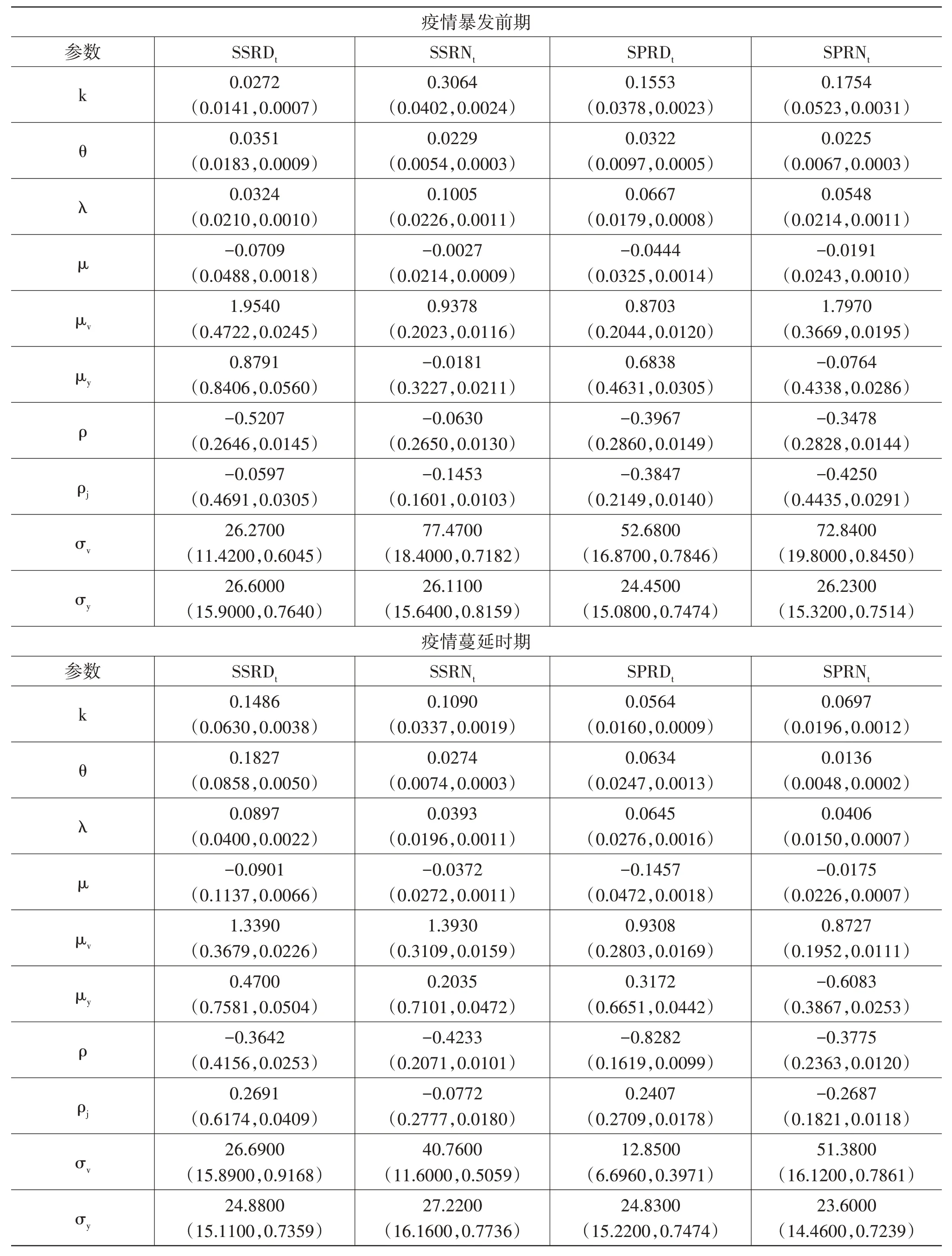
表2 SVCJ模型的估計結果

借鑒劉慶富和許友傳（2011）[12]和Li等（2017）[28]的做法，定義每個市場收益率跳躍的絕對平均幅度為其中，ρj是的相關系數，利用后驗均值估計結果進行計算。在疫情暴發前期，中美股市日內跳躍的絕對平均幅度分別為0.7624和0.3490，隔夜跳躍的絕對平均幅度分別為0.1544和0.8401。在疫情蔓延時期，中美股市日內跳躍的絕對平均幅度分別為0.8303和0.5412，隔夜跳躍的絕對平均幅度分別為0.0960和0.8428。研究發現，在疫情的沖擊下美股市場日內跳躍和隔夜跳躍的絕對平均幅度均有所上升，而A股市場隔夜收益率跳躍的絕對平均幅度明顯低于疫情之前。就跳躍強度而言，根據λ值，疫情暴發前，日內跳躍強度A股市場低于美股市場，隔夜跳躍強度A股市場高于美股市場；而在疫情暴發后，情況完全相反。由此，疫情對兩國股市的跳躍幅度和跳躍強度均有影響，但是對同日和次日的影響結果不盡相同。由ρj的估計值可知，同一市場的收益率與波動率之間幾乎都存在負向的跳躍相關性。三個樣本期的ρ估計值均為負，這表明中美股市各自收益率與其波動率的擴散項之間存在杠桿效應，即利空消息對兩個市場產生的影響要大于利好消息。

續表

（三）跳躍溢出效應測度

由SVCJ模型中J（j）的估計值①篇幅所限，具體估計值沒有在表中呈現，可向作者索取。，結合公式（3），可以計算出疫情暴發前后上證綜指和標普500指數發生跳躍的次數，如表3所示。

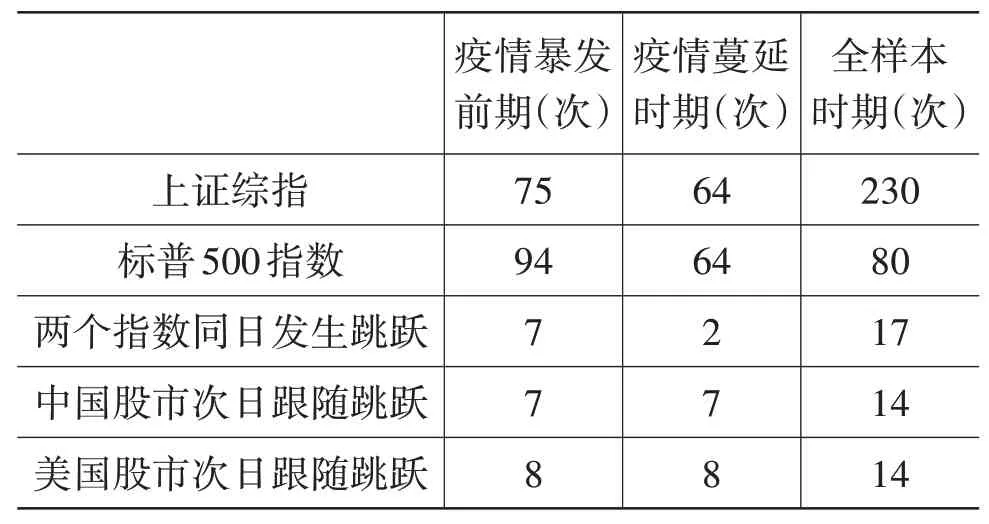
表3 發生跳躍的次數

研究發現在三個樣本期內，中美股市的收益率序列均存在跳躍成分。在疫情暴發前，上證綜指的跳躍次數小于標普500指數；而在疫情的沖擊下，兩者的差距明顯縮小，上證綜指與標普500指數的跳躍次數達到相同水平。雖然疫情發生后兩個市場發生跳躍的次數或多或少有所下降，但是由于疫情暴發前期的樣本里包含了中美貿易摩擦時期，且該時期較長，對疫情暴發前的跳躍次數影響較大，因此不能否認疫情的沖擊會使跳躍行為更容易發生。此外，上證綜指和標普500指數在三個樣本期內次日跟隨跳躍的次數始終持平，有理由相信中美股市之間存在信息互溢的情況，而不只是簡單的單向溢出。于是，接下來可以運用CJSP、JSI和ASJS等指標去測度中美股市之間的跳躍溢出效應。

1.條件跳躍溢出概率

選取CJSP指標測度三個樣本期內中美股市之間的條件跳躍溢出概率。表4展示了同日和次日的溢出概率。

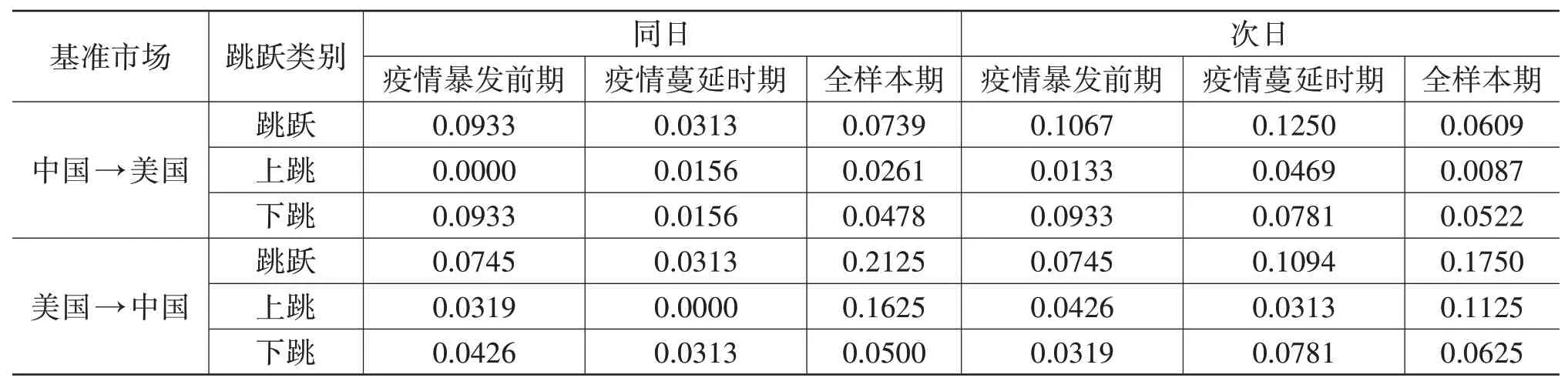
表4 條件跳躍溢出概率（CJSP）

縱向上看，受疫情的影響，無論是中國股市還是美國股市，同日的CJSP都有所下降，而次日的CJSP都有所上升，這意味著疫情暴發后中美股市滯后一天跳躍溢出的概率在增強，相較于疫情暴發前對對方市場跳躍信息做出反應所需的時間變長。另外，美股市場在疫情影響下的次日CJSP顯著大于同日CJSP，這可能是由于疫情后A股市場上最大的活動發生在美股市場關閉的時候。但源自A股市場的跳躍信息的傳遞時效并未受疫情影響，始終是以次日傳遞為主。

橫向上看，以中國為基準市場的CJSP在疫情暴發前后始終高于美股市場，疫情并沒有改變A股市場在中美股市的跳躍溢出概率中的主導地位。子樣本得出的結論與彭選華（2019）[29]得到的結論相似，他認為滬股具有重要的引導作用，美股的風險溢出有限。但是從全樣本看，美股市場更容易引起A股市場發生跳躍現象，中國股市則是處于較為被動的弱勢地位。這與李海超等（2020）[30]得到的結論相同，他們指出A股市場的波動具有明顯的外生性和輸入性的特點，是美股市場沖擊的絕對接受者。

從跳的方向上看，利空消息和利好消息對中美股市的沖擊程度是截然不同的。尤其，在中國到美國的溢出方向上表現出以下跳為主導的不對稱性，這表明源于中國股市的利空消息要比利好消息所引起的跳躍更有可能向美國股市溢出。

2.跳躍溢出強度

選取JSI指標測度三個樣本期內中美股市之間的跳躍溢出強度，表5展示了同日和次日的強度值。

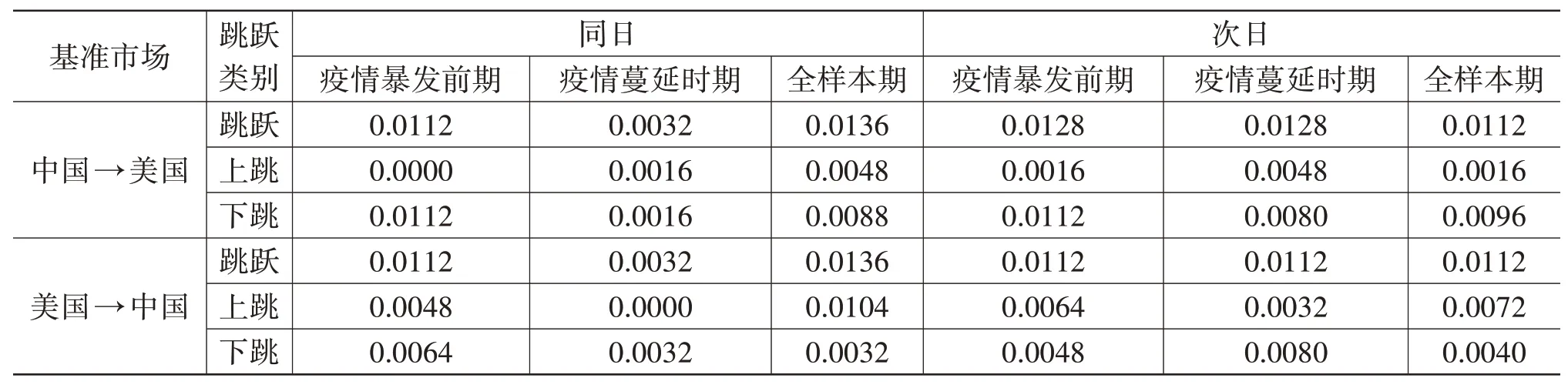
表5 跳躍溢出強度（JSI）

縱向上看，蔓延時期的同日JSI較暴發前期明顯減弱，次日JSI保持不變，疫情減弱了兩國股市在同日引起對方市場發生跳躍的程度，這有可能是疫情蔓延時期兩國的金融、貿易聯系有所減弱導致的。與CJSP相同，不論是疫情暴發前還是蔓延時，次日JSI更大，表現出一日滯后效應。

橫向上看，就同日而言，中美股市對彼此的JSI是一致的；就次日而言，A股市場的JSI略大些。在全樣本中，中美股市的同日、次日JSI都處于同一水平。中國股票市場作為新興市場，卻表現出后來者居上，本文認為這受益于金融自由化程度的逐步加深，中國市場對外的影響力日益明顯，加深了中美股市跳躍溢出強度不相上下的局面。

與CJSP測度的結果一樣，無論是同日還是次日，A股市場對美股市場的跳躍溢出強度存在以下跳為主導的不對稱性。美股市場對A股市場的跳躍溢出強度在不受疫情影響時表現得相對平均，在疫情蔓延時表現出以下跳為主導的不對稱性。這說明疫情暴發后A股市場受到美股市場負面消息影響的程度更深。

研究認為這與疫情暴發后，美國政府沒有及時采取有效的防疫措施，致使疫情在美國不受控制地蔓延，負面消息接踵而至有關。概括地說，美股市場更易受到A股市場利空消息的影響，A股市場在疫情后也表現出相同的不對稱性。

3.平均跳躍溢出幅度

選取ASJS指標測度三個樣本期內中美股市之間的跳躍溢出幅度，表6展示了同日和次日的幅度值。

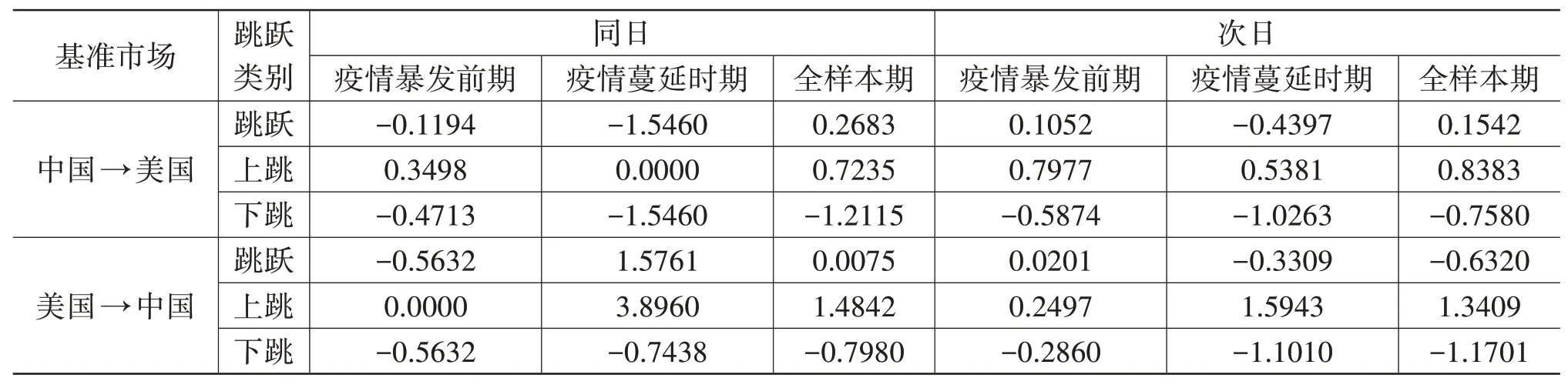
表6 平均跳躍溢出幅度（ASJS）

縱向上看，受到疫情的沖擊，A股市場和美股市場的同日和次日ASJS絕對值均有所上升，這表明疫情加劇了跳躍風險在中美股市之間的傳染。另外，不論是疫情暴發前還是疫情暴發后，兩個市場同日ASJS均高于次日ASJS，信息在當日傳播所引起的對方股市跳躍幅度明顯大于次日傳播所引起的跳躍幅度。這說明信息是具有時效性的，對價格的影響會隨著時間逐步衰退。

橫向上看，疫情暴發前后都表現為：同日美股市場對A股市場的ASJS更大，次日A股市場對美股市場的ASJS更大。換言之，A股市場的跳躍對美股市場的沖擊更緩慢，但美股市場的跳躍對A股市場造成的沖擊會更大。這可能是由于美國股市是信息交流的中心，四面八方的消息都會涌入，而來自中國股市的跳躍信息只是這龐大信息池中的一部分，因此被美股市場完全接收到的時間可能出現延遲。中國股市作為新興市場，很難把精力分散到所有市場，更傾向于關注發達市場的動態，因此對美股市場跳躍信息的反應比較迅速。美國股市已經發展為成熟的國際金融市場，對市場信息的適應力更優，在面對極端風險時，能夠很好地處理來自其他市場的信息沖擊；而中國股市起步較晚，股票市場的價格調整不及美國股市，受到的沖擊會更大。

通過對比上跳和下跳的溢出幅度，發現疫情后A股市場下跳溢出的幅度和美股市場上跳、下跳溢出的幅度均有不同程度的增加，只有A股市場上跳溢出的幅度明顯下降。

另外，疫情還改變了美股市場在疫情暴發前ASJS以下跳為主的不對稱性，疫情蔓延時ASJS表現為以上跳為主。

（四）跳躍對未來波動的影響

經典的ARCH和GARCH模型設定的前提是每個收益率，無論振幅大小，對其未來波動具有相同的影響，EGARCH、TGARCH和GJR-GARCH等模型是對正負擾動賦予不同的權重來考察收益率對未來波動的影響。這些模型都是將所有幅度的擾動考慮在內，沒有區分大小振幅的影響。市場中時常發生的杠桿效應針對的就是大振幅的價格波動（即跳躍），而非一般的價格變化（左浩苗和劉振濤，2011）[31]，杠桿效應的存在說明在考察市場擾動對未來波動的影響時有必要區分大小振幅。基于不同擾動分布的GAS模型能夠有效地測度跳躍對未來波動的影響，其中基于偏斜t-分布的模型還可以捕捉跳躍杠桿效應。

在表3中，本文驗證了新冠肺炎疫情沖擊下中美股市存在跳躍情況，接下來將擬合GAS模型來探索這些跳躍對中美股市未來波動的影響。

對上證綜指和標普500指數在三個樣本期內的日內和隔夜收益率數據擬合ARFIMA-GAS模型，要求at服從廣義誤差分布、t-分布或偏斜t-分布。擬合的充分性由“混成”統計量Q（10）和Q2（10）來判定。關于ARFIMA（p，d，q）的階數，借鑒Cheung和Lai（1993）[32]和Kasman等（2009）[33]的做法，讓p和q在0≤p+q≤2的范圍內變化，由參數估計的顯著性、極大似然函數值以及殘差診斷等來確定最優的（p，d，q）。

關于at的分布，需要做精確的設定，因為它決定著得分函數st的形式。對于上證綜指而言，收益率的γ估計值在三個樣本期都是不顯著的，故先排除偏斜t-分布；然后，比較對數極大似然函數值，發現廣義誤差分布的值始終大于t-分布的值，故選擇廣義誤差分布。對于標普500指數而言，無論是日內還是隔夜，γ的估計值都是高度顯著的，故偏斜t-分布始終優于另外兩種分布。值得一提的是，自由度ν的估計值一直是高度顯著的，這意味著at的分布不可能退化為正態分布。

從式（10）—式（12）中的得分函數st可知，若at服從t-分布，則分子分母中包含的沖擊（?t）幾乎完全抵消，這表明跳躍對未來波動的影響有限且溫和；若at服從廣義誤差分布，沖擊雖有所抵消，但抵消的程度弱得多，這表明跳躍對未來波動的影響是深遠的；若at服從偏斜t-分布，則沖擊的抵消程度介于t-分布和廣義誤差分布之間，跳躍對未來波動的影響是適中的，并且具有杠桿效應。表7報告了最優GAS模型的估計及殘差診斷結果①因篇幅所限，僅報告了ARFIMA模型的階數（p，d，q），其他結果可向作者索取。，從中至少可以獲得以下幾個方面的新發現。

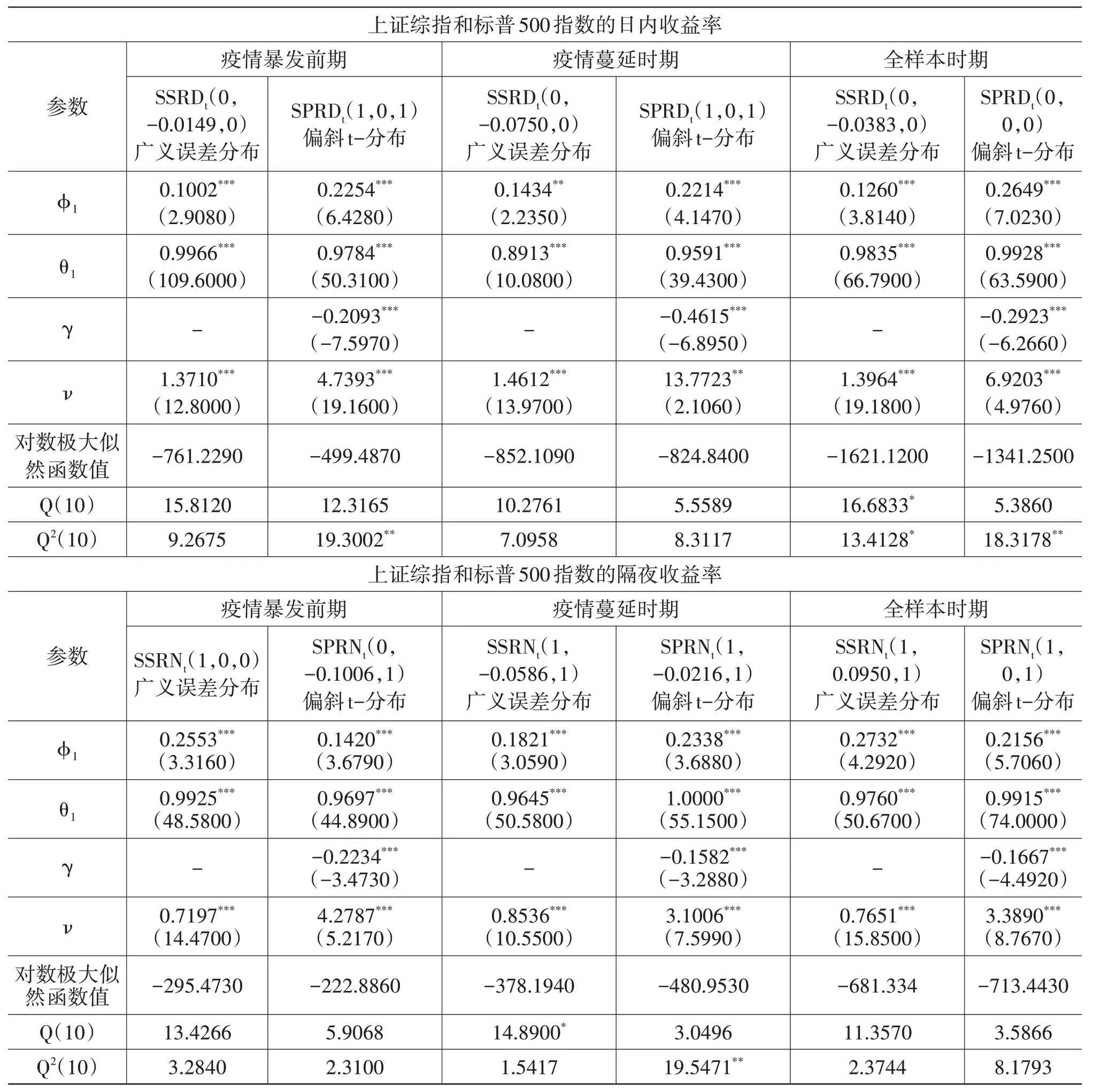
表7 基于廣義誤差分布和偏斜t-分布的GAS模型估計結果

第一，上證綜指在三個樣本期都選取廣義誤差分布，這說明上證綜指出現的跳躍行為對其未來波動的影響是深遠的，每次跳躍都不可能是一個短暫事件，A股市場很難迅速恢復平靜。相比于美股市場，A股市場的有效性較弱，信息在傳播過程中易受到阻礙。

第二，標普500指數在三個樣本期都選取偏斜t-分布，這說明標普500指數發生的跳躍行為對未來波動的影響是適中的，程度低于上證綜指。美股市場是典型的發達市場，全方位發展已經相對成熟。對比A股市場，它是強有效的，因此信息能夠在市場中較快傳播并且很快被消化掉。

第三，根據表7中γ值，可以發現美國股市無論在白天交易時段還是夜晚閉市時段都存在跳躍杠桿效應；而中國股市恰恰相反，在任何時段都不存在跳躍杠桿效應。這鞏固了前人的共識，即普遍認為歐美發達市場均存在杠桿效應，而像中國、巴西等新興市場通常不存在杠桿效應。

第四，疫情暴發前后對分布的選擇是一致的，這說明不管是美股市場還是A股市場，跳躍對其未來波動的影響以及跳躍杠桿效應在新冠肺炎疫情暴發前后沒有發生顯著性變化。

總之，跳躍對中美股市未來波動的影響是客觀存在的，而且有很大差異，但是新冠肺炎疫情沒有改變各自的影響程度。

五、結論與建議

本文基于SVCJ模型測度了疫情暴發前后中美股市之間的跳躍溢出概率、強度及幅度，并運用GAS模型分析了疫情暴發前后中美股市的跳躍對各自未來波動的影響，獲得了一些結論。

第一，中美股市在疫情暴發前后均存在明顯的跳躍成分，且利空消息比利好消息更容易引起股市的跳躍溢出。

第二，中國股市對美國股市的影響力逐漸增強，子樣本中中國股市對美國股市的跳躍溢出概率更高、強度更大，在兩國股市跳躍溢出效應中起主導作用。

第三，中美股市的跳躍溢出概率和強度都存在一日滯后效應。

第四，跳躍的發生對中美兩市未來波動的影響是客觀存在的，而且疫情并未改變這種影響程度，但是中國股市的跳躍對其未來波動的影響更加深遠；美國股市在白天和夜間均存在跳躍杠桿效應，而中國股市不存在跳躍杠桿效應。

在這些結論中，有的鞏固了前人的成果，有的是本文的新發現。

根據以上結論，本文提出以下建議。

一是投資者應該把更多的注意力放在中國股市，不要過度受到美國股市變動的影響。尤其是在發生新冠肺炎疫情之類公共衛生突發事件時，中美兩國抗擊力度不同導致兩國的經濟環境也大不相同，此時更應著眼于本國制定恰當的投資組合，排解美國股市負面消息造成的恐慌。

二是金融監管機構應該提高信息處理的效率，利用一日滯后的時間差，在下一個交易日到來之前盡可能地降低外部沖擊。

三是政府應該加速推動經濟內循環形成，降低對國外供給和需求的依賴性，進而提高對國際公共衛生突發事件的抵御能力。