串列深腔流致聲共鳴特性研究

張正凡，王 鵬，*，王煒哲，劉應征

(1. 上海交通大學 機械與動力工程學院 葉輪機械研究所，上海 200240；2. 上海交通大學 燃氣輪機研究院，上海 200240)

0 引 言

由于流量分配和流動測量的需求以及空間場地限制等，主管路-側深腔（或旁支管）的結構布局廣泛存在于工業復雜管路系統，如核電一回路系統[1-2]、天然氣輸運系統[3]和飛機空氣分配系統[4]等。此時，主管路來流會在腔體開口處發生流動分離而形成剪切渦脫；當剪切渦脫沿著腔體開口處向下游輸運時，一旦與腔體內部固有聲模態達成頻率鎖定和相位匹配[5]，則會發生嚴重的流致聲共鳴現象，從而產生強烈的噪聲輻射，甚至引起結構振蕩和聲疲勞破壞等事故。尤其是對于本文研究的串列深腔來說，上游腔體和下游腔體之間能夠形成聲學放大效應[6-7]，使得內部的聲駐波模態更容易被來流剪切渦脫所激發，從而產生更加嚴重的流致聲共鳴現象。因此，深入研究串列深腔流致聲共鳴產生規律，對于相關管路腔體優化布局及其氣動噪聲抑制等具有重要的理論指導和工程應用價值。

截至目前，國內外已有許多學者針對管路中的單個深腔結構內的流動噪聲現象開展了研究。趙偉等[8]采用壓力傳感器測量了深腔底部壓力脈動的變化規律，發現：流致聲共鳴的發生使得壁面壓力呈正弦波動，并指出流致聲共鳴導致的窄帶噪聲幅值明顯高于由剪切層和湍流脈動引起的寬頻噪聲。East等[9]同樣采用單點壓力測量的方法研究了腔體壓力脈動與來流速度和腔體深度之間的關系，發現：適宜的幾何條件和來流下流致聲共鳴可以被激發，增大來流雷諾數達一定值時，可以激發更高階聲模態，產生更高頻率的流致聲共鳴和壁面壓力脈動；此外，結果還表明增大腔體深度可以減小壓力脈動的窄帶頻率。Hong等利用LES-FWH模型數值模擬方形、圓形和梯形腔體中的流致振蕩，發現方形腔體能夠被激發出最強的聲共鳴，且腔體長深比越小聲共鳴越弱[10]。這些研究揭示了不同管路形狀和流動條件下單個腔體中的聲共鳴現象的變化規律。

在對多個深腔聲共鳴的研究中，Tonon等對多種有雙深腔結構的管道進行了研究，指出若使上游腔體深L2、兩腔間距L3、下游腔體深L4滿足L2=L3(2n-1)/2j=L4(2n-1)/(2i-1) ，i= 1, 2, 3,···；j= 0, 1, 2,3,···；n= 1, 2, 3,···，則發生聲共鳴時的壁面壓力脈動頻率fn=c0(2n-1)/(4L2)，c0為聲速[11]。Tonon等研究了帶有6個不同深度串列腔體的管道，測量了各個腔體端面壓力脈動，發現最強烈的振蕩與同一時刻下僅有一個剪切渦出現在腔口的一階水動力模態有關，同時在6個串列諧振腔中改變部分腔體深度的做法對聲共鳴影響十分有限[12]。Avraham、Tonon等總結了流聲耦合效應的相關理論和機理，提出了一種利用能量守恒預測自激振蕩的模型并將其應用在多種有T形分支的管道系統中[2]。Kriesels等為探究帶有可調深度對稱深腔的管道中的脈動現象，使用渦團法計算二維流場，使用激光多普勒測速儀（laser Doppler anemometry, LDA）、紋影法得到方管中的速度場，測量了圓、方管端部壓力脈動，結果顯示圓、方管的測量結果與計算結果十分相近[13]。

在這多種管道布置形式中，雙深腔串列管道結構的流致噪聲問題得到了部分研究者的關注。Bruggeman等經過理論分析認為發生聲共鳴時的聲波波長λ與側腔深度L存在關系：L= (n+1/2)λ/2 ，n=0, 1, 2, 3, ···，并利用LDA、流動可視化、壓力脈動測量方法研究了有串列腔體的圓截面和方截面管道中的流動，證實了腔體間距為2倍腔體深度時存在強烈的聲共鳴；端面無量綱壓力脈動強度隨腔體長徑比和馬赫數變化，但在低馬赫數下無量綱壓力脈動幾乎與馬赫數不相關；提高當地聲速如采用恰當的擾流板布置，可以將噪聲減小30～40 dB[7]；還提出了一種減小下游腔體前緣的曲率半徑以增強渦脫落的聲吸收作用的方法，指出腔口擾流板的降噪效果取決于輻射和摩擦損失的大小[14]。Ziada等研究了存在聲源激勵、系統壓力0.35 MPa時串列和對稱腔體在一定來流馬赫數下的劇烈聲共鳴現象，認為這種聲共鳴的機制與淺腔中旋渦撞擊腔口下游彎角的振蕩機制不同[15]。

然而，在現有的資料中，很少見到使用管腔壁面多點壓力脈動測量方法參照聲模態計算結果對雙串列深腔流致聲共鳴現象進行研究。本文在計算得到理論聲共鳴頻率的基礎上，對串列深腔流致聲共鳴現象開展聲模態計算和壓力脈動測量，利用聲模態計算獲得了不同腔體間距的管道在各階模態下的壓力時空分布特征，利用動態壓力傳感器陣列得到了不同來流雷諾數和腔體間距下的腔體壓力分布，并將兩者進行對比分析，對串列雙深腔聲共鳴特性隨腔體間距變化的規律進行了探究。

1 研究方法

1.1 聲學計算

1.1.1 固有聲模態

聲波在管道、深腔中傳播時，會在到達一個腔體端面時發生反射。入射波pi與反射波pr相疊加：

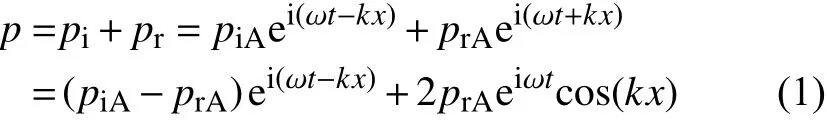
其中：piA為入射波的幅值，prA為反射波的幅值，ω和k分別為該列波的圓頻率和波數，t和x分別為時間和空間坐標。當入射波與反射波能量相近時，第一項幅值遠小于第二項，第二項占主導，因此在距離壁面x=nπ/k=nλ/2 處振幅最大，而距離壁面x= π(2n+1)/(2k)=λ(2n+1)/4 處振幅為零(n為自然數)。聲壓振幅與坐標有關，在管腔中形成了駐波[16]。

在串列深腔中，若要能夠維持自激振蕩，需要駐波模態的駐波波節位于深腔開口的T形接頭處，否則由于T型接頭處空氣振蕩向上下游輻射能量，導致模態不能被激發，于是發生強烈聲共鳴時的聲波波長λn= 2L/(n+1/2)，n= 0, 1, 2,···。n= 0時，有λ0= 4L[7,14]；n= 1時，有λ1= 4L/3 =λ0/3。295 K時，空氣聲速c1=346 m/s，可以計算出一階駐波模態頻率f0=c1/λ0≈540.6 Hz和二階頻率f1=c1/λ1= 3f0，取基準頻率f0=540 Hz對峰值頻率無量綱化。

在特定腔體間距布置下，一定流速的流體流過串列深腔開口能夠激發對應特定聲波頻率f的駐波模態cn。不同模態階數n對應不同波長λ、模態頻率f=c/λ和不同的管腔壁面壓力分布。

1.1.2 聲學有限元

建立管腔結構的幾何模型，在LMS Virtual.Lab中作聲學計算。對所用的管腔模型腔體的上下游管道做了延伸，緊鄰布置上下游管道長都為5.4L，其他布置上下游管道長分別為7.5L、12.5L，其余尺寸與試驗模型相同（見1.2.1節）。

空氣壓力脈動可以分為流動成分與聲壓成分。由于在計算模型中不存在流動，可以將計算得到的壓力場視為聲壓場，即只有聲音成分的壓強時空分布。在給定的管腔結構中，特定波長的聲波可以形成駐波，駐波形成時管腔內聲壓分布關于時間坐標和空間坐標是解耦的，每個位置處的聲壓都以特定幅值和周期做簡諧振蕩。計算得到的聲模態展現了各個不同頻率的駐波及其聲壓分布，聲壓分布為壓力脈動達到峰值時的壓力空間分布。

采用默認的全反射邊界條件，計算頻率范圍為200 ～ 2 800 Hz。取每種串列深腔布置的第一階（C1:f≈f0）和第二階（C2:f≈ 3f0）駐波模態作分析。

1.2 試驗測量

1.2.1 試驗設備與測量方法

使用帶有串列雙深腔的管道作為試驗段流道（圖1），其中腔體寬Dc= 32 mm，管道和腔體垂直于紙面的厚度和主流管道截面高為Dm= 1.25Dc，腔體深度L滿足L/Dc= 5。4種布置的兩深腔中軸之間的間距D1滿足D1/λ=D1/(4L) = 1/16、1/4、1/2、3/4[14]。本文將D1/λ= 1/16的腔體布置稱為緊鄰布置，而將D1/λ= 1/2的布置稱為半波長布置。

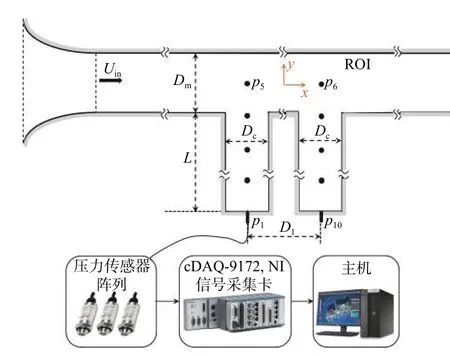
圖1 管道及測量設備示意圖Fig. 1 Schematic of pipeline and auxiliary equipment

試驗段入口上游主管道壁面開有一孔，可以用于測量來流的靜壓，也可以插入畢托管測量入口流速。使用數據采集卡和壓力傳感器實現連續壓力測量。流道側壁共有10個動態壓力測點，每側腔體5個，從腔體端面到腔體與主管道軸線交點均勻排布。4種腔體間距的測點布置相同。測點處壁面開有測壓孔，高靈敏度動態壓力傳感器（PCB，USA）插入測壓孔測得動態壓力信號。信號通過BNC線被傳給采集卡（cRIO-9 039，NI Labview，USA），之后通過USB線被傳給主機并由主機保存測量數據[17-19]。利用預先標定的傳感器系數換算，可以獲得入口靜壓和10個測點的壓力脈動。

空氣在渦聲耦合試驗臺和抽氣泵之間循環，通過穩定段、收縮段和濾網的處理以盡可能接近層流的狀態流入試驗段。試驗前標定風洞內風速，以獲得風機頻率和來流速度的換算系數。

使用腔體間距不同的4種管道布置進行試驗，對每一種布置，在不同入口風速下測定壓力脈動。在特定工況的特定時刻下，由10個傳感器測量到的10個壓力值，可以得到該時刻的駐波波形。

1.2.2 數據處理

為了便于測量聲共鳴發生時的管腔壓力分布并分析其特征，需要選取流致聲共鳴較劇烈的工況，并與聲共鳴較弱的工況相對比。選取壓力脈動最強的測點（由測量結果可知為腔體端面上的測點1、10，實際使用測點1）的數據，繪制無量綱化壓力脈動均方根值pRMS/(0.5ρuin2)隨來流雷諾數Rein=UinDm/v1和腔體間距D1變化的圖象，其中ρ是295 K時空氣在入口靜壓下的密度，v1為295 K下的空氣動力黏度。

從無量綱化壓力脈動時均值變化曲線上選取部分工況作進一步研究。利用FFT變換將壓力脈動信號轉換到頻域上，繪制幅頻曲線。測量時的采樣率為50 kHz，采樣時長大于1 s，故頻域的范圍為1 ～ 25 kHz。通過識別幅頻曲線極值點可以得到壓力脈動的特征頻率，并算出脈動周期。

為刻畫流速隨峰值頻率的變化，將每個腔體間距下的所有工況的峰值頻率各自繪在一張圖中。選取部分工況，繪制一個周期內10個測點壓力的時空分布圖以描述聲共鳴被激發時的壓力時空變化特征，將瞬態壓力p用入口動壓0.5ρuin2無量綱化：p/ (0.5ρuin2)。

2 結果與討論

Peters等[20]指 出，當 腔 體 間 距 為D1=mλ/2 =2mL，m= 0, 1, 2,···， 管道中的駐波模態可以被激發并產生聲共鳴現象。以下詳述D1＜ λ 的4種情形，包括D1=λ/16（緊鄰布置）、λ/4、λ/2 （半波長布置）、3λ/4。

2.1 串列腔體聲學駐波模態

聲模態計算結果為壓力云圖，為獲得一般性的壓力分布特征，用pmax將壓力pa無量綱化（圖2）。

D1=λ/2時，管道的一階駐波模態頻率與理論值非常接近，相差僅1.43%。這里與腔深為λ/4相配套的半波長布置使得駐波波節恰好位于T形接頭處，不會由于T形接頭處的振蕩導致駐波模態能量向上下游輻射，因此能夠維持駐波[14]。

D1=λ/16時，聲模態計算一階駐波模態頻率為489.6 Hz，低于根據二倍深腔深度2L推算的理論值f0約10%；而根據加入腔體間距的駐波波長λ0=2(2L+D1)推 算 的 一 階 駐 波 模 態 頻 率 為=c/λ0≈480.556 Hz，聲模態計算結果與僅相差1.8%。二階駐波模態頻率也存在相同的情況。因此在計算緊鄰布置管腔結構的實際聲模態頻率時需要將腔體間距納入考量。

D1=λ/4 時，一階駐波模態頻率相距基準頻率比緊鄰布置更遠；從圖2中可以看出D1=λ/4時一階模態下向主流管道的行波輻射較為嚴重，其在實際流動中將無法維持駐波。D1= 3λ/4的情形與D1=λ/4相似，由于駐波波節不位于T形接頭處，使得駐波模態因沿管道的能量輻射不能被強烈地激發。

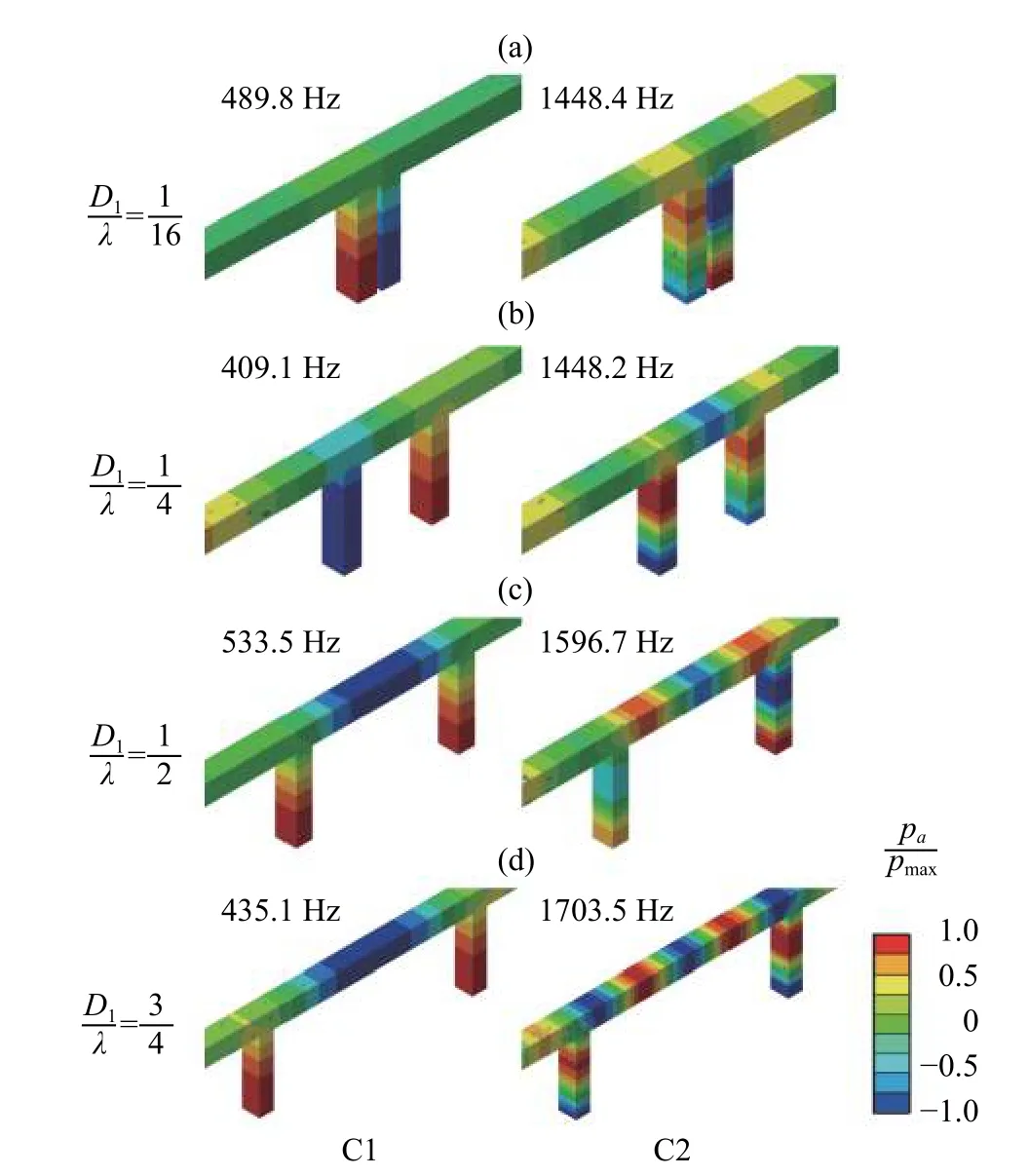
圖2 各腔體間距下的管腔聲模態：(a) D1 = λ/16（緊鄰布置），(b) D1 = λ/4，(c) D1 = λ/2（半波長布置），(d) D1 = 3λ/4Fig. 2 Acoustic modes of tubes with different distances between cavities: (a) D1 = λ/16, (b) D1 = λ/4, (c) D1 = λ/2, and (d) D1 = 3λ/4

此外，注意到一階駐波模態有兩種情形：兩腔體振蕩同相與反相。在D1=λ/16、λ/4時（圖2（a、b）），一階駐波模態表現為兩腔內反相位振蕩；由于腔體之間管道很短，對于波腹位于主管道的駐波模態，腔口的壓力脈動產生向上下游的能量輻射，無法維持自激振蕩，兩腔同相位的駐波模態不會被激發。在D1=λ/2、3λ/4時（圖2（c、d）），一階駐波模態表現為兩腔內同相位振蕩，誘發兩腔間主流管道內反相位振蕩；若其駐波模態波節位于主管道中央，則會導致T形接頭位置的振蕩幅值過大，駐波的能量向上下游輻射，因此兩腔反相位的駐波模態無法被激發。主流管道的波腹處聲壓脈動峰值低于腔體端面脈動峰值，可能與聲波能量沿主管道傳播有關。

2.2 壓力脈動頻譜分析

圖3為4個不同腔體間距的管道中第一個測點即上游腔體端面處的無量綱化壓力脈動隨來流速度的變化。緊鄰布置和半波長布置在一定流速下被激發出了強烈的聲共鳴，而這種現象在另兩種管道中并未出現。

提取緊鄰布置和半波長布置的各個來流雷諾數下的聲壓脈動主頻展示在圖4（a、b）中，其中剔除了環境低頻噪聲占主導的工況，cn=1、2分別表示一階或二階駐波模態被更強烈地激發。將圖3與圖4（a、b）對照，在較大的雷諾數范圍下，聲共鳴主頻與理論值（1.1.1節）很接近，可能是由于緊鄰布置的一階駐波模態被激發，但其腔體間距導致了模態頻率與基準頻率約10%的偏差。從圖3可以看到f≈ 3f0時聲共鳴幅值已經很小，可能是由于高階模態被激發所產生的聲共鳴可以被忽略。

圖3中，半波長布置的振蕩幅值略大于緊鄰布置，這可能是由于緊鄰布置的一階模態的波節不嚴格位于T形接頭處，該處的壓力脈動造成的聲能輻射使其一階駐波模態的能量稍弱于半波長布置。

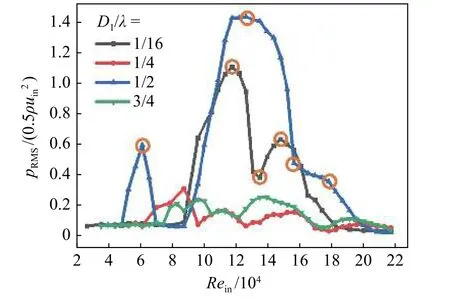
圖3 上游腔體端面的無量綱化壓力脈動RMS值與來流雷諾數的關系Fig. 3 Relationship between the RMS value of dimensionless pressure pulsation at the endplate of the upstream cavity and the inflow Reynolds number

除了存在D1=nλ/2 (n= 0, 1, 2,···) 駐波模態被激發時的頻率鎖定現象外，還可能存在峰值頻率f、來流雷諾數Rein的正相關關系（圖4（a、b））。當D1=λ/4或3λ/4，駐波模態沒有被強烈地激發時，這種相關性更為明顯。D1=λ/4 的結果中St數分布在0.32～0.45和0.66～0.79兩區間（圖4（c）），中位數分別為0.39和0.74；D1= 3λ/4 的St數分布在0.3～0.44和0.65～0.8兩區間（圖4（d）），中位數分別為0.38和0.74；二者的St數均與Bruggeman等所得的StH=(0.4±0.02)(n+1)較為接近[14]，其中St=fDc/Uin。這里可能存在低馬赫數、高來流雷諾數下與腔口剪切層振蕩有關的流體動力學模態或渦脫落模態[14-20]，其模態頻率與來流雷諾數成正比。流體動力學模態的相關情況還有待后續進一步研究。

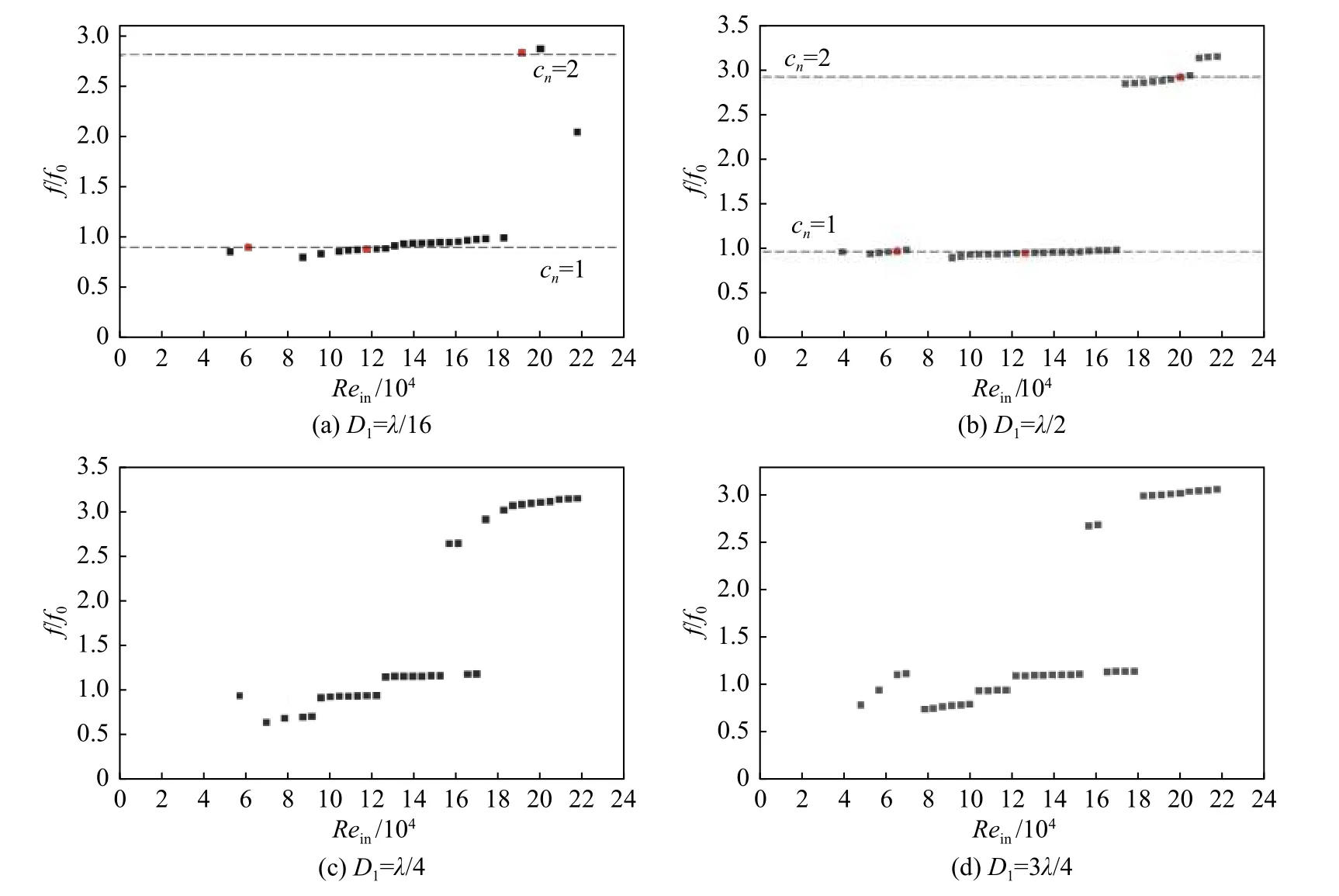
圖4 不同工況下的峰值頻率分布及其對應的模態Fig. 4 Peak frequency distribution under different distances of cavities spacing and acoustic modes

2.3 聲共鳴波形分析

為了驗證管道中發生聲共鳴時其內部壓力分布符合聲模態計算得到的駐波模態結果，這里給出了D1=λ/16和λ/2 的聲模態計算與試驗結果的腔體壓力分布對比（圖5）。分別取圖3中所選工況下幅值最大的相位的壓力測量數據和聲模態計算輸出的數據，并用各自的最大壓力脈動峰值進行無量綱化處理，得到波形對比圖。

兩種布置在所選工況下測得的壓力分布證實了這些工況下所激發的模態均為一階駐波模態。緊鄰布置下聲壓測量與聲模態計算結果吻合較好（圖5（a））。聲模態計算所得壓力在兩腔體間管道的中央幅值為0，并向兩個腔體端面逐漸增大，與試驗結果、理論分析中的n= 1的情形及Ziada等[21]的結論相符，證明了它的有效性。注意到測量數據的左側幅值大于右側，可能與不同的兩腔體流動條件、渦強度等因素有關。

半波長布置下試驗與聲模態計算得到的壓力分布不存在較大偏差（圖5（b））。該布置試驗結果受實際流動中剪切層振蕩、渦脫等可能的因素影響，不是完全對稱的，但對稱性稍好于緊鄰布置。

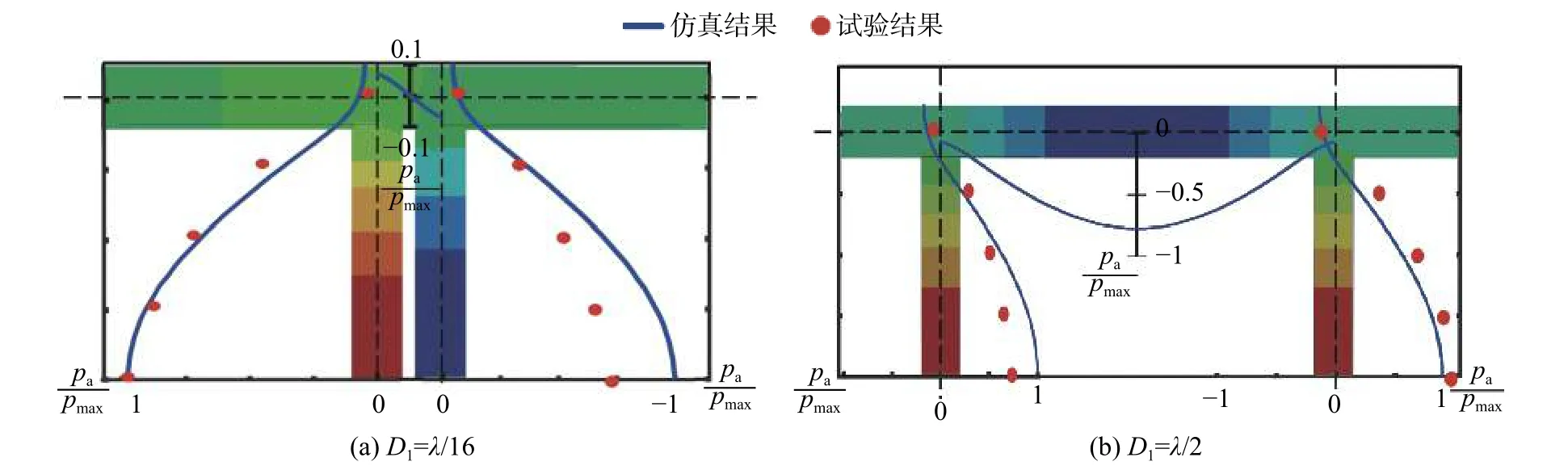
圖5 緊鄰腔體和半波長間距腔體一階模態的測量結果與聲模態計算結果的比較Fig. 5 Comparison of measurement and simulation results of the 1st acoustic mode of the close-proximity duct as well as the half-wavelength duct

由于不同的工況下管道聲共鳴特性可能有較大不同，選取7個工況（圖3），提取這些工況下測得的一個周期內的壁面壓力數據，得到壁面壓力的時空分布圖（圖6、圖7），從圖中可以對這些工況下的腔體壁面壓力脈動特性有直觀了解。

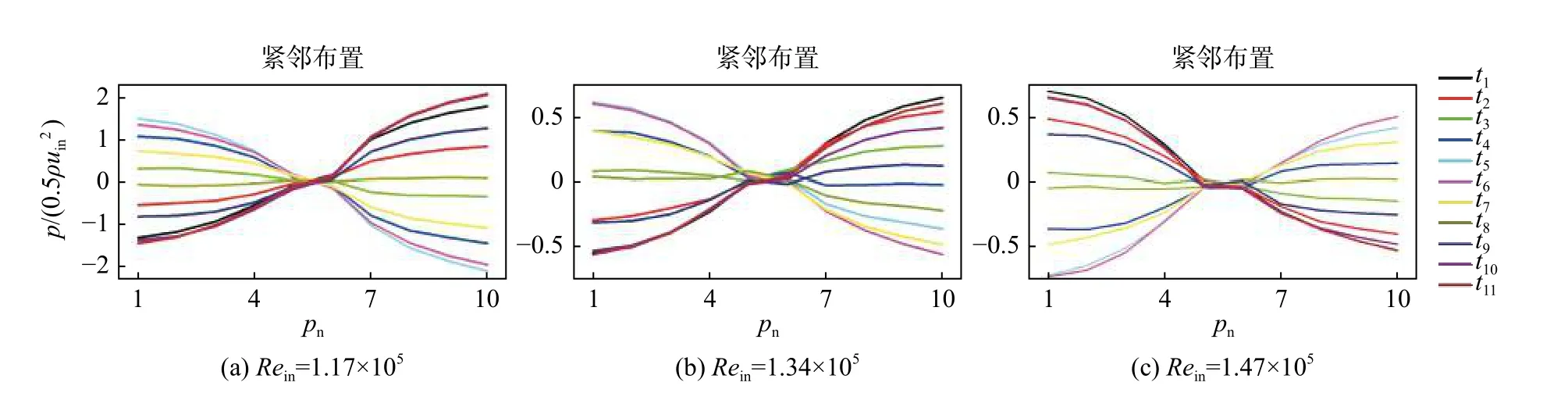
圖6 緊鄰布置下的管壁壓力時空分布Fig. 6 Spatio-temporal evolution of wall pressure at D1≈0

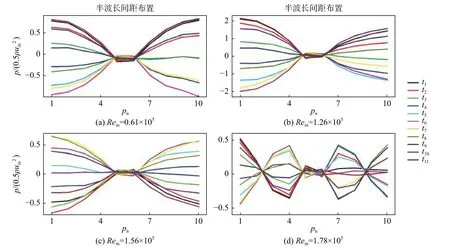
圖7 半波長布置下的管壁壓力時空分布Fig. 7 Spatio-temporal evolution of wall pressure at D1 = λ/2

對于緊鄰布置，隨著來流雷諾數逐漸增大，一階駐波模態被激發，腔體端面壓力脈動不斷增強，在Rein= 1.17×105時最為劇烈，幅值可達2～3倍入口動壓，產生的聲共鳴也十分強烈（圖6（a））；在來流雷諾數繼續增大時，脈動幅值有所降低，在達到入口動壓一半后（圖6（b）），小幅回升并達到一個新的略大于入口動壓一半脈動強度的峰值（圖6（c）），隨后壓力脈動逐漸減弱。在此過程中始終為一階駐波模態占主導，且兩腔振蕩相位相反，波節位于深腔開口附近。

在半波長布置中，隨著來流雷諾數增大（圖3），一階駐波模態被激發，Rein= 0.61×105時出現第一個壓力脈動峰值（圖7（a）），腔體端面壓力脈動幅值接近入口動壓；隨后聲共鳴快速削弱，但在來流雷諾數進一步增大時重新增強并在Rein= 1.26×105處變得十分強烈，壓力脈動峰值達到2倍入口動壓的最大值（圖7（b））；之后壓力脈動快速減弱，但在Rein=1.56×105處脈動幅值約為0.5倍入口動壓時（圖7（c））脈動幅值下降速度放緩；在達到Rein= 1.78×105時脈動幅值仍接近0.5倍入口動壓（圖7（d）），這是二階駐波模態被激發的結果，一階駐波模態已不占主導。一階和二階駐波模態分別在不同的來流雷諾數下被激發并產生強烈的聲共鳴現象，這與緊鄰布置僅一階模態被強烈地激發有所不同。在前兩階駐波模態被激發時，兩個深腔中的振蕩相位始終相同。

3 結 論

本文使用4個腔體間距不同的串列雙深腔的管道模型布置，對不同布置下管道的壓力時空分布進行了聲模態計算，并對各布置在不同來流雷諾數下的管腔側壁壓力脈動進行了試驗測量。試驗得到了各布置在不同工況下的特征頻率，并對比聲模態計算和測量得到的壓力脈動波形、分析幾個不同工況下的壓力時空分布，驗證了所激發的模態為駐波模態，初步揭示了不同腔體間距串列深腔內的聲共鳴規律，主要得到了以下結論：

1）壓力脈動均方根值的變化表明，在合適的腔體間距（半波長布置和緊鄰布置）下，串列腔體內一階駐波模態能夠在較寬的速度范圍內被激發，壓力脈動幅值保持在較高水平，脈動時均值可以超過入口動壓；而二階駐波模態僅在半波長布置下被強烈地激發，其強度弱于一階模態被激發時，但時均值仍可達0.4倍入口動壓。半波長布置的壓力脈動強度最高，其次為緊鄰腔體布置，它們的聲共鳴現象最為劇烈；λ/4、3λ/4間距布置的壓力脈動強度始終在中等或更低水平（10-3～10-1倍入口動壓）。

2）對特定腔體深度和截面下串列腔體間距不同的管道，用不同方法得到了相近的流致聲共鳴模態頻率。利用文獻中給出的聲共鳴頻率計算方法計算了本研究中的腔體聲共鳴的理論一階駐波模態頻率[11]。頻率理論值與半波長布置的聲模態計算結果十分相近而與緊鄰腔體布置有少許偏差；腔體間距非λ/2整數倍的管道不滿足發生聲共鳴的幾何條件，駐波模態不能被強烈地激發，這在實驗中得到了印證。試驗得到的聲共鳴頻率與聲模態計算結果吻合較好。緊鄰和半波長布置在不同的來流雷諾數下被激發出的前兩個聲共鳴主頻分別對應于聲模態計算所得一階和二階駐波模態頻率。

3）壓力脈動時空分布顯示駐波模態被激發時，波腹位于腔體端面，而波節總位于T形接頭處。緊鄰布置的兩個深腔內部聲壓脈動反相位振蕩；半波長布置的深腔聲壓脈動同相位振蕩，誘發主管路聲壓反相位振蕩。聲模態計算結果中主流管道波腹位置的壓力振蕩幅值略小于腔體端面。壓力脈動測量得到的壓力時空分布驗證了聲模態計算的結果。