基于離散優化的飛行試驗點優化設計方法

劉思余，梁 言，馬明明

(中國飛行試驗研究院 發動機所，西安 710089)

0 引 言

飛行試驗是航空科學技術探索和研究的有效手段，是新型飛機研制和鑒定的重要環節，是對航空新型號產品摸索和積累使用經驗的必經之路[1]。由于飛行試驗是一項風險大、復雜度高、成本大的項目，為了降低研制風險，加快研發進度，開展試驗設計在飛行試驗中的應用研究是關鍵措施之一。

以中心復合設計為代表的現代試驗設計方法在航空航天領域有著大量的應用。美國NASA的Langley實驗室[2]在1997年就開始將現代試驗設計方法應用于風洞試驗，國內的中國航天空氣動力技術研究院[3]與中國空氣動力研究與發展中心[4-6]分別針對亞聲速、跨聲速等高速風洞開展了一系列的試驗設計應用研究。試驗結果表明，采用試驗設計方法可以有效地降低試驗資源，提高試驗效率。

Jon[7]將中心復合設計應用于航空發動機進口導向葉片共振頻率試驗，并將中心復合設計試驗結果與全因子試驗進行對比，認為通過試驗設計方法可以得到更精確的物理模型；楊建華[8]采用均勻設計方法進行發動機性能試驗設計，得到的特性規律模型誤差不超過3%；范澤明[9]則采用正交設計方法進行航空發動機高空模擬試驗，獲得各試驗因素對試驗指標影響的顯著性及交互作用；AARON[10-11]與黃陳生[12]等將中心復合設計應用于飛行試驗中，得到了相關試驗科目的規律特性模型。

上述研究均表明了試驗設計在提升試驗效率與試驗結果上的有效性，但也反映了試驗設計中存在的一些共性問題：1）試驗設計過程存在對經驗的依賴，具有一定的主觀性，缺少試驗設計的客觀評價。試驗設計的目的是得到一組試驗點，然后通過試驗點數據得到試驗對象的特性規律模型；該特性規律模型的精度取決于試驗設計好壞，因此特性規律模型的精度的可以作為試驗設計的評價標準；2）試驗對象本身存在使用限制，需要在限制范圍內應用試驗設計方法來安排試驗[12]，但如何在限制條件內尋找一組試驗點，使最終得到的特性規律模型的精度最高是試驗設計需要考慮的問題。

綜上所述，本文針對上述兩個問題進行試驗點優化設計方法研究，通過優化設計方法得到最優試驗點組合集，使最終得到的被試對象規律特性模型精度最高。

1 試驗對象規律模型構造方法

試驗設計需要得到試驗對象的特性規律模型，然后根據該模型進行試驗設計。但在進行實際應用中，試驗對象的特性規律模型可能存在缺失。因此，試驗設計首先需要進行試驗對象規律模型構造方法研究。

多項式模型具有結構簡單、求解方便、計算效率高的特點，可以賦予模型物理意義。試驗設計一般采用多項式模型來反映試驗自變量與因變量之間的規律[2-8,10-15]；由于不同自變量對模型精度的影響不同，可以通過顯著性檢驗量化自變量對模型影響性大小，剔除影響較小的自變量[16]，從而在保證模型精度的前提下簡化模型。因此，本文通過多項式模型與顯著性檢驗方法構造試驗對象規律模型。

1.1 模型顯著性檢驗方法

通過計算樣本數據的總離差平方和SST、回歸離差平方和SSM、剩余離差平方和SSL以及相應的自由度，然后再結合F檢驗就可以判斷模型的顯著性。具體計算公式如式（1～6）所示。其中，dfT是SST的自由度，dfM是SSM的 自 由 度，dfL是SSL的 自 由 度，下標i代表樣本序號。F檢驗具體流程為：計算F=(SSM/dfM)/(SSL/dfL)， 然后將其帶入F(dfL，dfM)計算對應的概率PF。一般PF≤0.05是顯著性可接受的標準。

1.2 自變量顯著性檢驗方法

模型顯著不能表明自變量的顯著性。因此，需要進行偏回歸系數分析以確定不同自變量的影響大小[16]，一般P≤0.05是顯著性可接受的標準。具體方法如下：

1）計算信息矩陣A的逆矩陣C，其中，A=XTX，C=A-1；

2）計算第j個變量的偏回歸平方和Uj，Uj=βj/cjj，cjj為C矩陣主對角線上的第j個元素；

3）計算第j個變量的F值以及對應的概率Pj，Fj=Uj/SSL，帶入F(1，dfM)中計算Pj。

2 試驗設計結果評估方法

試驗設計的目的是獲得試驗對象的特性規律，但不同的試驗點集合會得到不同的數學模型。因此，數學模型能否有效反映試驗對象的特性規律是試驗設計關注的重點。

3 限制條件下的試驗設計方法

對于飛行試驗而言，由于試驗對象、試驗平臺存在使用限制，中心復合設計等試驗設計方法得到的試驗點不能很好地覆蓋全包線；由于實際飛行中飛行條件存在波動，飛行員一般需要試驗點的速度、高度取整，以便快速衡量試驗點執行時的偏差。因此，飛行包線的不規則與試驗點因變量取整是飛行試驗設計的限制條件。

本文通過在飛行試驗限制條件建立試驗點庫，組合不同試驗點生成試驗點組合集，然后以D-最優準則為評估方法，進行試驗點優化設計，得到最有試驗點組合集。

3.1 飛行試驗點庫建立方法

飛行試驗中存在諸多限制，需要根據飛行試驗限制條件建立飛行試驗點庫。具體流程為：1）確定飛行試驗的試驗因子，然后將試驗因子的限制條件轉換為試驗點庫的邊界；2）選取合適的步長建立試驗點庫。

3.2 試驗點組合集編碼

本文的離散優化算法是在遺傳算法的基礎上改進的，替換了遺傳算法中變量的編碼過程，通過組合不同區域離散點序號得到試驗點組合集編碼，具體過程如圖1所示：1）建立試驗點庫；2）劃分試驗點區域，并對區域內的試驗點進行排序；3）依次在不同試驗點區域中選取1個試驗點，按照試驗點區域順序進行排列組合，完成編碼過程。

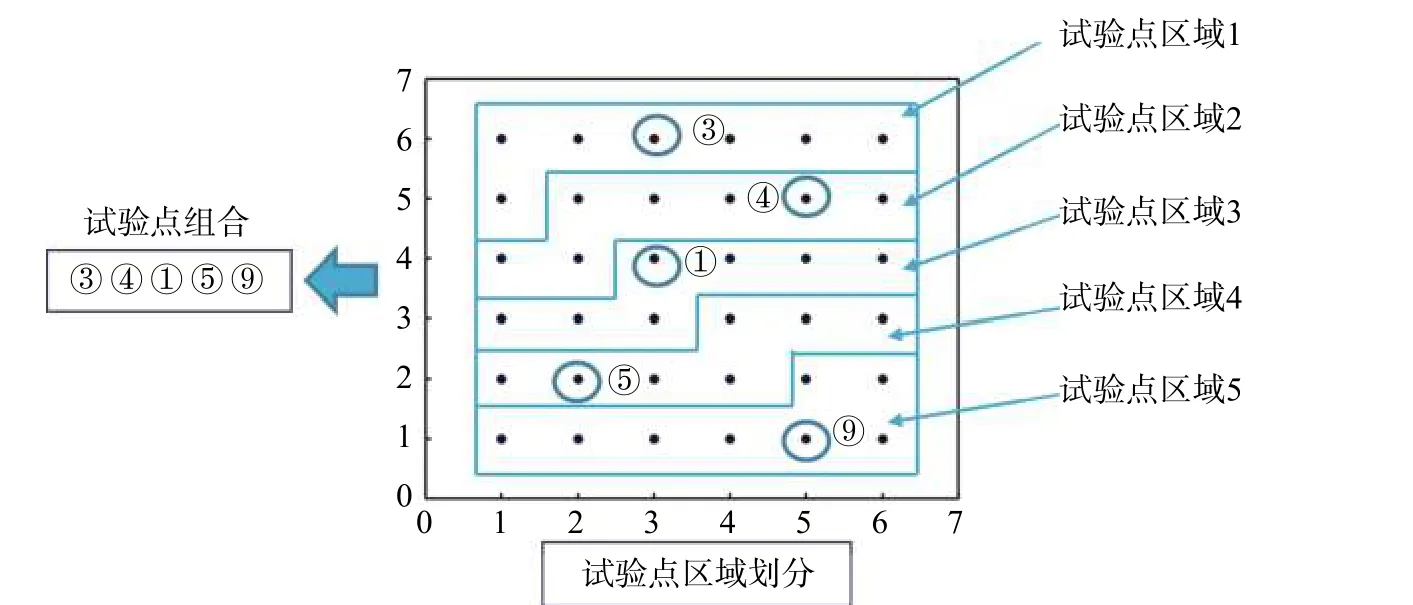
圖1 試驗點組合編碼過程Fig. 1 Encoding process of the test point combination

3.3 離散優化算子

生成新樣本的優化算子分為選擇、交叉、變異三個步驟[17]，具體過程如圖2所示：1）選擇過程：根據樣本適應度選擇父代，個體適應度越大，被選中的概率越大；母代為隨機選擇；2）交叉過程：根據父代/母代中的最大適應度判斷是否進行交叉，適應度越大，交叉的概率越大；若滿足交叉條件，則組合父代和母代的部分編碼片段，得到新樣本；3）變異過程：根據新樣本的適應度判斷是否進行變異。新樣本適應度越大，變異概率越小。

圖2 離散優化算子Fig. 2 Discrete optimization operator

3.4 試驗優化設計

在試驗點數量不變的條件下，離散優化能夠得到該試驗點數量下最優試驗點組合集，但由于試驗點數量的限制，該最優試驗點組合集不一定滿足最終的優化目標。因此，需要增加試驗點的數量，然后在新試驗點數量下重新進行離散優化，直到最優試驗點分布滿足優化目標，具體過程如圖3所示：1）根據試驗點數量n劃分試驗點區域；2）根據劃分的試驗點區域生成編碼長度為n的初始樣本；3）通過離散優化計算最優試驗點組合；4）若該試驗點分布達到優化目標，則優化完成；否則增加試驗點數量，返回步驟1）重新計算。

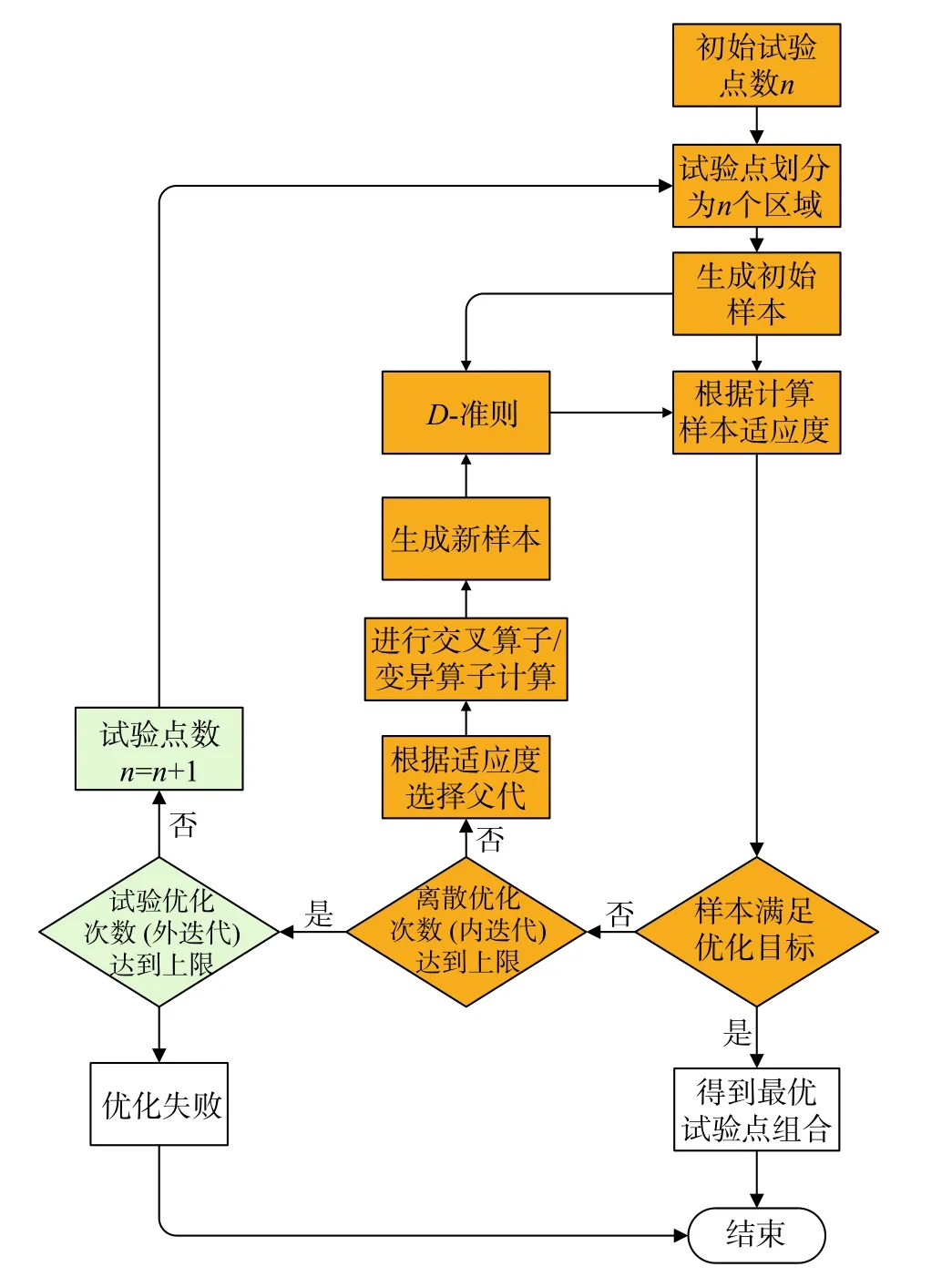
圖3 試驗點優化設計流程Fig. 3 Flow chat of the test design optimization process

4 算例應用

4.1 顯著性檢驗案例應用

本文以某型發動機推力模型進行顯著性檢驗案例應用。首先分析影響發動機推力的試驗因子，然后再對發動機推力數據進行顯著性檢驗，最終得到發動機推力模型。

航空發動機飛行試驗中的試驗因子分為外界因子與內部因子，外界因子包括飛行高度、飛行馬赫數、大氣溫度、飛機過載、迎角、側滑角等，內部因子包括發動機的供油量、尾噴口面積、高/低壓壓氣機轉速等。由于航空發動機飛行試驗一般更為關注飛機平飛狀態下的性能特性，飛機過載、迎角、側滑角等機動狀態參數可暫不考慮。因此，外界因子可只考慮飛行高度、飛行馬赫數、大氣溫度。

航空發動機狀態與低壓壓氣機轉速N1、高壓壓氣機轉速N2、高壓壓氣機出口總壓低壓渦輪出口總溫等多個參數有關，由于航空發動機自身存在特定的控制規律。因此，在外界環境一定的情況下，上述參數中的某一個參數確定，發動機狀態也隨之確定。

因此，對于某型發動機推力性能飛行試驗而言，可以選定4個參數作為試驗因子，分別是飛行高度H、飛行馬赫數Ma、大氣溫度T、燃油流量W或高壓壓氣機轉速N2。一般選取發動機的典型狀態進行試驗，即固定發動機的N2，通過不同飛行條件下的發動機推力數據建立發動機推力性能規律模型。

假設發動機推力模型可以表現為如式（7）所示的3階多項式，根據某型發動機額定狀態的推力數據進行發動機推力模型顯著性檢驗。該發動機與試驗設計所針對的發動機為同一型號系列發動機，構建得到的推力模型在這一型號系列中具有通用性；顯著性檢驗所需數據要較為全面，以保證顯著性檢驗的有效性。根據顯著性檢驗結果依次剔除最不符合要求的變量，直到所有變量的顯著性均滿足Pi≤0.05的要求。最終得到的發動機推力模型變量如表1所示。

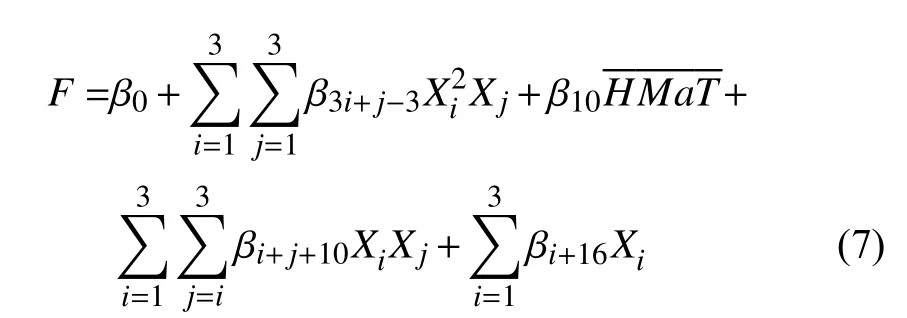
表1 發動機推力模型顯著性檢驗Table 1 Significance test of the engine thrust model

4.2 試驗點優化設計案例應用

本文以某型發動機推力性能試驗為對象，進行試驗點優化設計。根據4.1節中的某型發動機推力模型，再結合各類試驗因子中的限制條件，就可以完成試驗點優化設計。

一般選取發動機的典型狀態進行試驗，即固定發動機的N2，然后在不同飛行條件下進行發動機推力性能試驗。因此，試驗點設計需要考慮的試驗因子為飛行高度H、飛行馬赫數Ma、大氣溫度T。對某機場四季大氣溫度進行統計，統計結果如圖4所示，最終得到的某機場四季大氣溫度規律如圖5所示。某機場大氣溫度限制可根據圖5所示的規律得到；飛行高度H、飛行馬赫數Ma根據飛行平臺的包線進行約束。以上述限制條件作為約束建立試驗點庫，最終得到的試驗點分布如圖6所示。試驗點庫一共包含826個試驗點。

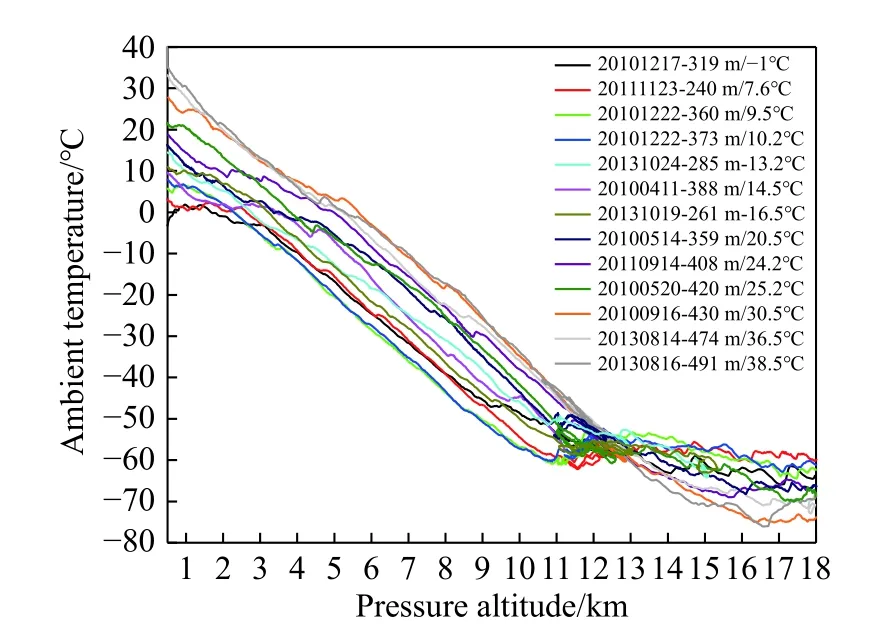
圖4 某機場四季大氣溫度分布統計結果Fig. 4 Ambient temperature statistics of an airport

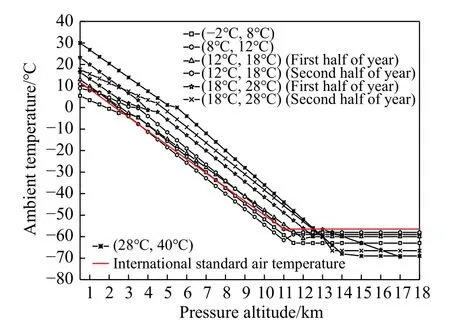
圖5 某機場四季大氣溫度分布統計規律Fig. 5 Statistical law of the ambient temperature of an airport

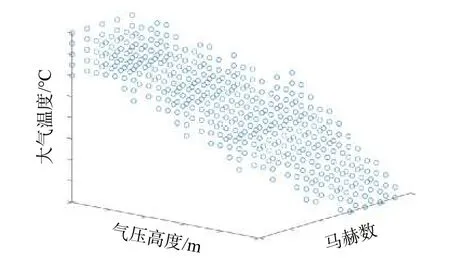
圖6 試驗點庫Fig. 6 Test point dataset

發動機推力模型包含12個模型參數，至少需要12個試驗點才能計算得到發動機推力模型。因此，試驗點初始數量值為12；優化目標為lg(|M|/|M0|)＞4，即最優試驗點組合集的信息矩陣行列式比初始試驗點組合集提高4個數量級。給定試驗點數量后，通過第3.4節中的試驗優化計算方法進行計算。其中，離散優化次數上限值給定為500，優化樣本總數為500。優化過程采用自適應遺傳算法[18]進行計算，以提高算法的尋優能力與收斂速度。

若當前試驗點數量下得到的最優試驗點組合集不能滿足優化目標，則增加1個試驗點，然后再次進行優化計算。優化計算過程中需要注意的是：重新劃分試驗點區域時，需要保證不同試驗點區域所包含的試驗點數量基本一致，否則會引入誤差。不同試驗點數量的優化計算過程如圖7所示，每次計算過程均收斂至當前試驗點數量下的最優解。

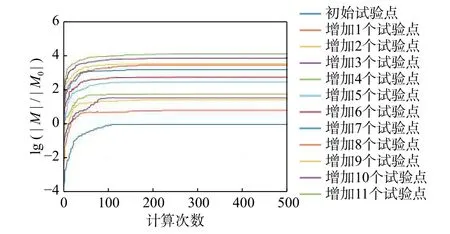
圖7 不同試驗點數量下的優化計算過程Fig. 7 Calculation process for the optimization with different numbers of test points

當試驗點數量增加11個試驗點后，所得到的最優試驗點組合集滿足優化目標要求；最優試驗點組合集優化過程如圖8所示。得到的最優試驗點組合集包含23個試驗點，具體分布情況分別如圖9、圖10所示，所得試驗點均在飛行包線與大氣溫度范圍內。

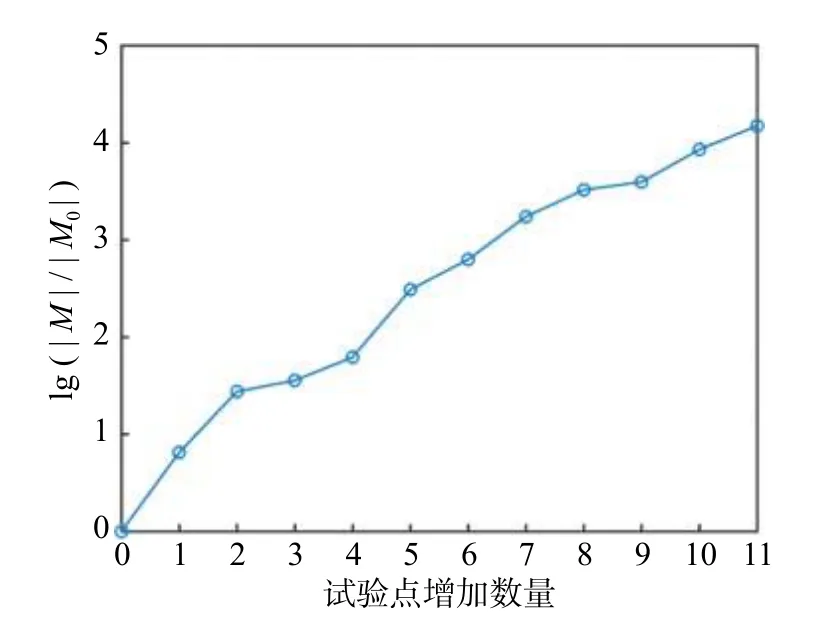
圖8 試驗點組合集優化設計過程Fig. 8 Optimal design process for the test point combination

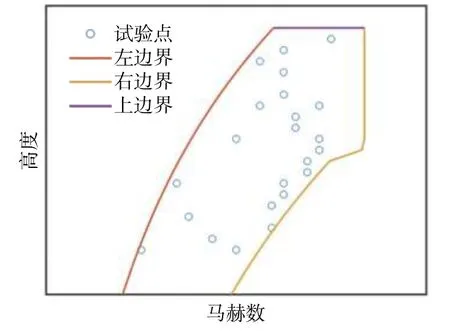
圖9 試驗點組合集優化結果（馬赫-高度面）Fig. 9 Optimal result of the test point combination (Mach-altitude plane)

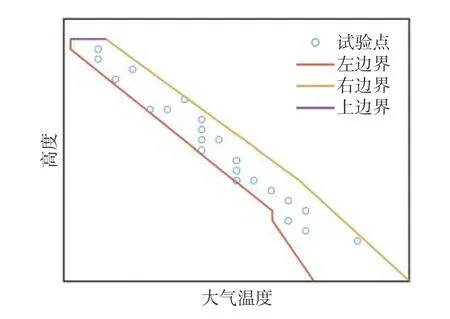
圖10 試驗點組合集優化結果（溫度-高度面）Fig. 10 Optimal result of the test point combination(temperature-altitude plane)

采用某型發動機額定狀態的推力性能計算程序計算得到試驗點數據，該推力性能計算程序已通過某型飛行臺數據進行校正，計算得到的數據具有可信度。根據試驗點數據得到某型發動機額定狀態的推力模型，并對推力模型誤差進行統計，模型誤差計算方法為：（試驗點數據-模型數據）/試驗點數據×100%，誤差統計如圖11所示，大部分模型數據誤差絕對值小于0.5%，僅個別模型數據誤差達到0.8%。

圖11 模型誤差統計Fig. 11 Statistical errors of the model

一般試驗設計會設置驗證點檢驗所得模型的精度[10-11]，本文設置6個驗證點進行模型誤差檢驗。6個驗證點與試驗設計結果中的試驗點不重復，二者為相互獨立關系；驗證點分布于試驗設計空間的不同邊界處，具體分布如圖12、圖13所示。驗證點誤差如表2所示。通過最終試驗點最優組合集得到的推力模型，其驗證點誤差絕對值均小于0.5%。因此，采用試驗點優化設計方法得到的推力模型精度是遠遠滿足工程與科研需求的。

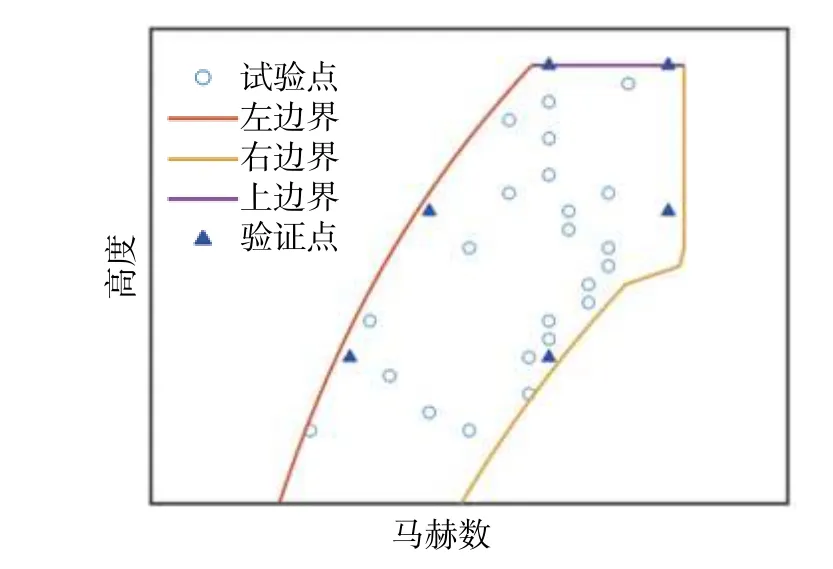
圖12 驗證點分布圖（馬赫-高度面）Fig. 12 Verification point distribution (Mach-altitude plane)

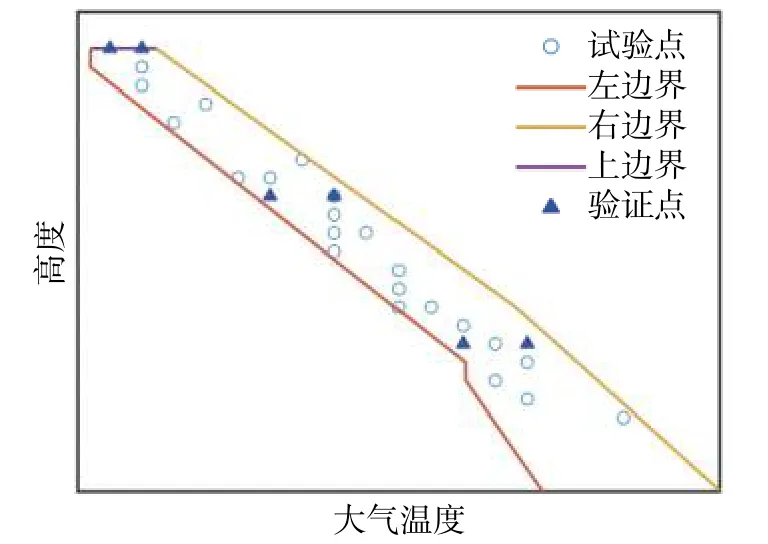
圖13 驗證點分布圖（速度-溫度面）Fig. 13 Verification point distribution(temperature-altitude plane)

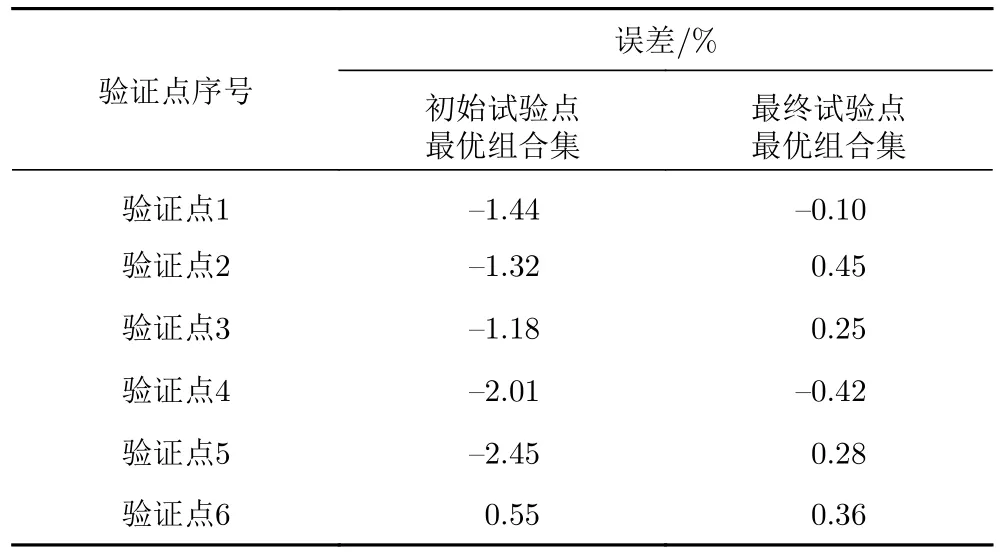
表2 發動機推力模型驗證點誤差Table 2 Engine thrust model errors at verification points

為了對比本文提及的試驗點優化方法的有效性，將初始試驗點最優組合集與最終試驗點最優組合集所得到的模型誤差進行對比，對比結果如表2所示。在6個驗證點中，初始試驗點最優組合集由于試驗點數量的限制，所得的推力模型最大誤差絕對值達到2.45%，而最終試驗點最優組合集得到的推力模型最大誤差絕對值為0.45%。這表明了本文所用的試驗點優化方法的有效性，同時也說明了試驗點優化設計不僅與試驗點的分布有關，也與試驗點的數量有關。

5 結 論

本文基于離散優化進行了飛行試驗點優化設計，采用D-最優準則評估試驗點組合集的優劣，采用自適應遺傳算法算法進行試驗點離散優化，并以試驗點組合的方式取代遺傳算法中的二進制編碼過程，離散優化得到的試驗點是當前試驗點數量下的最優組合集。

以航空發動機飛行試驗為例，最終試驗點最優組合集得到的推力模型最大誤差不超過0.81%，滿足工程使用需求，表明本文采用的試驗點優化設計方法能夠有效地得到試驗點最優組合集，并且試驗點高度、馬赫數為規則的整數或小數，有利于飛行員執行相應的飛行動作。

通過研究發現，試驗點的數量及分布均會影響試驗點設計結果。試驗點數量一定時，試驗優化設計可以得到當前條件下的最優分布，若當前條件下的最優分布不能滿足試驗設計要求，可以進一步增加試驗點數量并重新進行優化設計。本文算例中的試驗點數量由12增加到23時，推力模型的最大誤差由2.45%下降到0.81%。

同時，試驗點優化設計需要根據試驗點的數量將試驗點庫劃分為不同區域。當試驗點試驗點數量增加時，需保證新劃分的不同試驗點區域所包含的試驗數量基本一致，否則會降低試驗優化設計的效果。