借助數學思想方法，解決幾何問題

萬飛

本章是在小學數學“圖形與幾何”知識基礎上的進一步探究，是初中幾何學習的入門知識。下面，我們以幾個常見問題為載體，借助數學思想方法的滲透，幫助同學們更好地攻克本章的幾個難點。

問題一：與線段中點有關的分類討論

例1 在一條直線上有A、B、C三個點，M為AB的中點，N為BC的中點，若AB=a，BC=b，試用a、b的代數式表示MN的長度。

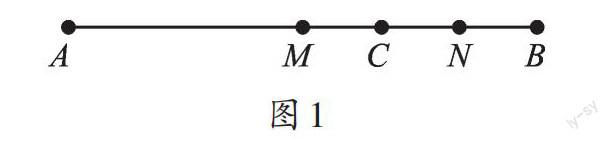
【解析】因為題目沒有給出圖形，畫出線段AB后，點C的位置不明確，所以要分點C在線段AB上、點C在線段AB的延長線上、點C在線段BA的延長線上這三種情況進行討論。

解：①如圖1，點C在線段AB上，MN=MB-NB=?（a-b）。

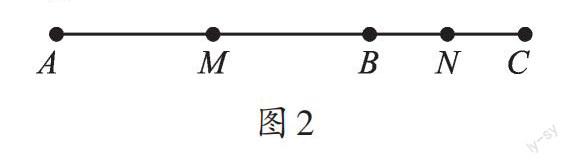
②如圖2，點C在AB的延長線上，MN=MB+NB=?（a+b）。

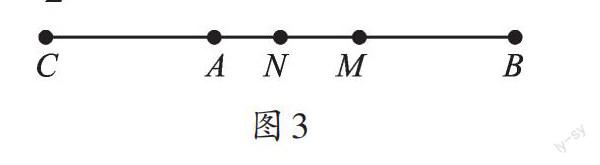
③如圖3，點C在BA的延長線上，MN=NB-MB=?（b-a）。

綜上：MN的長度為?（a-b）或?（a+b）或?（b-a）。

問題二：角度計算中的分類討論

例2 已知∠AOB=60°，∠AOB=3∠AOC，射線OD平分∠BOC，求∠COD的度數。

【解析】本題同樣沒有給出圖形，因此不知道OC在∠AOB內還是∠AOB外，所以需要分類討論。

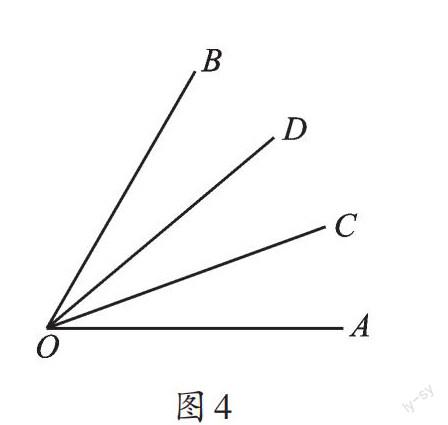
解：①如圖4，OC在∠AOB內，此時，∠BOC=∠AOB-∠AOC=60°-20°=40°，所以∠COD=?∠BOC=20°。

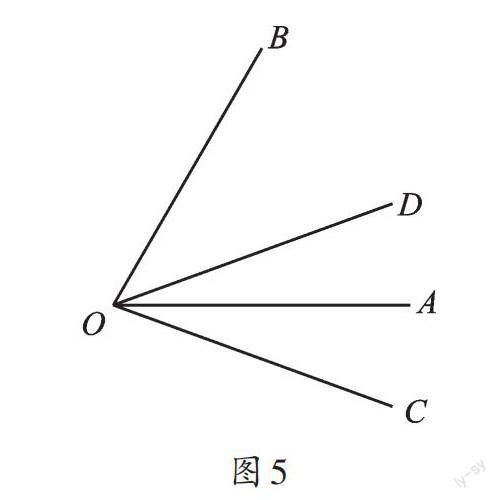
②如圖5，OC在∠AOB外，此時，∠BOC=∠AOB+∠AOC=60°+20°=80°，所以∠COD=?∠BOC=40°。

綜上：∠COD的度數為20°或40°。

在沒有給出圖形的題目中，一般會有多種情況，需要分類討論。上面兩題可放在一起用類比的思想進行研究，難點在于怎樣準確地畫出所有圖形。

問題三：互余、互補概念辨析

例3 下列說法中，哪些是正確的？請說明理由。

（1）互余且相等的兩個角各是45°；

（2）一個角的余角一定小于這個角的補角；

（3）如果∠1+∠2=∠3，那么∠1的余角與∠2的余角的和等于∠3的余角；

（4）如果∠1+∠2=∠3，那么∠1的余角與∠2的余角的和等于∠3的補角。

【解析】（1）45°+45°=90°，正確；

（2）設這個角為α，則它的余角為90°-α，補角為180°-α，補角比余角大90°，正確；

（3）∠1的余角為90°-∠1，∠2的余角為90°-∠2，∠1的余角與∠2的余角之和為180°-∠1-∠2=180°-（∠1+∠2）=180°-∠3，錯誤；

（4）由（3）的解析可知結論正確。……