生活中的平移實例剖析

汪二梅

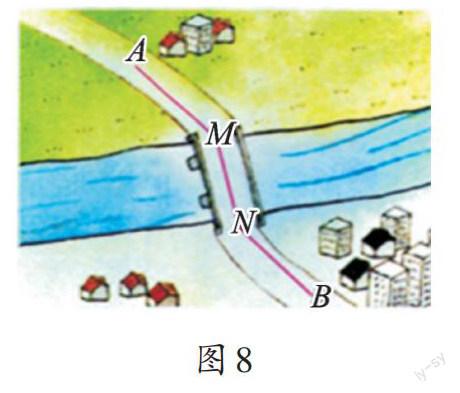
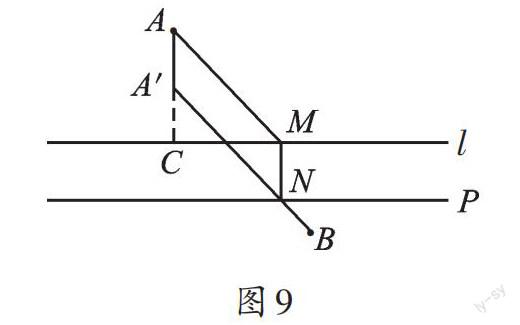
數學源于生活，又應用于生活。生活中處處有平移，恰當地利用平移變換來解決數學問題，往往可以起到事半功倍的效果。

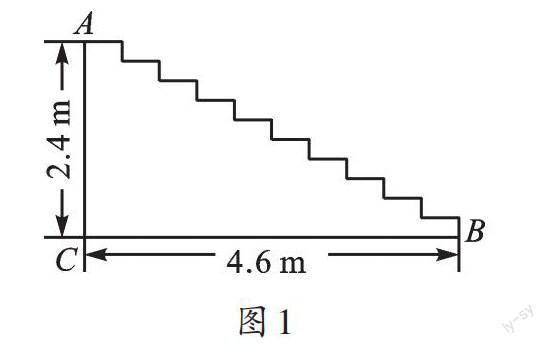
例1 如圖1，中央商場重新裝修后，準備在大廳主樓梯上鋪設某種紅色地毯。已知這種地毯每平方米售價30元，主樓梯道寬3m，其側面如圖1所示，則購買地毯至少需要多少元？

若要通過逐步計算，比較復雜。我們可以先利用平移的知識，將樓梯水平方向的線段沿豎直方向分別平移到BC上，豎直方向的線段沿水平方向分別平移到AC上。于是，鋪地毯的橫向線段的長度之和就等于橫向直角邊的長度，縱向線段的長度之和就等于縱向直角邊的長度。所以，地毯的總長度至少為4.6+2.4=7（m），總面積為7×3=21（m2），所以購買地毯至少需要21×30=630（元）。

我們運用平移的知識，把要求的所有線段平移到一條直線上進行計算，問題就變得容易多了。因此，同學們在學習平移知識時，一定要用心去體會。

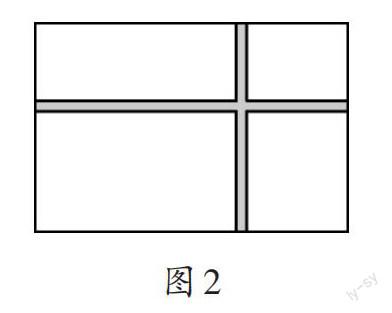
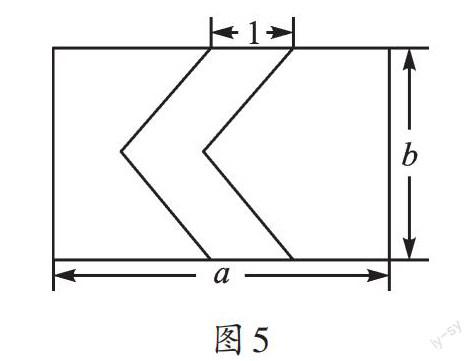
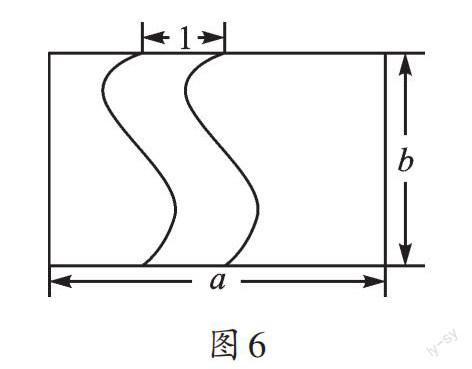
例2 如圖2，在寬為20m、長為30m的長方形花園中，要修建兩條寬為1m的長方形道路，余下部分進行綠化，請求出綠化部分的面積。

同學們常用原大長方形的面積減去兩個小長方形（即兩條道路的面積），再加上一個邊長為1m的小正方形的面積求解。

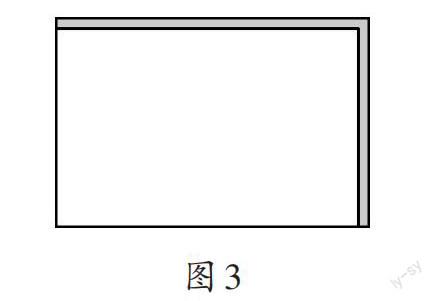
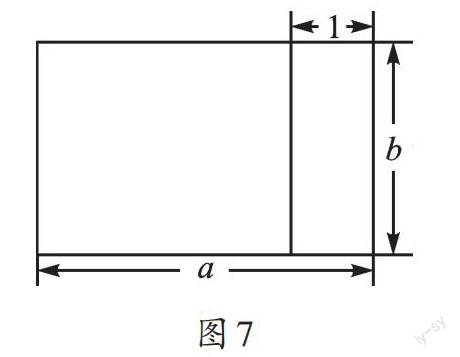
但上述過程比較復雜，如果應用平移，則簡便許多。具體做法是：將兩個小長方形（即兩條路）分別平移到長方形的上邊和右邊，即把分散的內容集中到一塊兒，讓計算簡單化，如圖3。這里通過平移變換，避免了對圖形的分割，使求解更簡潔、方便。……