負阻態憶阻Hopfield 神經網絡動力學

劉益安，馬瑞辰，李 國，于 奇，劉 洋，胡紹剛*

(1. 電子科技大學電子科學與工程學院 成都 611731；2. 電子科技大學重慶微電子產業技術研究院 重慶 高新區 401332)

生物神經網絡擁有大量的神經元(～1011)以及突觸(～1014)，并且彼此之間形成錯綜復雜的連接，是一個龐大的非線性網絡系統。研究表明，人類大腦的運行機制與神經元和神經網絡的動力學行為密切相關[1-2]，而且已被證實大腦中存在混沌現象[3]。為了揭示大腦的工作機理，神經網絡動力學行為研究成為人工神經網絡領域的重要內容，而憶阻器具有集成度高、可模擬突觸可塑性、非易失性等特點，被認為是最有潛力的神經形態器件[4]，并且其良好的非線性是研究人工神經網絡動力學的重要條件。

1971 年，文獻[5-6]發現了第4 種基本元件，即憶阻器，其阻值可變且保持記憶功能。2008年，惠普實驗室研制出首個憶阻器件[7]，后續產生了大量關于憶阻器的研究成果[8-10]。雖然惠普憶阻器模型作為使用最廣泛的憶阻模型之一[11-12]，但推導一個完全表征惠普憶阻器的數學模型是一項具有挑戰性的任務[13-14]。因此，將非線性二次模型和三次模型等簡化模型用于憶阻器電路的理論定量分析[15-16]，會導致許多應用的結果不能令人滿意。為了緩解這個問題，文獻[17]提出了一種新的非線性對數模型來表征憶阻器，文獻[18]提出了具有負阻態功能的憶阻器模型，能夠更加準確地模擬突觸可塑性和非線性脈沖激勵神經元功能。

目前關于憶阻器神經網絡的研究涵蓋了廣泛的主題[19]，其中憶阻Hopfield 神經網絡(Hopfield neural network, HNN)表現出豐富的動力學行為，并在解決組合優化問題和圖像復原領域具有優勢[20-23]。1990 年，文獻[21]首次將混沌引入HNN，開啟了HNN 豐富的動力學行為研究。2011 年，文獻[24]將憶阻器引入HNN，并利用嚴格的數學證明分析了網絡的動態行為，并以兩個神經元數值實例進行了驗證。2014 年，文獻[25]利用憶阻器替換HNN 的一個權值，構建了一個3 神經元的簡單網絡，使得網絡表現出準周期軌道、混沌以及超混沌等復雜的動力學行為。2016 年，文獻[26]將憶阻器三次方數學模型帶入HNN，并通過相軌圖、龐加萊映射圖和Lyapunov 指數對網絡的動態特性進行研究，獲得了不存在平衡點的超混沌吸引子。2020 年，文獻[27]利用一種耦合雙曲線憶阻器等效電路來模擬HNN 的突觸串擾，并在不同串擾強度下觀察到HNN 的多重穩定性、不對稱吸引子和反單調性。

本文在前期提出的具有負阻態功能的憶阻器模型基礎上，為了更好地模擬突觸可塑性以及增加網絡的負反饋功能，構建了基于憶阻器的新Hopfield神經網絡模型，并對網絡動力學行為進行了分析研究。實驗結果表明，提出的憶阻Hopfield 神經網絡模型具有豐富和復雜的動力學行為，為后續該神經網絡在模式識別、數據處理、圖像加密等方面的研究打下了堅實的基礎。

1 具有負阻態的憶阻器模型

1.1 憶阻器模型

由憶阻器的初始定義可知，它是滿足 φ ?q域特定關系的一種器件，但為了進一步豐富憶阻器的內涵，文獻[6]又提出了廣義憶阻器的概念，即一個憶阻系統的定義應該滿足如下關系：

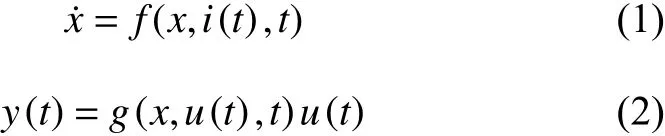
式中，u(t)和y(t)分別為系統的輸入信號和輸出信號；x為系統的n階狀態變量；g為一個n維的連續向量函數；t為時間。

磁通或電壓控制型憶阻系統的關系可寫成：

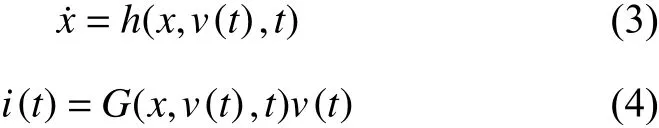
式中，h為一個n維的連續向量函數。此時的憶導值G也不再僅由磁通量 φ決定，而是由狀態變量x、輸入電壓v以及時間t共同決定。

由上述定義可知，廣義憶阻器將影響憶阻值的變化因素增多了，本文提出的改進模型就是對狀態變量x進行了有效調整，使憶阻器能夠呈現出正負兩種阻態，消除了對理想憶阻器電導極性的限制。

如圖1 所示，新憶阻器模型可以視為夾在兩個金屬電極之間的厚度為2D的半導體薄膜，包括一個正電導區和一個負電導區(每個區的厚度為D)。它也可以視作兩個理想憶阻器背靠背連接，一個具有正電導，另一個具有負電導。憶阻器的電導由狀態變量x確定，并且x的調控范圍從原理想狀態憶阻器的[0,D]擴展到[?D,D]。

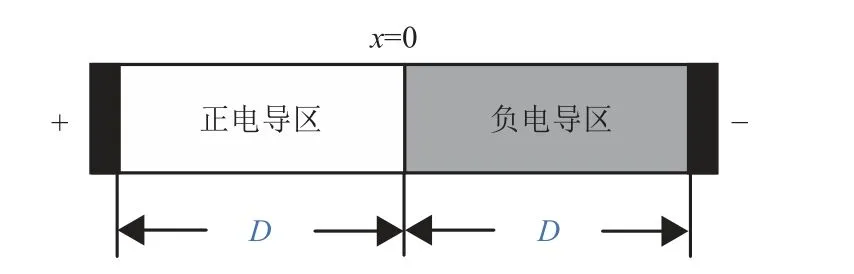
圖1 憶阻器模型物理結構圖

假設只考慮最簡單的歐姆電導情形，G(x)定義為與狀態變量x成正比，即G(x)=ax，其中a是常數系數。同時在實際憶阻器使用中，特別是氧化物類憶阻器，其兩端的電阻或者電導經常會隨著時間的推移而逐漸降低，所以可以通過引入衰減項(bx)模擬這種阻值變化，其中b為衰減系數。綜上所述，改進的憶阻器可以描述為：

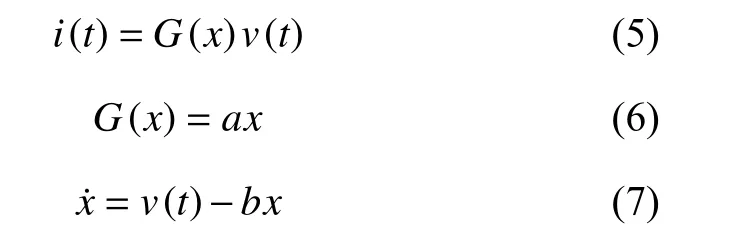
除了兩個端點?D，D外，狀態變量x與通過憶阻器的磁通量成正比。在改進的憶阻器模型上施加外部電壓，可以使x的位置發生變化，從而改變憶阻器電導的大小與極性。如假設a=1 且b=0，如果在憶阻器上施加正電壓，x向陽極移動，電導可能處于正阻態，反之若施加負電壓，x向陰極移動，電導就可能處于負阻態。

1.2 器件模型仿真

當對改進的憶阻器施加一個正弦電壓v(t)=Asin(ωt)時，可以得到憶阻器的電導公式為：

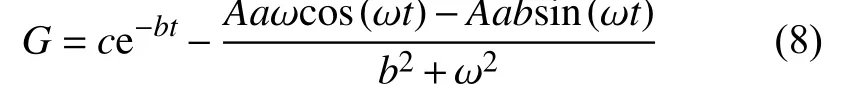
式中，c是常數系數；A、ω 分別為正弦電壓幅度、頻率。設置c=1，A=2，ω=2π，x0=?0.5，相關測試結果如圖2、3 所示。若b=0，即忽略衰減項，通過繪制電流與電壓的關系，可獲得呈水平8 字狀的捏滯回線，I-V曲線跨越所有4 個象限，且主要在2、4 象限，與原理想憶阻器模型僅在1、3 象限的斜8 字I-V曲線相比具有明顯不同的特性，也意味著所提出的憶阻器模型具有負電導。此外，若b=0.08 時，施加正弦電壓，可以獲得多個連續的穩定狀態。

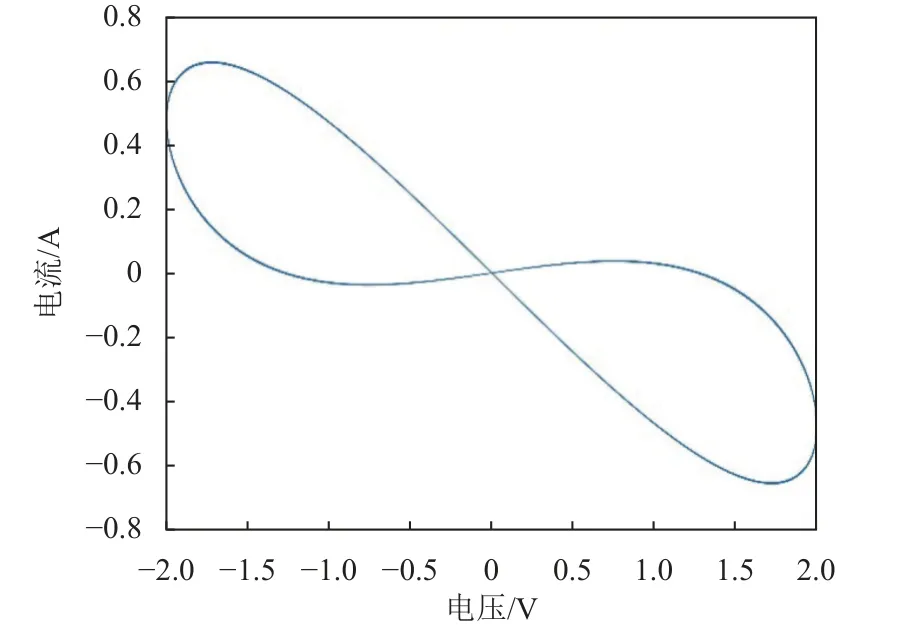
圖2 憶阻器電流電壓曲線圖(a=1, b=0)

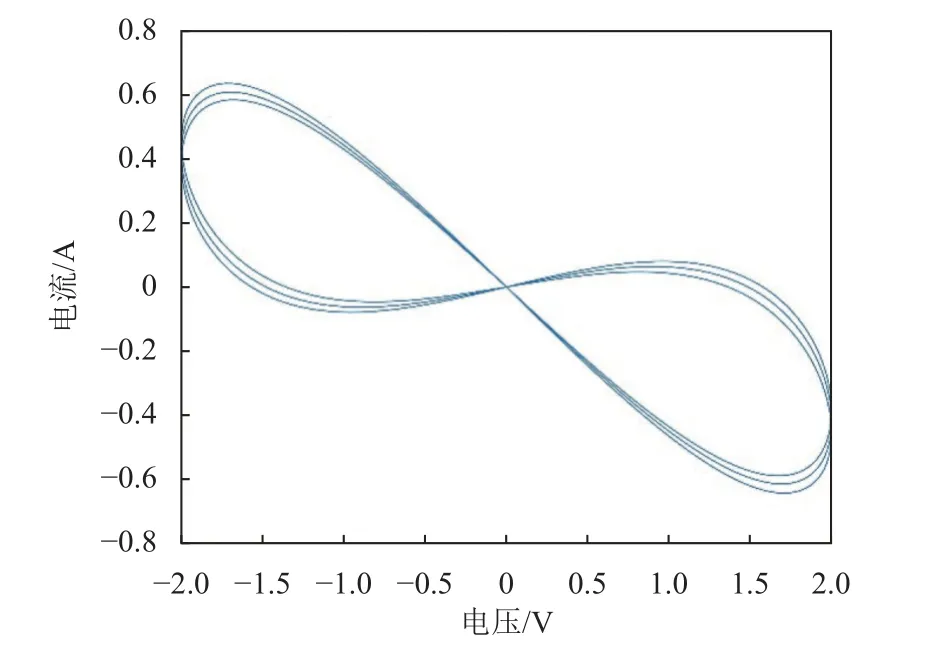
圖3 憶阻器電流電壓曲線圖(a=1, b=0.08)

2 憶阻Hopfield 神經網絡

選取3 個神經元的連續型Hopfield 神經網絡[28]，表達式為：

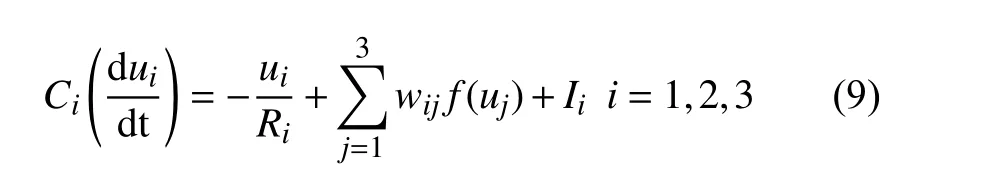
式中，Ci為 第i個神經元的輸入電容；ui為第i個神經元的輸出變量；Ri為第i個神經元的傳輸電阻；wij為 神經元的連接權值；f(u)為神經元激勵函數；Ii為神經元外部激勵。為簡化計算過程，通過單位歸一化后，設置Ci、Ri均為1，Ii為 0，f(u)為雙曲正切函數，即f(u)=tanh(u)。

Hopfield 網絡是一種全連接的反饋型神經網絡，每個神經元與其他所有神經元相互連接，3 神經元HNN 需要9 個突觸連接權值。憶阻器本身具有阻值記憶特性，是良好的突觸仿生器件，以往的憶阻器基本只有正阻態，而反饋型神經網絡，特別是混沌神經網絡，往往需要負反饋權值。由于憶阻器的電導與權值具有相同的量綱，可以將具有負阻態的憶阻器替換HNN 的一個權值，新憶阻Hopfield神經網絡表達式為：

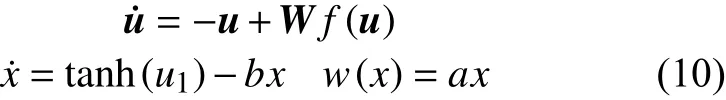
式中，u為輸出變量矩陣；W為連接權值矩陣。可以表示為：

由式(10)、(11)可知，新網絡的演化情況由系統初始值、權值矩陣W以及憶阻器參數a、b確定。

3 網絡動力學特性分析

首先基于實驗室24 核48 線程AMD 3960X 服務器平臺，使用粒子群算法，搜索新HNN 模型比較優化的參數配置。設置a=1，b=0.05，初始值u(0)=(0.1,0.1,0.1)，W權值矩陣為：

系統仿真時間為500 s，時間精度為1 ms，各參數采用國際標準單位歸一化，無量綱。如圖4 所示，系統的相位軌跡圖呈現出普通的單渦卷吸引子，但單純從相軌圖還不能判定是否為混沌系統，還要結合Lyapunov 指數的正負情況。根據式(10)求得系統的Jacobian 矩陣，再利用施密特正交化方法，求解系統的Lyapunov 指數[29]。如圖5 所示，系統最終的Lyapunov 指數分別為LE1=0.012 5，LE2=?0.003 4，LE3=?0.068 5，LE4=?6.891 2，存在大于零的Lyapunov 指數，所以可以初步判定系統達到混沌狀態。

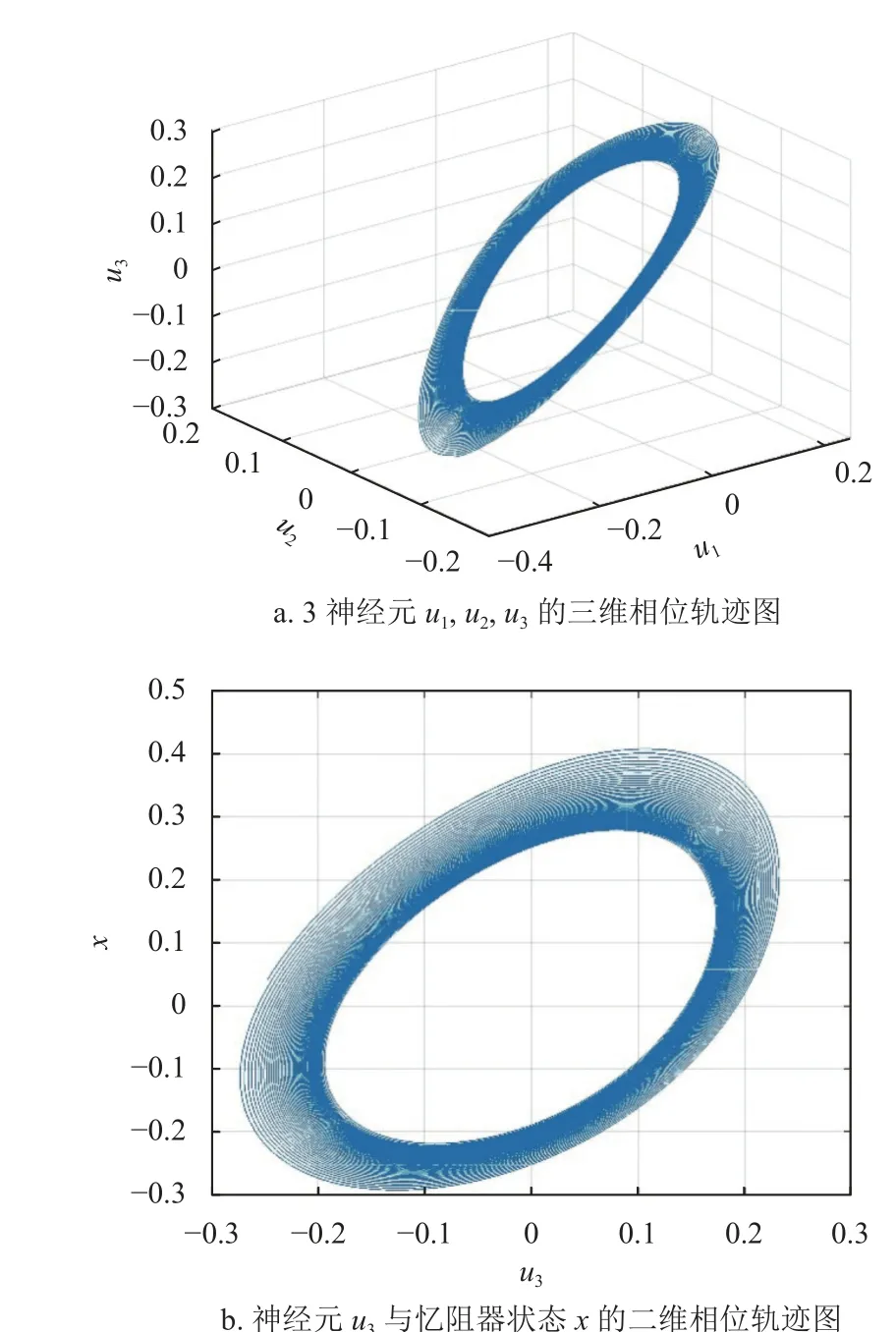
圖4 系統的相位軌跡圖

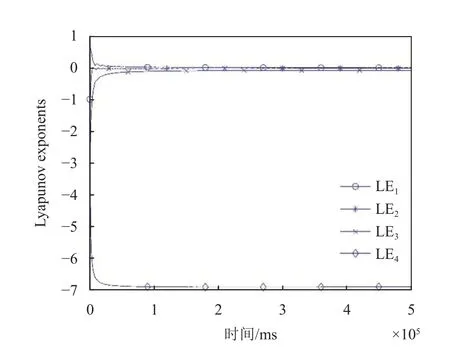
圖5 Lyapunov 指數圖

3.1 憶阻器參數的影響

通過調整憶阻器參數a，b的值來觀察憶阻器對系統動力學行為的影響。如圖6 所示，其他實驗條件不變的情況下，a取[0.5, 1.5]，步長為0.01，當a從0.50 增加到1.09，系統的Lyapunov 指數變化不大，LE1、LE2、LE3在零附近，LE1始終略大于零；當a從1.09 增加到1.50，系統的Lyapunov指數發生較大變化，且都小于零。

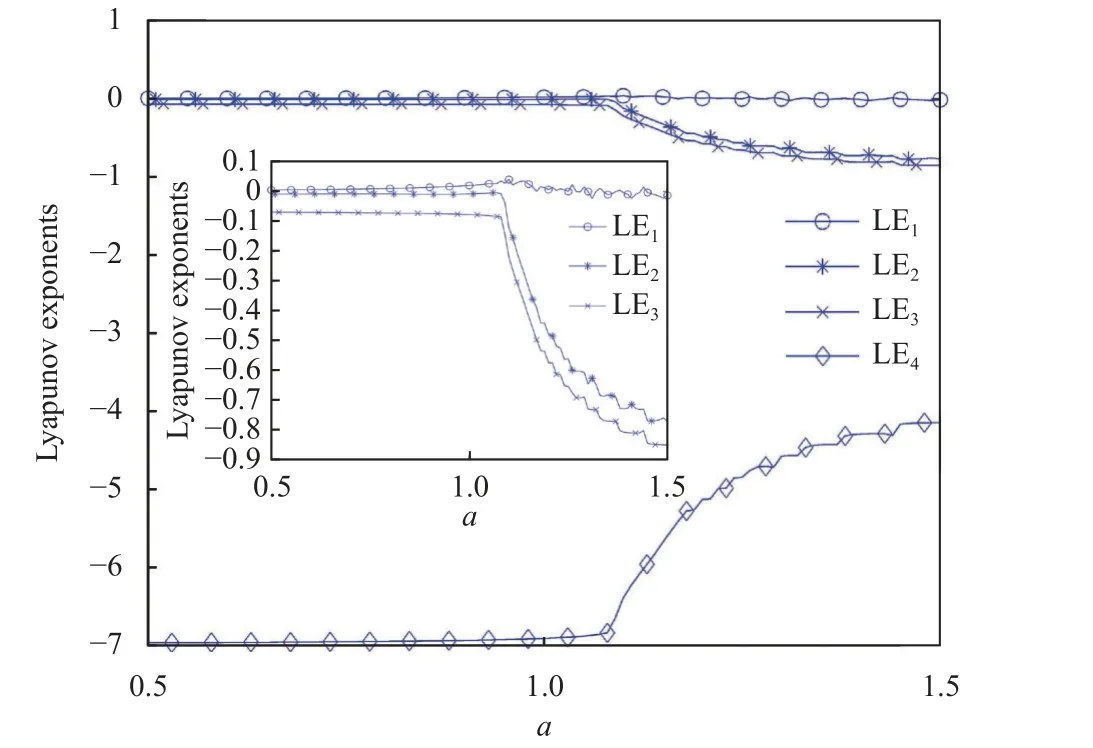
圖6 Lyapunov 指數隨a 值變化的曲線圖

如圖7 所示，b取[0.05, 0.12]，步長為0.001，b的取值持續對Lyapunov 指數造成影響，證明憶阻器的衰減項對系統的影響較大，但不論b取何值，LE1始終大于零，其他Lyapunov 指數小于零。

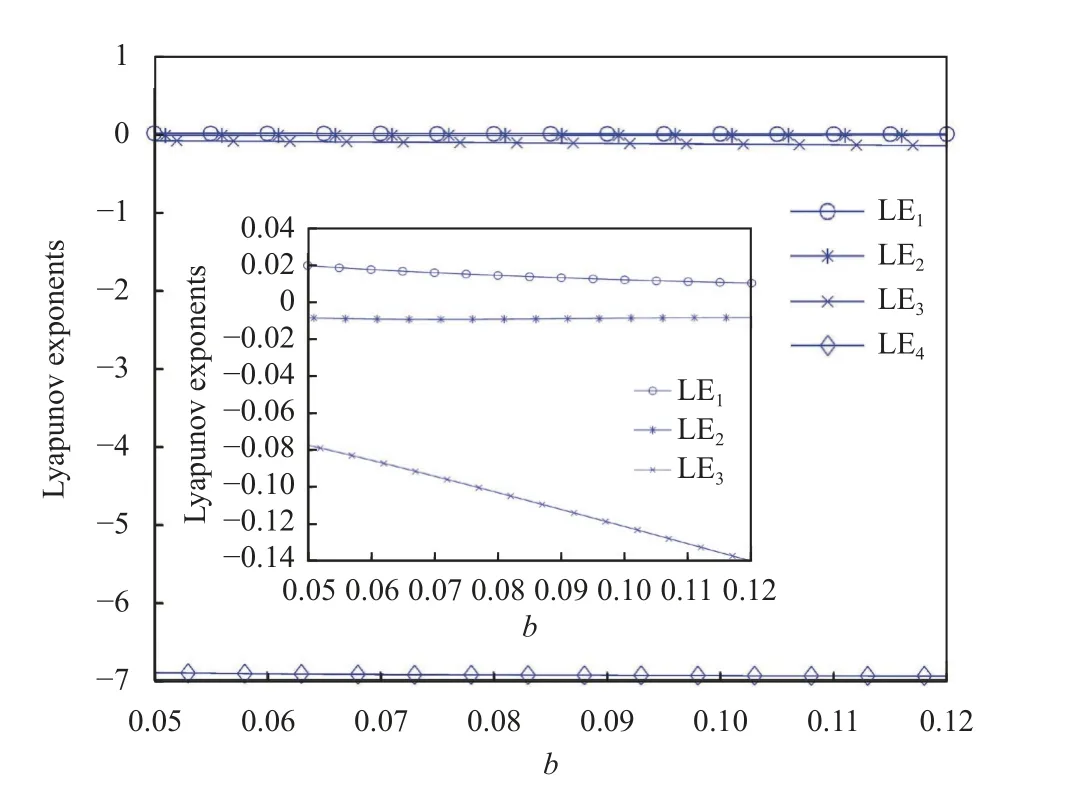
圖7 Lyapunov 指數隨b 值變化的曲線圖

3.2 連接權值矩陣的影響

神經元間的連接權值矩陣對系統有較明顯的影響，實驗中搜索出另一組連接權值矩陣Wn如下：

如圖8 所示，系統呈現出圖4 類似的單渦卷吸引子相軌圖，且只有LE1=0.008 9，大于零，其他Lyapunov 指數均小于零。

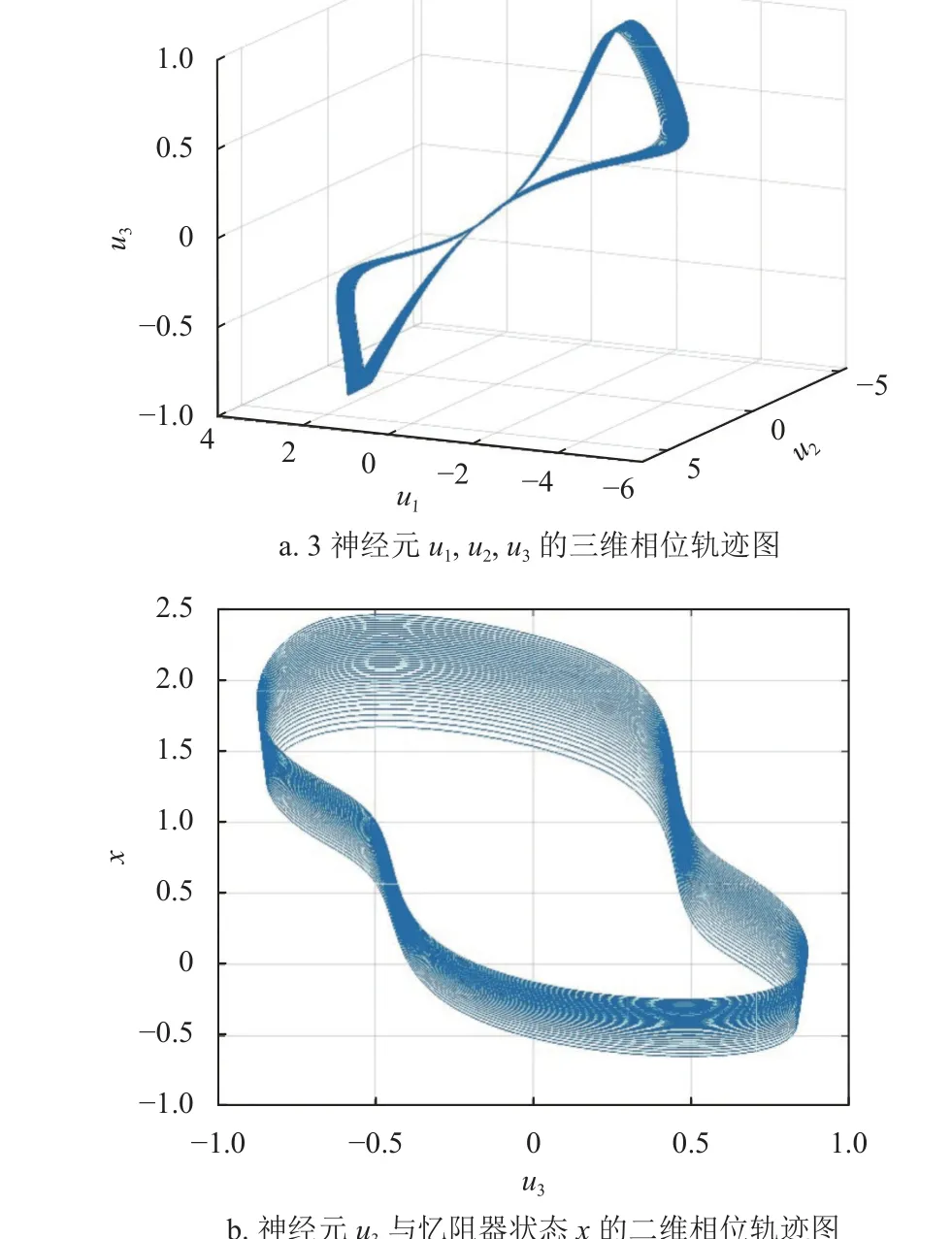
圖8 系統的相位軌跡圖(W 取Wn)

3.3 與其他Hopfield 神經網絡對比

如表1 所示，Hopfield 神經網絡的相軌圖主要集中表現為單、雙渦卷吸引子，Lyapunov 指數一般只有一個為正。文獻[21]是最早將混沌引入HNN網絡的，但10 神經元模型的動力學行為并不顯著，而后續的改進模型性能都有所提升。

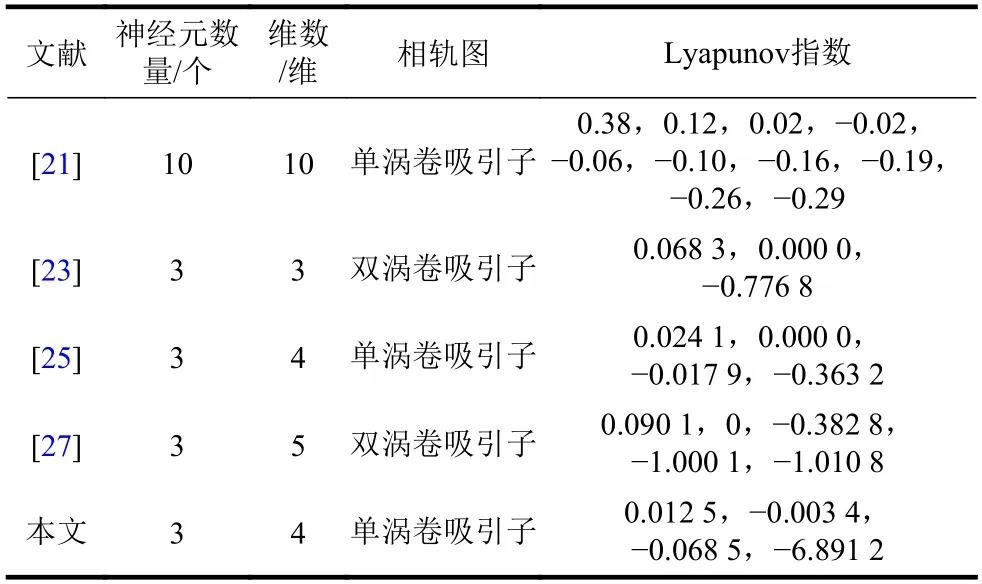
表1 本網絡與其他HNN 模型的動力學特性對比

4 結 束 語

本文通過對具有負阻態的憶阻器模型進行數學分析以及I-V特性仿真測試，進一步明確了憶阻器的器件特性，同時基于該憶阻器模型構建了新的Hopfield 神經網絡，并對網絡的動力學行為進行了分析與討論。實驗結果表明，提出的Hopfield 神經網絡模型具有豐富且復雜的動力學行為，并存在一定的混沌現象。同時，討論了在不同的憶阻器參數以及連接權值矩陣條件下，網絡的動態演化進程以及Lyapunov 指數的變化情況，并與同類型網絡進行了對比，結果進一步表明該模型的有效性，為后續在模式識別、數據處理以及圖像加密方面的應用提供了研究思路。