分布式穿墻成像雷達空間配準方法

李虎泉，郭世盛，陳家輝，崔國龍，孔令講

(電子科技大學信息與通信工程學院 成都 611731)

穿墻成像雷達通過發射低頻電磁波穿透建筑墻體，實現對室內人體目標的實時成像定位[1-2]，在城市作戰、反恐維穩、災難救援等領域具有重要的應用前景[3-4]。由于室內環境的復雜性，單雷達穿墻探測存在遮蔽盲區、定位精度低、虛假目標干擾等問題。分布式穿墻成像雷達利用多個雷達節點在多個視角對室內目標進行協同探測，可以有效彌補單雷達探測的不足[5-6]，已成為當前國內外研究熱點。

分布式穿墻成像雷達各個節點的位置誤差會導致目標定位跟蹤結果出現偏差，從而影響多節點信息融合，因此，雷達節點的空間配準是分布式穿墻成像雷達需要解決的首要問題。現有雷達網絡可基于衛星信號或輔助定位設備獲取各個雷達節點的位置，然而城市環境中存在大量建筑物遮擋，衛星信號獲取困難、定位精度差；而輔助定位設備會增加系統復雜度，且在城市作戰中部署不便。因此，現有研究主要集中于無需輔助定位的雷達節點空間配準算法。

計算機視覺與遙感領域采用多個傳感器對同一個物體成像時，可在多傳感器成像結果中尋找成像物體的共同特征，進而推算出各個傳感器的位置。文獻[7] 提出了基于互信息的多極化穿墻成像雷達圖像配準算法，根據區域特征實現圖像配準。文獻[8] 提出了基于改進尺度不變特征變換的遙感圖像配準算法。然而，上述算法只適用于高分辨率圖像，而穿墻成像雷達分辨率有限，不同節點成像結果中目標不具備形狀、紋理等顯著的共同特征。

當探測場景中存在多個目標時，各個雷達節點成像結果中目標的空間分布存在相似性，由此可根據目標檢測結果中量測點的相對位置關系推算節點位置，從而將雷達節點配準問題轉化為點集匹配問題。基于上述思路，文獻[9] 提出了一種基于圖匹配的穿墻成像雷達節點配準算法，基于雷達量測點構建完全圖模型，并求解多節點量測的關聯關系，最后計算出坐標變換參數，實現雷達節點配準。該算法直接求解目標關聯關系，在量測誤差較小時可以取得較為準確的配準結果。然而，該算法需要已知兩個節點共同觀測到的目標個數，因此無法處理漏檢與虛警情況。此外，該算法未考慮量測誤差影響，量測誤差較大時配準精度降低。針對存在量測誤差條件下的點集配準問題，文獻[10] 提出了基于高斯混合模型的配準算法，采用高斯混合模型建模整個量測點集的位置分布，并通過點集距離最小化準則計算坐標變換參數，從而實現點集配準。

針對分布式穿墻成像雷達空間配準問題，本文提出了一種基于高斯混合模型的節點配準方法。首先采用旋轉平移坐標變換表征各個雷達節點的相對位置關系，并將各個雷達節點獲取到的量測點集建模為高斯混合模型；然后將雷達節點配準問題轉化為求解最優坐標變換參數的優化問題，并采用L2距離衡量各個節點量測點集與參考節點量測點集之間的距離；最后，采用粒子群優化算法求解上述配準問題，得到雷達節點坐標變換參數，從而確定各個雷達節點相對位置，最終實現雷達節點空間配準。

1 系統模型

分布式穿墻成像雷達由多個雷達節點與融合中心組成，多個雷達節點部署于多個視角，對建筑環境中多個人體目標進行協同探測，典型工作場景如圖1 所示。

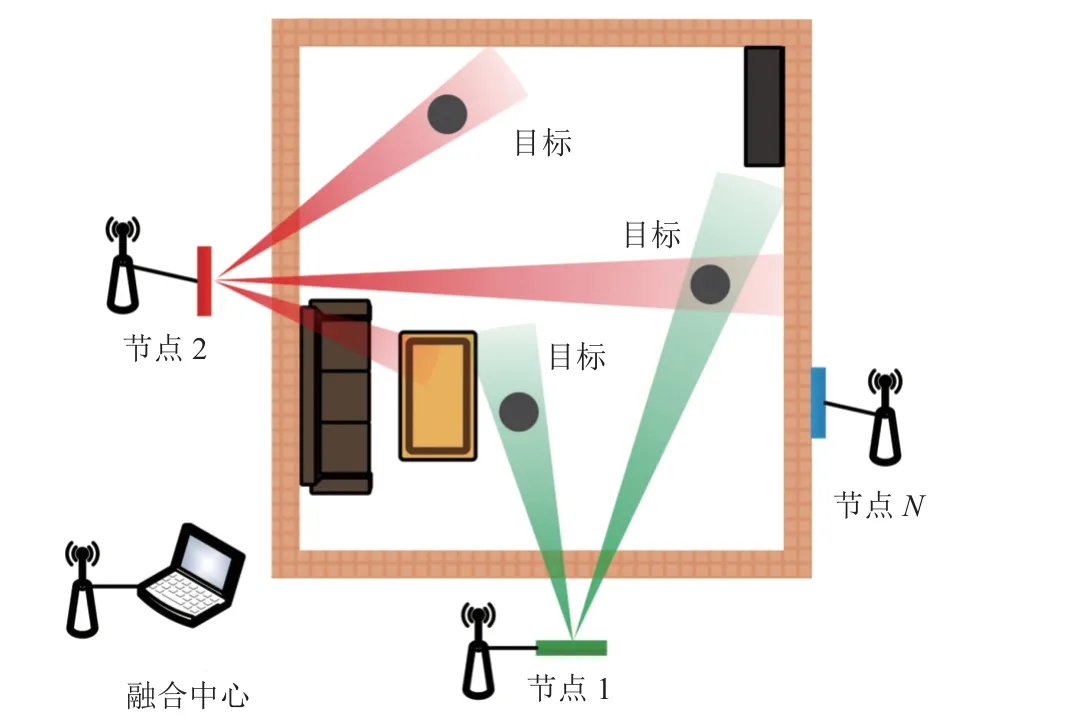
圖1 分布式穿墻成像雷達目標探測示意圖

假設雷達節點配備M個發射單元與N個接收單元，M個發射陣元依次發射超寬帶脈沖信號s(t)，發射信號經過目標與環境反射后被N個接收陣元接收。當節點i的 陣元Tm發射信號時，接收陣元Rn接收到的回波信號可表示為：

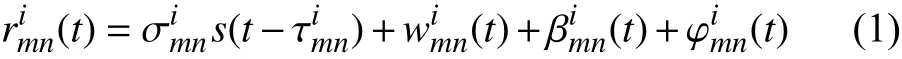
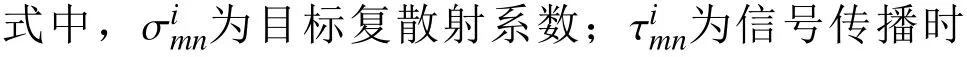
由于人體目標散射截面積遠遠小于墻體等建筑結構，同時電磁波在墻體內部的衰減導致信號穿透墻體后能量大幅損失，式(1)中靜止強散射體回波wimn(t)強度遠大于目標回波。考慮到不同探測周期中靜止強散射體回波基本保持不變，而人體目標存在輕微晃動或大幅運動，本文采用脈沖對消器[11]抑制墻體回波，經過對消后回波表示為rˉmin(t)。

反投影成像算法[12]因其實現簡單、無需探測場景先驗信息等優點廣泛應用于穿墻透視成像中。反投影成像算法的基本思想為將MN個通道回波分別映射到二維成像空間，并相干疊加得到二維雷達圖像。將探測區域離散為Q個像素點，根據反投影成像算法，節點i成像結果中像素點xq的像素值計算如下：

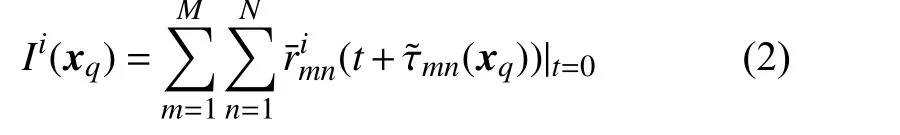
式中，τ ?mn(xq)為計算時延。本文采用固定時延補償法[13]補償電磁波穿透墻體引起的時延，并基于能量相干因子算法[14]抑制旁瓣。

2 基于高斯混合模型的空間配準算法

2.1 多節點量測模型

分布式穿墻成像雷達系統中，所有雷達節點基于自身坐標系進行目標定位跟蹤。假設每個雷達節點陣列中心位于自身坐標系的原點處，且其他雷達節點位置與角度未知。為了融合多節點信息，需要建立統一的坐標系。

本文將其中一個雷達節點作為參考節點，將其自身坐標系作為參考坐標系，其他節點坐標系可以表示為參考坐標系的旋轉平移坐標變換，如圖2 所示，進而通過求解各個節點的坐標變換參數實現節點配準。

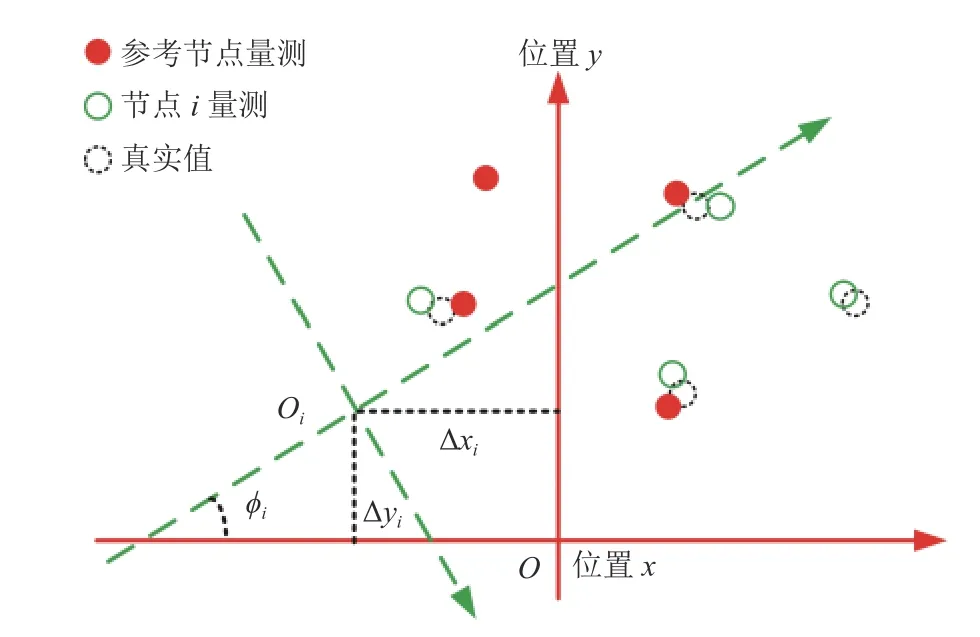
圖2 雷達節點配準示意圖

式中， φi為旋轉角度。

由于雷達節點分辨率的限制，目標圖像方位向擴展與目標距離成正比，因此不同雷達節點成像結果中目標幅度與形狀均不相同[15]，因此需要根據成像結果估計目標位置與量測誤差。二值圖像Ibin(x,y)的 (i+j)階矩定義為[16]：

2.2 雷達節點配準

式中， ?為Kronecker 積； 1mi×1表 示mi行1 列的全1 矩陣。

在節點i自身坐標系下，目標p位 置xip的概率密度函數可表示為：

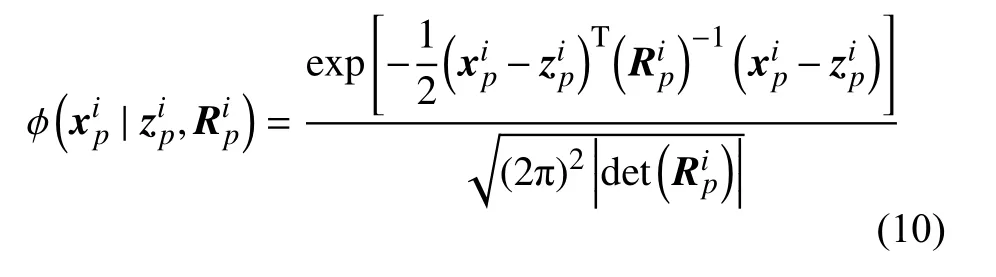
式中， d et(·)為 矩陣行列式。節點i觀測到的所有目標位置的概率密度函數可表示為mi個高斯模型的疊加，得到高斯混合模型：

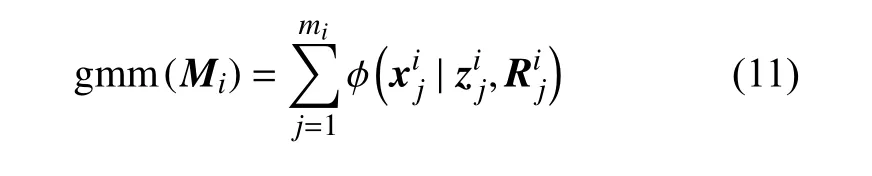
式中，zij為 第j個量測值；Rj為對應量測誤差協方差矩陣。

式(12)中L2距離共包含3 項，第一項與坐標系變換無關；對于剛性變換(對稱、平移與旋轉變換)，第二項為固定值。因此L2距離可化簡為兩個高斯混合模型乘積的積分：

在雷達節點配準問題中，變換參數 θi的估計精度主要取決于點集M0與Mi中量測點的數量、量測誤差大小、量測點的空間分布與優化算法。當量測點過少時，配準問題可能產生多解。為了在完全無先驗信息的條件下實現雷達節點配準，需要點集M0與Mi中至少存在3 個源于共同觀測目標的量測點。

當探測場景中目標數量不足3 個時，可采用多周期量測點進行配準，此時式(8)中f(·)可表示為：

本文采用粒子群優化(particle swarm optimization,PSO)算法[17]求解式(8)中的優化問題，流程如下。

1) 隨機初始化J個三維粒子，3 個維度分別對應 θi的3 個參數。每個粒子具有位置與速度兩個屬

6) 若目標函數值fn小 于預設閾值或達到最大迭代次數，將全局最優位置作為優化結果，即θi=Pn；反之，返回步驟2)。

3 仿真結果

為了驗證基于高斯混合模型的雷達節點配準算法的有效性，本文采用數值計算軟件模擬分布式穿墻成像雷達多目標探測。仿真中采用兩個雷達節點探測兩個運動目標，全局坐標系下，仿真場景如圖3 所示。

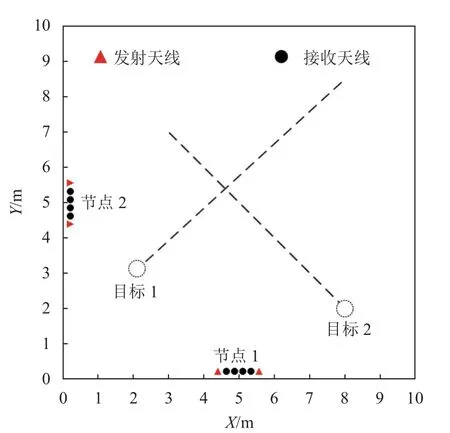
圖3 仿真場景

兩個節點均采用兩發四收天線陣列，全局坐標系下節點1 陣列中心設為(5 m, 0 m)，發射天線坐標分別為(4.85 m，0 m)與(5.15 m，0 m)，接收天線位置分別為(4.887 5 m，0 m)、(4.962 5 m，0 m)、(5.037 5 m，0 m)與(5.112 5 m，0 m)，陣列角度0°；節點2 陣列中心設為(0 m, 5 m)，陣列布局與節點1 相同，陣列角度90°。兩個雷達節點均發射步進頻連續波信號，頻率范圍為1.6～2.2 GHz。為簡化問題分析，仿真中沒有加入墻體。兩個目標均作勻速直線運動，目標1 起點為(2 m, 3 m)，終點為(8 m, 8 m)；目標2 起點為(8 m, 2 m)，終點為(3 m, 7 m)。兩個目標同時開始運動，運動過程共持續8 個周期。

產生多周期回波信號后，采用逆傅立葉變換算法進行脈沖壓縮。脈沖壓縮結果中加入了高斯白噪聲，以最大值作為信號強度，信噪比設置為8 dB。部分周期成像結果如圖4 所示。

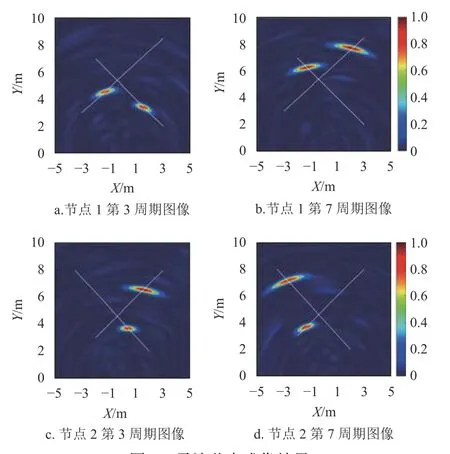
圖4 雷達節點成像結果

每周期成像結果經過閾值檢測后得到目標區域，進而根據式(6)與式(7)分別計算目標形心與量測誤差協方差矩陣，得到量測點集。

雷達節點配準結果如圖5 所示。圖5a 為配準前兩個節點在自身坐標系下獲取到的量測，實心點為節點1 量測，空心點為節點2 量測；圖5b 為配準結果。由于目標圖像存在擴展與輕微形變，目標圖像形心不能完全反映目標準確位置，因此節點2 量測點集經過坐標變換后無法與節點1 量測點集完全重合。

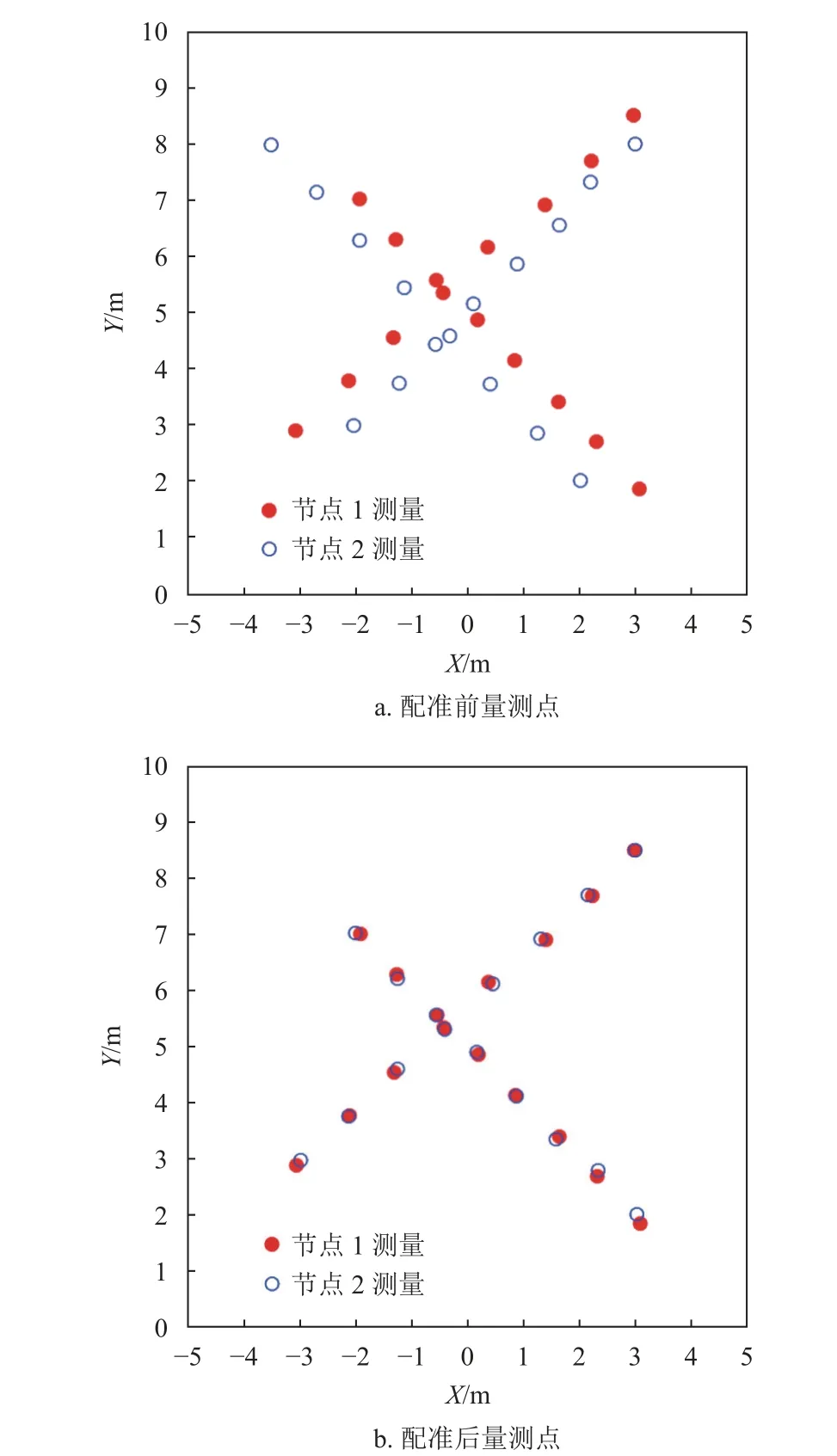
圖5 雷達節點配準仿真結果

為了進一步驗證雷達配準算法的準確性與魯棒性，分別采用500 次蒙特卡洛仿真測試無漏檢無虛警、有漏檢無虛警、有漏檢有虛警條件下的配準算法性能。在有漏檢條件下，每個目標檢測概率設置為80%；在有虛警條件下，每個周期有10%的概率在探測區域中隨機位置出現假目標。此外，為了測試粒子群算法中粒子數量對參數估計精度的影響，分別計算了粒子數J=100與J=500時，3 種條件下節點2 的變換參數，并計算變換參數與真實值的誤差，6 種情況下誤差累積分布曲線如圖6 所示。

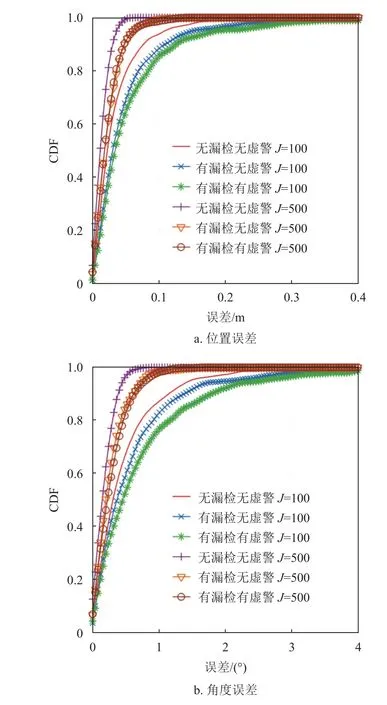
圖6 不同條件下誤差累積分布曲線

由結果可知，粒子數為500 時，3 種條件下位置誤差小于0.05 m 且角度誤差小于1°的概率大于90%，粒子數減少至100 時，配準精度下降。當粒子數相同時，無漏檢無虛警條件下配準誤差明顯小于有漏檢無虛警及有漏檢有虛警條件。對于雷達配準問題，漏檢與虛警均會導致另一個節點獲取到的量測點集中沒有量測點與之對應，從而增大配準難度，導致配準誤差增大。

在無漏檢無虛警條件下，采用500 次蒙特卡洛仿真測試了文獻[9] 中提出的基于圖模型的雷達節點配準算法性能，并與本文算法進行對比，得到兩種算法誤差累積分布曲線如圖7 所示。

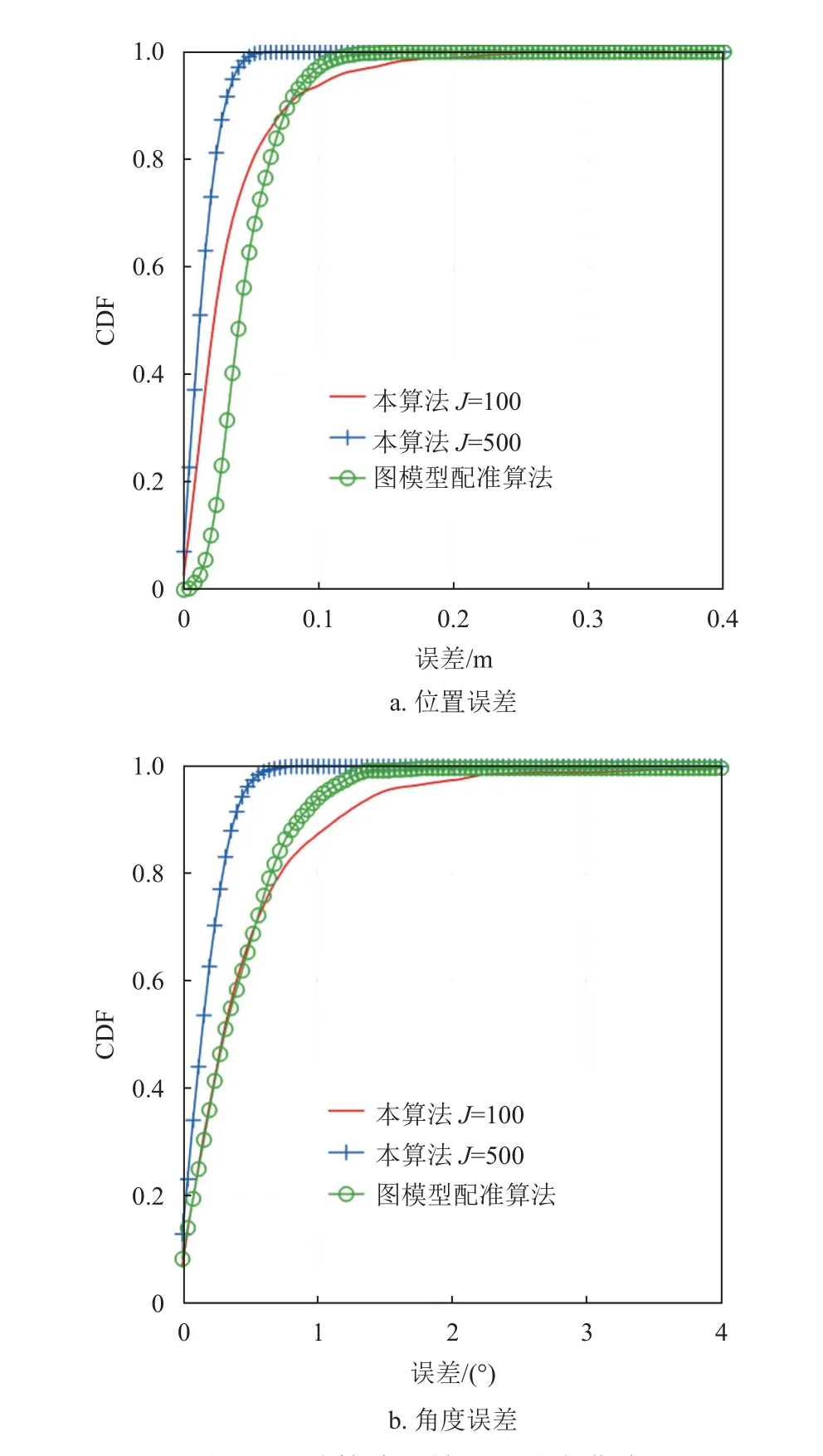
圖7 兩種算法誤差累積分布曲線

基于圖模型的雷達節點配準算法利用多節點成像結果中多目標空間分布結構的相似性，構建完全圖模型求解兩個節點探測結果中對應目標的關聯關系，最后計算出坐標變換參數。然而，該算法需要已知兩個節點共同觀測到的目標數量，因此無法處理漏檢與虛警情況。此外，該算法未考慮量測誤差的影響，量測誤差較大時配準精度降低。粒子數為500 時，本算法配準性能優于基于圖模型的雷達節點配準算法；當粒子數降至100 時，本算法性能略低于圖模型算法。由于本算法無需已知兩個節點共同觀測到的目標個數，且配準過程中考慮到了不同量測點量測誤差的差異，在實際應用中具有更強的魯棒性。

4 實測結果

為了驗證實際應用中本文提出的雷達節點配準算法的有效性，采用兩個兩發四收穿墻成像雷達節點協同探測房間內兩個運動人體目標，雷達節點參數與仿真相同。實測場景如圖8a 所示，房間尺寸約為8 m×8 m，墻體材質為實心磚，厚度約為0.22 m。以墻角為原點，建立全局坐標系如圖8b所示。在全局坐標系中，節點1 陣列中心坐標為(4 m, 0 m)，節點2 陣列中心坐標為(0 m, 5 m)。兩個目標均做勻速直線運動，在全局坐標系下，目標1 起點為(2.5 m, 4.5 m)，終點為(5.0 m, 1.5 m)；目標2 起點為(6.0 m, 5.5 m)，終點為(4.5 m, 3.0 m)。

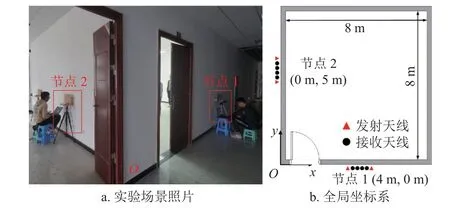
圖8 實驗場景

目標探測共持續18 個周期，雷達節點信號處理方法與仿真相同。兩個節點成像運算均在自身坐標系下進行，成像范圍為10 m×10 m，像素點尺寸設置為0.03 m，部分周期成像結果如圖9 所示。

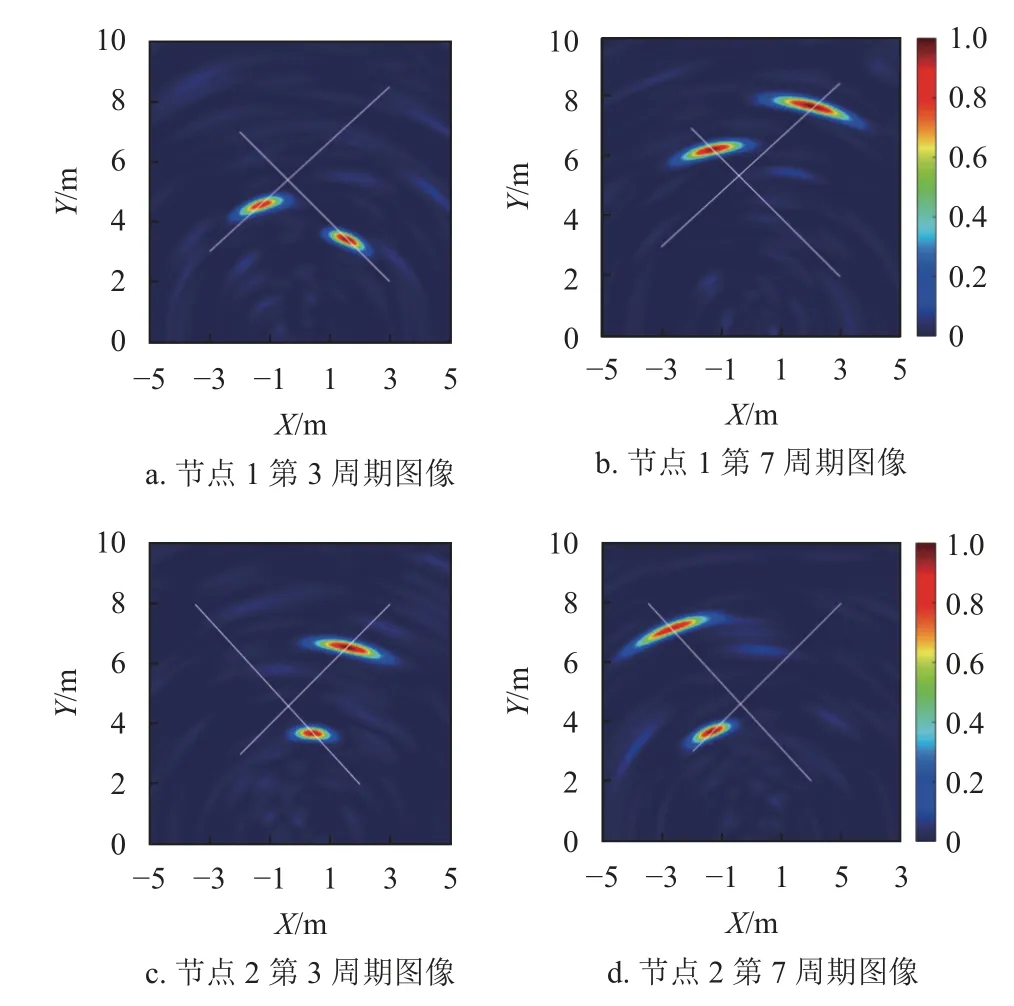
圖9 運動目標成像結果

由于墻體材質的非均勻性，目標圖像出現擴展與形變，且不同周期目標圖像形狀差異明顯，甚至部分周期出現圖像分裂。此時目標圖像形心明顯偏離實際位置，雷達獲取到的量測點存在較大量測誤差。同時由于運動過程中目標姿態實時變化，不同周期目標相對強度存在顯著差異，部分周期出現圖像缺失。此外，兩個節點成像結果中墻體位置附近均出現遮蔽鬼影，帶來了大量虛假量測。

經過目標檢測后，兩個節點獲取到的量測點如圖10a 所示。進而采用本文提出的基于高斯混合模型的雷達節點配準算法計算節點2 的旋轉平移變換參數，粒子群優化器參數與仿真相同。雷達節點配準結果如圖10b 所示。

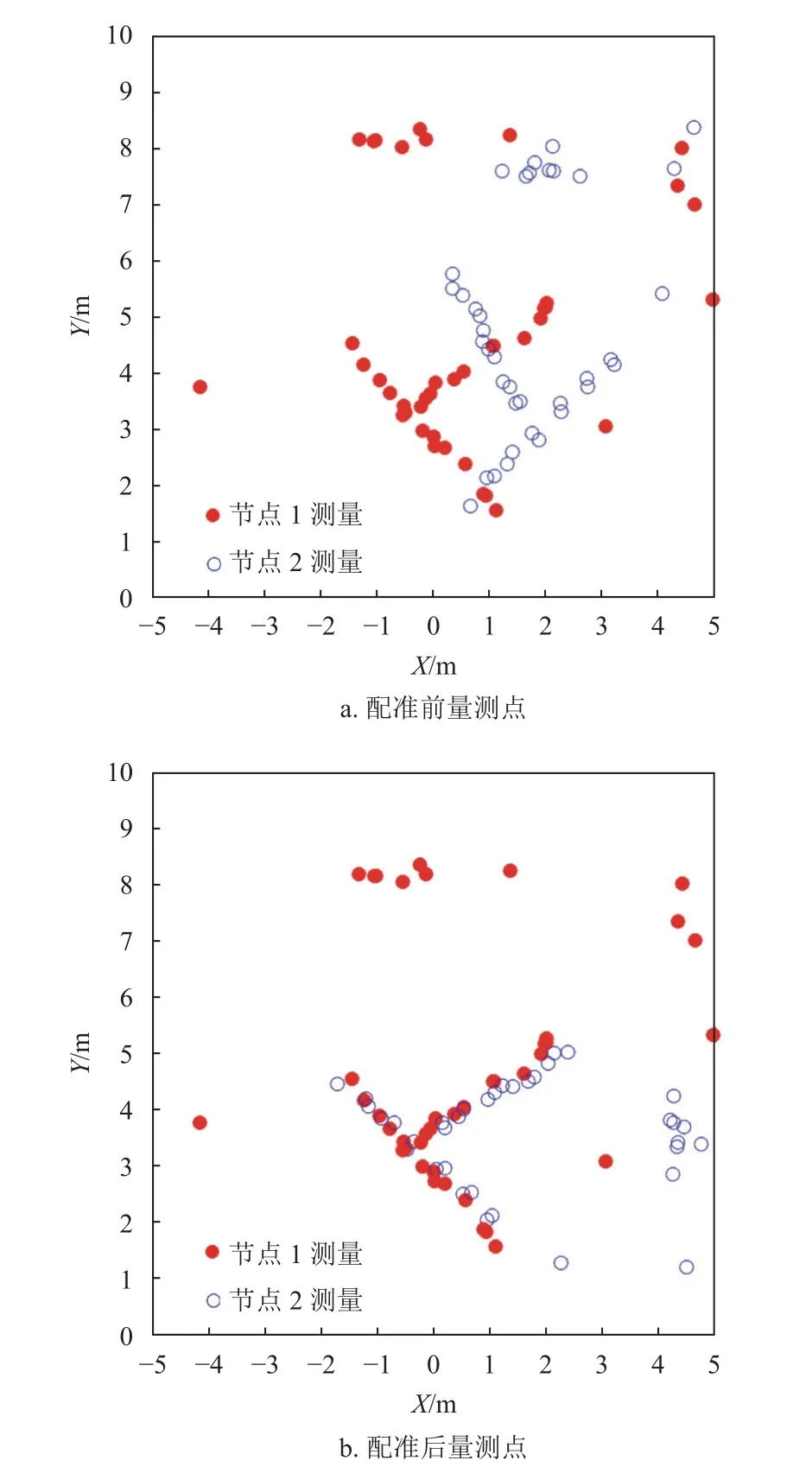
圖10 雷達節點配準結果

由于本實驗中目標圖像形變與擴展與仿真相比更為嚴重，雷達節點量測誤差更大，經過配準后兩個節點的量測點集仍然存在一定偏差。與雷達節點真實位置相比，20 次實驗中本算法輸出配準結果平均位置誤差為0.19 m，平均角度誤差為3.15°。此外，由于該實驗中漏檢與虛警問題嚴重，無法獲取兩個雷達節點共同觀測到的目標數量，文獻[9]中基于圖模型的雷達節點配準算法無法使用。

5 結 束 語

本文提出了一種基于高斯混合模型的分布式穿墻成像雷達空間配準方法，將雷達節點獲取的量測點集建模為高斯混合模型，并采用L2距離計算各個節點量測點集與參考節點量測點集之間的距離，最終基于粒子群優化算法求解出旋轉平移變換參數。該算法無需額外輔助定位設備，僅根據各個節點探測結果實現雷達節點空間配準。仿真與實測結果表明，與現有算法相比，該方法無需求解多節點多目標之間的關聯問題，且對于量測誤差具有較好的魯棒性。