基于變分量子虛時演化和UCC Ansatz 的基態求解器

儲貽達，徐 維，周彥樺，張學鋒

(重慶大學物理學院 重慶 沙坪壩區 401331)

量子計算能降低算法的時間復雜度，有望大幅提升算力。然而，就目前而言，大量量子比特糾纏在技術上仍面臨巨大挑戰。因此，在相當長的一段時間內，量子計算機的下一步發展可能更傾向于有一定噪聲的中型量子計算機，其對應的算法為嘈雜中型量子算法(noisy medium-scaled quantum algorithm, NISQ)[1-2]。其量子比特數有限，沒有可靠的糾錯方案，因此存在一定的噪聲，在這種設備上，某些經典量子混合算法可能具有巨大優勢。經典量子混合算法是將算法的一部分運行在經典計算機上，其他部分運行在量子計算機上，要在NISQ 上具有優勢就要求算法不需要太多的量子比特，且能容忍一定噪聲。變分量子本征求解器(variational quantum eigensolver, VQE)正是這樣一類算法[3]。

VQE 在量子計算機編碼波函數擬設 |ψ〉，再用經典計算機優化 |ψ〉中的變分參數，從而通過降低哈密頓量H的期望達到計算最小本征值E0的目的[4]。當利用變分原理計算分子或材料的基態時，在經典計算機上會遇到多體波函數隨系統大小指數增大導致無法精確模擬的問題。但是，由于VQE 對于系統基態的擬設是在量子計算機上完成的，其時間復雜度僅是多項式級的。并且，作為變分算法，其對于噪聲具有一定的抵抗能力。當量子計算機硬件進一步提高可糾纏量子比特數量，或減少噪聲后，VQE 算法有望使NISQ 呈現出更強的算力，完成量子計算機發展的階段性目標。VQE算法已經通過離子阱量子計算機實現了對水的基態能的計算[5]，激發態VQE 則用于研究多體局域化[6]，多態收縮VQE 則用于研究電子躍遷過程[7]。

此外，VQE 算法在NISQ 上有望解決量子化學中一些較大分子的基態問題，而傳統算法由于原子數過多，希爾伯特空間太大，無法在經典計算機上精確求解。但隨著分子體系的增大，VQE 方法所需的量子線路的復雜度和變分參數的數目也會隨之增大，導致VQE 算法的收斂速度及有效性受到影響。目前有一些開源平臺上集成了VQE，可以直接在它們的函數庫上完成VQE 的模擬。本文在mindquantum 平臺[8]上基于VQE 嘗試使用變分量子虛時演化算法來更新參數，并結合優化UCC(unitary couple cluster)擬設來設計量子線路，構造一種有效快速的量子基態能求解器。

1 表象選擇

為了方便表示哈密頓量，需要選擇一個合適的表象，因為在合適的表象下處理所需要考慮的希爾伯特空間的維度會大大降低，從而大幅降低計算所需的資源消耗。通常采取的表象有：STO、GTO、STO-nG 等[9]。對于小分子而言，STO-3G 是最廣泛使用的表象。雖然STO-3G 是最普適的一組基矢，但是針對特定的分子而言，肯定有著比STO-3G 更加合適的表象。為了得到這個表象，本文對哈密頓量進行預處理。

首 先 使 用 如 CCSD(coupled cluster single and double excitation)[10]之類的經典方法得到體系的單電子約化密度矩陣 ρ ， ρ 是 一個n×n的 矩陣，n是分子軌道的數目。為了消減活躍空間(active space)的大小，對單電子約化密度矩陣進行對角化：

這樣就完成了從STO-3G 表象到新的基底表象的變換。將新的基底稱之為自然分子軌道(natural molecular orbitals)[11]，V是基底間的變換矩陣，D是在自然分子軌道下的單電子約化密度矩陣。當然，借助幺正變換V分子哈密頓量也需要在自然分子軌道表象中寫出。對于對角矩陣D， 其對角元Dii稱之 為 自 然 軌 道 占 據 數(natural orbital occupation numbers)，它的大小就表示該軌道下的平均占據數。如果對角元大于某個閾值χmax，則可以視為該自然軌道必然被占據。反之如果對角元小于某個閾值 χmin，則可以視為該自然軌道零占據。所以，在接下來的量子基態能變分求解中，本文只保留Dii∈[χmin,χmax]所對應的軌道。這樣一來，活躍空間的維度便降低了。這使得在后續的變分算法中，不僅簡化了所需的哈密頓量的項數，而且變分參數和量子線路的比特數也能夠得到有效的減少。

2 UCC 擬設

2.1 基本原理

UCC 來自經典的couple cluster ansatz，最早出現于核物理的計算，后廣泛應用于量子化學的計算[12]，它是一種對于多體波函數形式的假設，具體表示為：

在這個擬設下，通過梯度下降之類的方法優化參數c，可以得到高精度的結果。

2.2 量子線路中的實現

量子邏輯門是幺正的，因此，實現的 eT也是幺正的，所以：

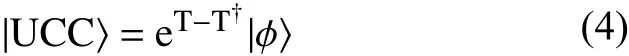
即unitary couple cluster ansatz。從算符上來說，它只包含費米子產生湮滅算符。

在量子計算機上編碼費米子系統可以采用Jordan-Wigner 變換[13-14]，將產生湮滅算符表示如下：

式中， θn為 一個實數；an∈{x,y,z}標記不同的泡利矩陣；bn為互不相同的各個軌道。其中不同項之間，同軌道的算符必然同為 σz或 都不為 σz，因此它們之間的對易關系只取決于σxσy。計算可得到上式中任意泡利算符鏈的對易[12]：

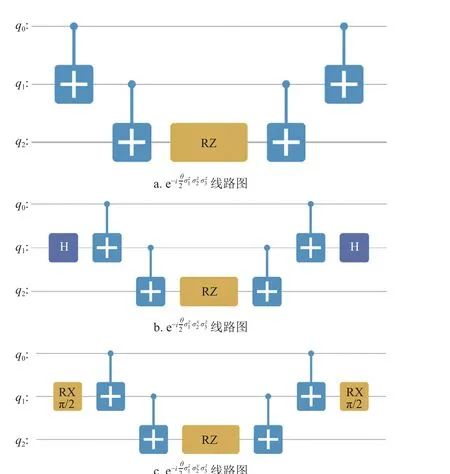
圖1 量子線路圖

2.3 優化

在文獻[15]中，T只保留兩體項和四體項，根據參考態，將軌道分為占據道和虛軌道的算法稱為UCCSD(unitary couple clustersingle and double)，不 分 軌 道 的 稱 為UCCGSD(unitary couple cluster general single and double)。UCCSD 的 線 路 深 度為 (N?η)2η ，而UCCGSD 的 線 路 深 度 為N3， η是電子數，N是軌道數，往往是 η的幾倍，因此UCCSD 需優化的參數大量減少，線路深度也大大減少。

3 變分虛時演化算法

除了前面所提到的基于UCC 的ansatz 線路的構建，還需要一個有效的算法來完成變分過程以得到分子的基態。在傳統的VQE 算法中常常使用一些梯度算法達到這一目的，而本文運用虛時演化的方法更好地完成了變分過程。

虛時演化方法是研究量子體系的強大工具，除了可以視為配分函數研究系統的熱力學統計性質外，還可以用來計算多體系統Hamiltonian 的基態問題。如對于一個分子體系，如果給定一個任意初始態 |ψ〉，那么其虛時演化態可以定義為：

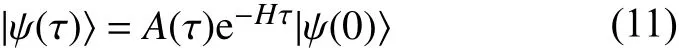
VITE 算法設想在量子線路中，運用含參的量子 態 |?(θ(τ))〉模 擬 得 到 演 化 態，其 中θ(τ)={θ1(τ),θ2(τ),···,θN(τ)}。而這樣一來就可以運用量子門在量子線路上制備這一含參態。具體做法是將一系列的量子門

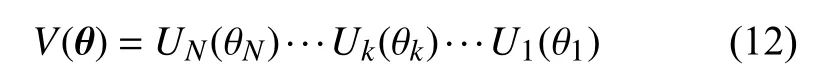
作用在初始態零態 |0ˉ〉 上 ，即 |?(θ)〉=V(θ)|0ˉ〉。這 里的V(θ)也就是ansatz 線路。如果對含參的演化態運用麥克阿蘭變分原理(McLachlan's variational principle)[17-18]：

如 果 將 總的演化時間 τtotal分 成N份，即τtotal=Nδτ。 將上述操作重復N次，直至最終的 |?(τ)〉收斂到基態，進而得到基態能EGround=〈ψ(τ)|H?|ψ(τ)〉。

總之，VITE 算法運用參數化的ansatz 線路來得到含參的演化態，借助麥克阿蘭變分原理將虛時演化的過程轉化為一個在量子線路上實現的演化過程，并最終給出了ansatz 線路的參數更新所需滿足的要求。

4 算法結果

本文運用上述算法對LiH 分子基態能進行求解。首先選取鍵長為4.0 埃的LiH 分子，借助openfermionpyscf 函數庫[19]得到其在STO-3G 基矢下的哈密頓量H以及通過FCI 方法得到的基態能的精確解EFCI。按照第二章所說的方法，分析單電子約化密度矩陣ρ，設置自然軌道占據數的最小閾值χmin=10?4和最大閾值 χmax=1.999 5。經過預處理后，將原有哈密頓量從6 個分子軌道簡化為只有2 個分子軌道。借助Mindquantum 函數庫[8]構建一個UCCSD 的量子線路作用于活躍空間占據的參考態上。

經過分子哈密頓量簡化后得到的量子線路深度大大降低，并且所需要變分的參數和量子比特數也大幅下降，如表1 所示。接下來運用梯度下降算法來完成變分求解基態。圖2 給出了每一步變分迭代的能量和EFCI能量的比值。可以看到，雖然運用簡化后的哈密頓量得到的UCCSD ansatz 的線路來完成基態能變分求解，但與簡化前的結果相比，并沒有在最終的能量上損失太多精度。此外，對于簡化前的變分求解，在合適的區間內學習率的大小與算法的收斂速度成正比。但是過大的學習率會給參數學習過程帶來波動，這是因為梯度下降算法會隨之增大而失去方向性，使得參數的優化朝著錯誤的方向進行。而簡化后得到的UCCSD 線路所需優化的參數數目大幅下降，使得變分算法的參數空間更簡單，因此可以在梯度下降的時候選取更大的學習率。這樣不僅使得每一步迭代所需的計算時間減少，且迭代收斂更快。但由于梯度算法的限制，本文發現更大的學習率仍然會導致波動。以上的結果 驗證 了 在選 取 合適 的 截斷 閾 值 χmin和 χmax情況下，可使用更簡單的量子線路更快完成基態變分求解。

表1 簡化哈密頓量前后的ansatz 線路復雜度對比

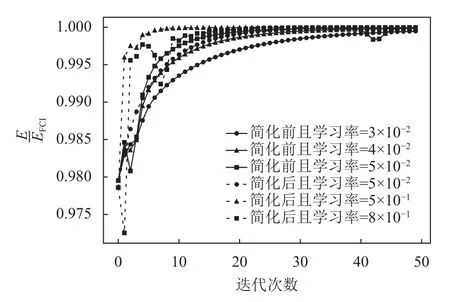
圖2 簡化哈密頓量前后的收斂結果

除此之外，針對上述的LiH 分子，本文還基于Mindquantum 函數庫實現變分虛實演化算法結合簡化后的UCC ansatz 線路來完成分子基態的求解。圖3 給出了VITE 算法在不同的 δτ的情況下，每一步變分迭代的能量與EFCI能量的比值以及梯度下降算法所得到的比值。結果顯示，VITE 算法不僅可以有效計算得到分子的基態能，還可以比梯度下降算法更快收斂到基態。由于VITE 基于虛時演化的原理，所以基于VITE 算法得到的每一步參數的更新具有明確的方向性，不再受參數空間的梯度分布的影響。這使得即使用更大的更新步長即 δτ來減少收斂所需的更新次數，也不會導致收斂過程產生波動。

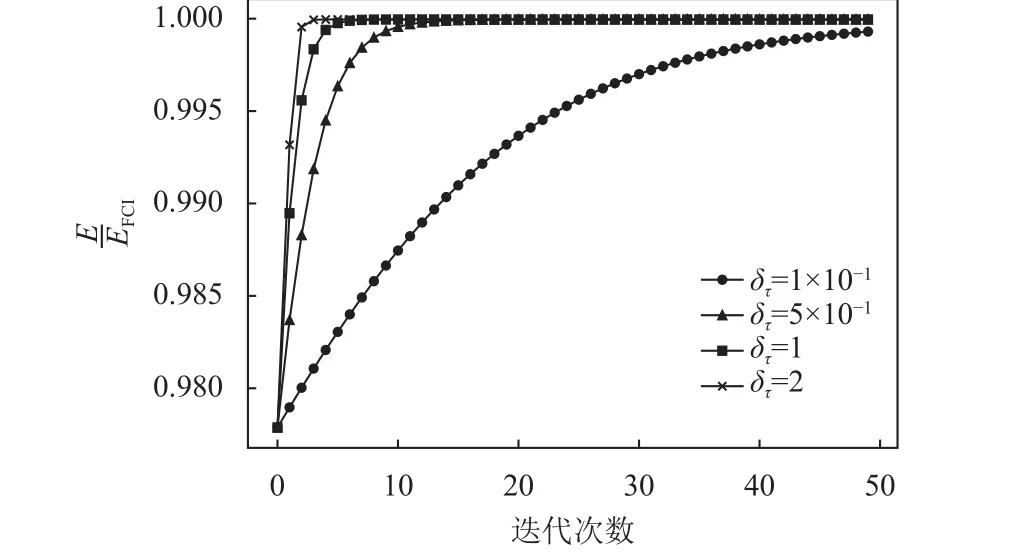
圖3 運用VITE 算法更新參數的收斂結果

5 結 束 語

本文針對量子化學中的分子體系基態求解問題，提出了一種基于VQE，將單電子約化密度矩陣分析、變分虛時演化和UCC ansatz 量子線路相結合的變分量子基態求解器。該求解器通過分析分子體系的活躍空間簡化了體系的哈密頓量，進而優化了UCC ansatz 線路的構造。并且在傳統VQE 算法基礎上引入變分虛時演化算法，使其可以更快地收斂得到基態。該變分基態求解器的算法框架具有普適性，可以將其擴展到更多的量子多體體系的基態求解問題上，進而探究其中的物理特性。