基于頻率的索力測量方法研究

趙震寅

(浙江理工大學建筑工程學院，浙江 杭州 310018)

拉索索力測量方法主要包括：千斤頂油壓表讀數法、壓力傳感器測試法、磁通量測試法及振動頻率測試法。

在各類測量方法中，千斤頂油壓表讀數法和壓力傳感器測試法僅可用于施工階段拉索張拉時的監測，無法用于成橋階段的索力檢測。而相較于前述測量方法，頻率法能夠靈活運用于各階段的橋梁索力檢測，在操作便捷的同時也保證了精度，擁有較為完備的測量體系，目前絕大多數工程都傾向于采用頻率法對橋梁進行索力檢測。

但在實際測量索力的過程中，頻率法使用的因素有多方面影響，包括拉索的抗彎剛度、邊界條件、計算長度、垂度以及測量溫度，頻率法發展至今誕生了諸多基于影響因素的索力計算理論和修正方法。鑒于上述情況，本文梳理了現有頻率法測量索力的研究進展，著重論述了各研究成果的優化原理，指明了各自的優點和局限性，歸納了不同方法的適用條件，并展望了頻率法在今后的研究趨勢。

1 頻率法索力測量原理

處于工作狀態的拉索會在諸如環境因素或人工激勵作用下發生微小振動，通過使用高分辨率的頻率傳感器以及對應的數據采集設備，可獲得拉索振動時的若干階自振頻率。再結合索力與拉索線密度、索長、自振頻率、邊界條件、抗彎剛度等的關系式得出拉索索力[1]。拉索索力計算公式基于以下假設：

(1)拉索垂跨比很小，不考慮垂度的影響；

(2)拉索只在豎向平面內振動，忽略水平方向的移動，且豎直方向的運動也是微小的；

(3)拉索的幾何形狀近似用拋物線表示[2]。

如圖1所示，取拉索任意一段微小長度作為微元體，其平衡方程如下：

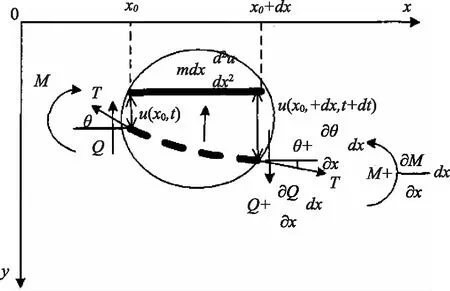
圖1 拉索微元體受力圖

(1)

(2)

式中，Q—剪力，N；M—彎矩，N·mm—拉力，N；u—y方向上的位移，mm。

根據梁彎矩和中和軸彎曲的曲率關系整理公式(1)和(2)可得到振動微分方程：

(3)

方程的解為：

u(x,t)=u(x)·y(t)

(4)

通過采取離散變量法最終可得到如下關系式：

y(t)=A1sinωt+A2cosωt

(5)

u(x)=Asinαx+Bcosαx+Csinhβx+Dcoshβx

(6)

式中，y(t)—時間函數；u(x)—振型函數；A、B、C、D—根據邊界條件確定的待定系數；ω—拉索的自振圓頻率，rad/s。其中：

(7)

式中，m—拉索單位長度質量，kg/m；T—拉索索力，N；EI—拉索的抗彎剛度，N·mm2。

上述推導過程采用了兩端鉸接的拉索模型，為滿足一般邊界條件的設定，在現有鉸接的基礎上，再在兩端支座處各添加一個彈簧約束，以此作為最終的力學模型。假定兩端彈簧鉸的約束剛度相同，k為彈性嵌固系數。此時拉索的邊界條件為：

(8)

將(8)代入方程(6)中，通過行列式運算和簡化最終得到了一般邊界條件下的拉索索力關于自振頻率的表達式：

k2[2αβ(1-cosαLcoshβL)+(α2-β2)
sinαLsinhβL]+2kEI(α3cosαLsinhβL-
α2βsinαLcoshβL+αβ2cosαLsinhβL-β3sinαLcoshβL)
-(EL)2(α2+β2)sinαLsinβL=0

(9)

由于上式的求解較為困難，在實測中缺乏便捷性，因此理論上只考慮簡支邊界的情況，并逐步發展成了最為通用的拉索索力計算理論，即張拉弦理論。

張拉弦理論在支座處僅考慮鉸接情況，拉索不受轉動約束，此時k=0，代入方程(9)中，并結合式(3)可得到索力的表達式：

(10)

式中，L—拉索的計算長度，m；fn—拉索第n階自振頻率，Hz；n—振動階數。

當忽略抗彎剛度時，公式則轉變為：

(11)

式(10)最先由Irvin[3]提出，是基于簡支理論推導的拉索索力計算公式，考慮抗彎剛度EI的影響，多用于短索索力計算，也是最基礎的索力計算模型；式(11)是實際運用最廣泛的經典索力計算公式，因其不考慮抗彎剛度，該狀態下的拉索為柔性，所以往往用于細長索的索力計算，結果也較為準確，計算過程多采用拉索的低階振頻。

從推導過程能夠看出，經典索力計算公式是建立在簡支邊界條件下的，但是實際拉索的邊界條件多處于簡支和固支之間，亦或是完全固支，直接將該公式運用于所有類型拉索的索力計算中難免會造成誤差，另外計算長度L的取值準確程度也會影響到計算結果，拉索自身的抗彎剛度、垂度以及所處環境的溫度都會直接影響到索的振動頻率fn，進而影響索力，因此有多項研究探討了上述因素在頻率法中的影響。

2 應用中的修正

2.1 邊界條件影響

在索體系的橋梁當中，拉索的連接方式主要有銷栓式和承壓式，兩類連接方式的共同點為各自端部至少有一側可等效為固支，因此必須考慮邊界條件對索力的影響，固支梁理論便是對這一構造特性的論證。

Zui[2]提出的固支梁理論就是在方程(9)中考慮k=∞的情況，此時拉索的轉動約束被視作無窮大，可將邊界條件視作固支。

為方便計算，在此過程中引入了參數ξ和C。

(12)

(13)

ζ為無量綱參數，也稱作拉彎比，用于表示拉索的動力特性與張緊弦的接近程度，取值越大接近程度越高，抗彎剛度影響也越小。

根據ξ取值范圍的不同和所測得的拉索不同階振動頻率，Zui等[2]通過曲線擬合的方法得出了拉索索力-振頻的關系式：

(1)采用一階振型頻率計算時：

(14)

(2)采用二階振型頻率計算時：

(15)

(3)采用高階(三階及以上)振型頻率計算時：

(16)

上述固支梁理論為后續索力公式的改進提供了依據，國內學者也提出了眾多基于固支梁理論下考慮拉索邊界條件的索力計算公式：

任偉新等[4]采用能量法和曲線擬合，建立了分別考慮索垂度和抗彎剛度影響由基頻計算索力的公式：

(17)

陳淮等[5]采用數值計算和曲線擬合，推導出了考慮吊索抗彎剛度和吊索兩端邊界條件影響的索力計算公式：

(1)采用一階振型頻率計算時：

(18)

(2)采用三階振型頻率計算時：

(19)

安振源等[6]使用迭代法和曲線擬合方法，建立了索力與一階振動頻率的關系式：

(20)

以上代表性理論皆是基于兩端固支的邊界條件考慮的，一定程度上彌補了早期國內索力計算領域的空白，雖然顧及了邊界條件但缺陷也是明顯的，例如邊界條件的定義存仍在理想化情況，采用高階頻率計算時精度難以把控，公式運用也并非十分方便。

為了提高頻率法公式的便捷性，甘泉[7]采用了將固支歐拉梁的振型函數作為兩端固接的振型函數：

φn(x)=[cosh(ax)-cos(ax)]-
En[sinh(ax)-sin(ax)]

(21)

(22)

根據上述條件研究建立了一套較為便捷的可用于固支和簡支邊界的拉索索力計算公式，相較于經典固支梁理論的振型函數，采用歐拉梁振型函數可降低公式的復雜程度，但所基于的邊界條件仍為固支。

對于實際服役的橋梁而言，拉索邊界條件多介于鉸支和固支之間，拉索端部或多或少會受到抗彎剛度影響，而技術人員在計算拉索索力時習慣于考慮單一的邊界狀態，由此必將造成檢測結果的偏差。

劉文峰等[8]從拉索實際的邊界條件出發，提出了固支和簡支耦合形式的振型函數：

(23)

(24)

式中，r—振型的階數；l—拉索計算長度，m；k—固支振動和簡支振動的一個比值，其大小代表了固支在邊界中所占的比重，可在后續求解索力的過程中求得。研究最終基于耦合邊界形式的振型函數給出了拉索索力-剛度關系式，方法較好地考慮了拉索實際的端部情況，精度優良，但計算過程仍略顯復雜。

孫永明等[9]在指出工程實際拉索與理想勻質拉索模型區別的基礎上，研究了端部性質對頻率法的影響，并最終建立了可計入端部性質影響的修正索力計算公式：

(25)

2.2 抗彎剛度影響

抗彎剛度對索力的影響主要體現在索長較短或索徑較大的拉索上。從構造角度出發，拉索是由數根平行的鋼筋、鋼絲或鋼絞線經小角度扭絞形成。若拉索的鋼絲之間完全滑移，則拉索慣性矩就是各根鋼絲的慣性矩之和；若拉索的鋼絲之間完全粘結，即各根鋼絲形成了一個整體，則索的慣性矩為等截面鋼棒的慣性矩，兩種假設的結果相差較大。而實際工程中拉索內部構造往往介于彼此分離和完全粘結之間，嚴格意義上來說拉索的抗彎剛度是一個未知量。

蘇成等[10]采用有限元法及樣條擬合技術獲取了拉索索力與頻率的對應關系，提出一種基于多階頻率測試結果的斜拉索抗彎剛度識別方法，通過實測數據分析得出了拉索的實際抗彎剛度為0.37(EI)max,其中(EI)max為索按全截面計算時的抗彎剛度。

但是實際拉索的抗彎剛度并不是一個恒定的值，會因其他參數的改變而發生細微的變化，例如索力和溫度，因此在探尋抗彎剛度對索力影響的過程中，不少學者另辟蹊徑，提出了一種避開抗彎剛度求算索力的思路，如孟少平等[11]運用能量方法建立了索力、抗彎剛度和固有圓頻率之間的關系：

(26)

式中，φ(x)—振型函數，通過建立一端鉸支一端固支的振型函數，配合聯立1階和2階固有圓頻率的表達式ω1和ω2，可消去抗彎剛度EI，并最終得到索力關于前兩階固有振頻的計算式：

(27)

上式將抗彎剛度作為隱式參數計算，回避了工程中拉索抗彎剛度難以識別的問題，在無法精確獲取抗彎剛度的情況下優勢顯著；同樣，袁博等[12]也利用能量法，提出了在拉索抗彎剛度未知的情況下，用于計算拉索索力的計算方法；Seyed等[13]在推導考慮剛度影響的索力計算公式時也選擇了規避抗彎剛度的方法，但采用的原理并非能量法，首先計算拉索實測頻率和計算頻率間的差值，將該差值定義為關于剛度EI和索力H的誤差函數E，再通過E求得一階固有振動頻率后，即可計算出索力。

當不考慮規避抗彎剛度時，Chen等[14]通過對一系列纜索進行抗彎剛度實驗后得出結論，纜索的抗彎剛度會隨著索兩端張拉力的增大而增大；而張永平等[15]進一步提出纜索抗彎剛度與拉力的非線性關系模型：

ω2=n2π2T/mL2+n4π4EI/mL2

(28)

式中，ω—纜索的振動頻率，Hz；n—振頻階數。上式可用于頻率法中拉索抗彎剛度的修正，但仍需針對不同的邊界條件進行更深入的研究，完善抗彎剛度的修正模型。

燕啟清等[16]建立了一種考慮短吊桿抗彎剛度的索力計算公式：

(29)

(30)

(31)

式中，f1—吊桿一階振動頻率，Hz；TQ—標定吊桿索力比例系數時的千斤頂張拉力，N；Tb—第一次張拉階段吊桿張拉力設計值，N；Ts—成橋后吊桿索力設計值，N；λ—吊桿邊界條件修正系數；C—吊桿橫向抗彎剛度修正值；K—吊桿索力比例系數；η—吊桿索力偏差系數。

η=1-Tb(Ts+C)/Ts(Tb+C)

(32)

當|η|≤Δ時，可不考慮吊桿橫向抗彎剛度對索力的影響；當|η|≥Δ時，必須用式(32)進行索力修正，此時將被修正的吊桿定義為短吊桿，橫向抗彎剛度對索力的影響不可忽略，Δ的值則根據相應的技術規范取定。

2.3 計算長度

有關拉索計算長度的研究本質上是由邊界條件引申而出的一類子問題，由于邊界剛度的存在，在計算拉索索力時無法取整段索長作為實際的計算長度，取值的關鍵在于精確判別端部抗彎剛度限制拉索有效振動的范圍。

拉索通常是由：套筒、錨杯、中部自由振動的索體3部分組成，如圖2所示。錨固區域具備較大的剛度，能夠有效限制振動，但是其限制自由部分振動的能力不顯著，在索力計算時索長可取拉索能振動部分的長度，設計文件中一般為拉索兩端錨墊板之間的距離[17]。陳陽[18]通過采用牛頓切線法迭代計算有效長度的方法，得出吊索計算長度可取為上下錨固點之間的理論長度，驗證了設計規范中的內容，但是其實驗對象為9～38m的吊桿，且實測數據表明索力誤差可達8%，精度尚待提高。而且在長度更大或是具有一定垂度的拉索有效長度取值中該方法或許并不適用。

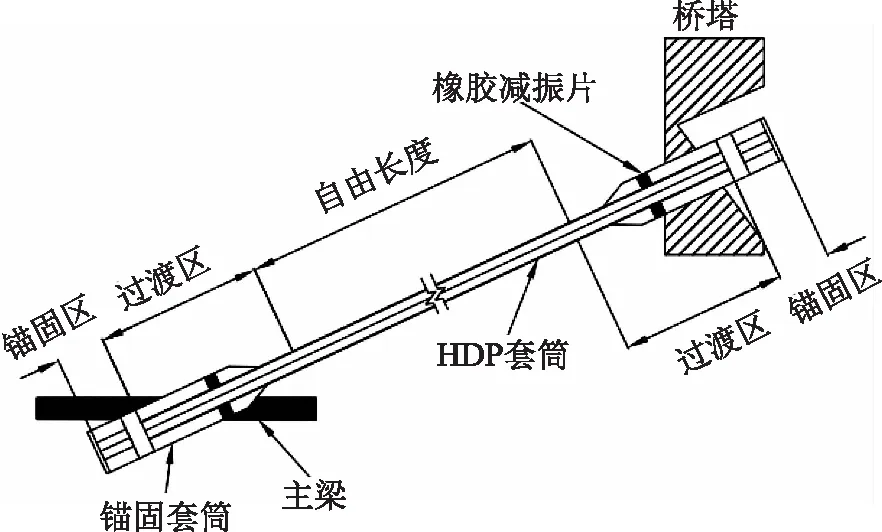
圖2 拉索構造示意圖

經有關學者實驗分析得出，拉索有效長度取值的精確程度對長索的影響較小，但對短索的影響較大，有數據表明誤差最高可達66%[19]，這就意味著在面對短索索力的計算時要更為嚴格地取定拉索有效振動長度。

宋一凡和賀拴海[20]引入了動力計算長度的概念，解決了用振動法測估索力時面臨的有效索長取值難題，提出了基于二階固有頻率的動力計算長度lde的實用公式：

(33)

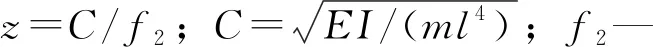
為減緩拉索振動，保證橋梁整體的穩定性，在實際布置拉索時一般會在套筒內安裝減振片等阻尼裝置，或是在外部安裝減振器。減振器的設置會縮短拉索的自由振動長度因此需重新定義有效長度，胡利平和林育洪[21]采用的方法是分別測取拉索安裝減振器前后的頻率，再利用2次頻率值的不同來換算索長：

(34)

式中，l′—換算后的索長，m；l—實際索長，m；fn、f′n—安裝減振器前后的某一階拉索振動頻率，Hz，一般可取基頻。假如事先沒有進行該項操作，則可先取拉索上下減振器之間的長度作為計算長度再適當估計結果誤差范圍進行調整的辦法。相較于其他理論，采用此方法的分析結果較快捷，具備一定的工程推廣性，但并沒有針對不同邊界條件的拉索進行公式的細化，在使用過程中也難免會產生誤差；林天然[22]在采用張拉弦理論計算索力的基礎上提出用吊桿計算長度的修正值對索力進行修正，通過對某一大跨度拱橋吊桿進行索力測試，最終確定修正值為減振器到錨固端距離的0.9～1.1倍之間，該法同樣是一種快捷的計算長度修正手段，但在特殊情況下也同樣面臨著精度不足的問題。

Li[23]根據能量法發展了一種基于附加質量塊的有效長度確定方法，得到了固有頻率和有效長度間存在的解析關系：

(35)

式中，ω1、ωm1—施加質量塊前后拉索的一階固有振頻，Hz；m—拉索的單位長度質量，kg；M—質量塊的質量，kg。Li將該公式運用于某吊桿拱橋的索力檢測中，通過與實測值進行比對顯示此方法可將索力誤差控制在5%，在短索中的預測精度表現較為出色。

當面對具有一定垂度的長拉索時，基于拋物線理論的長度計算法是設計中普遍采用并且認可度較高的方法，但隨著拉索長度的增加，垂度的非線性影響會不斷增大，傳統拋物線理論的計算精度會因此受到影響，考慮到這一問題，孟慶成等[24]提出采用懸鏈線公式來計算斜拉索的無應力長度，長度的計算公式為：

l0=l-Δl

(36)

(37)

(38)

式中，l0—拉索無應力長度，m；H1—拉索下錨點拉力的水平分量，N；gcb—拉索的單位長度重量，kg/m；a—上下錨點之間的水平距離，m；λ1—下錨點處拉索切線與水平的夾角。實測結果顯示，該公式下的各階頻率估算的索力波動較小，改進了用拋物線法近似求解索長的傳統方法，可用于大跨度橋梁的拉索計算中。

除上述理論外，學者們在研究過的程中也建立了眾多從不同原理出發的，關于計算拉索有效長度的實用公式。周正茂[25]提出了振型節點法，利用3階以上模態振型的中間節點間距作為計算長度，該方法的優點在于回避了復雜的邊界條件，原理簡潔思路新穎，可直接運用于公式(10)中，以三階模態為例，選取三階模態頻率f3作為計算頻率，取中間相鄰2個模態節點間的距離作為計算長度L，因為此時只取了一段距離，所以階數n取為1，在更高階模態中n可取2或更大，L也要進行相應調整。方法的不足之處在于其精度易受索長、振型階次和邊界條件的影響，仍有很大的改進空間。

史杰[26]通過建立靜載試驗前后吊桿索力差和頻率差的解析式，反推得出了索力計算長度的表達式：

(39)

其中：

(40)

(41)

式中，n—振動階數；ρ—拉索線密度，kg/m；δT—加載前后索力的增量，N；fn,1、fn,2—加載前后對應的n階振動頻率，Hz。由公式(41)可知索力增量和頻率平方差成正比，因此Kn可通過拉索加載前后的索力增量和頻率數據擬合得到。此方法原理簡單，操作步驟簡潔，可運用于新舊橋梁的索力檢測。

2.4 垂度影響

實際許多的橋梁拉索會呈現出下垂的狀態，呈現出很強的非線性性質[27]。拉索垂度的成因包括：索力、索長、自重、傾角等，垂度的存在對拉索的最直接影響就是其振動頻率。在拉索長度確定的前提下，拉索垂度對基頻的影響較大，但是對高階頻率(四階及以上)的影響較小。

早期的研究例如島田忠幸[28]通過引入參數Γ來量化拉索垂度對固有頻率的影響：

(42)

Irvine[3]通過推導微元體平衡方程，提出了用無量綱參數λ2考慮拉索垂度對索力的影響，該參數也成為了拉索弦振動理論中的基本參數之一：

(43)

(44)

參數λ2反映的是索的垂度和彈性模量對基頻的影響，具體表現為當λ2較大時，索力較小，拉索的垂度較大，對基頻的影響也較大，反之則越小。

由于直接采用λ2求解無法解得特定垂度下索力與振動基頻的關系式，因此往往用能量法近似來實現這一目標，得到的考慮垂度的索力-基頻的關系式如下：

(45)

式中，ω—拉索振動的基頻，Hz；H—索力的弦向分量，N；l—拉索計算長度，m；m—拉索單位長度質量，kg/m。最終可以得出考慮索垂度和彈性影響的索力計算實用公式[29]：

(46)

上述公式在行業方面的認可度高且較為基礎，但在拉索振型的考慮上存在局限，只是給出了基于基頻的索力公式，并未考慮拉索垂度對更高階振動頻率的影響。

李國強等[30]通過驗證各因素對索力檢測的影響得出結論：垂度只影響索的奇數階振頻，尤其反映在一階頻率上，對高次奇數階頻率的影響較小，對偶數階頻率的影響可忽略不計。在涉及垂度作用下的拉索頻率選取中，該結論有著重要的參考價值。

同樣，在處理垂度對不同階頻率的影響時，冉志紅和李喬[31]通過采用奇異攝動解法這一種求解微分方程近似解析解的方法來求解拉索的動力平衡方程，給出了考慮拉索垂度影響的索力計算公式：

(47)

其中：

(48)

劉志軍[32]在研究用垂度修正索力的過程中，提出了采用傳遞矩陣法考慮垂度對拉索索力的影響，該方法基于拉索的微元體靜力平衡方程，將拉索分為了n+2個質點和n+1個沒有質量只有張力的弦，建立了求解索力的矩陣方程，方程的關鍵點在于修正垂度影響下的拉索自振頻率，進而使得索力預測的結果更加準確。傳遞矩陣法易于編程且精度可靠，在實際工程中具備快速測量的優勢。

相較于用垂度修正索力，運用拉索垂度特性反求索力也是一條新思路，葛俊穎等[33]通過有限元軟件分析證明了當斜拉索的索力較大時，其拉索中部位置的索力和垂度存在著確定的函數關系，且不受拉索本身剛度和兩端支承條件的影響。當選取一定長度的中間索段時索力的計算公式為：

(49)

式中，TM—該索段的平均索力，N；T0—最小索力，N；TL—最大索力，N，分別位于該段的最上端和最下端；L—索段的索長，m；α—對應的傾角；fmax—最大垂度，后3項參數可由儀器測得，最后根據該段拉索的各項索力可確定整條拉索的索力情況，選取的索長越大結果越精確，且不受抗彎剛度和邊界條件的影響。

2.5 測量溫度影響

從拉索自身溫度效應出發，拉索長度會隨材料的熱脹冷縮而產生細微的改變，從而造成索力和頻率的變化；整體上，橋梁拉索通常由鋼材制作而成，與之錨固的主梁則大多為混凝土構件，材料間不同的膨脹系數決定了二者在同溫度變化下的變形存在差異，變形速率也不同，整體結構的部分變形不一致也導致了索力隨溫度的變化，而實際的情況更為復雜，橋梁的溫度日變化幅度呈現出：氣溫>拉索溫度>梁、主塔溫度的梯度狀況，這使得索力關于溫度的變化值變得更難以捕捉。

一座橋梁在正常的大氣環境中會經歷酷暑和嚴寒，年溫差通常會超過50℃。溫差會對頻率造成影響進而影響索力，同時也會對垂度造成影響，所以拉索的索力、垂度、振動頻率、環境溫度之間的關系是復雜的，關鍵就在于能否將溫度的影響準確量化，因此國外學者Kim[34]和Park[35]開始嘗試一種能夠結合更復雜因素的參數敏感性方法(PSM)來識別多因素影響下的索力。

國內方面，候俊明[36]曾對某一單索面斜拉橋進行索力監測，實測結果顯示拉索索力會隨著溫度而異，在室外時隔4h的索力變化幅度可達到2.5%，由此可見溫度對于索力的影響不可忽略。但研究并沒有給出基于溫度變化的索力計算公式或修正方法，同時缺少了溫度對其他結構參數影響的討論。任遠[37]嘗試用限元模型對拉索進行溫度效應的監測，雖然能夠有效反映索力的變化趨勢，但在施工控制中只能作為一種近似的手段。

在獲取了索力隨溫度變化趨勢的前提下，Chen[38]采用總體經驗模態分解法(EMD)對索力、環境溫度、索溫變化量的時域圖進行時程分析，研究了基于環境氣溫和拉索索溫變化量的索力修正系統，并在EMD的基礎上更進了一種基于噪聲輔助的數據分析方法(EEMD)，方法取得了顯著的效果，較大程度地消除了拉索的溫度效應，但該技術的難度較大且局限于低塔斜拉橋的橋型，目前仍位于改進階段。

考慮到需要建立一種可供現場快速使用的公式方法，Ma等[39]采用有限差分法來處理拉索動力方程中溫度的影響，并最終求得了索力關于溫度變化的數值解，但是公式仍較復雜；艾玉麒[40]提出了一種基于溫度的索力變化量公式：

ΔT1=KαEA(t1-t)

(50)

式中，K—溫度修正系數，可由相應的有限元模型計算得到；α—線膨脹系數；t1—實時溫度，℃；t—設計溫度，℃。對比文獻[39]的公式，該方法原理簡明且相關參數易被采集，在涉及溫度的索力修正中其運用更加便捷。

3 總結

本文通過總結影響頻率法索力測量的5項因素，得出以下結論：

(1)定義單一邊界條件的做法較為理想化，與實際不符。基于耦合邊界條件的剛度識別法能夠求得更貼近真實的拉索振型函數，使結構分析更加合理。

(2)抗彎剛度對索力的影響主要針對短、粗拉索，可采用剛度修正公式、剛度系數折算法對抗彎剛度進行求解。當剛度難以測取時，可采用回避剛度的隱式索力計算法。

(3)計算長度對索力的影響主要針對端部約束大、長度短的拉索，根據經驗公式選取自由振動長度的方法雖快捷但不適用于短索，可采用基于固有振頻的有效振動長度計算法獲取計算長度。

(4)垂度的影響對象為長拉索，在面對具有一定垂度的拉索時應盡量選取高階偶數階振頻計算索力。后續關于垂度的研究將逐步擺脫階數的限制，使得各階頻率計算下的索力結果都趨于穩定。

(5)溫度影響的量化難度較大，不同構件關于同一溫度變化所產生的溫度變形各不同。故測量索力時應盡量避免在溫度較高的正午進行。現有頻率法中關于溫度影響的研究仍不成熟，未來需持續更進。