GeoGebra環境下基于范希爾理論的雙曲線及其標準方程教學研究

◇遼寧師范大學數學學院 于茹子 吳 華

智能時代的教育教學變革需要信息技術與教學活動的深度融合，借助GeoGebra動態幾何軟件的優勢，以“雙曲線及標準方程”為例，經過范希爾理論的學前診斷、引導定向、闡明、自由定向、整合五個教學階段，幫助學生發現幾何規律，理解幾何本質，提高幾何思維水平。

新版《普通高中課程標準（2017版）》對教育信息化提出說明：“信息技術是學生學習與教師教學的重要輔助手段，為師生交流、生生交流、人機交流搭建了平臺，為學習和教學提供了豐富的資源。因此，教師應重視信息技術的運用，優化課堂教學，轉變教學與學習的方式[1]。”美國《國家人工智能研發戰略規劃》中也提到要利用人工智能技術改進教育機會，實施個性化學習和終身學習等[2]。

在宏觀政策要求下，智能時代教育教學的變革需求使信息技術與教學活動的深度融合迫在眉睫[3]。然而GeoGebra作為一個多功能動態幾何軟件，具有數學化、視覺化、動態化呈現數學對象與思維的功能[4]，同時它能夠做到幾何圖形與代數方程的同步變化，幫助學生發現幾何規律，理解幾何本質[5]。現已被世界各國廣泛應用在數學課堂教學中，它豐富了課堂活動，拓展了學生思維，改變了教學現狀。

范希爾理論不僅能夠評估學生的幾何思維發展現狀，還可以設計教學階段進而提高學生的幾何思維水平。范希爾認為，學生幾何思維的發展具有先后順序[6]，設計教學需要依據“順序性”原則，遵循學生的認知結構。基于此，本文以“雙曲線及其標準方程”為例，借助范希爾理論對幾何教學進行思考，并結合GeoGebra，旨在促進技術在數學教學中的改革。

1 范希爾理論

20世紀50年代，范希爾夫婦在日常教學中發現幾何教學存在的問題，并受皮亞杰認知發展階段論的啟發，提出了幾何思維的五個水平與對應的五個教學階段[7]。筆者梳理了范希爾理論并做出結構示意圖，如圖1所示。

圖1 范希爾理論示意圖

五個思維水平分別為：①層次0—視覺，學生能根據外觀辨識圖形，在心理上把圖形表示成直觀圖像；②層次1—分析，學生能確定圖形的性質，辨別圖形的特征；③層次2—非形式化的演繹，學生能提出非形式化的推論，形成抽象的定義；④層次3—形式化的演繹，學生能通過形式化的推理，建立定理；⑤層次4—嚴密性，學生形成了更高的思維水平，能在不同的公理系統下建立定理并分析其特性。

五個教學階段分別為：①階段1—學前咨詢，課前教師通過雙向交談的方式了解學情，幫助學生理解所要學習的內容；②階段2—引導定向，教師幫助學生安排活動順序，這個過程中學生逐漸確定學習的方向；③階段3—闡明，通過前面的活動經驗和教師的提示，學生能夠明確表達自己的看法；④階段4—自由定向，學生在解決復雜問題的過程中獲得經驗，確定自己學習領域的方向；⑤階段5—整合，學生將所學到的方法內化到自己的思維結構中去，形成一個新的思維領域。

本文主要針對“雙曲線定義及其標準方程”這一部分內容，依據范希爾理論設計更符合學生幾何認知發展的課程，結合動態幾何軟件的優勢，通過折紙實驗與雙曲線定義的推導，發展學生的幾何思維，有效改善傳統的幾何教學。

2 GeoGebra動態幾何軟件

GeoGebra是由美國佛羅里達州亞特蘭大學的數學教授Markus Hohenwarter所設計的，這是一款結合幾何、代數與微積分的免費、多平臺的動態數學教育軟件[8]。GeoGebra最大優勢就是其能夠動態展示數學對象的生成過程，幫助學生在“變化”中找到“不變”的幾何規律。其次就是它能夠做到“數”與“形”的同步變化，通過構建“數”與“形”之間的聯系通道，幫助學生跨越知識符號，建立內在的邏輯和意義[9]。而數形結合思想是數學學習中的重要思想，華羅庚曾有詩云：“數與形，本是相倚依，焉能分作兩邊飛。數缺形時少知覺，形少數時難入微。數形結合百般好，隔離分家萬事非。切莫忘幾何代數統一體，永遠聯系，切莫分離”[10]。充分說明了數形結合的重要性，這也是GeoGebra軟件的優越性所在。

GeoGebra軟件有其獨特的功能與特點，圖2[11]為筆者整理的結構模型，可以幫助讀者加深對GeoGebra的了解。

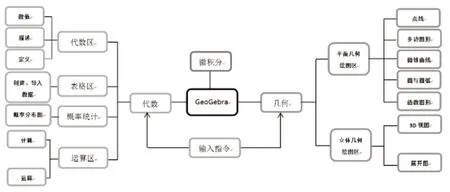
圖2 GeoGebra結構模型圖

本文通過運用GeoGebra軟件對“雙曲線及其標準方程”這一部分內容進行教學設計重構，希望彌補傳統解析幾何教學的局限性，培養學生對于解析幾何的興趣，促進學生的直觀思維向抽象思維過渡，提升課堂教學的實效性。

3 基于范希爾理論的“雙曲線及其標準方程”教學設計

3.1 教學內容分析

雙曲線是高中數學人教B版選修2-1第二章“圓錐曲線與方程2.3”的內容，一般安排三個課時，本節課是第一課時[12]。它是繼學習橢圓之后的又一種圓錐曲線，也是我們高中解析幾何部分的重要內容之一。接下來依據范希爾理論并且融入GeoGebra，對“雙曲線及其標準方程”進行了幾何思維水平的劃分，如表1所示。

表1 “雙曲線及其標準方程”的幾何思維水平劃分

3.2 GeoGebra環境下依據范希爾理論的雙曲線教學設計

階段1：學前咨詢—復習引入，初識雙曲線

師：通過上節課的學習，對于橢圓你掌握了什么嗎？

生：利用拉線作圖掌握了橢圓的定義，利用邏輯推理獲得了橢圓的標準方程，在推導標準方程過程中明確了建系的方法。

師：大家對于橢圓有了一定的了解，這節課我們繼續探索另一種圓錐曲線—雙曲線，請看大屏幕。

師：在現實生活中，我們經常可以抽象出雙曲線的形狀，通過知網檢索也可以發現，雙曲線在許多我們熟知的領域都有應用，雙曲線究竟有什么魅力以至于它有如此廣泛的存在與應用呢，今天我們就來探尋一下雙曲線的形成吧！

設計意圖：①這一環節屬于范希爾理論幾何教學階段的學前咨詢階段。②教師通過與學生的雙向交談，了解學生關于圓錐曲線的認知結構。③教師通過PPT引入生活中的雙曲線，使學生通過幾何的直觀感知、初識幾何體，明確數學來源于生活并高于生活。

階段2：引導定向—直觀想象，雙曲線定義的猜想

探究1：雙曲線的定義。

師：在前面“橢圓的幾何性質”學習中已經知道，在半徑為r的圓F1內取一定點F2，折疊紙片使圓周上的某一點A剛好與點F2重合，折痕為L。連接AF1交L于點M，點M的運動軌跡就是橢圓，如圖3所示。

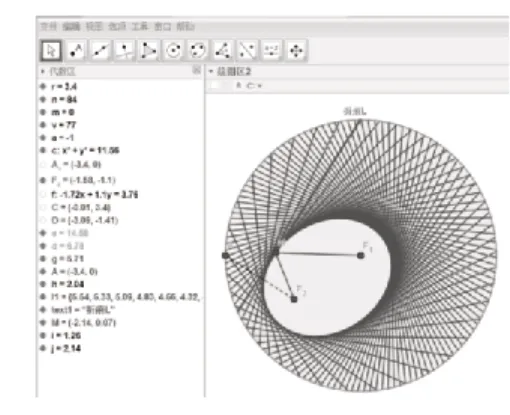
圖3

問題1：如果將上述問題中的條件“在圓內取一定點F2”改為“在圓外取一定點F2”，那么點M的運動軌跡又會是什么呢？

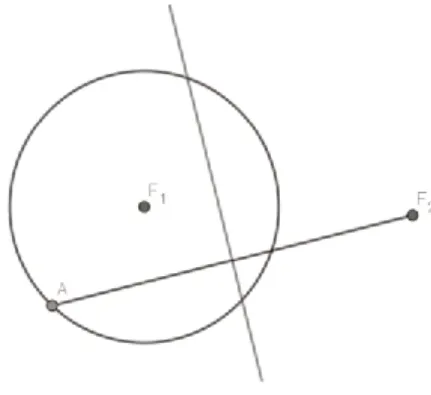
圖4

師：通過自己的動手實踐，大家發現點M的運動軌跡是什么了嗎？

生：雙曲線。

師：由于折紙無法取遍圓上所有的點，所以老師借助GeoGebra軟件動態展示雙曲線生成的全過程。

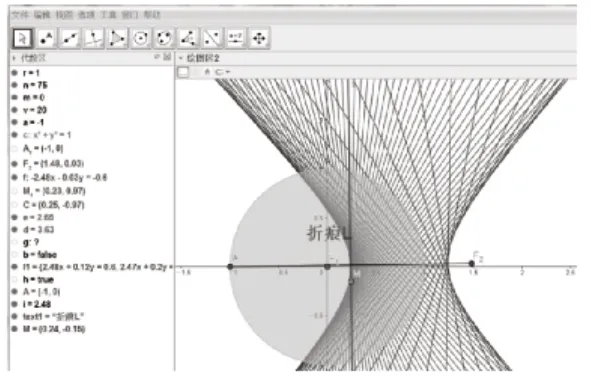
圖5

師：大家通過觀察圓片折疊形成雙曲線的過程，能夠發現各線段間存在什么關系嗎？

生：點A與點F2通過折疊重合，并形成了折痕L，所以折痕L為線段AF2的垂直平分線。點M是折痕L 與半徑AF1延長線的交點，根據軸對稱的性質，MA=MF2。

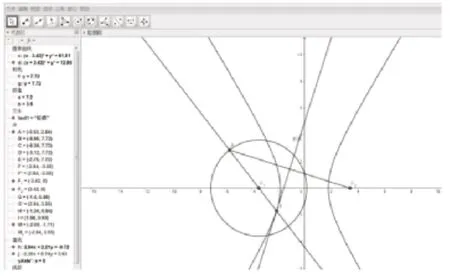
圖6

問題2：動點M到兩定點F1、F2會形成什么關系式？

師：前面的學習中已經知道“平面內一動點到兩定點距離之和是定值的點的軌跡是橢圓”，大家能否觀察圖形，抽象出雙曲線的定義呢？

生：平面內一動點到兩定點距離之差是定值的點的軌跡是雙曲線。

師：你是怎么抽象出來的？

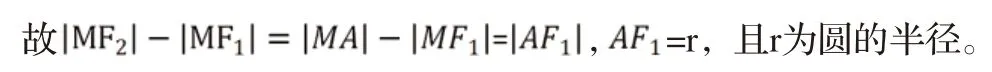
師：這樣就得出了“動點M到兩定點F1、F2的距離之差是定值”的結論。

問題3：MF2與MF1之間需要滿足什么關系式呢？

師：這是交點M在圓內的情形，如果交點M在圓外呢，上述得到的關系式還能否適用？

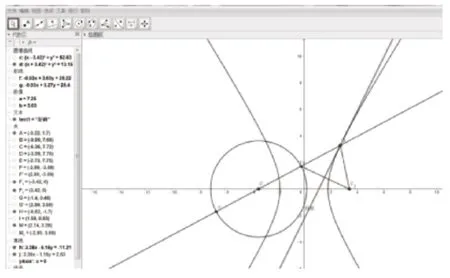
圖7

設計意圖：①這一環節屬于范希爾理論幾何教學階段的引導定向階段。②教師運用GeoGebra動態生成雙曲線的形成過程，通過構造動點，觀察“數”與“形”的同步變化，為猜想雙曲線定義提供技術支持。③教師通過問題鏈的形式，一步步引導學生思維的深入。④基于此階段的教學設計，學生通過自主探究、分析、推理，最終獲得雙曲線的關系式，達到提升學生幾何思維水平的目的。

階段3：闡明—邏輯推理，雙曲線定義的獲得

問題5：雙曲線的定義是什么？

師：通過上述得到的關系式，能否總結其共性，給雙曲線下一個定義？

生：將平面內與兩定點F1、F2距離之差的絕對值是常數2a的點的軌跡叫雙曲線。

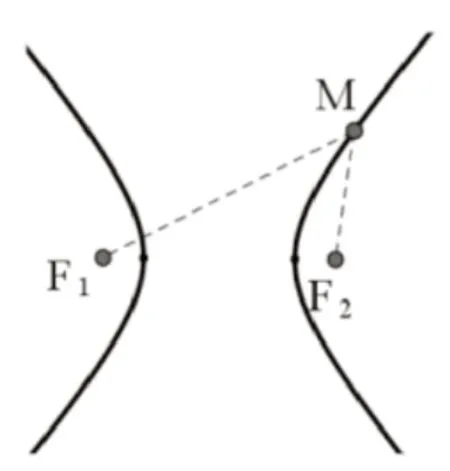
圖8

生：當2a=2c時，M點的軌跡是射線；當2a大于2c時，M點的軌跡不存在；當2a小于2c時，M點的軌跡是雙曲線。故要給2a一個限制條件，只有當軌跡才是雙曲線。

師：這樣我們就得出了雙曲線的完整定義：把平面內與兩個定點F1、F2的距離的差的絕對值等于常數2a（<）的點的軌跡叫做雙曲線。其中這兩個定點叫做雙曲線的焦點，兩定點間的距離叫做雙曲線的焦距。

設計意圖：①這一環節屬于范希爾理論幾何教學階段的闡明階段。②教師通過語言和技術的引導，向學生闡明雙曲線定義的內容和限定條件，使定義更加完整化、系統化。③學生則根據前面的經驗與教師的提示，推導出雙曲線的定義。④通過GeoGebra的直觀演示，將抽象的數學概念用直觀圖形來顯示，進而提高課堂教學的實效性[13]。

階段4：自由定向—數學建模，雙曲線定義的深化

探究2：雙曲線的標準方程。

問題1：回顧圓錐曲線的發展歷史，第一定義較原始定義有什么優點？

生：有了這個定義，方便我們寫出雙曲線的方程。

師：用方程研究雙曲線的性質，這是解析幾何學研究問題的手段。

問題2：回顧一下研究曲線方程的步驟是什么？

生：第一步是建系。

師：雙曲線應該怎么建系合理呢？

生：以F1F2的中點為原點建立直角坐標系。

師：坐標系建好后，我們設點就方便多了，大家可以把M、F1、F2的坐標點表示出來嗎？

師：如何根據這幾個點的坐標列式呢？

（由于時間原因，推導過程作為練習題在課前留給學生，自己探索解決辦法，教師挑出具有代表性的方法課上交流討論。）

師：怎樣讓方程變得更簡潔？

師：焦點在y軸上的標準方程需要大家自己動手完成。

設計意圖：①這一環節屬于范希爾理論幾何教學階段的自由定向階段。②這個階段學生能用演繹推理的方式得到雙曲線的標準方程，通過對雙曲線定義的應用，最終達到對于雙曲線定義的全面把握。③整個教學過程，師生共同參與，建構知識結構，完成方程的推導。

階段5：整合—數學運算，雙曲線定義的內化

例題1：已知，動點P到F1、F2的距離之差的絕對值為6，求P點的軌跡方程。

例題2：根據下列條件，求雙曲線的標準方程。

設計意圖：①這一環節屬于范希爾理論幾何教學階段的整合階段。②這個階段學生對雙曲線的定義的理解進入內化階段，能用雙曲線的知識解決問題，同時進一步體會了數形結合思想。③學生通過各種習題的練習，深化對于雙曲線定義及標準方程的理解，最終達到知識的遷移與靈活應用。

4 結束語

本文以范希爾理論與GeoGebra動態幾何軟件的結合為支點，充分發揮范希爾理論的理論指導和動態軟件的技術優勢，從生活情境入手，讓學生體會生活中的雙曲線，到通過折紙實驗和問題鏈的方式推導出雙曲線的定義與標準方程，最后內化知識并靈活運用知識解決問題，過程中學生逐漸加深對知識的理解，經歷獲得知識、深化知識、內化知識的過程，最終形成新的思維領域。整個過程遵循學生的思維結構，從特殊到一般，具體到抽象，學生一步步將知識內化到自己的認知結構。其中在GeoGebra軟件的技術支持下，培養學生的幾何直觀能力，縮小教學內容的思維水平與學生實際的思維水平間的差距，幫助學生進行形式化的演繹推理[14]。