基于智能垃圾箱回收閾值的回收車輛路徑問題

文/孟亞雷

本文針對智能回收車輛路徑問題，考慮了智能垃圾箱回收閾值對回收公司運營成本的影響，構建了回收公司運營成本最小化的優化模型，并運用PSO粒子群算法進行車輛路徑優化，并結合實例對模型和算法的有效性進行了驗證。結果表明，回收公司通過確定合理的垃圾箱回收閾值進行車輛優化調度，可以有效降低回收運營成本，進而為智慧城市回收物流網絡建設提供了理論借鑒。

1.問題描述

隨著城鎮化進程的加快與居民消費水平的提高，居民生活垃圾與日俱增，“垃圾圍城”現象普遍存在，并成為新一輪城鎮化發展的制約因素[1]。近年來，國家大力推動城市環衛系統與再生資源系統的兩網融合，以減少資源消耗，降低環境污染。一種基于物聯網技術的智能垃圾箱應運而生[2]。智能垃圾箱可以實施監測箱體內廢棄物的填充狀態，當達到一定的閾值后，回收公司派遣車輛進行清理。而不同的回收閾值將導致待清理的智能垃圾箱數量與廢棄物回收量有所差異，對車輛調度與路徑優化提出了更高的要求[3]。在車輛數量一定的情況下，為了提高回收效率并節約回收運輸成本，需要綜合考慮垃圾箱回收閾值對車輛調度的影響，進行合理的回收車輛路徑優化問題研究。圖1展示了基于智能垃圾箱回收閾值的回收車輛路徑優化前后對比。

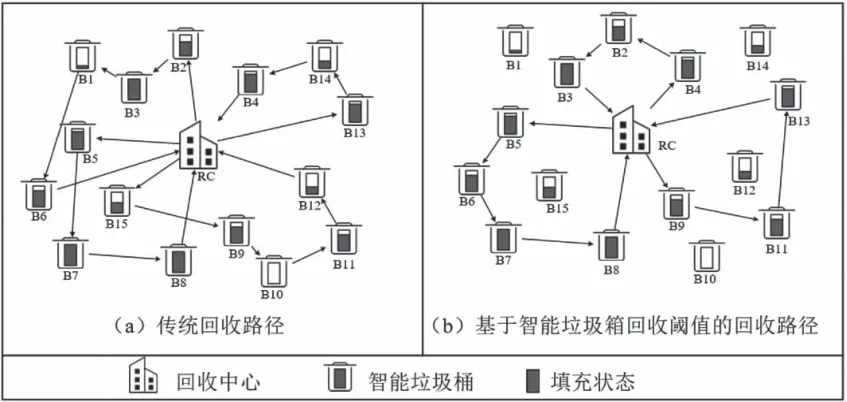
圖1 基于智能垃圾箱回收閾值的回收車輛路徑優化前后對比

由圖1可知，圖1（a）表示傳統回收路徑下，回收公司統一清理服務范圍內的智能垃圾箱，由于部分垃圾箱內廢棄物數量較少，回收公司派遣車輛進行清理，使得回收效率低下，且回收網絡中存在長距離運輸與交叉運輸等現象，增加了回收運輸成本。圖1（b）表示基于智能垃圾箱回收閾值的回收路徑，回收公司預先設定合理的回收閾值，當智能垃圾箱內廢棄物填充狀態達到回收閾值后，回收公司派遣車輛進行回收，并結合智能垃圾箱的分布情況與達到回收閾值的時間進行合理的路徑優化，節約了廢棄物運輸成本，并提高了回收效率。

2.模型建立

基于智能垃圾箱回收閾值的回收車輛路徑問題可表示為G=（N0，A）的無向圖，N0為圖中所有回收節點的集合，包括垃圾箱N與回收公司0，A為圖中任意節點間弧的集合，xijv為0-1變量，當車輛v由節點i行駛至節點j時，xijv=1，否則，xijv=0。Uv為車輛v服務的智能垃圾箱的集合，V為所有車輛的集合，Dij為回收節點i與回收節點j之間的距離，fv為單位距離油價，o為回

收公司預先設定的回收閾值，mj表示智能垃圾箱的容量，qv表示車輛容量，L為車輛行駛最大距離，Q為回收公司處理能力，|Uv|為車輛v服務的智能垃圾箱的數量，[ej，lj]為智能垃圾箱回收時間窗，ajv為車輛到達節點j的時間，div為車輛離開節點i的時間，tijv為車輛由節點i行駛至節點j的運輸時間，λe為車輛早于垃圾箱時間窗到達回收點的單位時間懲罰成本，λd為車輛晚于垃圾箱時間窗到達回收點的單位時間懲罰成本，kv為車輛租賃成本，δv為車輛維修成本，ρ 為回收品固定處理成本，σ 為回收品變動處理成本，wjv為車輛在節點j的等待時間，W 為無窮大常數。本文以回收公司運營成本最小化為目標，建立基于智能垃圾箱回收閾值的回收路徑優化模型，如式（1）所示。

式（4）表示任一智能垃圾箱只能由一輛車進行服務，式（5）為流量守恒約束，式（6）為車輛容量約束，式（7）為車輛行駛距離約束，式（8）為回收公司處理能力約束，式（9）表示消除了車輛行駛子回路，式（10）-式（12）為車輛到達垃圾箱所處回收點的時間約束，式（13）為變量約束。

3.PSO粒子群算法

車輛路徑問題是由Dantzig和Ramser于1959年首次提出，屬于典型的NP-hard問題，學者們傾向于采用啟發式算法進行求解。PSO粒子群算法是模擬鳥類捕食行為的一種智能優化算法，經常被用于求解路徑優化問題[4]。粒子群算法搜索過程中，每一個粒子都表示一個優化解，擁有速度和位置兩個屬性。其中，離子飛行速度根據粒子搜索過程中的最優解（局部最優）和種群搜索過程中的最優解（全局最優）進行動態調整。粒子速度與位置更新公式如下所示。

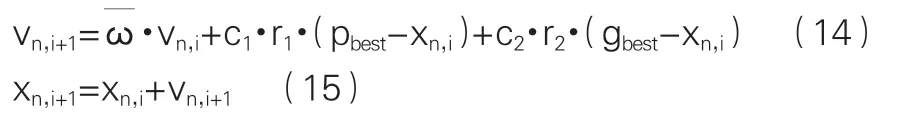
式（14）為粒子速度更新公式，式（15）為粒子位置更新公式。式（14）與式（15）中n=1，2，3，...，N；N表示種群中粒子的個數；表示表示粒子的慣性權重，是0-1之間的隨機數；vn，i表示在第i代搜索過程中粒子n的速度；c1與c2表示學習因子，一般c1=c2=2，r1與r2表示0-1之間的隨機數；pbest表示粒子搜索過程中的最優解（局部最優），gbest表示種群搜索過程中的最優解（全局最優）；xn，i表示粒子在第i代搜索過程中的位置。粒子群算法具體實施步驟如表1所示。

表1 粒子群算法步驟

4.實例分析

以智能回收公司A與其服務范圍內100個智能垃圾箱為例，研究基于智能垃圾箱回收閾值的回收路徑優化問題。為了提高回收效率，提高智能回收服務水平，回收公司A需要預先設置合理的回收閾值o，并運用PSO粒子群算法進行合理的車輛調度。根據已有文獻[5，6]與多次實驗計算基礎上，本文的算法參數設置為：種群規模popsize=100，算法最大迭代次數i_max=200，回收閾值o=80%，智能垃圾箱容量mj=50kg，回收車輛容量qv=500kg，單位距離油價fv=0.8元，回收公司處理能力Q=10000kg，單位時間懲罰成本λe=15，λd=20，車輛租賃成本kv=100元，車輛維修成本元δv=50，回收品固定處理成本ρ=1000元，回收品變動處理成本σ=0.15元。以回收公司運營成本最小化為目標，結合智能垃圾箱回收閾值對車輛路徑進行優化，基于智能垃圾箱回收閾值的回收路徑優化前后各項指標對比如表2所示。

表2 基于智能垃圾箱回收閾值的回收路徑優化對比

由表可知，經過回收路徑優化后，回收公司運營成本有效降低了33.80%，車輛使用數降低了3輛。其中，違反時間窗懲罰成本降低了78.39%，車輛租賃成本與維修成本均降低了37.50%，運輸成本降低了36.94%。此外，為了進一步確定合理的回收閾值，本文探討了不同回收閾值下滿足回收條件的垃圾箱數量、回收品數量、車輛使用數與回收公司運營成本的變化情況，如表3所示。

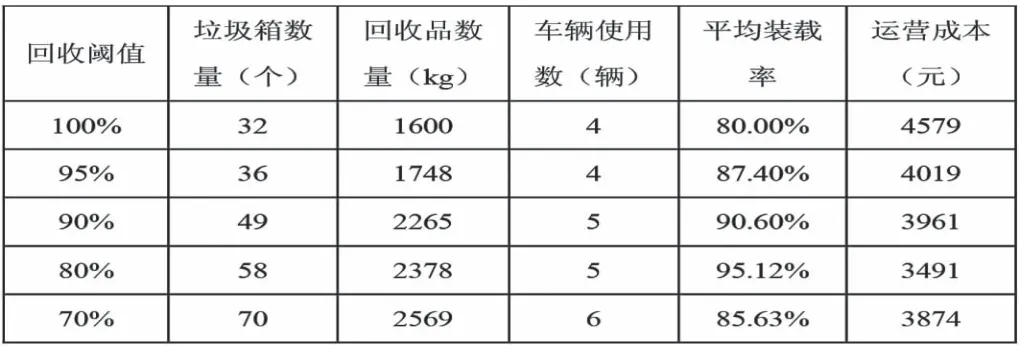
表3 不同回收閾值下指標對比

由表可知，隨著回收閾值由100%降低到70%，需要服務的智能垃圾箱數量逐漸增多，有32個增加值70個，收集到的回收品數量由1600kg增加值2569kg，回收車輛使用數由4輛增加值6輛。此外，本文通過對比不同回收閾值下回收車輛的平均裝載率來確定最優的回收閾值。不同回收閾值下回收車輛的平均裝載率、車輛使用數與回收公司運營成本的對比圖如圖2所示。

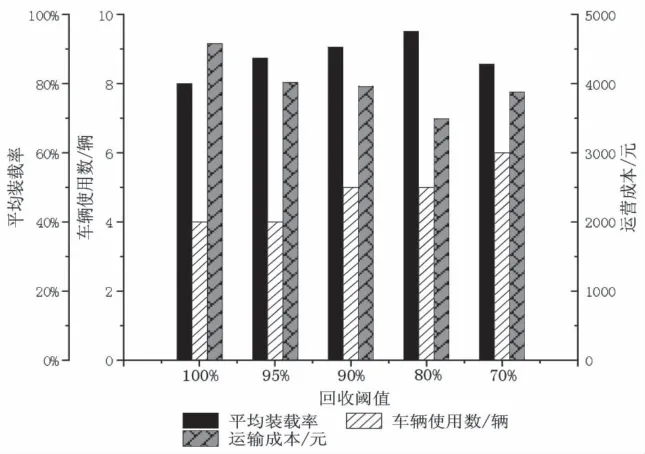
圖2 不同回收閾值下指標對比

由表3和圖2可知，當回收閾值為80%時，車輛平均裝載率達到最大值，為90.60%，回收公司運營成本達到了最小值，為3491元；相比于回收閾值分別為100%、95%、90%和70%的場景，運營成本分別降低了23.76%、13.14%、11.87%和9.87%。綜上所述，回收公司預先確定回收閾值為80%時，可以獲得最低的運營成本。

5.結論

本文研究了基于智能垃圾箱回收閾值的回收車輛路徑問題，考慮了當回收公司預先確定合理的回收閾值進行回收服務時運營成本的變化情況，建立了回收公司運營成本最小化的成本模型，并運用PSO粒子群算法進行求解。以智能回收公司A為例，對其服務范圍內智能垃圾箱的回收路徑進行優化，并對模型與算法的有效性進行了驗證。研究結果表明，經過回收路徑優化后，回收公司運營成本有效降低了33.80%，車輛使用數降低了3輛。不同回收閾值下優化目標的對比結果表明，相比與回收閾值為100%、95%、90%和70%的場景，回收公司預先確定80%為回收閾值時，車輛平均裝載率最高，為90.60%，回收公司運營成本最低，為3491元。本文豐富了智能回收優化調度理論，為研究逆向物流車輛路徑問題提供了新的研究思路，進而為智慧城市回收網絡優化建設提供了方法借鑒。

引用出處

[1]林晶晶,毛雅婧,林宗平.“互聯網+再生資源回收”模式推進機制的三方演化博弈研究[J].生態經濟,2022,38(03):202-209.

[2]丁夢思,王琰,潘可可,陳學進,李桂榮.智能識別分類垃圾箱的認識與設計[J].科技創新與應用,2022,12(14):78-81.

[3]Hannan,M.A.,Akhtar,M.,Begum,R.A.,et al.Capacitated vehicle-routing problem model for scheduled solid waste collection and route optimization using PSO algorithm[J].Waste Management,2018,71:31-41.

[4]楊景明,穆曉偉,車海軍,呼子宇,侯宇浩.多策略改進的多目標粒子群優化算法[J].控制與決策,2017,32(03):435-442.

[5]卿東升,鄧巧玲,李建軍,劉帥,劉鑫,曾素平.基于粒子群算法的滿載需求可拆分車輛路徑規劃[J].控制與決策,2021,36(06):1397-1406.

[6]郭森,秦貴和,張晉東,于赫,盧政宇,于佳欣.多目標車輛路徑問題的粒子群優化算法研究[J].西安交通大學學報,2016,50(09):97-104.