基于置信熵差的沖突證據融合方法

許石君，侯 毅，鄧新蒲，陳沛鉑，周石琳

（國防科技大學 電子科學學院，長沙410000 ）

0 引言

Dempster -Shafer（D -S）證據理論是由Dempster［1］和他的學生Shafer［2］共同提出的理論，能夠在無先驗知識的條件下，有效處理由隨機性和模糊性帶來的不確定性，已被廣泛應用于目標識別、故障診斷、智能決策和風險評估等領域。

在D-S 證據理論的應用發展中，Zadeh［3］于1986 年指出：Dempster 組合規則的使用在證據高度沖突時會失效。針對以上問題，研究者給出了許多改進的方法，其中使用加權平均的方法對原始證據進行修正后再使用Dempster 組合規則進行融合，能夠較好地保留Dempster 組合規則的良好數學性能—交換律和結合律。

然而，如何合理地確定證據的權重是一個值得研究的問題。Liu［4］提出了一種新的權重因子估計方法，利用基于概率變換的距離和沖突系數來表征相異性，距離代表證據之間的差異，而沖突系數則揭示了兩個基本概率賦值函數強烈支持某假設的分歧程度。相異性的兩個方面在某種意義上是互補的，兩個方面的結合被用作相異性的度量，此度量值便是各個證據的權重值；Xiao［5］將Jousselme 距離推廣到復雜的證據距離，以度量復雜的證據沖突，并將其作為加權因子對原始證據進行修正，以獲得最后的融合結果；Mi［6］提出了基于非沖突元素集的證據沖突處理方法，先利用證據間的相關系數獲得加權平均值，加權平均得到新證據，再通過非沖突元素集判斷后進行折扣計算，以獲得最終的融合結果；Xiao［7］提出了一種基于相似度和置信熵的方法，首先根據基本概率賦值的修正余弦相似性，計算證據的可信度及其相應的全局可信度；其次，根據證據的全局可信度，將原始證據分為可靠證據和不可靠證據兩類；最后，為了加強可靠證據的積極效應，減輕不可靠證據的負面影響，利用鄧熵函數來衡量不同類型證據的信息量，以得到證據權重并修改證據源；An［8］在相似性度量模型中引入模糊推理機制，通過計算模糊貼進度和相關系數來度量證據之間的沖突程度，在此基礎上利用置信熵來計算證據的不確定性，從而得到證據的可信度，并利用量化信息量對每個可信度進行修正，獲得最終的證據權重；Tao［9］提出基于置信熵和誘導有序加權平均算子的算法，同時考慮了證據的不確定性和可靠性，首先計算出各個證據的置信熵和可信度；其次，對各個證據的置信熵從高到低進行排序，基于有序加權平均算子產生有序加權平均對，再利用正則遞增單調函數計算出順序權值，加權平均后的新證據通過融合后得到最終結果；Yan［10］提出基于改進置信熵的加權平均方法，利用改進置信熵度量各個證據的不確定值，以此作為證據的支持度，從而獲得各個證據的權重，并對原始證據進行加權修正，得到加權平均證據，以實現沖突證據的有效融合。雖然，Yan 方法在大多數情況下，能夠較好地處理沖突證據，但該方法是通過改進的置信熵度量整個證據的不確定性值，從全局的角度和不確定性的角度衡量證據之間的差異，并直接將整個證據的置信熵值作為證據支持度，從而確定證據的權重，當沖突證據的置信熵值等于或者大于正常證據時，系統將賦予沖突證據與正常證據相同甚至更大的權重值，導致沖突得不到有效處理。

為此，本文提出基于置信熵差的沖突證據融合方法，利用證據內對應焦元的鄧熵值差度量證據之間的差異，從而合理地確定各個證據的權重值；從局部的不確定性的角度度量證據之間的差異，從而有效克服了現有基于置信熵的方法存在的不足，并通過算例證明了該方法的有效性和優越性。

1 理論知識

定義1［11］識別框架。若Θ ＝｛F1，F2，…，FN｝是由N個兩兩互斥元素構成的有限的完備集合，則稱Θ為識別框架（Frame Of Discernment，FOD）。Fi稱作識別框架的一個元素或事件。由Θ中的所有子集或命題組成的集合稱為Θ的冪集，記為2Θ，可表示為

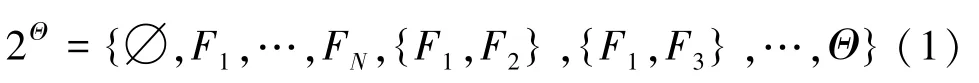
識別框架內的元素是有限可窮舉的，且相互之間不相容。直觀來說，識別框架就是所識別判斷的對象的全體集合，將抽象的邏輯概念轉化成直觀的集合論概念，進而把各個元素之間的邏輯運算轉化為集合論運算。

定義2［1］組合規則。設m1和m2為兩組基本概率賦值，對應的焦元分別為A1，A2，…，An和B1，B2，…，Bm，用m表示組合后的證據，則Dempster 組合規則表示為

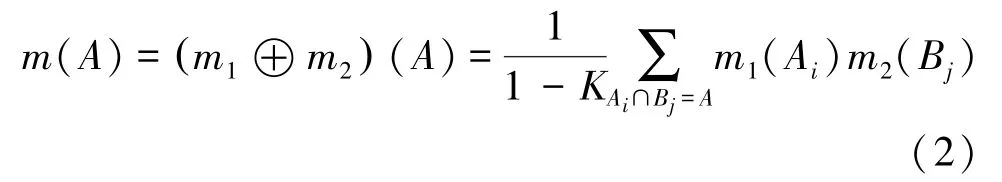
其中，K為沖突系數，表示為（2），式（2），m表示m1和m2的正交和，記為符號⊕。

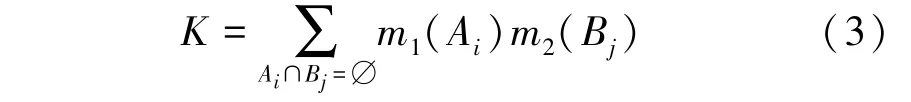
當組合多個證據時，其表達為：

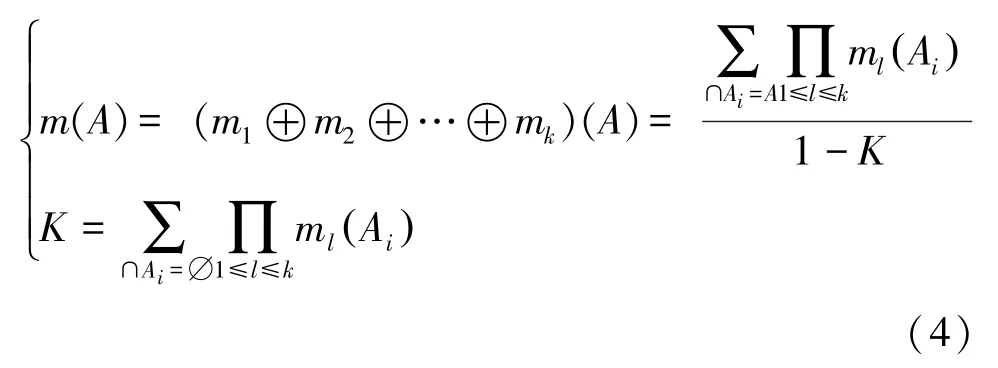
定義3加權平均證據。假設m1，m2，…，mn是從不同的數據源收集到的證據，而w1，w2，…，wn是證據對應的權重，利用權重對原始證據進行修改，得到加權平均證據，表示為（5）

定義4［12］鄧熵。鄧熵是香農熵的推廣，其定義如式（6）

定義5Yan 提出的改進置信熵，通過引入信任函數來擴展不確定性的度量，是在鄧熵的基礎上的拓展與改進，其定義為

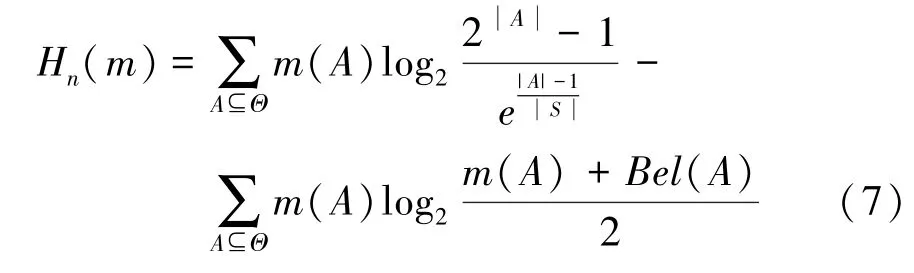
2 基于置信熵差的沖突證據融合方法

2.1 置信熵差

鄧熵是一種改進的置信熵，作為香農熵的推廣，鄧熵是一種有效的測量不確定信息的數學工具。本文在鄧熵的基礎上，提出利用置信熵差度量證據之間的差異。

定義6假設A1，A2，…，Ak是證據mi和mj的焦元，那么證據mi和mj之間的置信熵差表示為

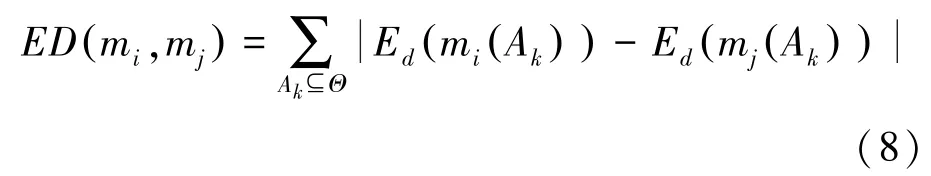
其中，Ed(mi(Ak)) 是焦元Ak的置信熵值。

2.2 證據權重的確定

假設識別框架中有n個證據。

第一步，利用鄧熵式（7）計算焦元置信熵；

第二步，構造置信熵差矩陣，式（9）；

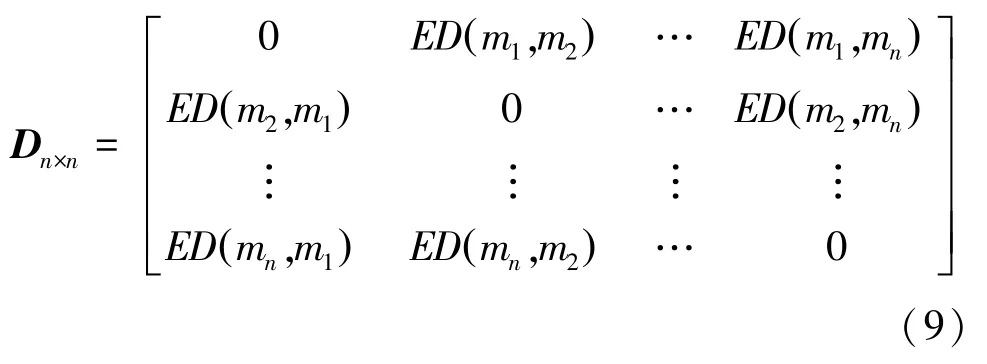
第三步，利用式（10）計算證據體的支持度；

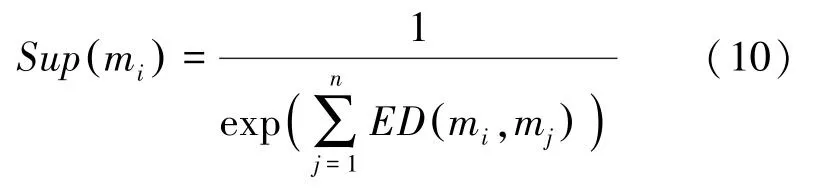
然而，基于置信熵的方法的證據體支持度是由式（11）計算獲得，其值等于置信熵本身；

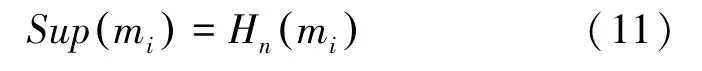
第四步，利用式（12）獲得證據權重。

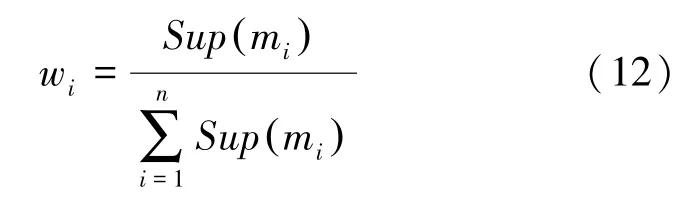
3 數值算例

通過置信熵差度量證據之間的差異以獲得證據權重，對原始證據加權平均得到加權平均證據，利用Dempster 組合規則對加權平均證據進行融合。

3.1 反例1

假設辨識框架Θ ＝{A，B，C}，系統收集到5 個證據，各證據的基本概率賦值（basic probability assignment，BPA）如下：

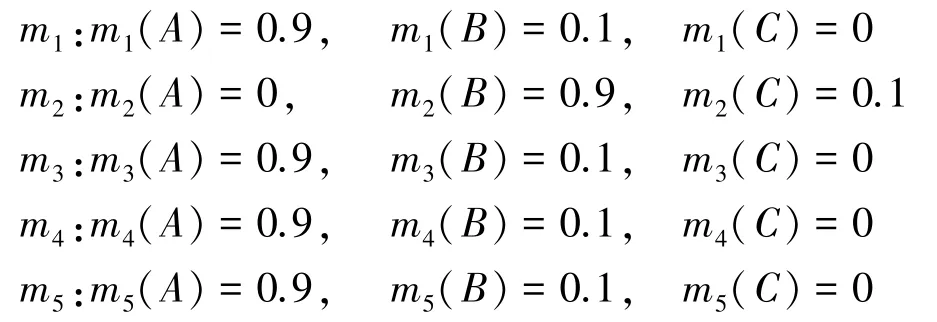
顯然，證據m2與其它證據高度沖突，在加權平均過程中應當得到更小的權重。利用基于置信熵的方法計算各個證據的支持度。

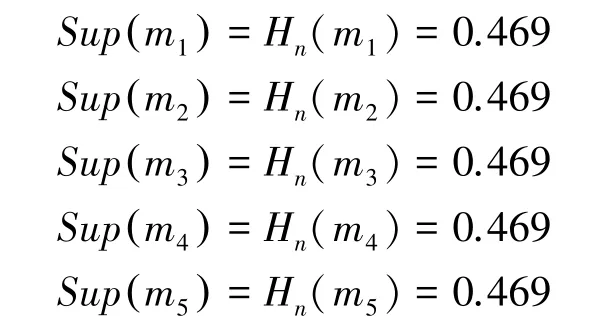
根據式（12）獲得各個證據的權重，見表1。

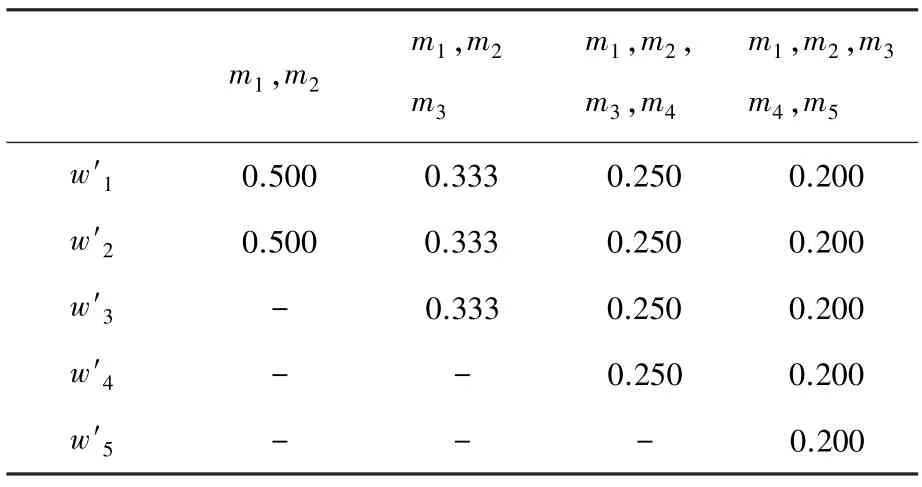
表1 獲得各證據權重值Tab.1 Weight of evidences for Yan’s method

計算各個證據的支持度（以融合前3 個證據為例）。

證據內各焦元的鄧熵值為：

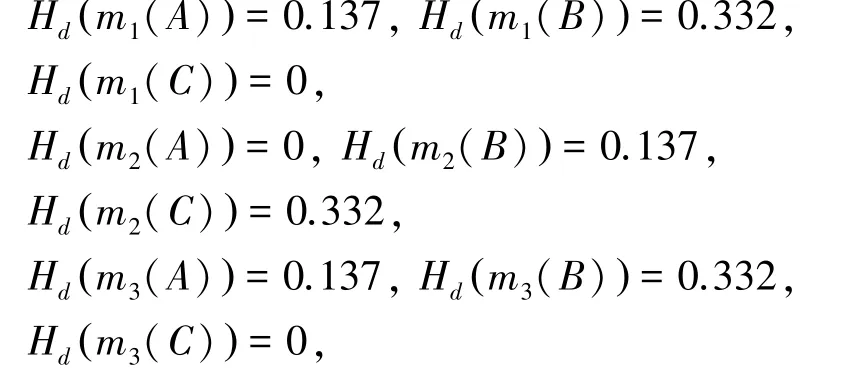
利用式（8）計算各證據之間的置信熵差：（直接給結果）

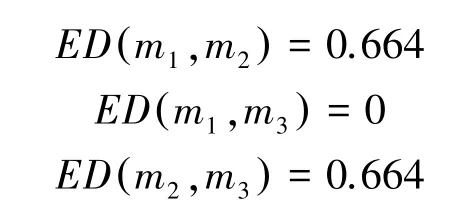
因而，可構建證據置信熵差矩陣D3×3：

利用式（11）計算各證據體的支持度。

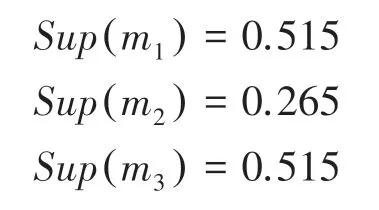
利用式（12）獲得證據權重。

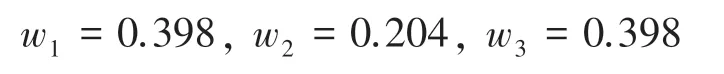
各證據的權重值，見表2，第二個證據權重值的對比如圖1 所示。

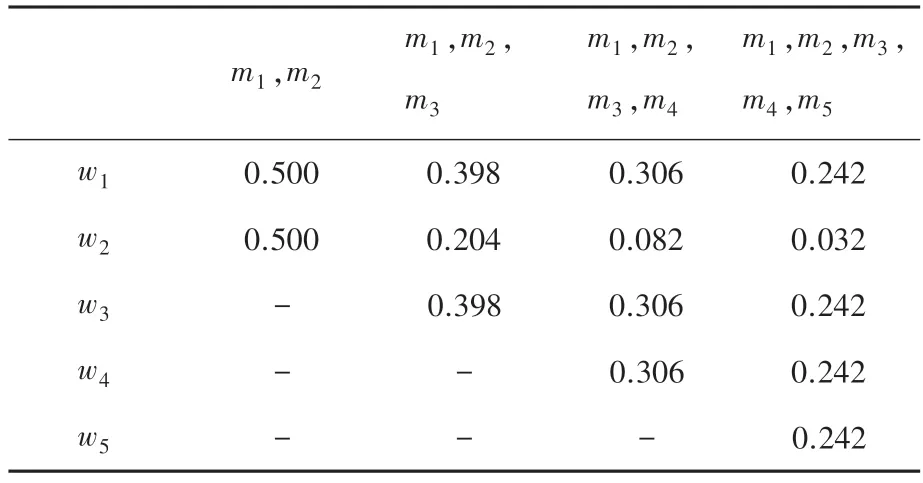
表2 本文方法的各證據權重值Tab.2 Weight of evidences for the proposed method

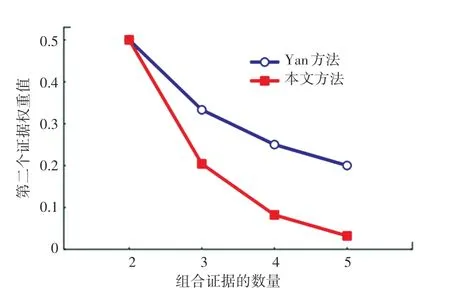
圖1 第二個證據權重值對比Fig.1 Comparison of the weights for the second evidence

由表1 可知，5 個證據的置信熵是相等的，將沖突證據和正常證據都賦予了相同的權重，導致后續融合過程中沖突證據無法得到有效處理。根據表2和圖1 可知，本文提出的方法賦予沖突證據以更小的權重值，能夠很好地區分正常證據與沖突證據。此外，隨著正常證據的增加，沖突證據的權重值下降明顯，使得正常證據的作用得到了最大程度的發揮，沖突證據受到了最大限度的抑制。

3.2 反例2

假設辨識框架Θ ＝{A，B，C}，系統收集到5 個證據，各證據的BPA為：

m1：m1（A）＝0.9，m1（B）＝0，m1（C）＝0.1

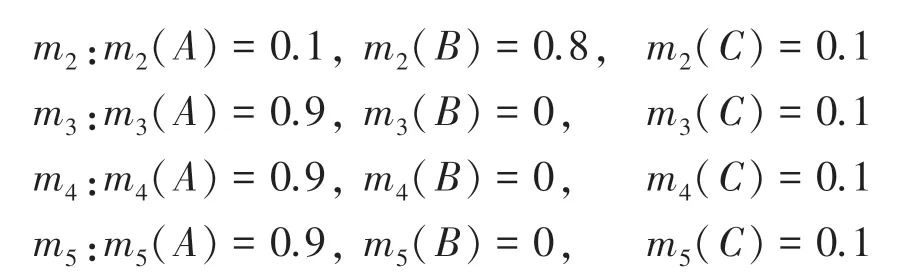
顯然，證據m2與其它證據高度沖突，在加權平均過程中應當得到更小的權重值。利用Han 方法和本文方法得到各個證據的權重值見表3、表4 和圖2 所示。

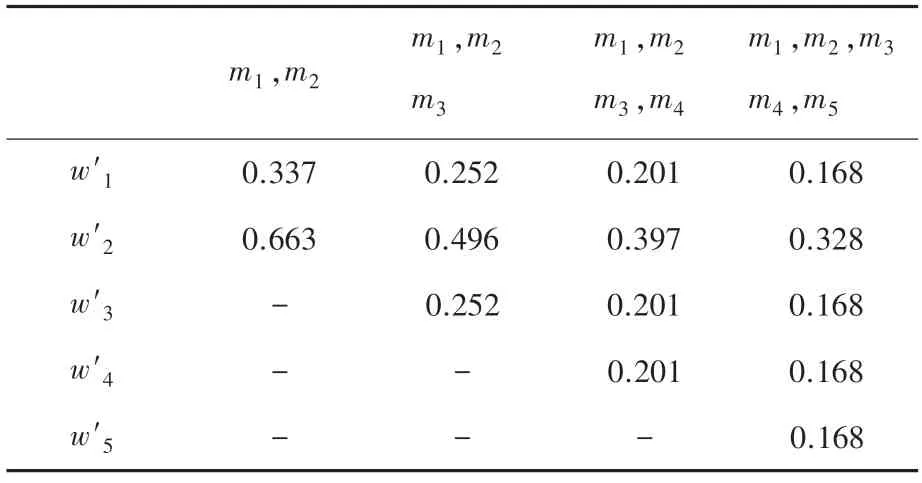
表3 Yan 方法獲得各證據權重值Tab.3 Weight of evidences for Yan’s method

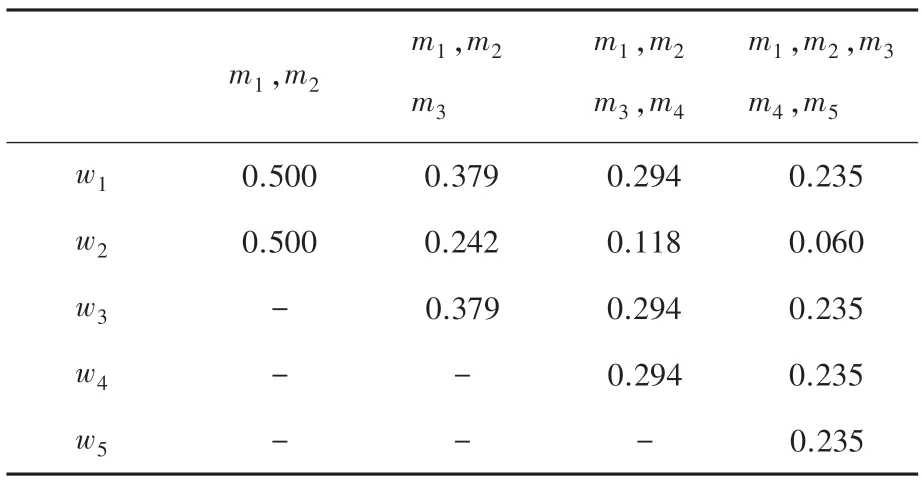
表4 本文方法的各證據權重值Tab.4 Weight of evidences for the proposed method

圖2 第二個證據的融合結果對比Fig.2 Comparison of combination result for the second evidence

根據式（7）可得，沖突證據的置信熵值為0.921大于正常證據的置信熵值0.468，見表3，采用Yan方法的沖突證據權重值反而大于正常證據權重值，即使正常證據個數在增加，但沖突證據權重依然大于正常證據，顯然與事實相違背。根據表4 和圖3可知，本文提出的方法能夠合理地處理沖突證據，賦予沖突證據以更小的權重值，并始終比Yan 方法的權重值更小。此外，隨著正常證據個數的增加，沖突證據的權重值始終保持下降的趨勢，并小于正常證據的權重值，一定程度上減小了沖突證據對后續融合的負面影響。從反例1 和反例2 的對比結果可知，無論沖突證據的置信熵值大于還是等于正常證據，本文方法都能較好地處理沖突證據并賦予一個較為合理的權重值，其有效性得到充分證明。

3.3 識別應用

在多目標識別系統中，A、B和C表示3 種不同的目標，目前共有5 個不同類型的傳感器，各傳感器數據的基本概率賦值如下。顯然，證據m2與其它證據高度沖突，目標A將獲得最高的可信度。

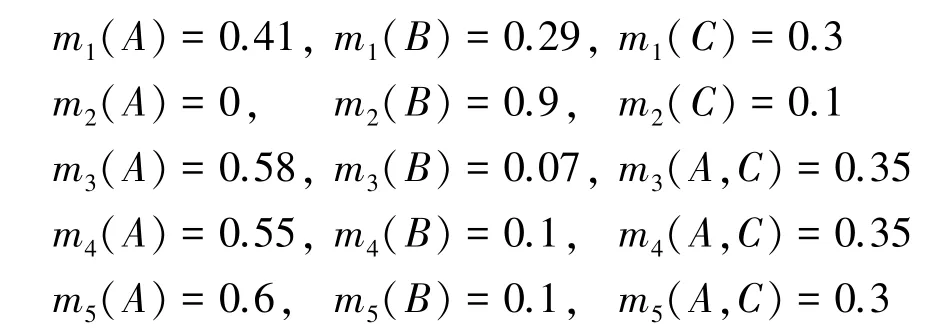
第一步，計算各證據內各焦元的鄧熵值；

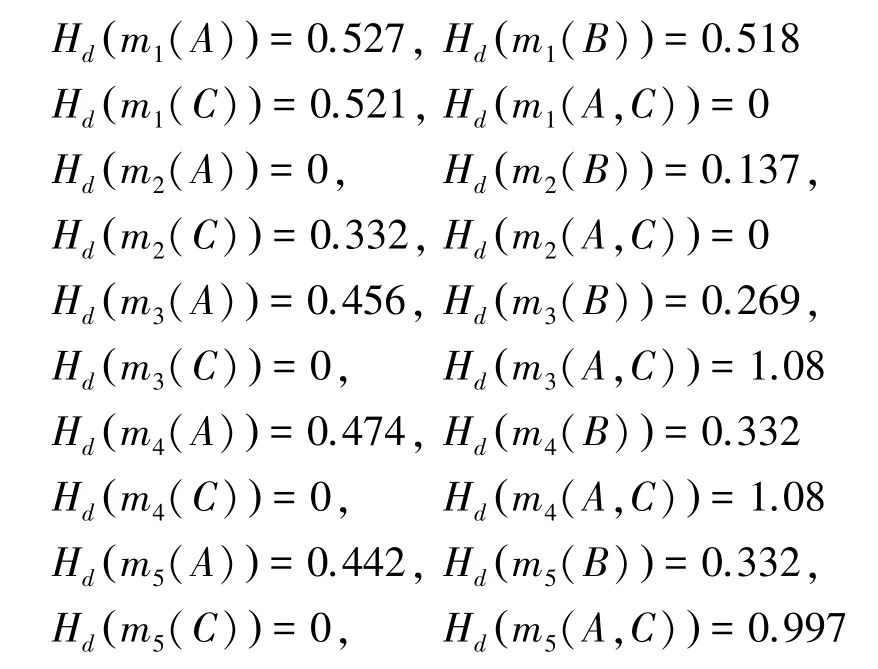
第二步，利用式（10）計算各證據之間的置信熵差；

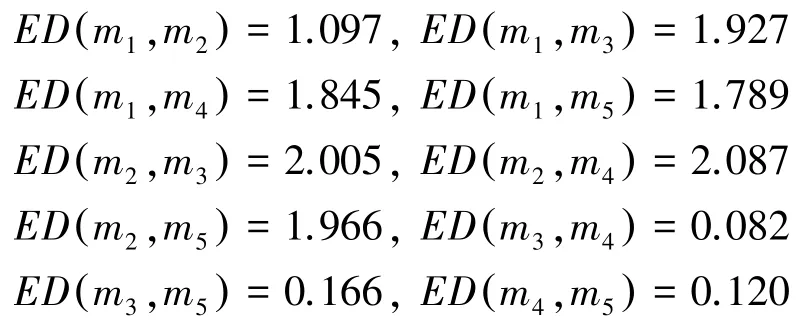
構建證據置信熵差矩陣D5×5；

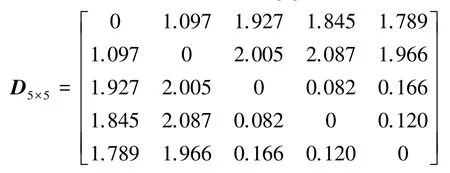
第三步，利用式（11）計算各證據體的支持度；

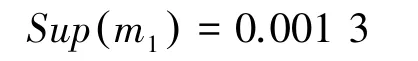
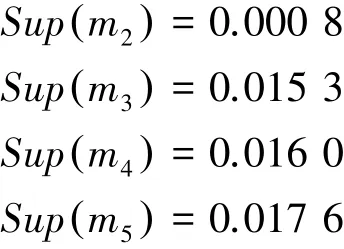
第四步，利用式（13）獲得證據權重；

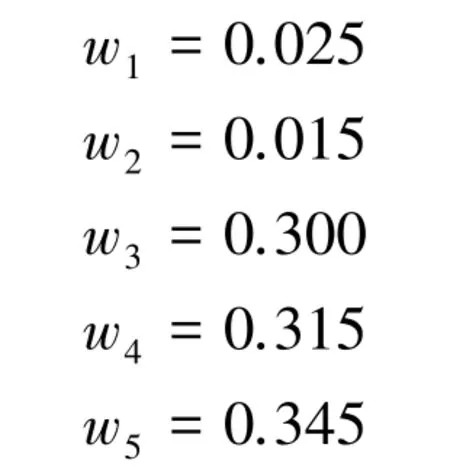
第五步，利用式（14）得到修正后的加權平均證據；

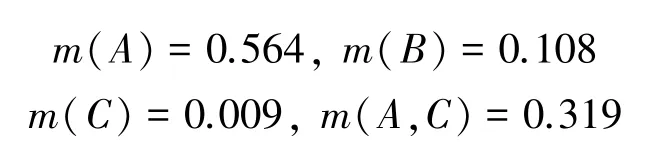
第六步，利用Dempster 組合規則，融合修正后的加權平均證據4 次，得到最終融合結果。

為驗證本文所提方法的有效性和合理性，分別應用Dempster 方 法、Murphy 方 法［13］、Deng 方法［14］、Yan 方法對應用實例中的證據進行融合，各方法的融合結果見表5 和圖3 所示，m(A) 的融合結果對比如圖4 所示。

圖3 融合5 個證據后的結果對比Fig.3 Comparison of results after combination of five evidences

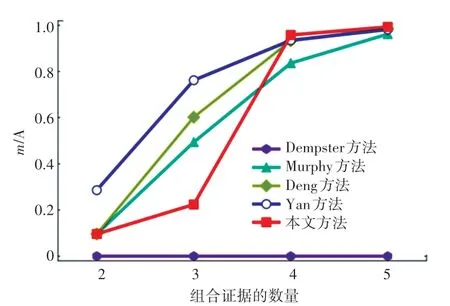
圖4 m（A）的融合結果對比Fig.4 Comparison of m（A）′ combination result

由于證據m2中類別A的基本概率賦值為0，無論支持類別A的證據有多少個，通過Dempster 組合規則融合后，m(A) 的值始終為0，出現“一票否決”的現象，表明經典的Dempster 組合規則在融合高度沖突證據時會得到違背常理的結果。Murphy 方法能夠得到合理的融合結果，但該方法只是對證據進行簡單的加權平均，沒有考慮影響證據權重的其它因素，因而最終融合結果中，正確類別的可信度不是最高。

雖然Deng 方法和Yan 方法在Murphy 方法的基礎上獲得了更高的正確類別可信度，并在整體收斂速度上相較本文方法有一定的優勢，但從證據不確定性的角度可以得到合理的解釋。根據表5 計算結果可知，由于m2置信熵值（0.468）最小，即不確定性程度最低，證據信息的可信度程度高。本文方法在融合m1、m2以及m1、m2、m3時，并沒有過早地否定m2，而是當正常證據m4和m5加入后，在已經確認為沖突證據的情況下，開始抑制沖突證據對后續融合的負面影響，賦予證據m2以更低的權重值，因而在融合4 個或5 個證據時，本文方法的收斂速度最快，獲得了正確類別A的最高置信度0.993，充分說明了本文方法的優越性。

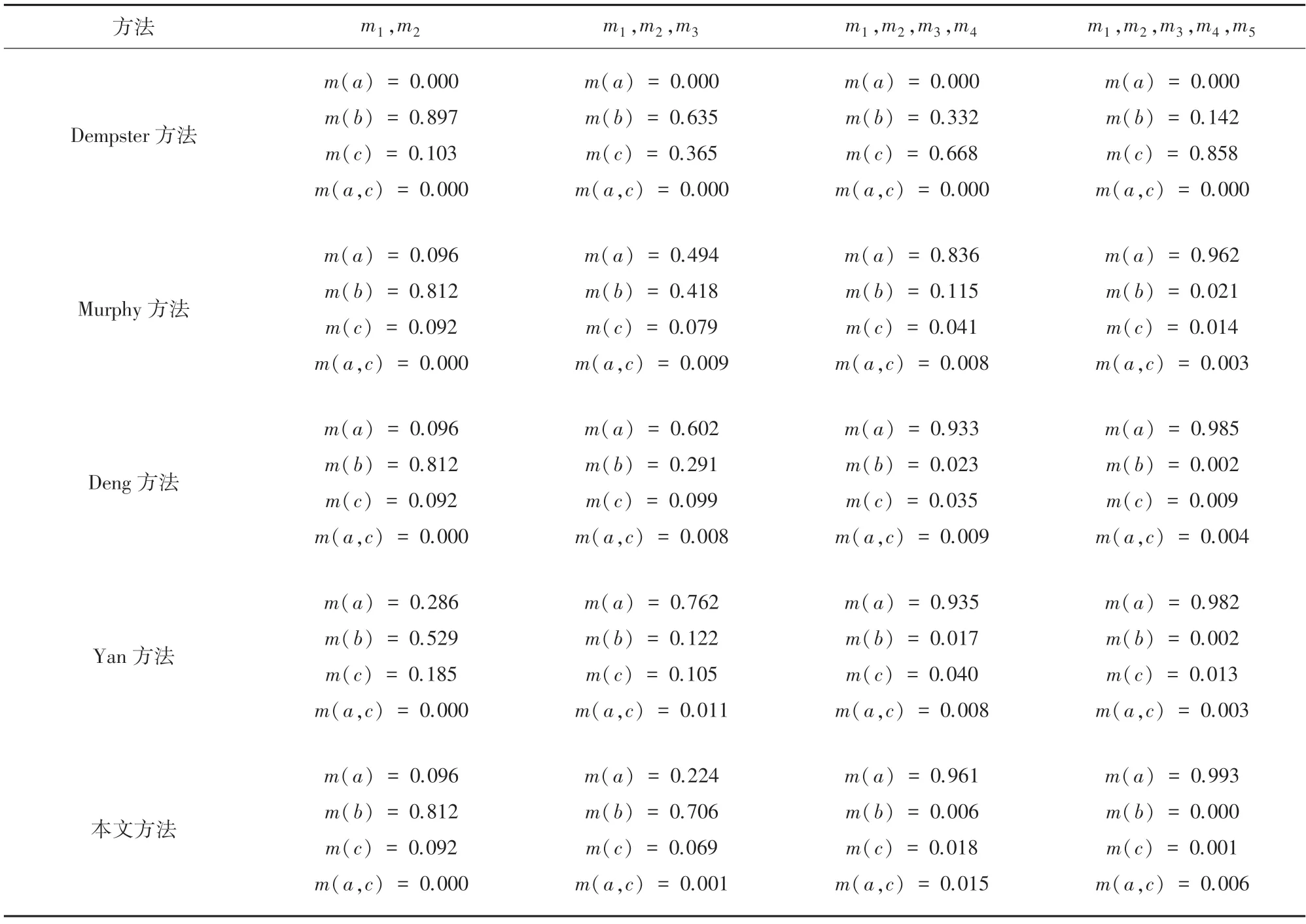
表5 不同沖突證據融合方法的融合結果Tab.5 Combination results of different conflict evidence combination methods

4 結束語

針對現有基于置信熵的加權平均方法，沖突證據置信熵值大于或等于正常證據時，出現的證據權重確定不合理的問題，本文提出了基于置信熵差的沖突證據融合方法。該方法利用證據內對應焦元的鄧熵值差度量證據之間的差異，獲得各證據的支持度，從而確定各個證據的權重值，相比于只簡單地利用整個證據的置信熵值確定證據權重的方法，能夠從局部的不確定性的角度衡量各證據可靠性，使得證據權重的確定更加客觀、準確和合理。算例結果表明，基于置信熵差的沖突證據融合方法，證據權重確定更加符合人的客觀認識，融合結果的正確目標可信度最高。