在加熱階段滾塑模具內表面傳熱系數的兩種研究方法

劉學軍

（北京工商大學人工智能學院，北京100048）

0 前言

滾塑工藝的主要缺點是在加熱階段的能耗比較大［1］，早期對滾塑模具是采用明火直燒的加熱方式，但后來出于節能環保及安全方面的考慮，大部分滾塑模具采用在烘箱內通過熱空氣循環對流的方式來進行加熱。但由于烘箱的壁面和門、泄壓孔等都會向環境散熱，實際上烘箱加熱方式的能量利用率仍然很低［2］。為了進一步降低能耗，近些年來一些研究者提出了對模具采用油加熱和電加熱的方式［3?4］。本文所研究的滾塑模具是一個繞雙軸轉動的電加熱鋁制模具，嵌在該模具外表面上的加熱絲通電加熱模具，用來生產氫氣瓶。所研究的加熱階段是指從通電加熱開始到粉料即將開始熔融的這一過程。

與采用傳統加熱方式的滾塑模具一樣，電加熱模具的內表面也是通過強迫對流換熱將熱量傳給模內的粉料和空氣，同時粉料一邊隨模具翻滾一邊與空氣混合，因此也會從空氣中吸收熱量。無論滾塑工藝采用哪一種加熱方式，模具內表面向模內混合物的傳熱都是一個復雜的氣固兩相流問題。為了強化該傳熱過程，都希望模具內表面的傳熱系數是越大越好。要想定量地評價滾塑模具向模內混合物傳熱的強弱程度，就必須準確地計算出模具內表面上的傳熱系數。另外在建立傳熱理論模型對滾塑工藝進行仿真計算時，模具的內表面傳熱系數通常是作為事先已知的輸入參數，而傳熱系數的準確性直接影響了仿真的精度。因此探索模具內表面傳熱系數的研究方法在滾塑研究中具有重要的理論意義。

以往很少有文獻對模具的內表面傳熱系數進行理論或實驗方面的研究，在用到該傳熱系數時都是按經驗給出一個估計值，并沒有相應的理論或實驗依據。Nugent等［5］測量了一個未裝粉料的鋼制模具的外表面溫度和模內溫度，然后通過傳熱模型得出加熱過程中其內表面傳熱系數是1 W/（m2?K），但未裝料的模具與實際的滾塑模具有本質的差別。在文獻［6］?［9］中采用的模具內表面傳熱系數都是5 W/（m2?K）。Banerjee等［10］認為模具內表面與粉料間的傳熱系數為25 W/（m2?K），與模內空氣間的傳熱系數為 2 W/（m2?K）。Abdullah等［11］認為模具與粉料接觸處的內表面傳熱系數為30 W/（m2?K），與模內空氣接觸處的內表面傳熱系數為0.55 W/（m2?K）。可以看出，現有的研究對模具內表面傳熱系數的取值差異很大。這是因為該傳熱系數的影響因素比較多，也難以預測。它除了與模具的結構形狀、加熱方式和粉料的物性參數有關之外，還很大程度上受模內混合物的流動狀態的影響，而模內混合物的流動狀態又與模具的轉動方式和轉速、模內粉料的體積百分比直接相關。Olinek等［12］通過實驗研究認為當單軸轉動模具的轉速在4～20 r/min的范圍內模內粉料的運動狀態為塌落或者滾落模式，實際商用的滾塑模具的轉速都在這個范圍內。田昊等［13］通過實驗研究了二維回轉圓筒內顆粒流的速度分布及顆粒溫度，并重點研究了滾落的流動模式。雖然回轉圓筒與實際的滾塑模具有一定的差異，但他們的研究結論有助于理解粉料的運動情況影響模內傳熱系數的機理。文獻［14］通過對傳熱模型進行計算來研究一個繞單軸轉動的圓筒形滾塑模具的內表面傳熱系數隨模具轉速的變化規律，但沒有研究該傳熱系數與模內粉料的體積百分比的關系。

本文提出了兩種研究方法來獲得在加熱階段滾塑模具的內表面傳熱系數。第一種方法是實驗與理論相結合的方法，即首先通過實驗測量了在4種情形下電加熱滾塑模具的外表面溫度和模內溫度，然后應用能量守恒原理建立一個描述該加熱階段的傳熱模型，并將實測溫度值的擬合多項式代入該傳熱模型的微分方程式中即可計算出模具的內表面傳熱系數。第二種方法是將繞雙軸轉動的實際模具等效地簡化為一個繞單軸轉動的圓筒形模具，然后通過FLUENT軟件的多相流模塊中的Mixture模型對其進行仿真計算來得出模具的內表面傳熱系數。最后比較了這兩種方法所得的結果，并得出了該傳熱系數隨模內粉料的體積百分比的變化規律。所得結論可為強化電加熱滾塑工藝的模內傳熱過程提供理論依據。

1 模內溫度和模具外表面溫度的實驗結果

本實驗所采用的粉料為線性低密度聚乙烯，其牌號為M3204RUP，粉料的表觀密度為317 kg/m3、真實密度為932 kg/m3、熔點為125 ℃、結晶點為110 ℃、熔體流動速率為4 g/10 min，生產廠家為泰國SCG ICO有限公司。

電加熱絲的最大功率為700 W/m，滾塑機的內、外軸轉速分別設定為11 r/min和1.2 r/min。所采用的滾塑模具如圖1所示，用來測量模具外表面溫度的熱電偶探頭分別安裝在1點和2點的位置，模具外表面上的凹槽用來嵌入電加熱絲。所制造的氫氣瓶的縱向剖面形狀和尺寸如圖2所示，δ為氫氣瓶的設計厚度。本文將在4種情形下測量模具的外表面溫度和模內溫度。這4種情形下的氫氣瓶厚度、模內裝填的粉料質量、粉料在模具內部空間所占的體積百分比如表1所示。

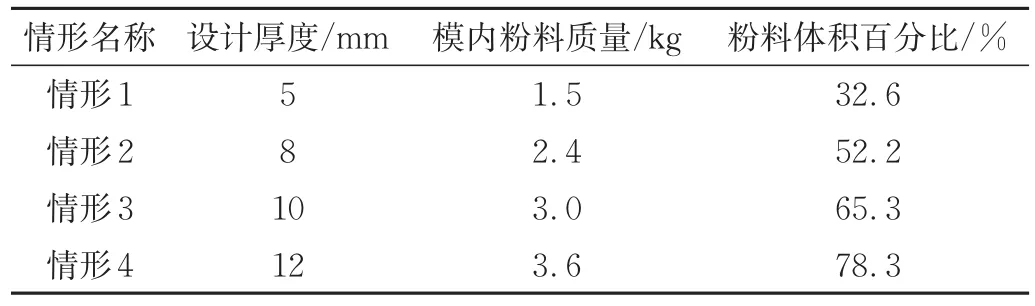
表1 4種實驗情形的描述Tab.1 Description for four kinds of experimental cases

圖1 電加熱的滾塑模具Fig.1 Rotational mold heated by electricity

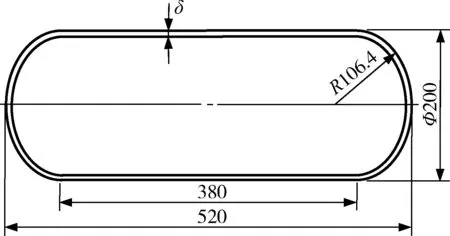
圖2 氫氣瓶的剖面形狀和尺寸Fig.2 Cross section and dimension of the hydrogen tank

圖3表示了在情形1時實測的模內溫度和模具外表面溫度隨時間的變化規律。在該圖中的A點是模具外表面的平均溫度上升到135 ℃時所對應的時刻，這個溫度比本實驗所用粉料的熔點高10 ℃。本文認為從A點開始模內的粉料開始熔融，即從初始時刻到A點所對應的時刻是本文所研究的加熱階段。以往的研究通常認為當模具的外表面溫度升高到粉料的熔點時粉料開始熔融［6?8］。但是由于模具沿厚度方向的導熱熱阻和模具內表面與模內粉料間的對流換熱熱阻都不等于0，因此當模具的外表面溫度剛升到粉料的熔點時，模內粉料的溫度肯定低于其熔點。從圖3可以看出，在A點時刻之前模具外表面上1點和2點間的溫差很小，即模具表面溫度分布的均勻性較好。但從A點時刻開始此二者間的溫差隨時間顯著增大，這個現象說明此時已有粉料變成了熔融的塑料層，且已經覆蓋了部分的模具內表面。這是因為熔融塑料層的流動性比熔融前粉料和空氣的混合物差很多，所以此時模具與模內混合物的對流換熱的強度變得較弱，模具表面的溫度分布也就變得越來越不均勻。因此選擇當模具外表面不同位置處的溫差開始顯著變大的時刻即A點作為粉料開始熔融的時刻是比較合理的。在圖3中B點是模具外表面上的電加熱絲斷電的時刻，即從B點開始模具的外表面溫度開始下降，但由于模具內部積蓄的熱量還會繼續向模內傳遞，因此模內的溫度還會繼續升高一段時間。即模內的最高溫度比模具外表面的最高溫度滯后一段時間。

圖3 在情形1實測的模內溫度和模具外表面溫度隨時間的變化Fig.3 Variation of tested temperature inside the mold and at outer surface of the mold with time in case 1

在圖3中還有一個值得注意的現象是在整個加熱過程的前期，模內的溫度隨時間呈現較大幅度的波動變化，這是因為在本實驗中伸入模具內部的測溫探頭周期性地被塌落或滾落的粉料沖刷。如果把模內的粉料和空氣當成兩相混合物的話，那么隨著模具的運動，在不同的時刻測溫探頭會周期性地遇到不同體積百分比的兩相混合物，當然也包括純空氣和純粉料，從而測量到不同的溫度值。可以認為在圖3中模內溫度的波峰值是當測溫探頭遇到純空氣即模內空氣的體積百分比為100 %、粉料的體積百分比為0的混合物所測得的溫度值；而模內溫度的波谷值是當測溫探頭遇到純粉料即空氣百分比為0、粉料百分比為100 %的混合物所測得的溫度值，在這兩者之間對應的則是模內混合物在其他濃度時的溫度值。在粉料開始熔融后，隨著時間的推移，模內殘留的粉料越來越少，另外這些殘留的粉料與空氣也混合得越來越均勻，因此在整個加熱過程的后期，模內溫度的波動也就變得越來越小。

2 實驗數據的處理

為了便于在之后的傳熱模型中應用上述實測溫度值來計算模具內表面的傳熱系數，需要對這些實驗數據進行處理。首先將圖3中在模具外表面1點和2點處的實測溫度值取其平均值，求得模具外表面的平均溫度，并將該圖中A點以后的溫度曲線截掉，從而得到圖4。在情形1，A點時刻即模具外表面的平均溫度上升到135℃所對應的時刻為171s。

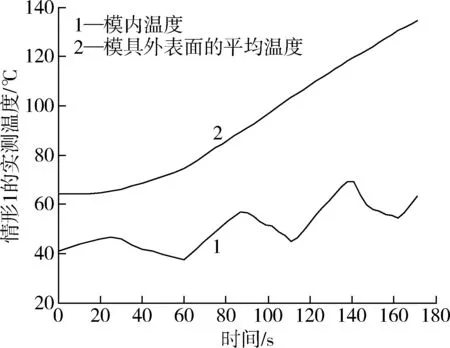
圖4 在情形1的加熱階段實測的模內溫度和模具外表面的平均溫度Fig.4 Temperature inside the mold and average temperature at outer surface of the mold tested for heating phase in case 1

模內粉料和空氣的混合平均溫度應該介于圖4中模內溫度實測值的波峰與波谷之間，即低于純空氣的溫度，又高于純粉料的溫度。如式（1）所示，對模內溫度的實測值采用二階擬合多項式來表示模內混合物的平均溫度隨時間的變化規律。這樣既能保證擬合的精度，同時又能保證擬合所得的溫度值隨時間總是單調上升。

式中 a、b、c——擬合多項式的系數

t——時間，s

Tap——模內混合物的平均溫度，℃

如式（2）所示，對實測的模具外表面平均溫度隨時間的變化規律則采用三次多項式來擬合表示。

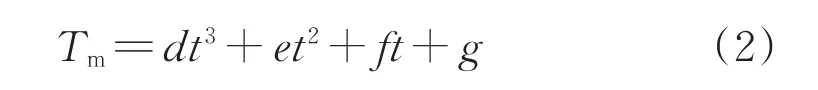
式中 d、e、f、g——擬合多項式的系數

Tm——模具外表面的平均溫度，℃

圖5表示了在情形1～4按式（1）和（2）擬合所得的模內混合物及模具外表面的平均溫度的擬合曲線，模具外表面平均溫度上升到135 ℃所對應的時刻分別為186、162、147 s。擬合多項式中的所有系數由Matlab軟件計算給出，如表2所示。

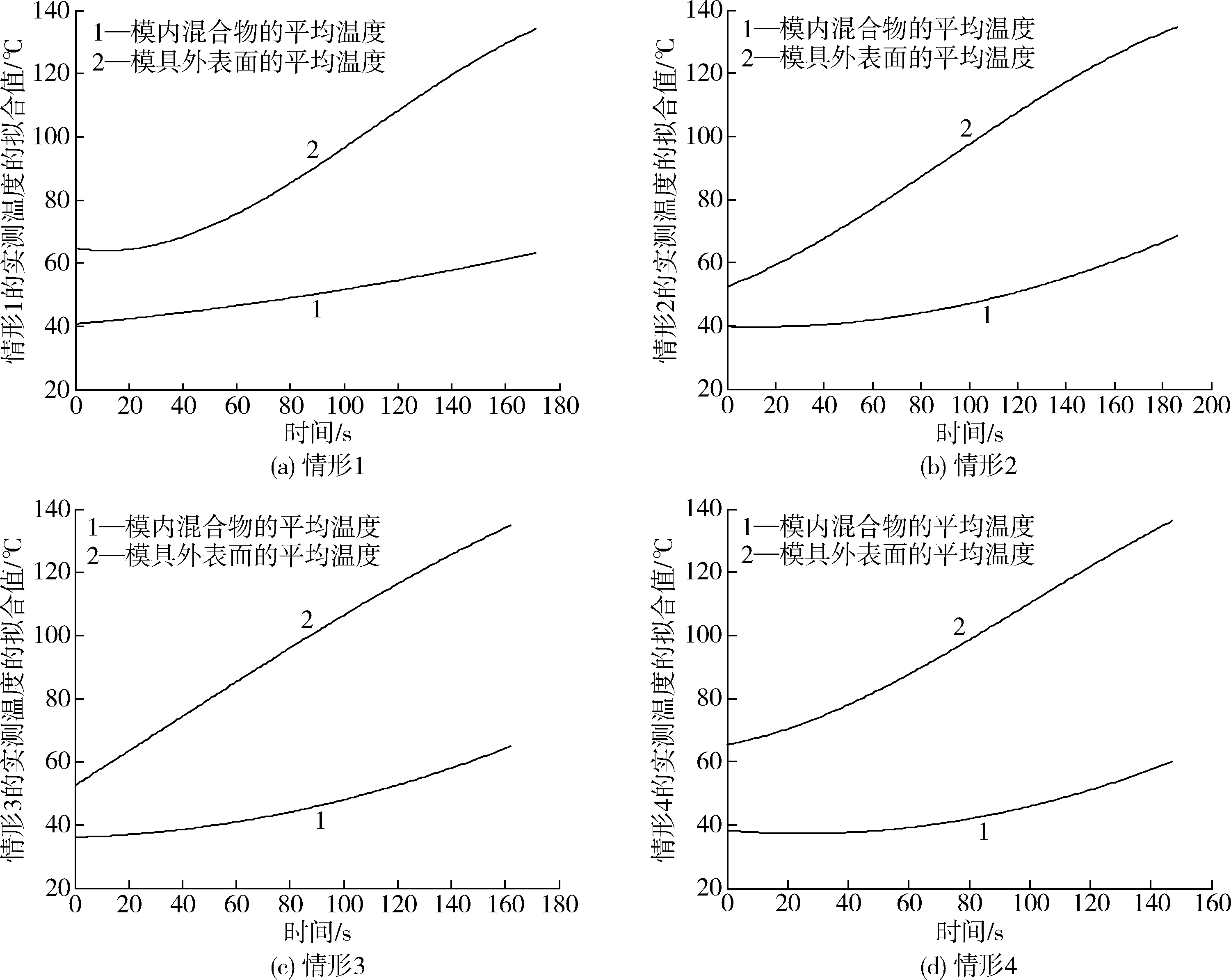
圖5 在情形1～4的加熱階段模內混合物及模具外表面的平均溫度的擬合曲線Fig.5 Fitting curves of average temperature of mixture inside and at outer surface of the mold for heating phase in case 1～4

表2 在4種情形下實測溫度的擬合多項式中的系數Tab.2 Coefficients of fitting polynomials of tested temperature in four cases

3 傳熱模型的建立

3.1 第一種方法的傳熱模型

在第一種方法中，需要建立一個傳熱模型才能將實測的模具和模內溫度轉換為模具內表面的傳熱系數。在建立該模型時，先作出以下兩點假設：（1）、忽略模具沿其壁厚方向的溫度梯度。由于鋁制模具的熱導率比較大，壁厚很薄，因此該假設與實際情況相差不大。（2）、將模內粉料與空氣的混合物當成一個整體來處理，在計算中采用模內粉料與空氣的混合平均溫度，即采用圖5中所示的擬合之后的模內平均溫度。

根據以上假設，模具溫度和模內溫度都只是時間的函數，而與空間位置坐標無關，因此所列出的控制方程為簡單的常微分方程。根據能量守恒原理可知模具內表面與模內混合物的對流換熱量等于模內混合物內能的增量，由此得到本傳熱模型的控制方程（3）。

初始條件為t=0，Tm=Tm0，Tap=Tap0。

式中 Ai——模具內表面的面積，m2

cap——模內混合物的定壓比熱容，J/（kg·K），根據模內空氣和粉料的質量百分比按如式（4）計算所得。

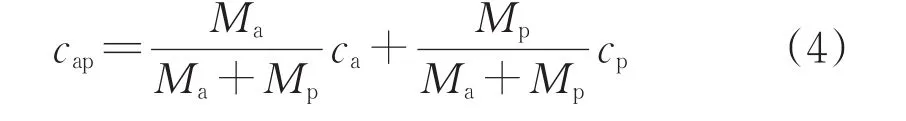
ca——模內空氣的定壓比熱容，J/（kg·K）

cp——模內粉料的定壓比熱容，J/（kg·K）

hi——模具內表面瞬時的傳熱系數，W/（m2·K）

Ma——模內空氣的質量，kg

Mp——模內粉料的質量，kg

t——時間，s

Tap——模內混合物的平均溫度，℃

Tap0——模內混合物的初始溫度，℃

Tm——模具的平均溫度，℃

Tm0——模具初始溫度，℃

參數設置：Ai=0.362 m2，ca=1 005 J/（kg·K）。根據文獻［15］的DSC實驗測得粉料在室溫下其比熱容為1 910.7 J/（kg·K），當粉料溫度高于134 ℃時其比熱容為2 491.7 J/（kg·K），本文采用二者的平均值為cp=2 201.2 J/（kg·K）。在情形1～4中模內粉料的質量Mp如表1所示，模內空氣質量分別為Ma=0.015、0.014、0.013、0.012 kg。

將上述參數及擬合多項式（1）和（2）代入式（3）可以分別計算出在4種情形下模具內表面瞬時的傳熱系數hi。在實際應用中平均的傳熱系數更有意義，因此將瞬時的傳熱系數代入式（5）可計算出在加熱階段模具內表面平均的傳熱系數him，式中的Δt為所研究的加熱階段的時長。以后如不特別提出，本文中模具內表面的傳熱系數指的均是在加熱階段平均的傳熱系數。

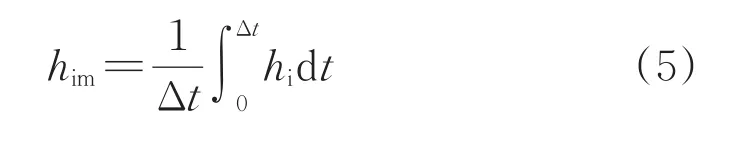
3.2 第二種方法的傳熱模型

采用FLUENT軟件的多相流模塊對模內粉料與空氣的運動和傳熱進行仿真計算，以獲得模具內表面的傳熱系數。就是將模內的空氣當作兩相流中的主相，由于模內粉料的顆粒尺寸非常小，可以近似看成是連續流體，因此將粉料當作是該兩相流中的第二相。粉料流體的黏度系數沒有任何實驗數據可供查詢，也無法由精確的計算公式得出，本文采用式（6）［16］近似計算該黏度系數。

式中 μa——模內空氣的動力黏度，Pa?s

μp——粉料流體的動力黏度，Pa?s

ρa——模內空氣的密度，kg/m3

ρp——粉料的表觀密度，kg/m3

FLUENT軟件的多相流模塊提供了VOF、Mix?ture、Eulerian 3種模型。VOF模型適用于兩相間不混溶的流體，這與模內空氣和粉料的混合運動不相符，故不采用。Eulerian模型在兩相間的阻力定律已知的前提下比Mixture模型的計算結果更準確，但目前滾塑模內粉料與空氣之間相互作用力的規律是未知的，而且Eulerian模型求解的方程數更多，計算量更大，因此本文決定采用較簡單的Mixture模型來仿真求解模具內表面的傳熱系數。

為進一步減小計算量，本文將圖1所示的實際模具簡化為橫截面形狀如圖6所示的一個圓筒，這樣三維問題就簡化為更簡單的二維問題。為保證流動與傳熱的等效性，在簡化時要求模具和模內粉料的質量都保持不變，模具的內徑以及模內粉料的體積百分比也都保持不變。 實際的模具繞雙軸轉動，在對簡化后的二維問題進行仿真時，只考慮圓筒繞軸線以11 r/min轉動的情形，即忽略了實際模具以1.2 r/min繞外軸的轉動。由于繞外軸的轉速很低，因此忽略該轉動對仿真精度的影響應該比較小。

圖6 第二種方法的傳熱模型的示意圖Fig.6 Schematic of heat transfer model of the second method

仿真的區域包括模具本身和模內的粉料和空氣。將圖1所示的模具外表面的電加熱絲等效轉換為圖6所示的圓筒壁的內熱源，該內熱源的強度qv等于實際所用電加熱絲的總發熱功率除以該圓筒的體積，經過計算可得qv=2 047.6 kW/m3。在電加熱絲的總發熱量中，有一部分熱量Qe被用于加熱模具本身和模內的粉料和空氣，另一部分熱量Qc則傳給了外界環境。Qc包括模具外表面以對流換熱方式傳給環境空氣的熱量、以輻射換熱方式傳給環境壁面的熱量以及以導熱方式傳給與其接觸的模架等附件的熱量。如圖6所示，這部分熱量是通過模具的外表面傳熱系數ho來考慮的，也就是說ho是綜合考慮了模具外表面的對流換熱、輻射換熱和導熱的總傳熱系數。在ho的大小已知后，模具的外表面就可以被定義為第三類熱邊界條件。本文按如下方法計算ho，首先按式（7）計算Qe的大小。因為模內空氣的質量很小，因此計算Qe時忽略了空氣的吸熱量。

式中 cm——模具的定壓比熱容，J/（kg·K）

L——粉料的熔融潛熱，J/kg

Mm——模具的質量，kg

Tm——在電加熱絲斷電時模具的溫度，℃

Tp——在電加熱絲斷電時粉料的溫度，℃

Tm0——模具的初始溫度，℃

Tp0——粉料的初始溫度，℃

參數設置：cm= 904 J/（kg·K），L = 180 000 J/kg［6］，Mm=9.46 kg。在情形 1，通過實驗測得 Tm=230.5 ℃、Tm0=64.2 ℃、Tp=179.7 ℃、Tp0=41.1 ℃。另外通過實驗還可測得從加熱過程開始到電加熱絲斷電所花的時間為677 s，在這段時間模具外表面的平均溫度為180.5 ℃，以及扣除電機空轉后的耗電量即實際的加熱電能為4 377.6 kJ。該加熱電能減去由式（7）算出的Qe后得到的就是模具外表面傳給外界環境的總熱量，然后通過牛頓冷卻公式［17］即可算出ho=33 W/（m2?K）。采用同樣的方法可算出在情形2，ho=30.1 W/（m2?K），可見不同情形的ho相差不大，而且模具內表面的傳熱系數受外表面傳熱系數的影響很小，因此在所有情形的仿真計算中統一采用ho=33 W/（m2?K）。

這是一個非穩態的流動與傳熱問題，將模具外表面的對流換熱、模具的導熱與模內空間的多相流換熱耦合在一起，將時間步長設為0.02 s。在每一個時間步長的仿真結束時，記錄模具和模內混合物的平均溫度以及模具內表面上的熱流密度，然后根據牛頓冷卻公式可計算出模具內表面在該瞬時的傳熱系數。當計算所得模具的平均溫度上升到135 ℃時，即認為模內的粉料即將開始熔融，仿真計算結束。然后將所有的瞬時傳熱系數代入式（5）即可計算出模具內表面平均的傳熱系數。

4 計算結果及分析

首先按照這兩種方法分別計算出如表1所示的4種情形下的模具內表面傳熱系數，并進行比較，其計算結果和相對誤差如表3所示。因為第一種方法是以實驗測得的溫度為基礎計算出來的，肯定更接近真實值，因此以第一種方法的結果作為參照值來計算第二種方法在各情形的相對誤差。可以看出在情形1、2、4下第二種方法對模具內表面傳熱系數的計算結果具有較高的精度，但在情形3下誤差較大。

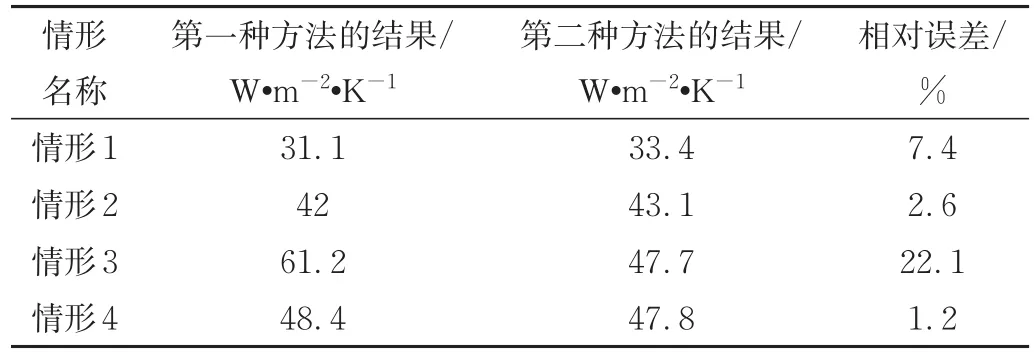
表3 2種方法在4種情形下所得的模具內表面傳熱系數及其相對誤差Tab.3 Heat transfer coefficients at inner surface of the mold and relative errors in four cases by two methods

根據第一種方法在4種情形下所得的結果以及第二種方法在粉料的體積百分比為0～90 %范圍內的仿真結果，可以得到如圖7所示的模具內表面傳熱系數隨模內粉料體積百分比的變化規律。可以看出在粉料體積百分比不超過53 %的時候，兩種方法的結果吻合得很好。這是因為模內的空氣質量很小，模具內表面與模內混合物間的換熱強度主要取決于其與模內粉料間的換熱強度。當模具轉動時，模具內表面與粉料間的換熱強度受2個因素的影響，一個是模內粉料與模具內表面的接觸面積的大小，濃度越高的粉料與模具內表面的接觸面積越大，則模內傳熱系數就越大。另一個因素是模內粉料在自由面或者說是粉料與空氣的分界面上的運動情況。如圖6所示，當粉料處于滾落的運動狀態時，模具的內表面通過摩擦力將溫度較低的粉料從粉料池里帶出到粉料的自由面上，然后沿著切線方向運動，一邊與模內的空氣進行對流換熱，一邊將熱量傳給粉料池里溫度較低的粉料，因此粉料在自由面上的切向運動可以提高模具的內表面傳熱系數。一方面，由于Mixture模型不考慮兩相間的相互作用力，因此采用該模型無法準確地仿真出粉料在自由面上的運動情況，從而導致第二種方法所得的模內傳熱系數低于第一種方法。但當粉料的體積百分比較小時，粉料在自由面上的運動比較弱，因此其對提高模內傳熱系數的作用不是很大，即此時第二種方法的結果比第一種方法的結果低得不是很多。另一方面，仿真模型是一個二維的圓筒，沒有端部效應，而如圖1所示實際的滾塑模具是一個三維實體，其兩端的換熱強度肯定要低于中間的圓筒直段，因此仿真模型的內表面傳熱系數又要高于實際滾塑模具的內表面傳熱系數，即這導致第二種方法的結果又要高于第一種方法。綜合來考慮，這兩個反向的影響大部分相互抵消了，因此在粉料的體積百分比不高的情形，兩種方法的結果吻合得很好，即此時采用第二種方法仿真所得的模具內表面傳熱系數具有足夠的精度。

圖7 模具內表面的傳熱系數隨模內粉料的體積百分比的變化Fig.7 Variation of heat transfer coefficient at inner surface of the mold with volume percentage of powder

當粉料的體積百分比超過53 %，如果繼續增大該體積百分比，粉料在自由面上的運動就會極大地強化粉料與空氣間的對流換熱，從而使得模內傳熱系數快速升高。而第二種方法無法仿真出粉料在自由面上運動的強弱變化，所以此時第二種方法計算出的模內傳熱系數比第一種方法低得較多。但是當粉料的體積百分比超過70 %以后，由于粉料自由面的面積明顯變小，粉料在自由面的運動變弱了很多。所以盡管此時隨著粉料體積百分比的提高，粉料與模具內表面的接觸面積在增大，在一定程度上有強化模內傳熱的趨勢，但還是抵消不了變弱的粉料自由面運動對模內傳熱的削弱作用，因此綜合來看模內傳熱系數開始變小了，從而使得兩種方法的結果趨于接近，即第二種方法的仿真誤差也變小了。

由圖7還可以看出，當粉料的體積百分比達到62 %時，第二種方法所得的模內傳熱系數隨體積百分比的增加而變化很小。圖8是采用第二種方法對該種情形進行仿真所得的模內粉料分別在1 s和100 s時的濃度分布云圖。可以看出由于Mixture模型忽略了兩相間的相互作用力，在較高體積百分比的情形下仿真所得的結果總是粉料較為均勻地分布并充滿整個模內空間，也就是說此時繼續增大體積百分比，均勻濃度的粉料與模具內表面的接觸面積總保持為最大值。而由于Mixture模型無法仿真粉料在自由面的運動情況，因此第二種方法所得的模內傳熱系數只取決于粉料與模具內表面接觸面積的大小，所以此時繼續增大粉料的體積百分比，第二種方法的仿真結果幾乎已經達到了最大值而不再變化。

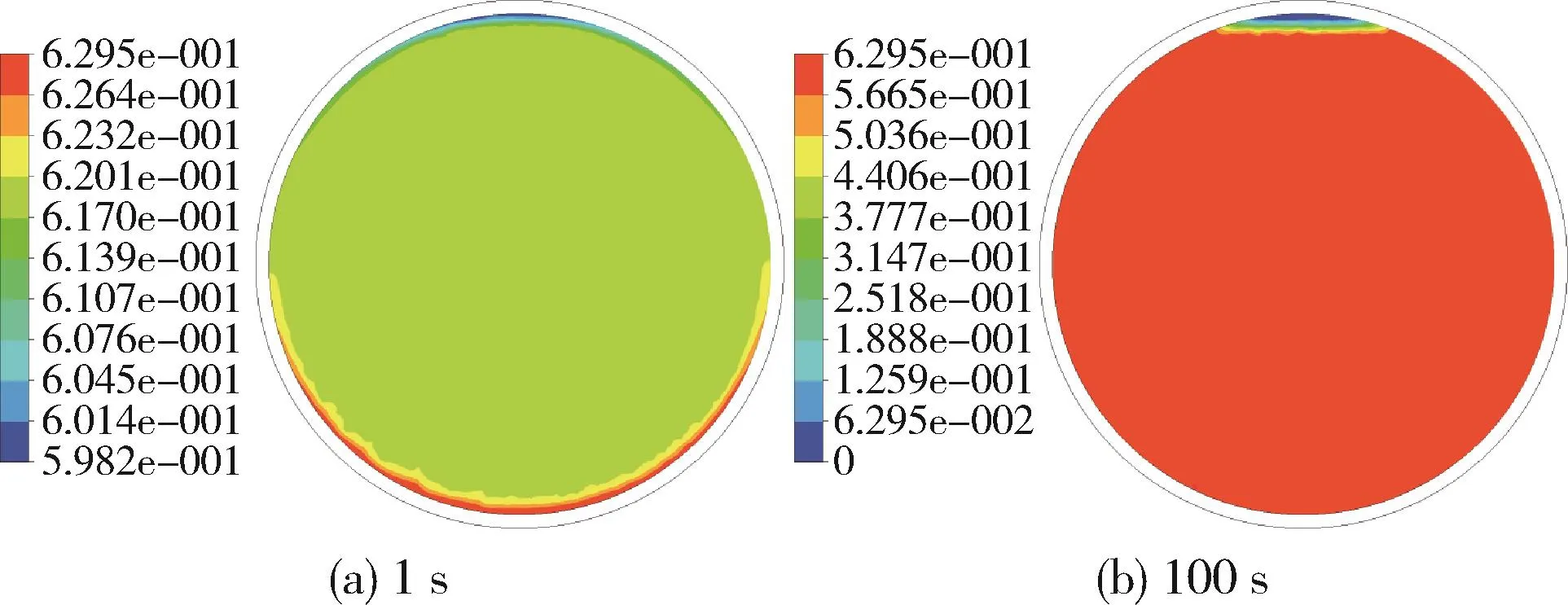
圖8 采用第二種方法對體積百分比為62 %的情形仿真所得的模內粉料濃度在不同時刻的分布情況Fig.8 Distribution of volume fraction of powder inside the mold at different moments by the second method when the volume percentage of the powder is 62 %

綜合兩種方法的結果來看，模具內表面的傳熱系數隨著粉料的體積百分比先是快速增大，然后從10 %開始增大的速率變慢，并在65.3 %時達到了峰值61.2 W/（m2·K），然后隨體積百分比開始減小。另外當粉料的體積百分比不在58 %～74 %的范圍內，由第二種方法仿真所得的模具內表面傳熱系數的相對誤差不超過10 %。考慮到Mixture模型的計算量較小，仿真計算的成本也低于實驗成本，因此在58 %～74 %范圍之外的體積百分比的情形，通過第二種方法來仿真計算模具的內表面傳熱系數在滾塑工藝的研發方面還是具有實際的應用價值。

5 結論

（1）為一個電加熱的滾塑模具在粉料開始熔融前的加熱階段提出了兩種研究模具內表面傳熱系數的方法，第一種方法是通過傳熱模型將實測的模具和模內溫度轉換為該傳熱系數，第二種方法是應用多相流的Mix?ture模型通過FLUENT軟件仿真計算出該傳熱系數；

（2）隨著粉料體積百分比的增加，模具內表面傳熱系數先是快速增大，然后增大的速率變慢，當體積百分比為65.3 %時達到最大值61.2 W/（m2·K），隨后開始減小；

（3）兩種方法所得的模具內表面傳熱系數在情形1、2、4都吻合得很好，當粉料的體積百分比不在58 %～74 %的范圍內，由第二種方法仿真所得的模具內表面傳熱系數的相對誤差不超過10 %。