基于傳質源項的水翼空蝕風險數值預報

鄭恩慧，曹彥濤，程懷玉，季 斌，彭曉星

（1.中國船舶科學研究中心船舶振動噪聲重點實驗室，江蘇無錫 214082；2.武漢大學水利水電學院，武漢 430072）

0 引 言

隨著現代艦船噸位和航速的不斷提升，空化現象也愈發常見。空化往往會顯著增大艦船推進器的振動、噪聲，引起性能下降，嚴重時甚至會直接造成推進器葉片表面材料的剝蝕，引起空蝕，嚴重危害艦船的安全。在推進器的設計過程中，需要在保證推進效率的同時，盡可能減小或避免空蝕的影響。因此需要一個準確客觀的空蝕風險預報方法，以獲取空蝕可能出現的區域和強度，從而為設計方案的優化提供依據。

傳統推進器設計中主要依靠模型涂層試驗來判斷空蝕風險的潛在位置及強度，即通過在模型表面噴涂軟面涂層開展設計工況下的空化試驗，利用涂層剝離區的狀況判斷空蝕風險。Cao 等[1]利用涂層試驗得到了兩種工況下NACA 0009 三維扭曲水翼的空蝕風險區域；Li 等[2]分別對8°攻角NACA 0015 水翼及6.5°攻角NACA 0018-45 水翼進行設計工況下的涂層試驗。但采用試驗方法研究空蝕風險問題通常面臨著試驗周期長、費用高、數據有限等問題。近年來隨著CFD 的不斷發展，空化流動數值模擬技術日趨成熟，其在推進器空化性能的設計評估中得到了廣泛的應用[3-7]。在可靠的空化流場數值模擬結果基礎上，對空蝕風險進行數值預報也成為了可能。目前，研究者們通常以空化流場壓力、蒸汽體積分數等特征參數為依托，通過一些表征參數構建空蝕風險預報的方法。這些方法近年來獲得了較大發展，在空化流場空蝕風險的評估中得到了一定的應用。Dular[8]將蒸汽體積分數的標準差與空蝕風險聯系起來；Nohmi[9]通過觀察數值模擬中的汽泡行為，簡單定義了固壁壓力及蒸汽體積分數的函數來衡量空蝕風險；Ochiai[10]提出了離散泡法，其空蝕風險參數是通過R-P 方程計算微觀汽泡內部的壓力來估計的。

準確可靠的數值模擬結果是開展空蝕風險數值預報的基礎。對于空化流動的數值模擬而言，當前基于均質平衡流模型框架的質量輸運方程空化模型得到了廣泛應用[11-15]。結合改進型RANS、DES或LES等湍流模擬方法[16-20]，可以較好地模擬非定常空化流動的主要特征。

而在空蝕風險表征參數的構建方面，當前存在兩種主要研究思路：一是精細化捕捉空化泡群潰滅特征，利用歐拉-拉格朗日方法精細化捕捉空化潰滅的瞬態載荷特征，但該類方法所需計算資源巨大，當前尚未達到工程實用化的程度[21-25]；另一種思路是拋開復雜的流動細節，基于宏觀流場的參數構建能夠反映空蝕風險特性的表征方法。其中，以勢能假設為基礎的空蝕風險表征參數方法已經獲得較大發展。Patella[26]提出了空泡潰滅后沖擊波的能量傳遞機制；Li[2]提出了基于壓力時間導數的空蝕風險表征參數；Leclercq[27]利用局部勢能變化率結合立體角模型計算了壁面吸收到的輻射能量；Melissar?is[28]假定空泡結構的初始勢能在潰滅前首先轉化為空泡界面處的動能，隨著空泡體積的減小，動能逐漸向空泡中心聚焦，一旦達到潰滅條件，全部能量以壓力波的形式向外釋放，壓力波以投影的方式輻射到壁面上，從而獲得壁面上的空蝕風險區域；Mohammad[29]則直接計算空泡潰滅過程中周圍液體的動能，避免了勢能計算過程中驅動壓強的不確定性問題，并且同時考慮了沖擊波與微射流兩種空蝕作用機制。

上述研究加深了人們對于空蝕風險預報理論與方法的認識，為本文的研究提供了非常有意義的參考。本文基于單泡潰滅模型，分析影響空泡潰滅的因素，在當地壓強大于飽和蒸汽壓及壓強變化率大于某個閾值的前提下，利用傳質源項計算一段時間內由于空泡潰滅引起的壁面上的能量累積，通過為壁面累積能量劃定閾值確定空蝕風險區域的范圍，通過壁面累積能量的大小判定空蝕風險的相對嚴重程度。通過該方法預報NACA 0009三維扭曲水翼的空蝕風險結果，并與試驗結果進行比較，驗證該方法的準確性。

1 水翼空化演化過程數值模擬

1.1 控制方程與大渦模擬方法

本文空化流動計算采用的兩相流模型為mixture 模型。控制方程為連續性方程和動量方程，以張量形式表述如下：

式中，ui是混合物在i方向的速度，p是汽液混合物的壓力。混合物的粘性μ與密度ρ視為蒸汽體積分數αv的函數：

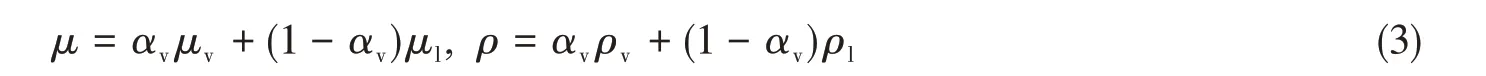
其中，下標v和l分別代表蒸汽相及液體相。

為了能較好地模擬各種湍流尺度及更好地捕捉渦旋結構，本文采用LES 方法模擬湍流。大渦模擬的控制方程為

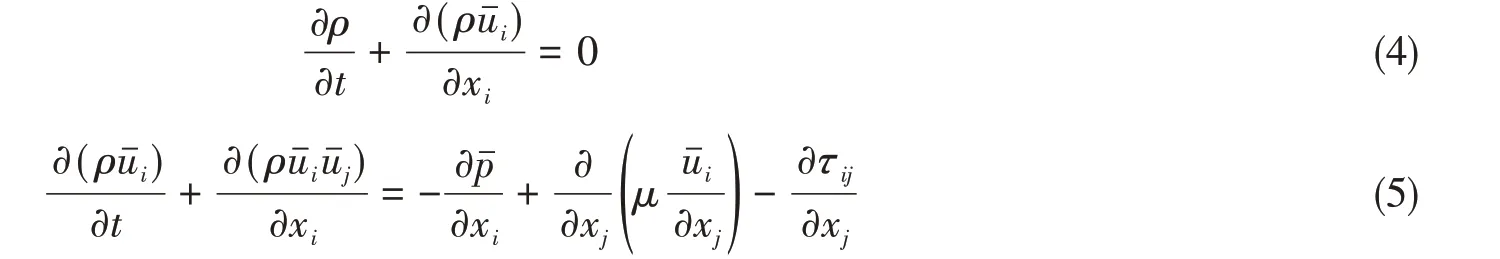
式中，應力項τij用亞格子模型求解。通過WALE 模型模擬亞格子尺度湍流特性。該模型在此類空化流動中已經得到了較為廣泛的應用，取得了令人滿意的預報結果[16,18]

1.2 Schnerr-Sauer空化模型

本文采用的空化模型為Schnerr-Sauer(S-S)空化模型[15]，汽、液兩相間的質量傳輸由蒸汽體積分數輸運方程來控制：

式中：αv表示蒸汽體積分數；ρl為液體密度；ρv為蒸汽密度；m?為汽液兩相間的凈質量輸運源項，又分為蒸汽生成項m?+及凝結項m?-，表征如下：

其中：pd為泡外驅動壓力；pv為飽和蒸汽壓；n為汽泡數密度，本文取n=1×1013。

1.3 計算域及網格劃分

本文采用的水翼模型為三維扭曲水翼，其截面翼型為NACA 0009。弦長為112.5 mm，展長為225 mm，左右對稱，水翼中部攻角為11°，兩端攻角為0°，水翼模型的外形如圖1 所示。圖2 給出了數值模擬中使用的計算域及相應的邊界條件的設置，C為水翼弦長，邊界條件采用速度進口與壓力出口，進口速度為14 m/s，通過調節出口壓力值使空化數等于1.2，空化數定義為

圖1 水翼模型Fig.1 Hydrofoil model

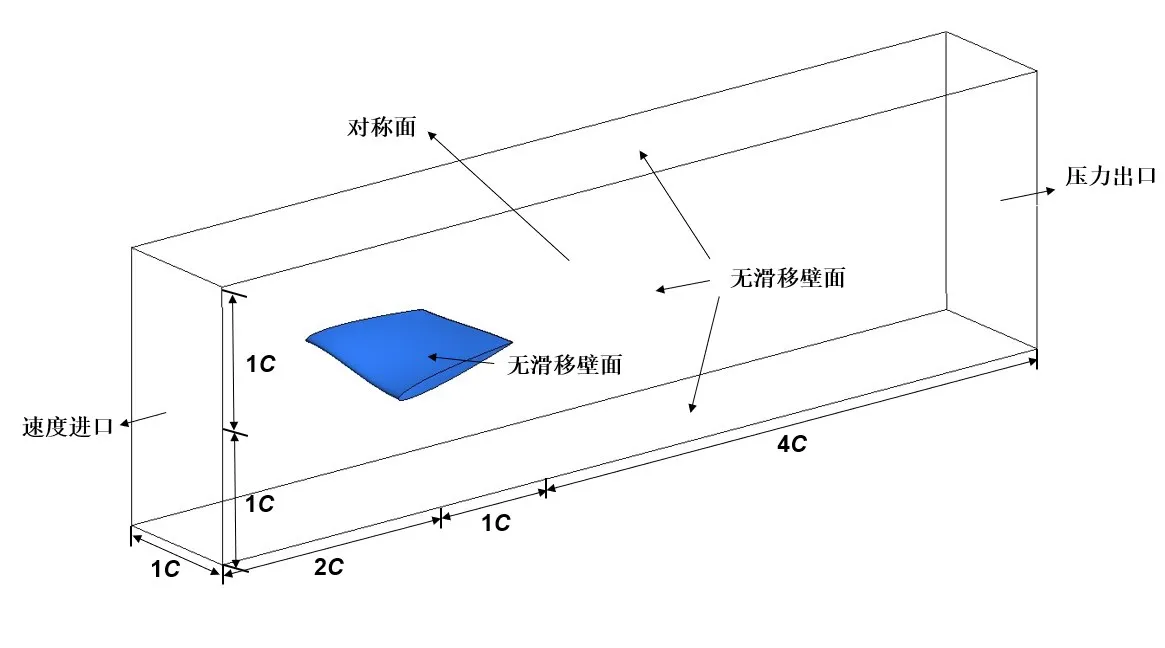
圖2 計算域及邊界條件Fig.2 Computational domain and boundary conditions

需要注意的是，為了節省計算資源，本文在數值模擬中僅對該水翼的一半進行了模擬計算，中間切面選取對稱面邊界條件，其余壁面均選取無滑移壁面條件。

圖3 給出了計算域內的網格劃分情況。為保證網格質量，全域均采用結構化網格。為精細地捕捉水翼吸力面的空泡結構演變特性，在水翼吸力面附近進行網格細化，在水翼壁面附近添加邊界層，使得壁面函數y+在1 左右。為兼顧計算效率與計算精度，參考Long 等[30]的工作，本文的總網格數取1100萬，非定常計算時間步長選取為Δt=1×10-5s。

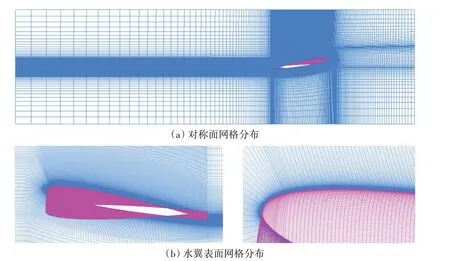
圖3 網格劃分情況Fig.3 Mesh generation

1.4 計算結果與對比分析

以數值模擬手段對空蝕風險預報的前提是該模擬獲得的空化流場形態應當與實際一致。為了驗證空蝕風險預報結果的準確性，本文在涂層試驗過程中使用高速攝影拍攝水翼吸力面的空化形態。試驗工況與數值模擬一致。

圖4 為一個脫落周期（T0）內水翼吸力面試驗空化形態與數值模擬蒸汽體積分數αv=0.1 的等值面圖像的對比。結果顯示，試驗和數值結果較一致地展現了片空化的產生、發展、脫落及潰滅的準周期過程。該工況下空化形態主要特點為：水翼兩側流動狀態相對穩定，片空化的脫落、再生過程集中在水翼中央；片空化充分發展時被向上游發展的回射流從導邊處切斷形成脫落云，見圖4（a）～（b）；隨后脫落云中間部分向上卷起，兩端附著在水翼表面，逐漸形成U型渦，見圖4（c）～（d）；脫落云與U 型渦隨主流向下游運動過程中，伴隨著大量空泡潰滅，直到U 型渦離開隨邊時，空泡幾乎全部潰滅，見圖4（e）～（f）。

圖4 水翼吸力面試驗中的空化形態與數值模擬αv=0.1 空化形態Fig.4 Cavitation morphology captured by test and iso-surface of αv=0.1 captured by numerical simulation on hydrofoil suction surface

2 空蝕風險涂層試驗

2.1 試驗設備及試驗方法

本次試驗主要設備包括循環式高速空泡水筒、高速攝影相機等。圖5為高速空泡水筒的示意圖。高速空泡水筒試驗段的長度為1600 mm，寬和高均為225 mm，最高水速為25 m/s，試驗段壓力可調整為5 kPa至500 kPa，邊壁為透明有機玻璃，以便高速攝影拍攝試驗情況。高速攝影采用3200 fps的拍攝頻率，對水翼的吸力面進行拍攝。

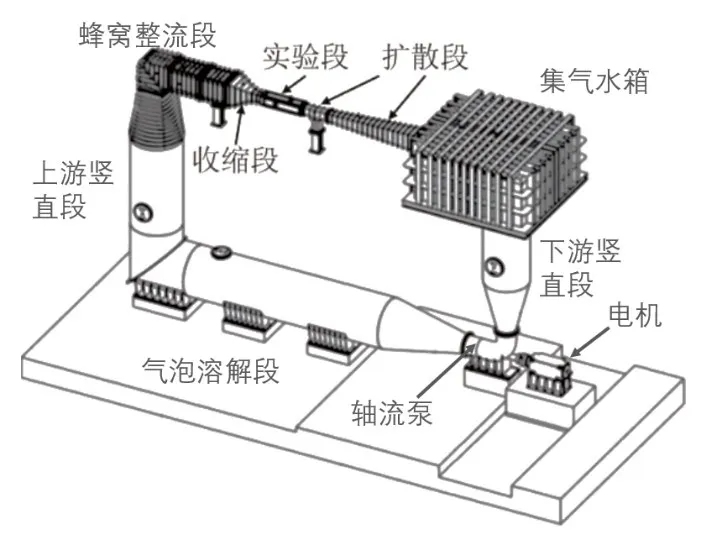
圖5 高速空泡水筒示意圖Fig.5 Schematic diagram of high speed cavitation tank

水翼模型參數與數值模擬模型完全相同，鋁合金材質，在水翼表面噴涂軟面材料，便于更快地觀測空蝕風險情況，試驗前水翼吸力面如圖6所示。本次水翼安裝采用0°攻角，吸力面朝下，在試驗段的安裝位置如圖7所示。

圖6 試驗前水翼吸力面Fig.6 Hydrofoil suction surface before test

圖7 水翼安裝位置Fig.7 Installation position of hydrofoil

試驗水速為14 m/s，試驗段空化數為1.2。涂層試驗始終在該工況下進行，試驗開始后，空化形態很快趨于穩定。試驗過程中，通過高速攝影判斷水翼空蝕風險的大致情況，當發現高速攝影中出現明顯的空蝕風險區域時，停止運行空泡水筒，再在無空化情況下確認空蝕風險區域是否形成。本次試驗進行1 h后，發現水翼吸力面出現了大量的空蝕風險區域，隨即停止試驗，將水翼從高速水洞中取出，觀察并記錄水翼表面空蝕風險情況。

2.2 涂層試驗空蝕風險結果及分析

空蝕風險試驗結果如圖8 所示。其中，黑色區域為涂層材料受到剝蝕的區域。圖8（a）中標出了空蝕風險區域，圖9則給出了相應區域的高速攝影典型空化形態。

圖8 涂層試驗空蝕風險結果Fig.8 Results of cavitation erosion risk

圖9 試驗空蝕風險結果與空化形態的對應Fig.9 Correspondence between cavitation erosion risk results and cavitation morphology

涂層試驗結果顯示，空蝕風險區域主要分為兩部分：主空蝕風險區域及條帶狀空蝕風險區域。其中主空蝕風險區域大約處于水翼弦向2/11弦長到8/11弦長之間，其空蝕風險最為嚴重，對應于片空化脫落區域。與主空蝕風險區域相連接的兩個條帶狀的空蝕風險區域一直延伸到隨邊，存在明顯的點狀空蝕風險區域，對應于U 型渦兩腿經過的區域。此外，U 型渦脫離開隨邊的位置處，空蝕風險明顯加重，對應于條帶狀空蝕風險區域與隨邊相連的位置，如圖9（b）中紅色箭頭指向的位置。

3 空蝕風險預報方法

3.1 空蝕機理回顧

空泡向水翼下游移動進入壓力恢復區域時，由于泡外壓力不斷增大，空泡開始潰滅。人們普遍認為，空蝕是蒸汽空泡潰滅引起的。對于初始半徑為a、初始泡壁速度為u0=0 的蒸汽空泡，不考慮表面張力、粘性、不可凝氣體在內的潰滅動力學方程，即R-P方程為

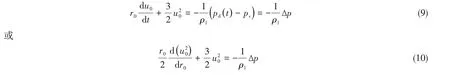
式中，r0為汽泡半徑，pd(t)為泡外壓強，pv為飽和蒸汽壓，ρl為液體密度。式（10）的解，即潰滅過程泡壁速度為

空泡收縮至潰滅的時間為

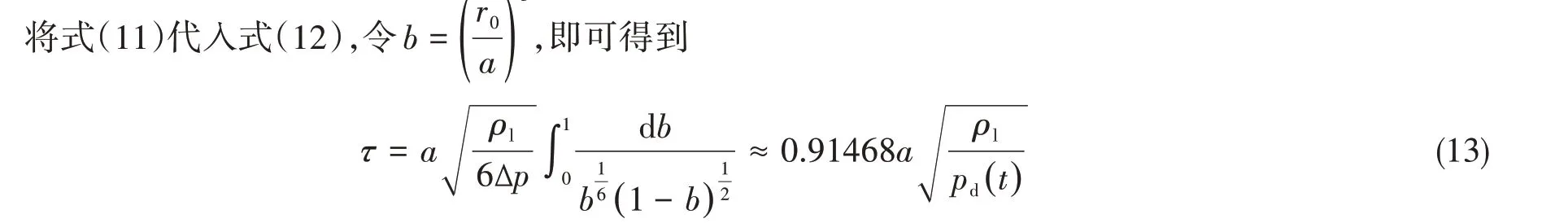
顯然，當空泡半徑r0→0，泡壁面流體沿徑向速度u0→∞。實際流動中，由于粘性泡內存在不可凝結氣體，使得空泡不能潰滅至半徑為0，泡壁面速度也不能達到無窮大。盡管如此，空泡潰滅至最小半徑時，其泡壁速度也將是很大的數值，這實際上就是造成空蝕的微沖擊波及微射流的來源。

當然，只有非常靠近壁面的空泡潰滅才對空蝕有貢獻，否則微沖擊波與微射流在尚未到達壁面時將衰減耗盡。此外，無論是球形繞流體近壁面的順流而下，還是球形泡的收縮都會產生趨壁效應[31]。定性而言，趨壁效應使得近壁面側壓力進一步降低，原本中心對稱的沖擊波在靠近壁面方向的強度會大于其他方向，而微射流的方向也會指向壁面，使得向壁面方向傳遞的能量更加集中。

所以，決定空蝕風險的主要是近壁面的流場，本文提出的空蝕風險參數，只需在貼壁流場中去判別與尋找。Phillip 和Lauterborn[32]也通過試驗證明了最大的沖擊載荷是由與壁面直接接觸的空泡潰滅造成的。

3.2 蒸汽泡潰滅的能量轉化過程

根據前述，本文兩相流的數值模擬方法與三維扭曲水翼空化流試驗結果吻合較好。但該兩相流數值模擬無法直接顯示蒸汽泡潰滅引起的徑向流場速度u0的時空分布，更無法表征微沖擊波與微射流。為此需要尋找其它表征潰滅的物理參數。

3.2.1 蒸汽泡勢能

將半徑為r0的單個蒸汽球泡與周圍半徑為R（R→∞）的球狀液體空間組成一個系統，如圖10所示。由于系統蒸汽泡內部氣壓為飽和蒸汽壓Pv，而系統外則為大于飽和蒸汽壓的當地壓力Pd(t)，因此，在t時刻系統內外存在壓差Pd(t)-Pv。

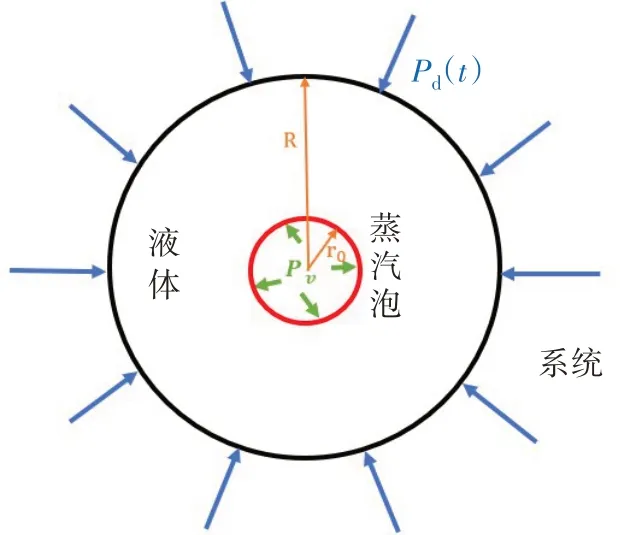
圖10 單空泡潰滅模型Fig.10 Single bubble collapse model

收縮過程中，蒸汽球泡泡徑為r0時，若泡徑變化dr0，pv對液體作負功為

泡外充滿水的充分大半徑為R的同心球體因連續性方程同時需縮小dR，有

pd(t)對液體作正功為

故泡收縮時，外力對液體實際作功為

式中，Vv為蒸汽泡的體積。

因此，當蒸汽泡收縮dVv時，外力對泡外液體作功dW；而蒸汽泡損失的勢能為

蒸汽泡潰滅釋放出全部勢能

3.2.2 潰滅過程中蒸汽泡的勢能轉化為流場的動能

初始泡壁速度為0的空泡，當半徑由a縮減至任意值r*≤a時，空泡的勢能減小為

式中，u*為泡壁r*處的速度。

當空泡半徑由a縮減至r*時，流場動能增加為

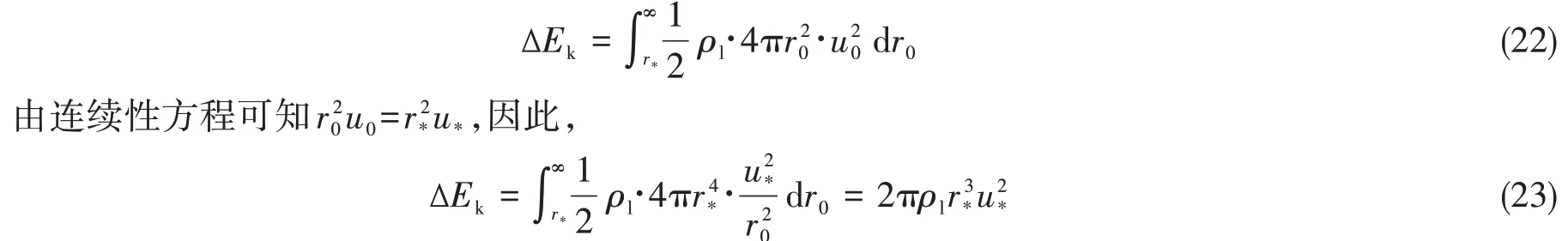
則ΔEp=-ΔEk。可知蒸汽泡減小的勢能全部轉化為周圍流場的動能。所以，尋求蒸汽泡潰滅所引起的流場動能的時空分布，可以等價轉換為尋求流場蒸汽泡勢能減少的時空分布。

3.3 空蝕風險表征

本文采用的S-S 空化模型中選用單位體積液體氣泡數密度為n=1×1013，空蝕風險是群泡的物理行為，就是對單位體積中存在的1×1013個蒸汽泡的時空特性的描述。

3.3.1 空蝕風險表征參數的選取

（1）環境壓強

式（10）可改寫為

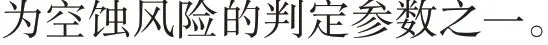
（2）環境壓強變化率

（3）壁面累積能量

由于目前數值模擬尚不能給出空泡群潰滅過程準確定量的描述，且空蝕風險預報無需定量確定壁面用于剝蝕能量的大小，只需要一個相對值。但有一點可以肯定的是，近壁面流場釋放的空泡潰滅的能量越大越多，壁面累積的用于空蝕的能量便越多，空蝕就越容易發生，空蝕程度就越嚴重。

式（18）給出了單泡潰滅時勢能釋放的表達式，則對于群泡，在單位體積中釋放的勢能變化率為

式中，αv為單位體積的蒸汽體積分數，ep為單位體積泡群釋放的勢能。

因為空蝕是微沖擊波與微射流長期作用在壁面上的結果，參數一、二的滿足可視為單次沖擊具備了引起空蝕風險的潛力，但需要多次類似的沖擊疊加才可能導致空蝕。考慮到空化流的非定常特性，故選取一充分長的時間T，將壁面累積的空泡潰滅過程中釋放的勢能值超過閾值C2作為參數三。

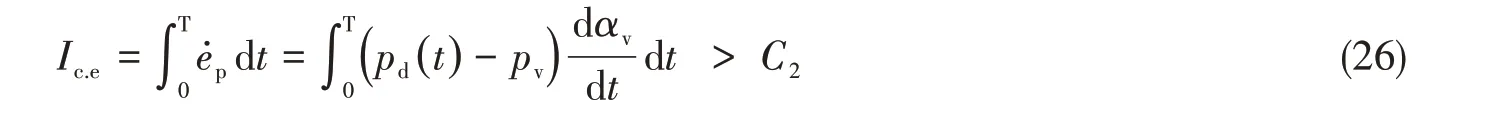
3.3.2 空蝕風險表征方法

（3）壁面空蝕風險表征參數三為Ic.e＞C2。

根據前人的研究，本文在計算壁面累積能量Ic.e時采用了時間平均壓力場pˉd(t)作為驅動空泡潰滅的環境壓力場[28]。

需要說明的是，式（26）中蒸汽體積分數變化率項若使用物質導數的展開式進行計算，其時間偏導數項及對流項均需采用差分格式，若無法保障數值計算結果的時間步長足夠小及網格分辨率足夠低，將會對計算精度產生較大影響。本文采用傳質源項對蒸汽體積分數變化率進行替代，式（6）將蒸汽體積變化與相變過程中的傳質源項聯系起來，傳質源項的表達式見式（7），可發現其全部變量數據取自當前時間步，且無需求解對流項，因此解決了差分格式帶來的誤差問題，相對而言，精度更高。根據式（6）～（7），潰滅過程中的蒸汽體積分數變化率可表示為

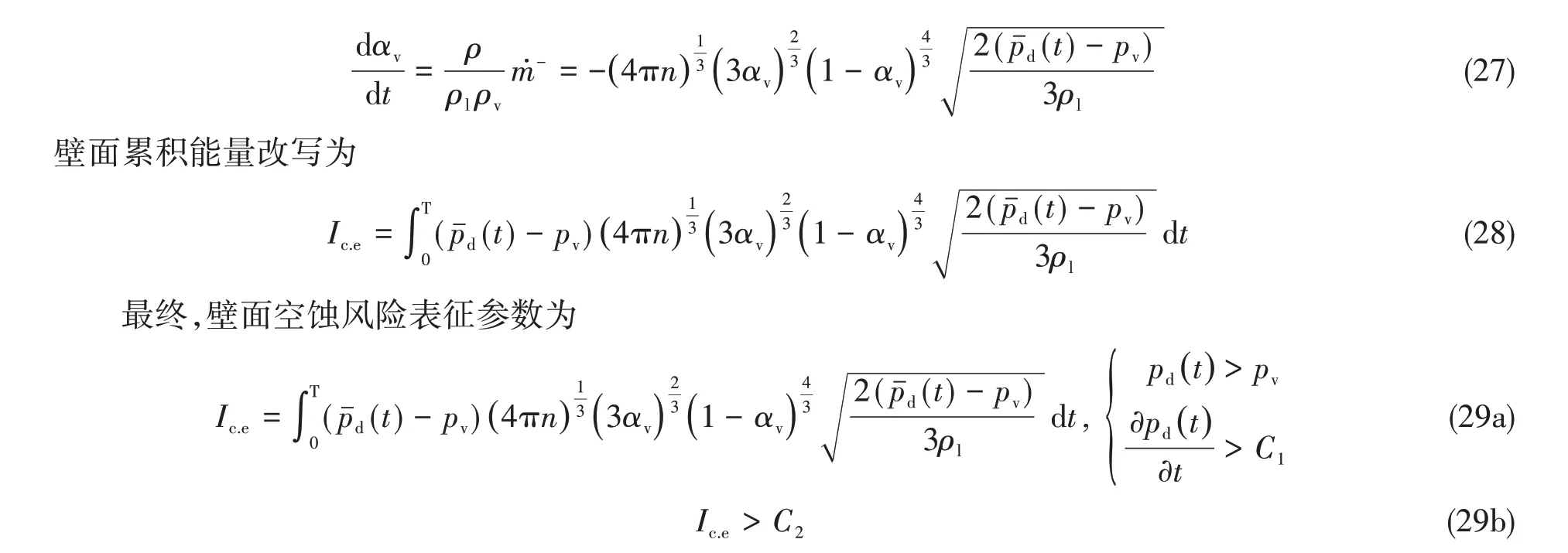
在滿足當地壓強大于飽和蒸汽壓，壓強隨時間變化率大于閾值C1的條件后，計算壁面累積能量Ic.e，壁面累積能量大于C2可視為該區域存在空蝕風險。

3.4 空蝕風險預報結果

3.4.1 閾值C1、C2的選定

閾值C1、C2作為壓強隨時間變化率及壁面累積能量的下限，共同決定了空蝕風險區域的范圍。在此基礎上，壁面累積能量Ic.e的相對大小則可表征空蝕風險的嚴重程度。

分別選取閾值C1=2×105、1×106、5×106及C2=1×1010、2×1010、3×1010，將閾值C1、C2兩兩配對計算水翼表面的空蝕風險。由此得到9個空蝕風險預報結果，并將其與試驗空蝕風險區域進行比較，如圖11所示。可以看出，隨著閾值C1的增加，水翼中前部的空蝕風險區域逐漸縮小，中后部空蝕風險越來越明顯；隨著閾值C2的增加，空蝕風險區域的外圍輪廓，尤其是水翼導邊附近區域隨之縮減。通過比較，與試驗結果吻合最好的為圖11（e）。因此選定閾值C1=1×106，C2=2×1010。

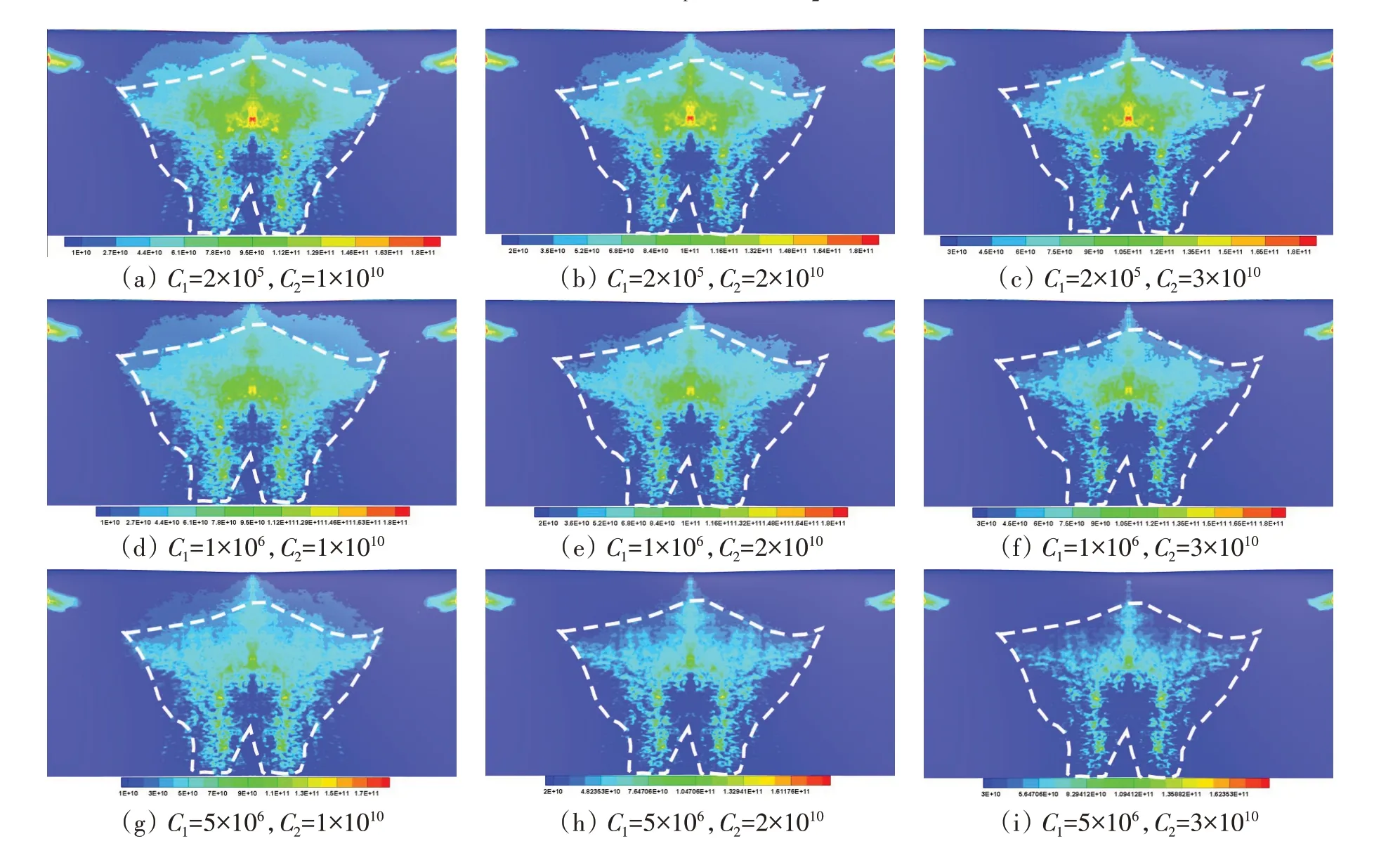
圖11 9組閾值計算的空蝕風險預報結果與試驗結果比較Fig.11 Prediction results of cavitation erosion risk calculated by 9 groups of threshold values compared with the experimental results

3.4.2 空蝕風險預報結果

圖12 為采用基于傳質源項的空蝕風險預報方法得到的空蝕風險預報結果與試驗結果的對比。可以看出，空蝕風險預報結果在片空化脫落的區域預報出了空蝕風險，同時在U型渦經過的位置也預報出了兩個條帶狀的空蝕風險區域，與試驗結果顯示的空蝕風險區域基本吻合。此外，預報結果顯示片空化脫落區域的空蝕風險程度更為嚴重，與試驗結果亦較為吻合。盡管預報結果與試驗結果在大部分區域吻合較好，但預報結果顯示在水翼兩端即紅框范圍內存在空蝕風險區域，與試驗結果不同。數值模擬和試驗顯示在水翼兩端的空化形態為片空化的周期性波動，與水翼中央出現的云空化不同，片空化周期性變化引起的空蝕風險預報方法需進一步研究。

圖12 空蝕風險預報結果與試驗結果的對比Fig.12 Comparison between cavitation erosion risk prediction results and painting test results

4 結 論

本文以NACA 0009 三維扭曲水翼為數值模擬及涂層試驗對象，將數值模擬空化形態與試驗高速攝影結果進行了對比。基于單個蒸汽球泡的潰滅模型，分析了潰滅過程中能量轉化過程及相質量的轉化過程，提出了空蝕風險的三個表征參數，并合理選定了表征參數的閾值。基于該方法，本文對繞NACA 0009 三維扭曲水翼表面的空蝕風險進行了預報，并與涂層試驗結果進行了對比分析。主要結論如下：

（1）采用大渦模擬方法可較好地捕捉繞NACA 0009 三維扭曲水翼空化流動的初生、發展、脫落、潰滅等過程，與試驗結果吻合較好；

（2）提出空蝕風險預報的三個表征參數：當地壓強、當地壓強變化率及壁面累積能量Ic.e。在當地壓強大于飽和蒸汽壓及當地壓強變化率大于閾值C1的前提下，通過壁面累積能量Ic.e大于閾值C2可以劃定空蝕風險的區域，通過Ic.e的大小可以判定區域內空蝕風險的相對嚴重程度。其中，Ic.e的求解采用了基于傳質源項的表達，避免了數值誤差。

（3）通過與涂層試驗比較，本文建立的空蝕風險數值預報方法獲得的空蝕風險結果與試驗空蝕風險結果在大部分區域吻合良好。兩者顯示的空蝕風險區域主要分為兩部分，一是位于片空化脫落的區域，二是位于U型渦兩腿經過的區域，其中片空化脫落區域空蝕風險更為嚴重。

雖然本文空蝕風險預報僅對三維扭曲水翼進行了驗證，而且閾值C1、C2的確定帶有經驗性質，但因為三個空蝕風險參數均建立于空蝕機理之上，所以具有一定的普適性。下一步將研究如何將閾值C1、C2與影響空蝕的物理量聯系起來，從理論上確定閾值C1、C2。