改進A*算法的路徑規劃在列檢環境中的應用

郭大林，王淑營，曾文驅，楊 娟

(1.西南交通大學 唐山研究生院，河北 唐山 063000；2.西南交通大學 計算機與人工智能學院，四川 成都 611756；3.廣州地鐵設計研究院股份有限公司 自動化和通號所，廣東 廣州 510010)

0 引 言

隨著我國機器人智能化水平不斷提高，自動導引車(automated guided vehicle，AGV)的應用隨處可見。比如柔性制造系統(flexible manufacturing system，FMS)[1]、大型智能化碼頭[2]、智慧物流倉庫[3]以及智能地下停車場[4]等。AGV路徑規劃是AGV應用研究的重要基礎問題之一[5]，指的是在一個存在障礙物的環境中，AGV小車按照時間最短或路徑最短等性能指標從起點到終點找到一條安全無碰撞路徑[6]。目前主要的路徑規劃算法有迪杰斯特拉(Dijkstra)算法[7]、A*算法[8]，除此之外還有蟻群算法[9]、遺傳算法[10]等。A*算法是一種基于全局最優的啟發式搜索算法，能夠快速尋找最優解的同時，避免陷入局部最優問題。但是A*算法在實際應用中存在搜索的轉彎次數頻繁導致路徑呈階梯狀，搜索節點數量大導致效率低下等問題，對此，國內外學者進行了大量改進研究。呂云峰[11]提出一種變步長優化傳統A*算法，該算法在傳統A*算法規劃出路徑結果之后，重新剔除路徑上的冗余節點，從而減少轉彎次數；李紅[12]提出一種轉彎因子在A*算法尋路過程中減少大量的轉彎來平滑路徑。但這兩種算法均未提升搜索效率。吳鵬等[13]提出一種簡單的雙向搜索A*算法，從正向和反向兩個方向交替搜索來提高尋路效率，但該算法犧牲了最優路徑。孔繼利等[14]在雙向搜索算法的基礎上對啟發式函數重新加權，減少了搜索的節點量。而Lin等[15]利用當前搜索節點的父節點對啟發式函數的影響來優化路徑，從而縮短搜索時間，但是該算法同樣以犧牲最優路徑為代價。趙曉等[16]提出一種結合跳點搜索的改進A*算法，通過跳躍搜索標志性節點來減少搜索的節點數，但是環境中障礙物較多時，反而降低了算法的求解速度。

本文在不犧牲最短路徑的情況下，為避免AGV頻繁轉向，并進一步提高路徑尋優的效率，設計在傳統A*算法的啟發函數中引入轉彎懲罰機制用以平滑路徑，同時增加“選擇因子”,用以控制相同代價節點的選擇，來對傳統A*算法進行優化。并通過實驗結果驗證改進算法的可行性。

1 環境建模

目前，AGV常常使用柵格法[17]、拓撲地圖法[18]等地圖進行路徑規劃研究，由于使用柵格法建立的環境地圖能夠更加直觀表示地圖信息，同時也利于算法程序的編寫，所以本文將采用柵格法進行建模。常用的柵格地圖如圖1所示，柵格分為兩種：

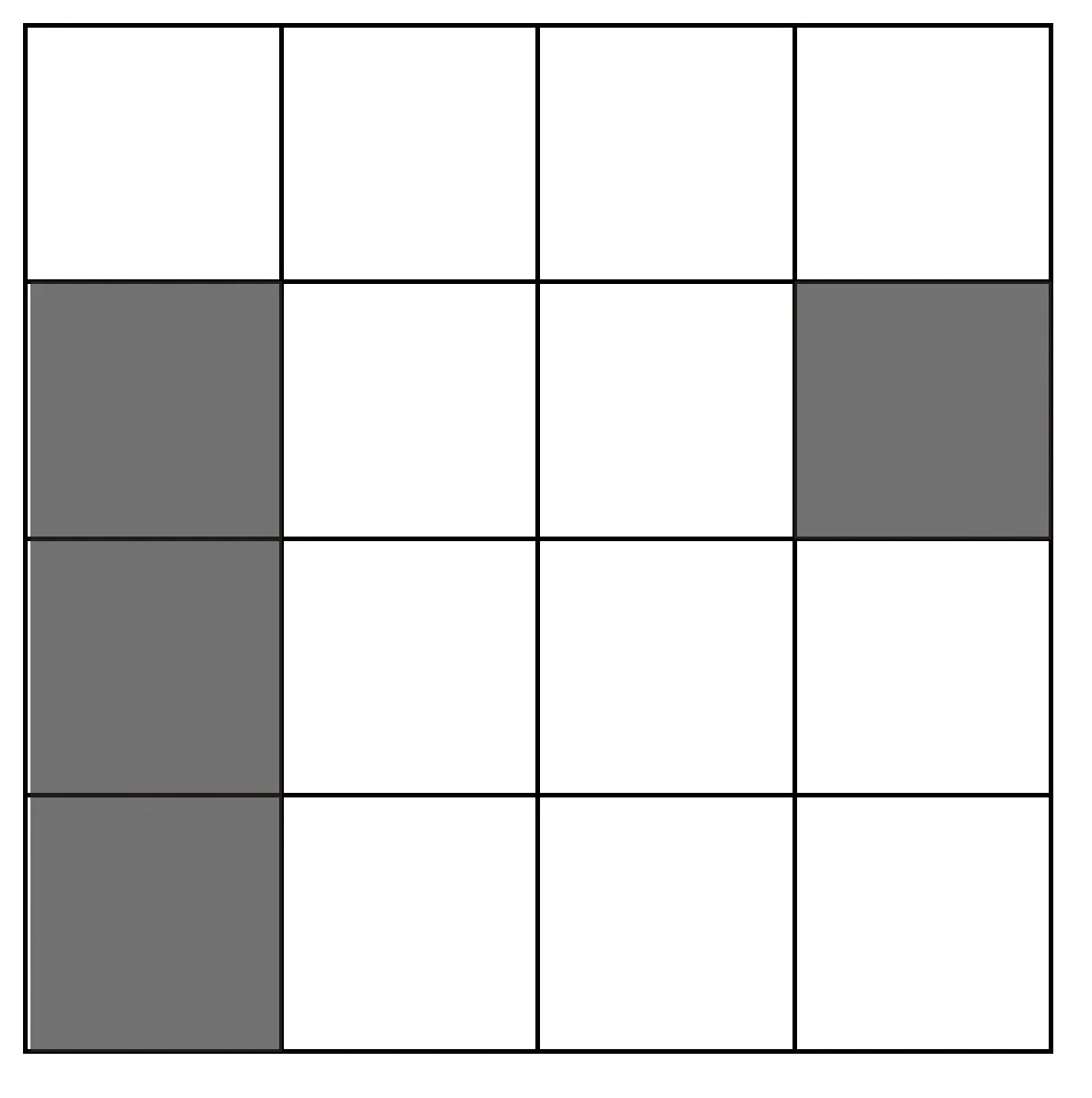
圖1 普通柵格地圖

黑色節點：障礙物。

白色節點：可通行節點。

在實際的列檢環境中，節點類型比較復雜，如圖2所示，主要分為4種：

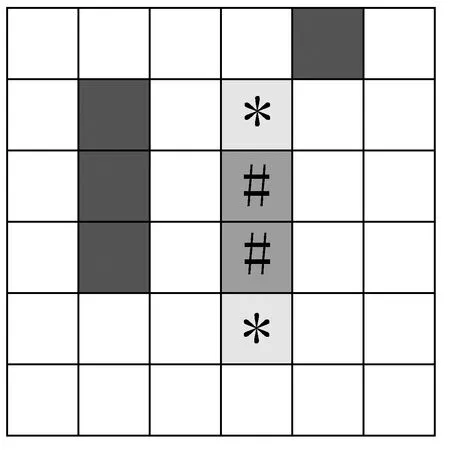
圖2 列檢環境柵格地圖

黑色節點：障礙物。

白色節點：可通行普通節點。

*節點：可通行升降平臺節點。

#節點：可通行檢測軌道節點。

其中升降平臺節點成對出現，位于檢修軌道節點的首尾處。根據列檢環境的實際需求，AGV運行規則做出如下假設：

(1)AGV在某些方向(45°方向)行走中可能會與障礙物角發生碰撞，造成損失。故如圖3中箭頭方向所示，本文AGV行走只考慮上下左右4個方向；

(2)在柵格地圖中，障礙物節點無法通行，普通節點與升降平臺節點AGV可以4個方向通行，檢測軌道節點左右通行會碰撞墻壁，故只能上下通行；

(3)在柵格地圖中，AGV通行規則如圖3所示。

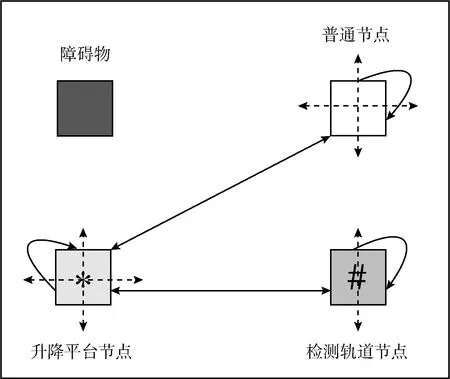
圖3 節點通行方向與規則

障礙物節點：AGV無法通行。

普通節點：AGV可以直接到達普通節點、升降平臺節點，無法直接到達檢修軌道節點。

升降平臺節點：AGV可以直接到達普通節點、升降平臺節點、檢修軌道節點。

檢測軌道節點：AGV只能到達升降平臺節點和其它同一檢修軌道節點。

(4)AGV勻速運行，不考慮起始點出發時加速和到達目的地減速的過程。

2 傳統A*算法

A*算法是一種全局最優的啟發式搜索算法，它是通過估價函數來確定搜索前進的方向，從而不斷向目標節點不斷靠近，避免在搜索過程中的盲目性。其表達式如式(1)所示

f(n)=g(n)+h(n)

(1)

式中：n為當前被搜索節點，f(n)為從起點通過n節點再到目標節點m的估計代價，它由g(n)和h(n)兩部分組成。其中g(n)表示起點到當前節點n的實際所花費的代價，如果路徑搜索中函數g(n)的值一直取0，則估價函數所表示的算法退化為廣度優先搜索(BFS)算法，h(n)表示當前節點n到目標節點m的估計最短距離，h(n)常常選用歐式距離、曼哈頓距離或切比雪夫距離計算，其對應表達式分別如式(2)～式(4)所示

(2)

h(n)=|xn-xm|+|yn-ym|

(3)

h(n)=max(|xn-xm|,|yn-ym|)

(4)

如果路徑搜索中函數h(n)的值一直取0，則估價函數所表示的算法退化為Dijkstra算法。要保證算法找到的解是最優解，則需要保證函數h(n)的值始終小于等于實際節點n到終點m的距離。

傳統A*算法主要核心即是維護open列表和close列表，其主要處理流程如下：

(1)初始化open列表和close列表，并把起點加入open列表中。

(2)重復如下步驟：

1)遍歷open列表，查找f(n)值最小的節點，把它移到close列表中，并把它作為當前要處理的節點，記為節點n。

2)遍歷節點n的上下左右相鄰節點，忽略不可達節點和已在close列表的節點。如果這些可達節點不在open列表中，則添加到open列表，并把節點n設為該節點的父節點，再計算它的g(n)值和f(n)值。如果該節點已經在open列表中，則比較當前路線的g(n)值和原線路g(n)值，如果當前線路更好，即當前路線的g(n)值更小，則更新該節點在open列表中的g(n)值和f(n)值信息，并把節點n設為該節點的父節點。

(3)終止條件：

1)open列表為空，說明此次尋路搜索失敗，無法規劃出一條到終點的路徑，此時輸出提示信息。

2)open列表中加入了終點，說明此時路徑已經找到，輸入路徑信息。

傳統A*算法的處理流程如圖4所示。

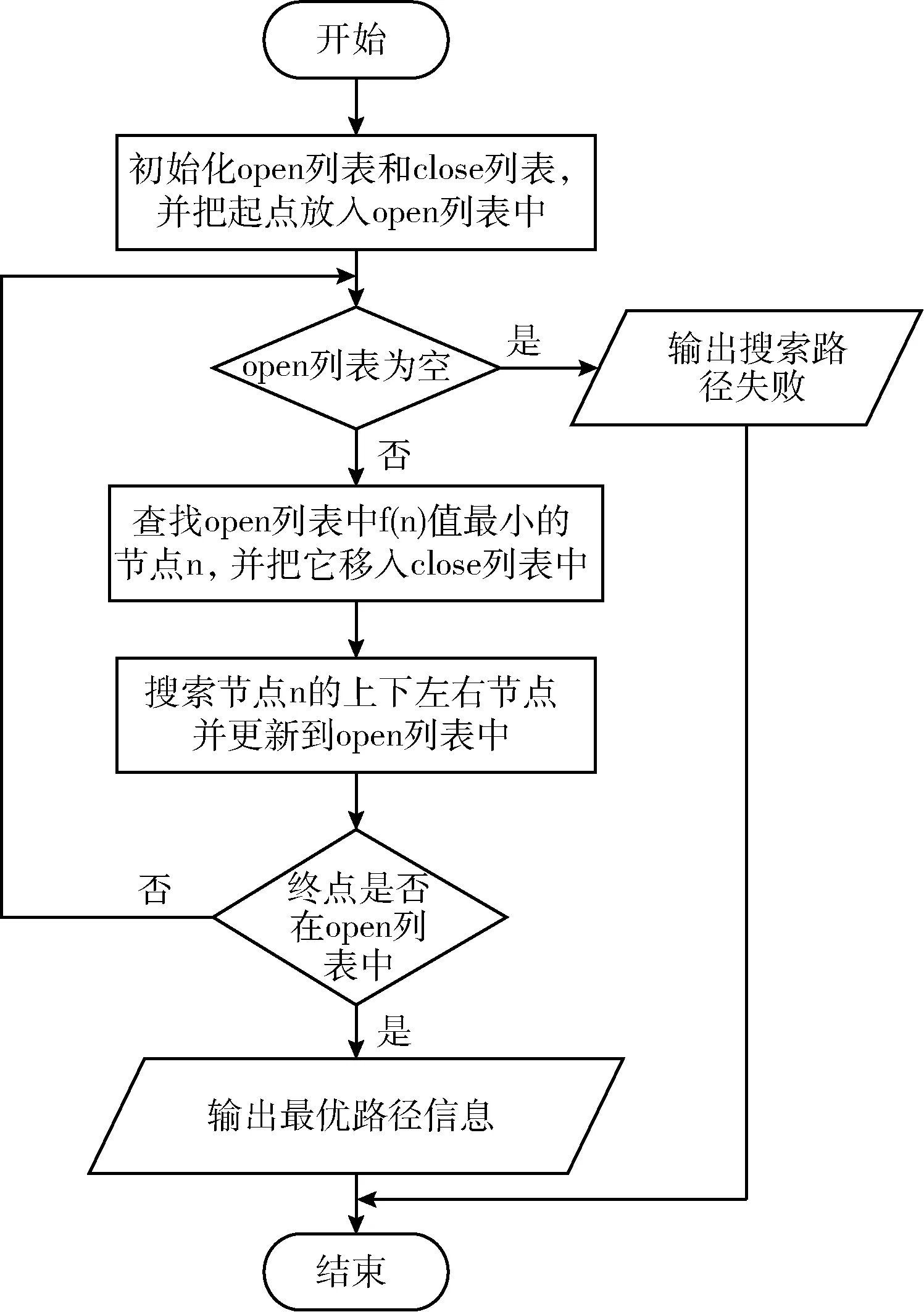
圖4 傳統A*算法處理流程

3 改進A*算法設計

3.1 傳統A*算法的不足與改進

在采用傳統A*算法的AGV系統中，當某些節點的代價f(n)相同的時候，選擇不同的節點進行遍歷，最終總的搜索節點數不同，極端情況下它們可能都會被搜索一遍，盡管有時候我們只需要搜索其中的一條便能到達最終節點，本文使用曼哈頓距離度量兩點間的預估代價，如圖5地圖所示，start節點表示起點。end節點表示終點。黑色節點表示障礙物。此時地圖中存在A，B兩個代價f(n)相同的節點。

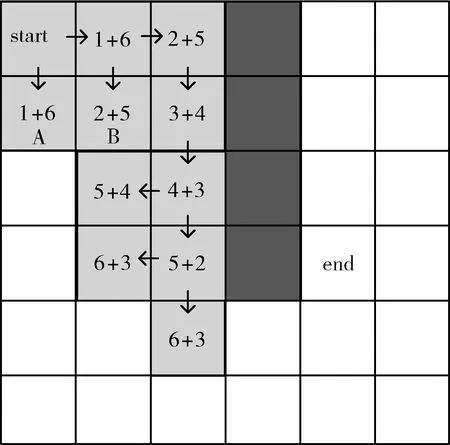
圖5 相同代價節點

如圖6斜杠節點所示，當選擇A節點作為當前處理節點，最終遍歷節點總數為23個。

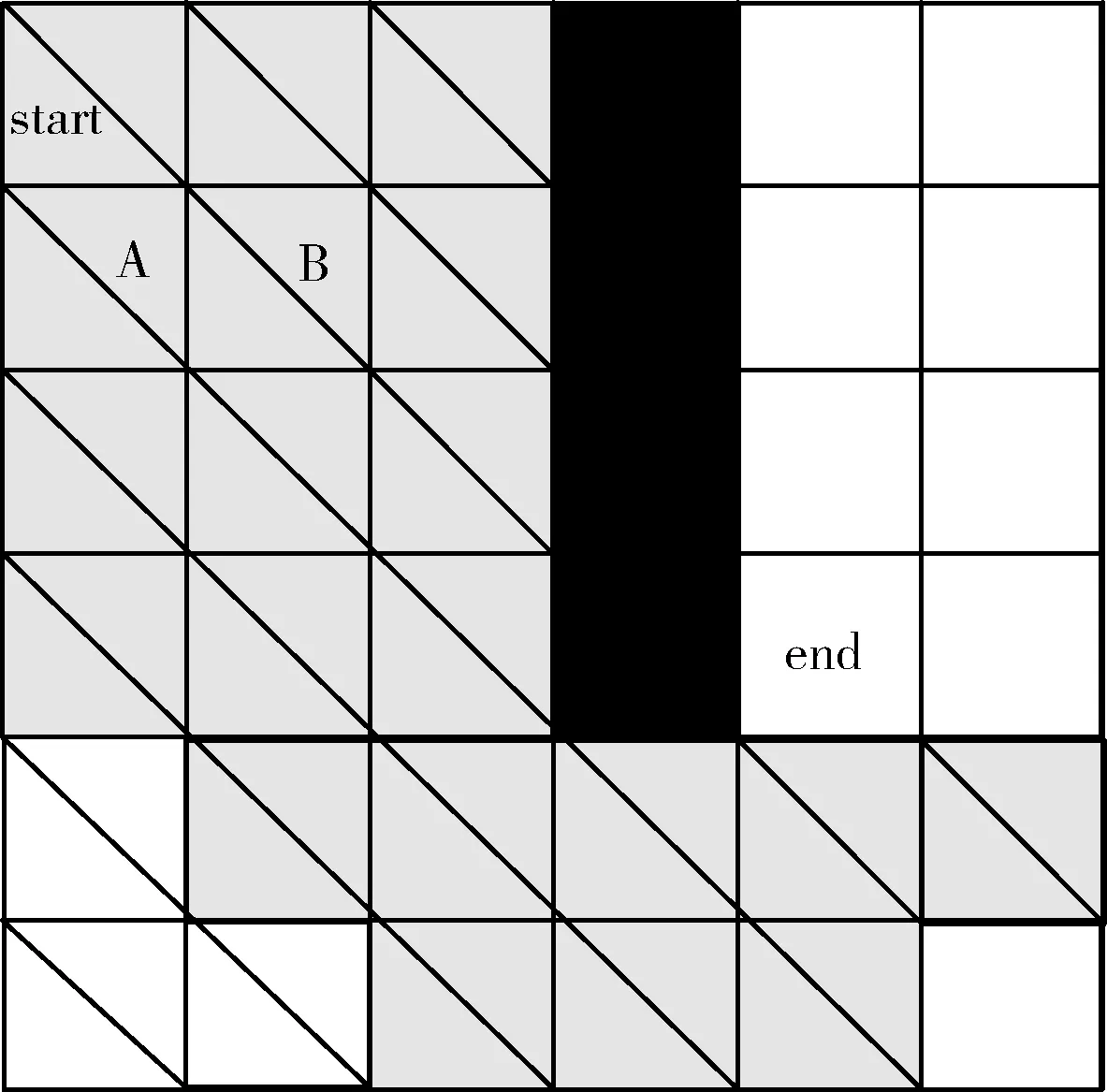
圖6 分別采用A和B節點的遍歷節點數

如圖6灰色節點所示，當選擇B節點作為當前處理節點，最終遍歷節點數20個。

因此，相同f(n)代價節點的選擇導致額外遍歷節點，使計算量增加也是傳統A*算法性能較低的一個原因。為了解決這個問題，本文在啟發式函數中增加一個“選擇因子”β，使其作用于h(n)函數上，從而讓傳統A*算法中那些具有相同的f(n)代價節點體現出區別。因為A*算法會根據f(n)值對節點排序，尋找最小代價節點時，讓f(n)值不同意味著只有一個唯一的最小f(n)值的節點被選取。同時，“選擇因子”β產生的附加值添加到h(n)函數上能夠使得A*算法搜索過程中傾向于向目標結點擴展，減少A*算法遍歷的節點總數。當然，“選擇因子”β產生的附加值不宜過大，否則會導致h(n)值偏大，A*算法退化為BFS算法。具體設計如下

f(n)=g(n)+h′(n)

(5)

h′(n)=(1+β)*h(n)

(6)

如式(5)、式(6)所示，修改傳統估價函數h(n)的計算方式，增加“選擇因子”β，從而使open列表中的節點具有唯一的f(n)值，減少A*算法遍歷的節點數。如圖7所示，當增加的“選擇因子”β根據h(n)函數為每個節點產生額外附加值時，由于B節點的h(n)函數值小于A節點，產生的附加值k2小于k1，從而B節點的f(n)值小于A節點。因此A*算法將選擇遍歷節點數小的B節點作為當前處理節點。

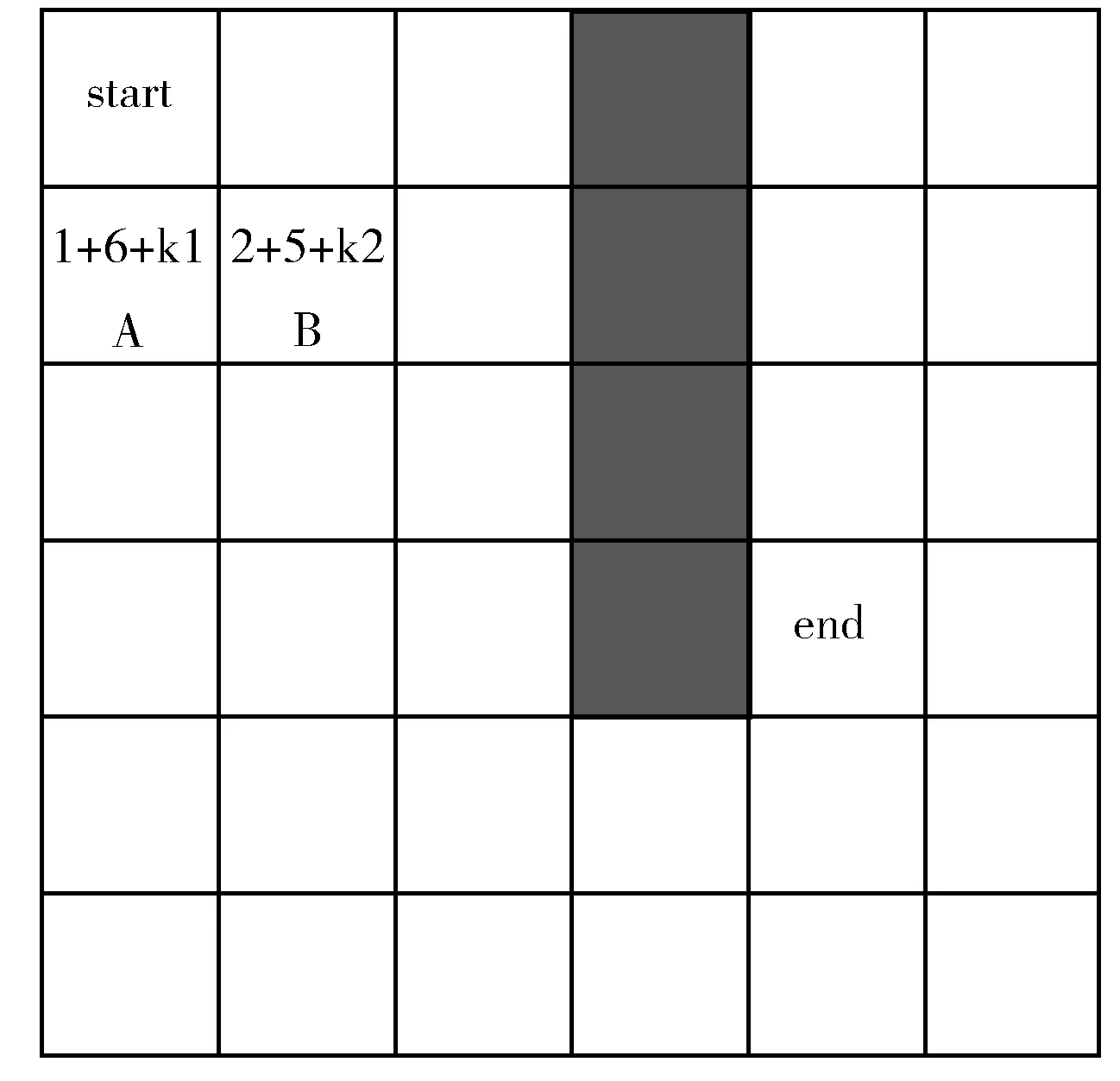
圖7 帶“選擇因子”的相同代價節點

另一方面，在傳統A*算法在路徑規劃時，代價函數只考慮起始節點到當前節點的實際路徑和當前節點到目標節點的估計路徑。這種簡單的啟發式函數帶來的后果是導致AGV路徑規劃中路徑不平滑，呈階梯形，特別是在開始階段和結束階段比較明顯。頻繁的改變AGV移動方向勢必會對AGV造成更多能耗，同時轉向也會導致AGV減速，行駛效率大大降低。因此本文針對此問題引入轉彎懲罰機制，對于那些需要轉彎的節點增加相應的懲罰代價。具體設計如下

f(n)=g(n)+h(n)+αT

(7)

如式(7)所示，在傳統估價函數f(n)中加入額外懲罰代價αT用于懲罰轉彎節點，其中α取值范圍為(0,1)，T為轉向次數。因此本文最終使用的啟發式函數如式(8)所示

f(n)=αT+g(n)+(1+β)*h(n)

(8)

3.2 改進A*算法的參數確定

在啟發式函數的參數α、β確定過程中，本文選擇50*50的普通柵格地圖進行測試。每組參數測試5組用例，每組測試用例使用相同的起點和終點，記錄不同參數下路徑規劃遍歷的節點數、轉彎次數和路徑長度。首先確定參數α，通過實驗發現：α的取值不影響搜索路徑長度，無論α為何值，搜索路徑長度均不變。如圖8所示，不同測試用例的轉彎次數在α≠0時，都能明顯減少AGV轉彎次數(由于圖8中轉彎次數最終收斂為2次或3次，所以導致線段重疊只能看到兩條線段)。

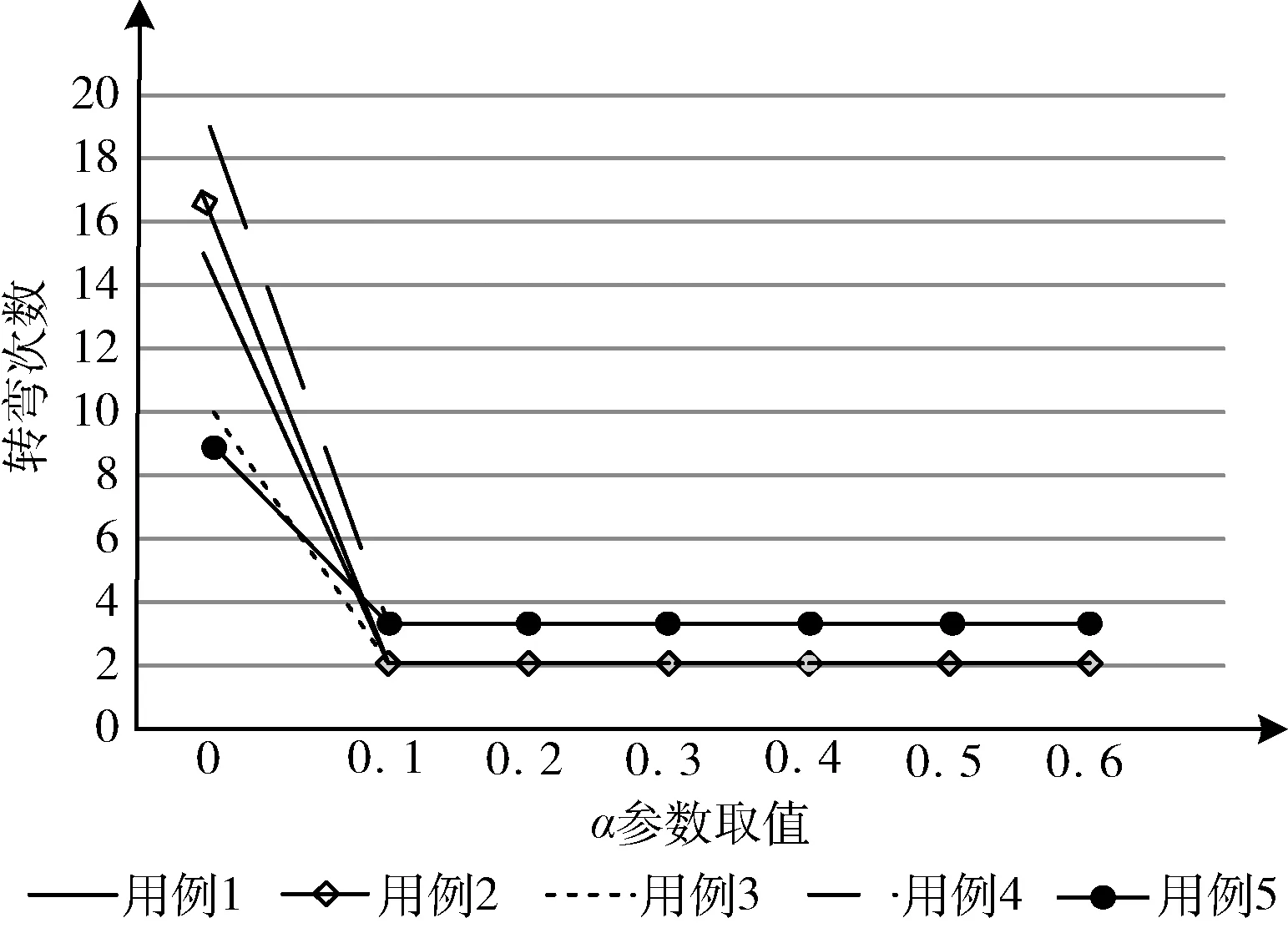
圖8 不同α取值轉彎次數

每組測試用例在α取不同值時遍歷的節點數如圖9所示，由圖可知，當α=0.3時，都能保證遍歷節點數最少。

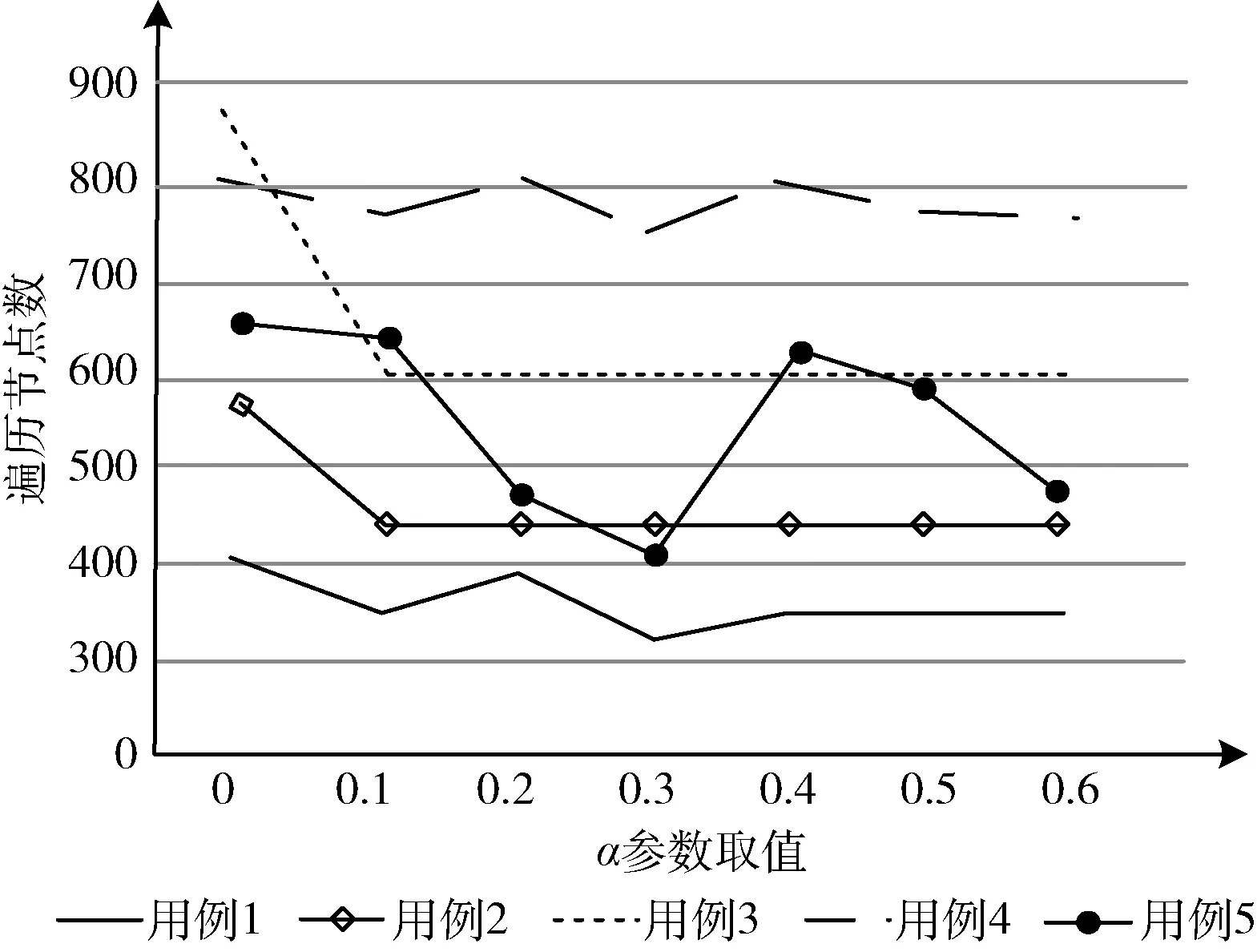
圖9 不同α取值遍歷節點數

確定參數β同樣選擇50*50的普通柵格地圖、測試5組用例，記錄不同參數下路徑規劃遍歷的節點數和路徑長度。通過實驗發現，如圖10所示，β的取值不影響搜索路徑長度，無論β為何值，均能夠獲取到最短路徑長度。如圖11所示，β=0時，遍歷節點數較多，β≠0時能夠明顯減少額外節點的遍歷，大大減少路徑搜索中節點遍歷總數。

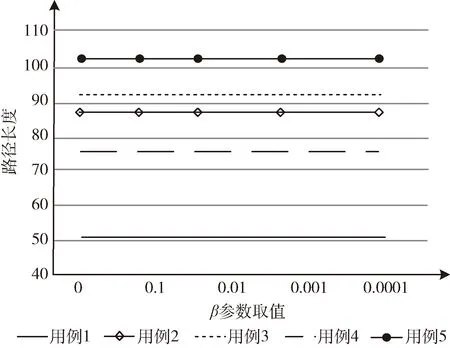
圖10 不同β取值最優路徑長度

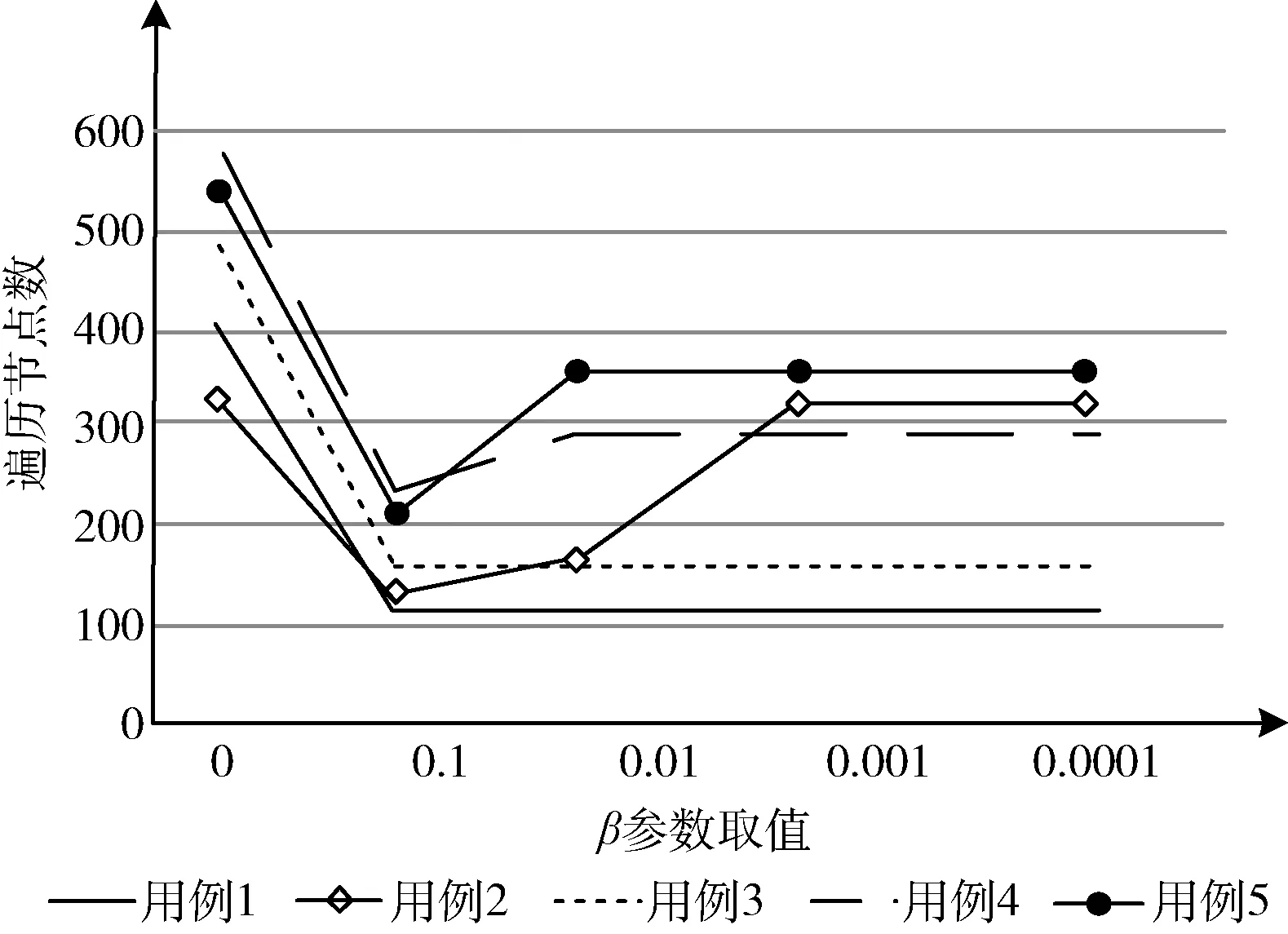
圖11 不同β取值遍歷節點數

當β=0.001之后遍歷節點數能夠收斂于同一數值。而在β=0.1時，能夠保證遍歷的節點總數最少。

綜上實驗結果，本文最終確定參數α取值為0.3，參數β取值為0.1。啟發式函數如式(9)所示

f(n)=0.3T+g(n)+(1+0.1)*h(n)

(9)

4 實驗設計與分析

4.1 仿真實驗分析

本文選擇50×50尺寸的普通柵格地圖進行實驗。與傳統A*算法、文獻[12]提出的改進A*轉向算法進行比較。來驗證本文提出的改進A*算法路徑尋優的性能。

在地圖中：

白色節點：可通行節點。

黑色節點：障礙物節點。

灰色節點：尋找最優路徑遍歷過的節點。

最終路徑規劃結果如圖12所示。

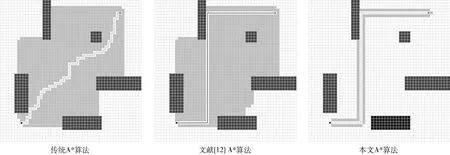
圖12 50×50柵格地圖不同A*算法結果對比

不同算法在50×50普通柵格地圖中的對比見表1。

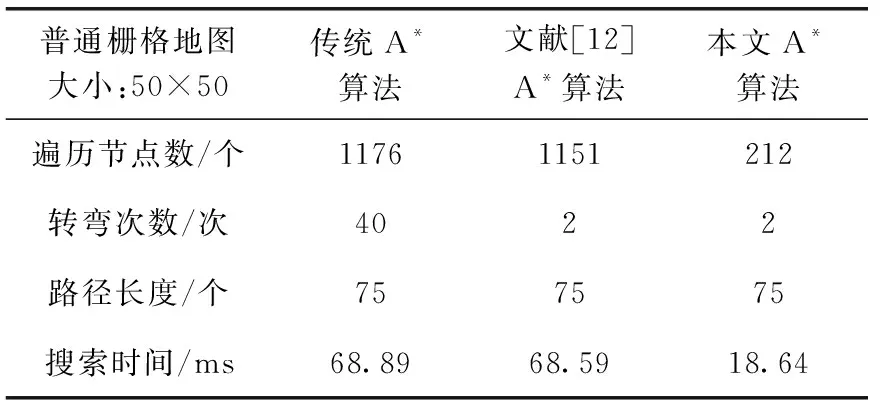
表1 不同算法在50×50地圖中的對比

由上述實驗結果可知，3種算法都能保證尋找最短路徑，但是傳統A*算法遍歷節點量大，轉彎次數較多。文獻[12]提出的算法雖然夠減少轉彎次數，遍歷節點數并沒有提高，使得整體搜索效率并沒有多大的提升，與傳統A*算法時間花費相當。本文提出的A*算法能夠明顯減少轉彎次數，并且大大減少節點的遍歷數，搜索時間明顯較小，搜索效率較高。

為了驗證本文算法在不同尺寸的地圖中的性能，分別在尺寸為25×25地圖、50×50地圖、75×75地圖、100×100地圖中分別進行實驗。和Dijkstra算法、蟻群算法、傳統A*算法、文獻[12]的A*算法進行對比驗證。實驗結果見表2～表5。

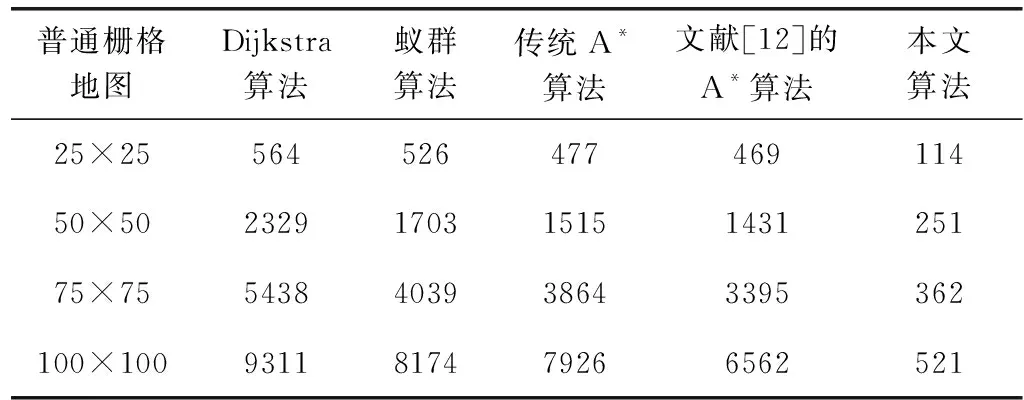
表2 不同算法遍歷節點對比/個

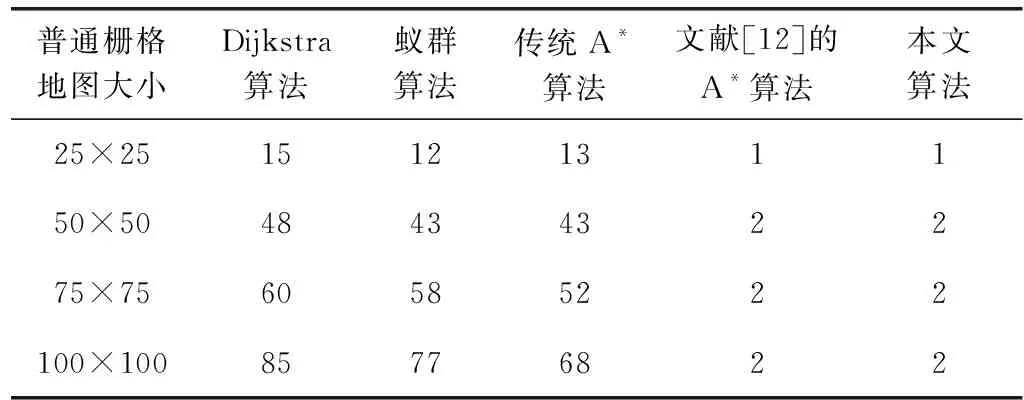
表3 不同算法轉彎次數對比/次

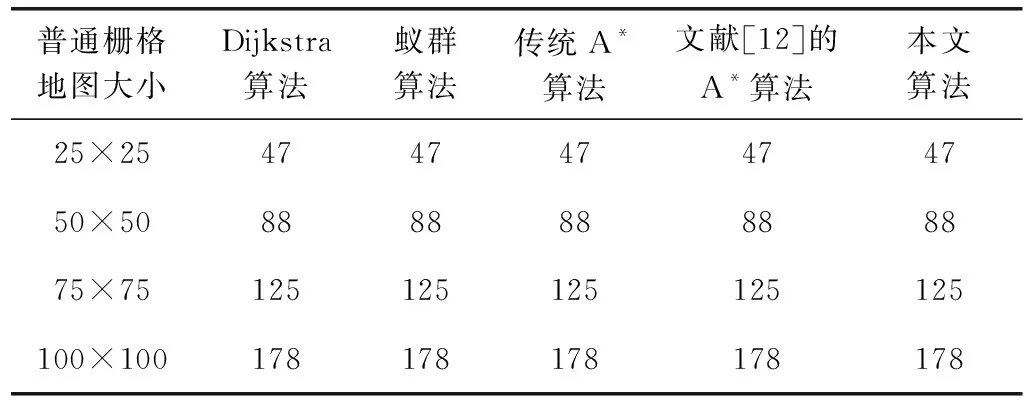
表4 不同算法路徑長度對比/個

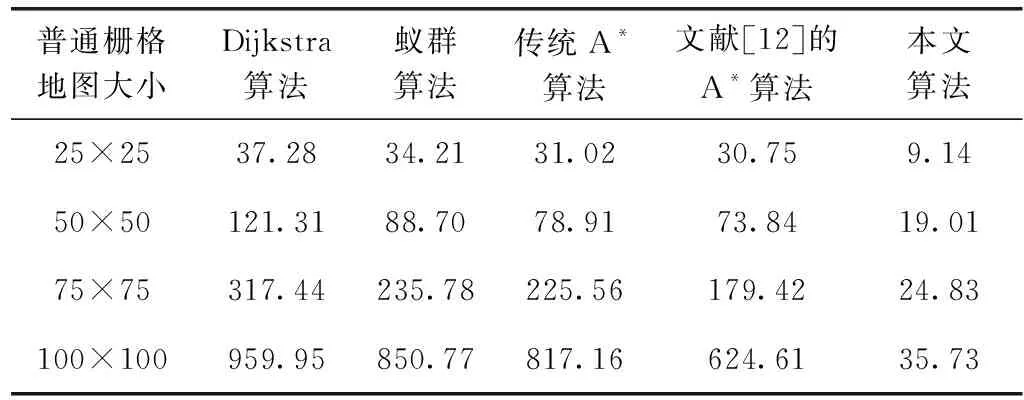
表5 不同算法搜索時間對比/ms

由上述對比結果可知：本文算法相對于Dijkstra算法、蟻群算法、傳統A*算法和文獻[12]改進A*算法均能尋找到最短路徑，而且本文算法在遍歷節點和搜索時間上具有較高的效率，隨著柵格地圖尺寸的增加，效果更加明顯。

在轉彎次數上，Dijkstra算法、蟻群算法、傳統A*算法均存在較多次數的轉彎，而本文算法與文獻[12]算法均能夠明顯減少轉彎次數，但是本文算法遍歷節點數大大減少，搜索效率更高。

4.2 列檢環境實驗分析

本文依據某公司實際列檢環境構建20×100尺寸的柵格地圖進行模擬實驗。與傳統A*算法、文獻[12]提出的改進A*轉向算法進行比較,來驗證本文算法在列檢環境地圖中的性能。

在地圖中：

白色節點：可通行節點。

黑色節點：障礙物節點。

*節點：升降平臺節點。

斜格(#)節點：檢修軌道節點。

灰色節點：尋找最優路徑遍歷過的節點。實驗結果如圖13所示。

圖13 20×100列檢柵格地圖不同A*算法結果對比

不同算法性能在列檢環境地圖中的對比見表6。

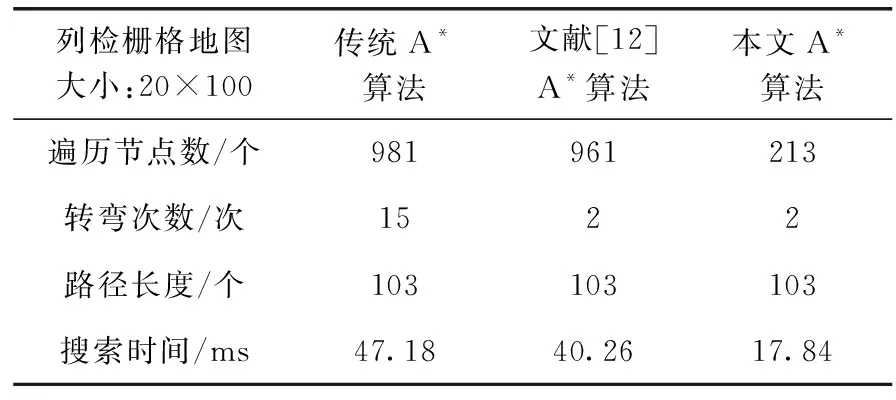
表6 不同算法性能在列檢環境地圖中的對比

由上述實驗結果可知，在列檢環境下，不同算法都能保證尋優路徑為最短路徑。但是傳統A*算法遍歷節點量大，轉彎次數較多，搜索效率低下，而文獻[12]提出的改進A*算法雖然能夠減少轉彎次數，但是對搜索效率沒有提升。本文算法能夠保證最少轉彎次數的情況下，大大減少無用節點的遍歷，提高路徑尋優效率。驗證了本文算法在列檢環境應用中的高效率性和可行性。

5 結束語

針對傳統A*算法在AGV路徑尋優過程中轉彎次數較多和遍歷節點量大的問題。本文對其進行了改進，首先，采用了轉彎懲罰機制來減少AGV路徑尋優時的轉彎次數，然后，在啟發式函數中加入“選擇因子”用于控制那些具有相同代價值的節點的選取，從而減少額外節點的遍歷，提高算法的效率。經過多組不同規格的地圖進行的仿真實驗，驗證了本文改進A*算法相對于其它路徑搜索算法提升了尋路效率并大大減少了轉彎次數。同時在仿真實驗的基礎上，實現了基于實際復雜列檢環境的AGV路徑規劃，搜索時間和規劃的路徑均能滿足列檢環境中的要求，具有一定的實際價值。在下一步的研究工作中，主要方向是能夠結合相關碰避算法實現多AGV的路徑規劃，解決動態的、復雜的多任務的調度，不斷提高算法的實際應用價值。