基于復數空間內矩陣映射的知識表示方法

田應彪，安敬民，李冠宇

(大連海事大學 信息科學技術學院，遼寧 大連 116026)

0 引 言

知識圖譜KG(knowledge graph)近年來得到了快速發展。一般以三元組 (h,r,t) 的形式表示知識圖譜中的一條事實，其中h，t代表現實世界中的兩個實體，r表示實體間存在的關系，例如(北京，位于，中國)。由于知識圖譜語義及結構的復雜性，表示學習作為關鍵解決方法，將實體與關系的語義信息表示為稠密低維實值向量，以減少實體與關系的鏈接代價[1]。近年，RotatE[2]關注表示關系模式，被證明可以表示包括對稱/反對稱、可逆、組合等多種關系模式。然而，RotatE忽略了關系模式與復雜關系的緊耦合性，并不能同時能表示實體間一對一(1-1)、一對多(1-N)、多對一(N-1)及多對多(N-N)等復雜關系以及前述幾種關系模式。如圖1為YAGO以及WordNet中部分子圖，isConnectedTo為對稱關系，同時也為一個復雜關系，其連接的首尾實體數量為一對多。hypernym與hyponym為一對逆關系，復雜關系與關系模式緊密相關。

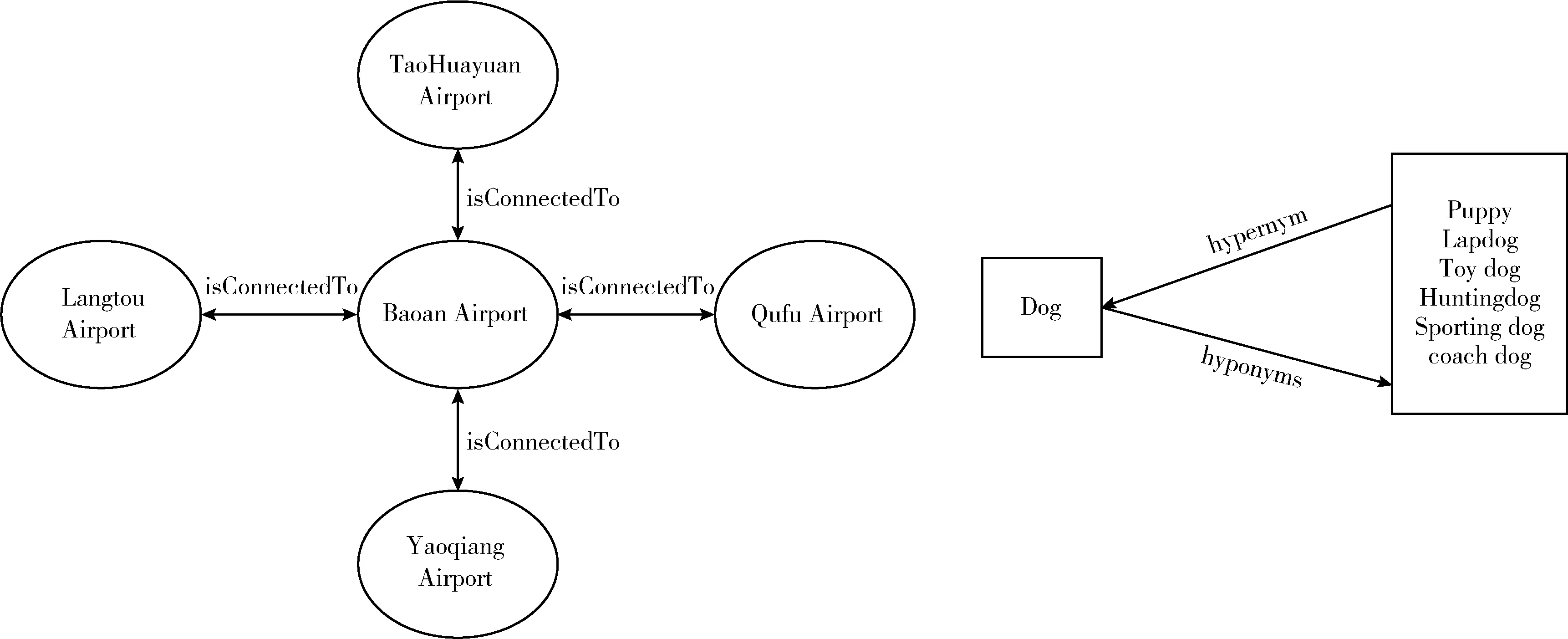
圖1 關系模式與復雜關系間的緊耦合

考慮到關系模式以及復雜關系間的緊耦合性，本文提出了MMCS(knowledge representation using matrix mapping in complex space)方法。MMCS的優勢如下：

不僅可以推斷關系模式，包括對稱模式、逆模以及組合模式，也可以建模1-N、N-1、N-N等復雜關系。與翻譯方法表示在實數空間不同，MMCS表示在復數空間，且采用適用于復數的，以向量間元素積的形式對復數實體向量每一維進行映射以解決RotatE對復雜關系建模的不足。在基于Freebase、WordNet、YAGO知識圖譜中抽取的4個通用數據集上進行鏈接預測實驗，實驗結果表明，MMCS優于大部分方法。

1 相關工作

DistMult為RESCAL的簡化版，通過限制關系矩陣為對角矩陣，達到了減少參數的目的。但是由于這種方法的特性，其只能處理對稱關系，顯然這對于一般的知識圖譜并不是十分適用[3]。HoLE[4]將實體和向量都表示在同一向量空間k。 由于循環相關運算符是不可交換的，HolE可對非對稱關系建模，但不能建模逆關系。ComplEx[5]將嵌入向量定義在復數空間，ComplEx可處理對稱、逆關系，但不能處理組合關系。

TransE將關系解釋為低維空間內實體向量間的翻譯操作，通過使頭尾實體滿足h+r≈t來捕獲三元組的結構信息[6]。TransE在1-N、N-1、N-N關系建模上效果差，TransH將實體投影到與關系相關的超平面內，以此表示前面幾種關系[7]。但TransH不能對逆關系以及組合關系建模。為建模知識圖中存在的大量關系模式，研究人員提出了RotatE，通過將關系視為頭尾實體間的旋轉操作，RotatE可以更好建模對稱關系、逆關系、組合關系[2]，但沒有考慮一對多、多對多等復雜關系。QuatE[8]使用四元數表示實體，將關系表示為四元數空間中的旋轉，但仍無法建模復雜關系。

ConvE[9]引入卷積神經網絡來表示實體以及關系向量表示。由于卷積網絡設計特性，ConvE提取局部特征的效率高，但在同一維度上的全局特征可能會丟失，影響補全性能[10]。R-GCN[11]將圖卷積神經網絡應用于處理多關系數據的鏈接預測任務。然而，R-GCN沒有考慮關系嵌入所具有的豐富語義信息，而VR-GCN[12]顯示的對關系進行嵌入并且將當前節點附近的結構信息并融入到結點表示中，之后選擇DisMult作為解碼器輸出。與圖卷積神經網絡不同的是MMCS是以單獨的解碼器的形式出現的,參數量少并可應用于圖卷積神經網絡的解碼器。

我們注意到也有一些研究人員將路徑[13,14]、實體類型[15,16]、文本和事實的聯合嵌入[17-19]、本體[20]等輔助信息引入到傳統方法中，取得了相對的提升。

相比于上述工作，本文旨在提出一種可以同時建模1-1、1-N、N-1與N-N等復雜關系以及建模對稱、逆、組合等關系模式的方法，該方法可作為其它方法的基線方法。

2 方法介紹

在這部分我們先定義了一些符號，然后在第一小節與第2小節分別介紹了3種關系模式以及復雜關系的定義，其次在第3小節中給出提出MMCS的動機，最后在第4小節中闡述了MMCS的設計細節并說明其可表示復雜關系，驗證了MMCS可建模關系模式。首先定義一些符號。本文用E表示知識圖譜中實體的集合，R表示關系的集合。知識圖譜中的三元組表示為 (h,r,t)， 其中h，r，t分別代表三元組中的頭實體、關系、尾實體，有h,t∈E,r∈R。 用黑體加粗的字母h,r,t代表他們在低維空間的向量表示，用 [h]i表示頭實體的第i維，其中i≤k。 Δ， Δ′分別代表知識圖中正確三元組集合以及錯誤三元組集合，即 (h,r,t)∈Δ表示 (h,r,t) 為正確三元組， (h,r,t)∈Δ′表示 (h,r,t) 為錯誤三元組。本文的一些符號見表1。

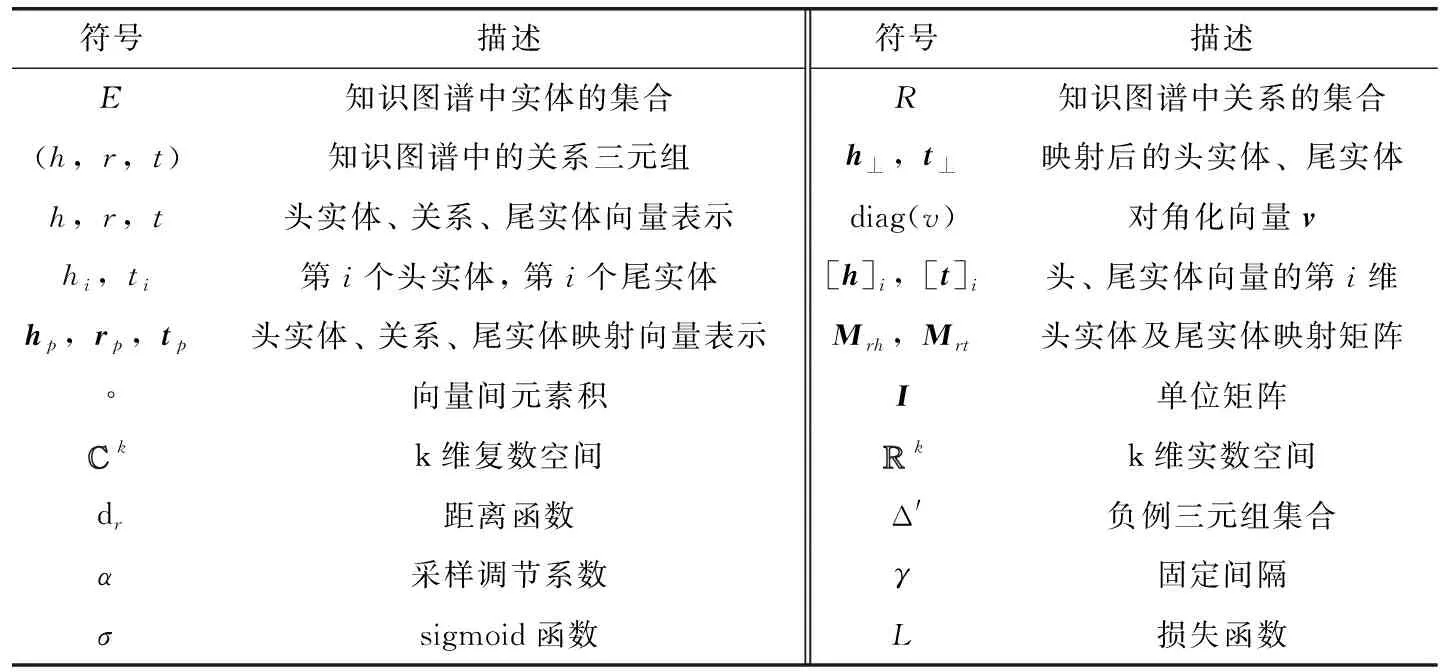
表1 重要符號及其表示

2.1 3種關系模式

知識圖中主要存在3種關系模式，即對稱、逆、組合關系。例如‘夫妻’和‘朋友’是兩組對稱關系，‘父親’

是反對稱關系，‘上位詞’的逆關系是‘下位詞’，‘父親’與‘哥哥’的組合關系是‘伯父’。3種模式的定義如下：

定義1 對稱/反對稱關系

?x,y∈E, (x,r,y)∈Δ?(y,r,x)∈Δ

(1)

?x,y∈E, (x,r,y)∈Δ?(y,r,x)∈Δ′

(2)

則稱關系r為對稱、反對稱關系。

定義2 逆關系

?x,y∈E, (x,r1,y)∈Δ?(y,r2,x)∈Δ

(3)

則稱關系r1與關系r2互為逆關系。

定義3 組合關系

?x,y,z∈E, (x,r1,y)∈ΔΛ(y,r2,z)∈
Δ?(x,r3,z)∈Δ

(4)

則稱關系r3為關系r1與r2的組合關系。

2.2 復雜關系

復雜關系可分為一對一，一對多，多對一以及多對多關系。對于每個關系r∈R， 計算r的每個頭實體對應尾實體的平均數量tphr以及每個尾實體對應頭實體的平均數量hptr。 若tphr<1.5且hptr<1.5， 則r為一對一關系；若tphr<1.5且hptr≥1.5, 則r為多對一關系；若tphr≥1.5且hptr<1.5則r為一對多關系；若tphr≥1.5且hptr≥1.5， 則r為多對多關系。

2.3 動 機

正如引言與相關工作所述的，現有的方法并不能同時表示復雜關系以及推斷對稱、逆、組合等關系模式。

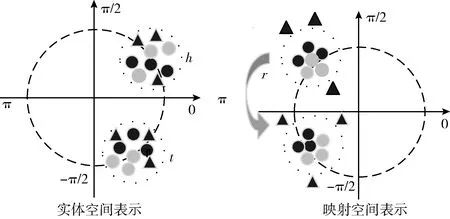
圖2 MMCS方法解釋

我們發現相同的頭(尾)實體和關系可能對應不同類型的尾(頭)實體，例如在YAGO3-10中，有10 174個頭實體滿足(?，isLocatedIn，United_States)，如圖3所示，這些實體具有不同的類型，我們認為為不同的實體設置不同的映射矩陣可以更好的建模。

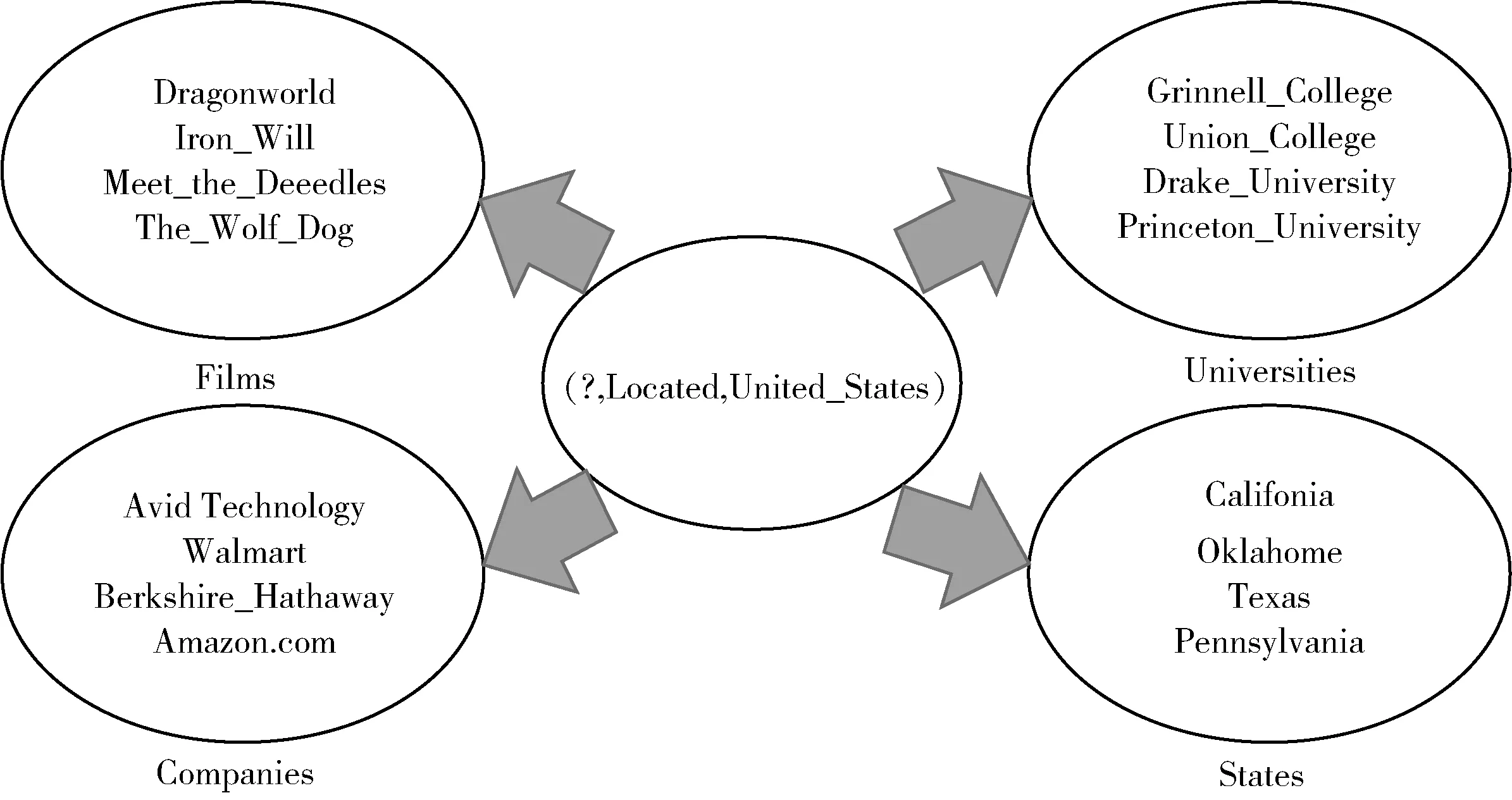
圖3 三元組(？, Located,United_States)中不同的頭實體可對應不同的類型

2.4 方法設計

在MMCS方法中，對于每個實體和關系，我們都定義兩個位于不同空間的向量，第一個用于表示實體(關系)的語義，第二個用于構造映射矩陣。所以對于任意一個三元組 (h,r,t)， 由6個向量表示，即h,r,t,hp,rp,tp， 下標p表示向量用于構造映射矩陣，其中h,r,t∈k,hp,rp,tp∈k，表示復數空間，表示實數空間，k為空間維度。我們將每個三元組的頭實體和尾實體映射到與關系及其自身相關的空間，映射矩陣的定義如下

Mrh=diag(rp°hp)+Ik×k

(5)

Mrt=diag(rp°tp)+Ik×k

(6)

其中，diag表示將向量映射為對角陣，即對于向量v，若A=diag(v)， 有Aj,j=vj； °代表向量間元素積，即 [rp°hp]j=[rp]j·[hp]j， ·表示兩數之積；I代表單位矩陣。可見頭(尾)實體的映射矩陣要受到實體和關系的共同影響。頭尾實體在映射空間的表示如下

h⊥=Mrhh

(7)

t⊥=Mrtt

(8)

其中，h⊥,t⊥∈k。 由于映射，我們期望同一關系所對應的不同的頭(尾)實體在矩陣映射后可以改變復數向量的各維模長，然后具有相同的表示，即將實體間的多對多等復雜關系轉換為一對一。然后我們定義關系r為映射得到的頭實體到尾實體間的旋轉，給定三元組 (h,r,t)， 期望t⊥=h⊥°r。 特別的，對于復數空間中的每個維度，t⊥j=h⊥jrj， 其中|rj|=1， 即為rj旋轉子，有rj=eiθ=cosθ+isinθ。 距離函數定義如下

(9)

通過將關系視為復數空間內的旋轉操作，MMCS可以建模和推斷對稱、組合、逆模式，證明如下：

證明1：MMCS可建模對稱模式： ?(x,r,y)∈Δ, (y,r,x)∈Δ， 則有

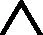
(10)

證明2：MMCS可建模逆模式： ?(x,r1,y)∈Δ, (y,r2,x)∈Δ， 若r1p=r2p， 則有

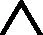
(11)

證明3：MMCS可建模組合模式： ?(x,r1,y)∈Δ, (y,r2,z)∈Δ, (x,r3,z)∈Δ若r1p=r2p=r3p， 則有

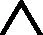
(12)

我們使用文獻[15]中的自我對抗負采樣作為損失函數，定義如下

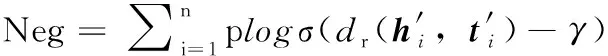
(13)

其中，γ為固定的間隔，σ為sigmoid函數， (h′i,r,t′i)∈Δ′為第i個負樣本。采樣負樣本的概率p定義如下

(14)

其中，α為采樣調節系數，α≥0。 當α=0是均勻采樣，α>0時，負樣本得分越高的權重越大。

3 實驗及分析

鏈接預測旨在根據知識圖譜中已有的事實去預測知識圖譜中缺失的實體或關系。例如，在三元組(北京，位于，？)中，尾實體‘中國’缺失。我們需要根據距離函數由低到高對知識圖譜中所有實體排名，距離越小則排名越靠前，由此獲得正確的頭體。

3.1 數據集

本文在4個常用的數據集上進行評估。這些數據集的統計見表2。

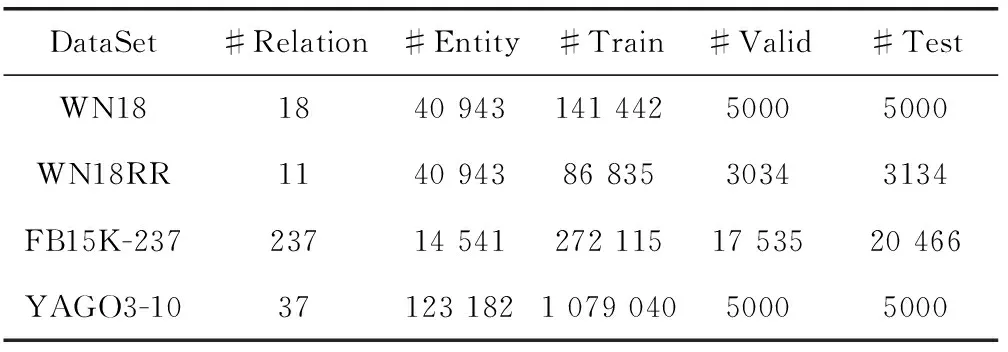
表2 4個數據集統計信息

WN18是由Border等創建的詞匯知識圖WordNet的子集。WN18中的主要關系模式為對稱和逆關系。

WN18RR是由Dettmers等篩除了反向關系模式創建的WN18數據集的子集。他們驗證了利用簡單的逆模型在WN18以及FB15K上都達到了先進的結果。其關系模式主要為對稱、組合關系。

FB15k-237是Toutanova以及Chen在發現FB15k由于存在等價和逆關系而遭受測試泄露之后構建的。他們刪除了FB15k中所有等價和逆關系，還確保訓練集中連接的實體沒有一個直接鏈接到驗證和測試集中。其關系模式主要為對稱、組合關系。

YAGO3-10也是由Dettmers等創建的，由至少各有10個關系的實體組成，包括123 182個實體和37個關系。Dettmers等用實驗驗證用逆模型在YAGO3-10測試效果很差，這意味著它不應該遭受和WN18和FB15k相同的測試泄露。

3.2 參數設置

我們使用Adam作為優化器。搜索的超參數范圍如下：向量維度K∈{200,400,500,1000}, batch大小B∈{256,512,1024}， 負樣本數量N∈{256,512,1024}， 采樣調節系數α∈{0.5,1.0,3.0}， 學習率lr∈{0.00005,0.0001,0.0002}， 軟間隔γ依據數據集不同分別調整。初始化關系向量r在0和2π間，實體及關系映射向量為1，在WN18以及WN18RR數據集上使用了正則化。最優超參數設置如下：在WN18上的最優參數為K=500，B=512，N=1024,γ=8，lr=0.0001，step=50000，25 000時下調學習率為初始學習率的1/10。在WN18RR上的最優參數為K=500，B=512，N=512，γ=4，lr=0.000 05，step=50000，25 000時下調學習率為初始學習率的1/10。在FB15k-237上的最優參數K=1000，B=512，N=256,γ=5，lr=0.000 05，step=50000，25 000時下調學習率為初始學習率的1/10。在YAGO3-10上的最優參數為K=400，B=512，N=400，γ=18，lr=0.0002，step=180000，60 000時下調學習率為初始學習率的1/5，120 000時為初始學習率的1/20。

3.3 評估指標

根據Bordes等的觀點，在測試以及驗證數據時我們用每個候選實體替換頭部實體或尾部實體以創建候選三元組。然后我們按照得分降序排列候選三元組。我們使用Bordes等的“過濾”設置，即在排名時不考慮任何現有的有效三元組。我們選用通用的平均排名(MR)，平均倒數排名(MRR)和命中次數(H@N，N∈{1,3,10}) 作為數據集的評估指標,它們的定義如式(15)～式(17)所示。其中q為測試集中單個三元組在預測頭實體或尾實體中的排名，Q為q的集合。MR表示測試集中所有三元組預測排名的平均值，MRR為排名倒數的平均值，H@N表示每個三元組預測實體時正確實體排在前N個位置的比例。MR越低，MRR越高，H@N越高代表算法預測的實體越準確，鏈接預測的結果越好

(15)

(16)

(17)

3.4 實驗結果及分析

我們將MMCS與現有的性能先進的方法進行比較，包括TransE、DistMult、ComplEx[5]、ConvE[11]、ConvKB[21]、R-GCN[11]、VR-GCN[12]、RotatE[2]。TransE、RotatE屬于幾何方法，DistMult與ComplEx屬于張量分解方法，ConvE與 ConvKB屬于卷積神經網絡方法，R-GCN與VR-GCN屬于圖卷積神經網絡方法。TransE及DisMult的結果源自文獻[2]。實驗結果見表3和表4。

從表3和表4可以看出，與其它方法相比，MMCS由于同時建模復雜關系以及多種關系模式，在數據集YAGO3-10、WN18RR和WN18上獲得最好的MR、MRR，最高的Hit@1 Hit@3和Hit@10。①在YAGO3-10數據集上MMCS 的MR比RotatE提升18%，MRR提升4.7%，H@1提升5.4%，H@3提升4.6%，H@10提升2.9%；在WN18RR數據集上MMCS的MR提升40.7%，H@3提升1.4%；在WN18數據集上MMCS的MR提升13.6%。MMCS在FB15k-237上與RotatE表現相近，我們認為是FB15k-237數據集相較其它數據集稀疏，導致映射矩陣建模效果不明顯。ConvKB屬于卷積神經網絡方法，神經網絡不可解釋。②RotatE表示能力優于TransE、DistMult、ComplEx等，其原因在于RotatE可以建模對稱、逆、組合關系模式，而TransE不能建模對稱關系，DistMult不能建模逆關系，ComplEx不能建模組合關系。

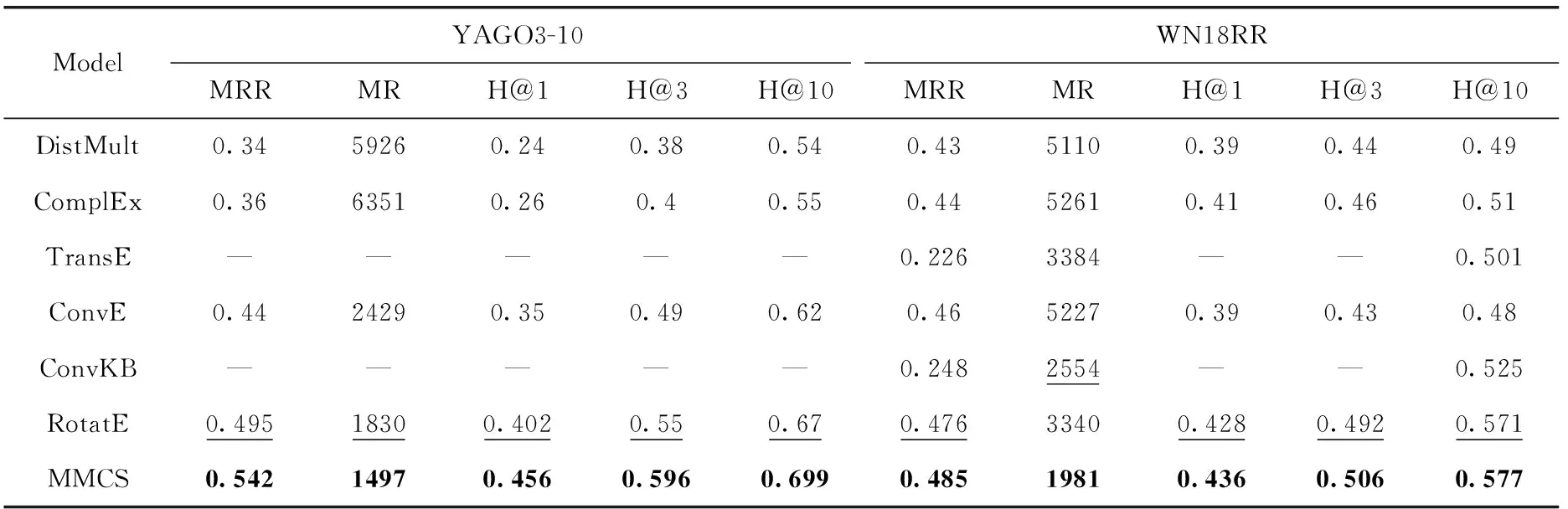
表3 YAGO3-10及WN18RR數據集上不同方法鏈接預測結果

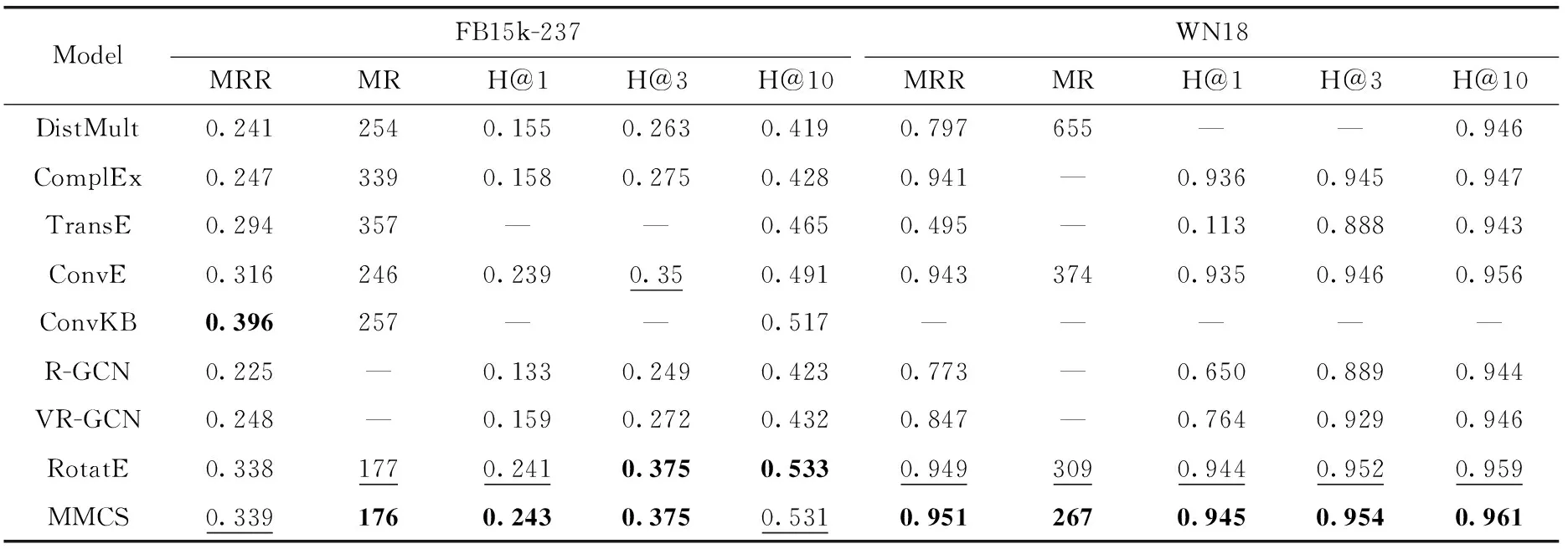
表4 FB15k-237及WN18數據集上不同方法鏈接預測結果

與RotatE相比MMCS在YAGO3-10數據集上實現了很大的提升。我們認為這是由于RotatE相比MMCS能更好地建模一對多、多對多關系模式。我們按2.2小節中復雜關系分類的方法分析了YAGO3-10中各元組所屬復雜關系的比例，表5為在測試集中的比例。可以看到YAGO3-10測試集中N-N關系所占比例很大，占85.8%。僅有0.6%的1-1關系，1-N與N-1占比13.6%。為了確認MMCS在YAGO3-10上的提升源于對復雜關系的處理能力，我們測試了MMCS在YAGO3-10上4種類別的預測頭/尾實體的MRR、Hits@1、Hits@3和Hits@10得分，見表6、表7，表中單元格左部為RotatE測試結果，右部為MMCS測試結果。RotatE與MMCS在處理1-1預測的頭部和尾部預測性能相仿。在處理1-N以及N-1預測時大部分指標相近，而在處理N-N類型的預測，MMCS表現更好，實驗結果表明MMCS更能處理復雜關系。

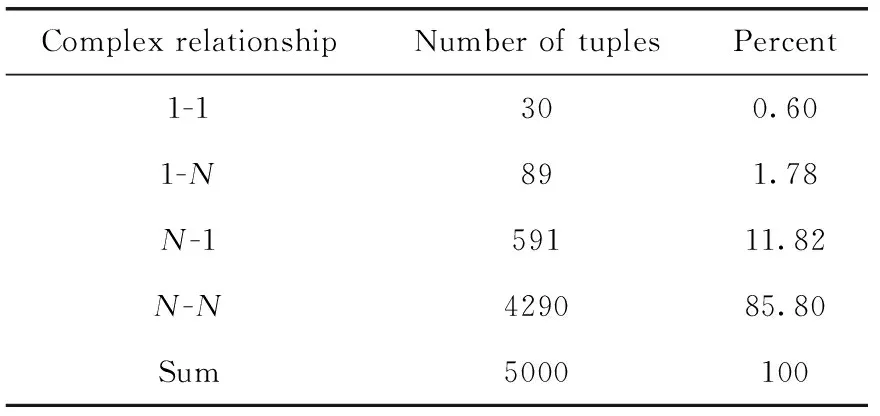
表5 YAGO3-10測試集中各元組的所屬復雜關系類別

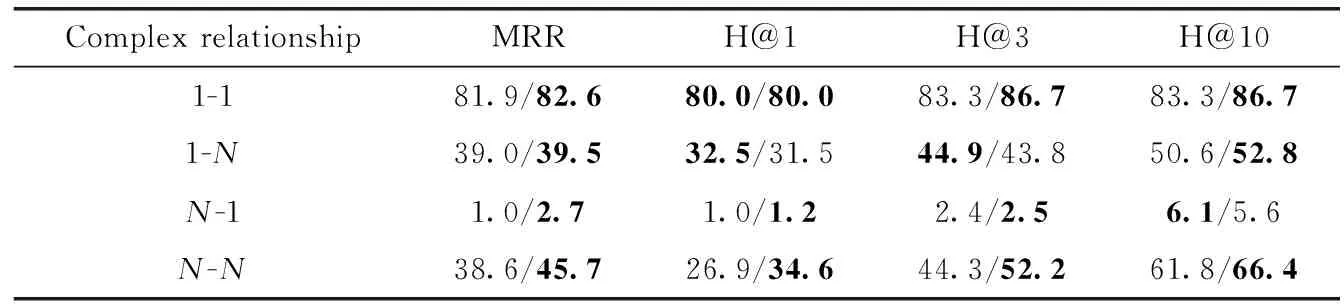
表6 RotatE與MMCS在YAGO3-10測試集上預測頭實體結果

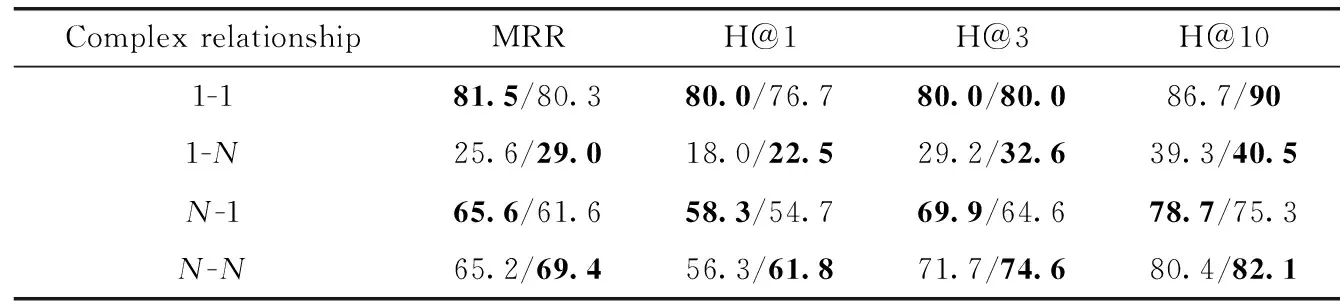
表7 RotatE與MMCS在YAGO3-10測試集上預測尾實體結果

MMCS方法中的每個關系rj有rj=eiθ=cosθj+isinθj， 為了直觀表示MMCS能隱含推理關系模式，我們忽略關系向量各維嵌入的具體位置，將關系的每一維限制到 [-π,π]， 繪制關系嵌入中每個元素的相位直方圖，橫坐標表示相位。

對稱模式：對稱模式要求對于關系r有r°r=1， 則有 [r]i=±1， 即每一維應取值于集合 {-π，0，π} 中。將WN18中訓練得到的similar_to 與verb_group關系(兩個關系均為對稱關系)每一維用直方圖統計，結果如圖4(a)、圖4(b)所示。表明MMCS可建模對稱關系模式。

逆模式：逆模式要求對于關系r1及關系r2有r1=r2-1， 即r1、r2互為共軛復數。我們將訓練后WN18中互為逆關系的hypernym與hyponym的每一維分別統計，將兩者得到的向量相加并限制其在 [-π,π] 間，得到圖4(c)，hypernym與hyponym的向量分布如圖4(d)、圖4(e)所示，可知，兩者具有很好的對稱性。相加后的向量集中在0附近。表明MMCS可建模逆關系模式。

組合模式：組合模式要求對于關系r1，r2，r3，r1°r2=r3。 我們將FB15k-237中訓練得到的3個關/award/award_nominee/award_nominations./award0/award_nomination/nominated_for(for1),/award/award_category/winners./award/aw-ard_honor/award_winner(winner),/award/award_category/nominees./award/award_nomination/nomininated_for(for2)的每一維用直方圖分別統計，如圖4(f)、圖4(g)、圖4(h)所示，將for1與winner關系相加減去for2關系得到的向量限制在 [-π,π] 間，得到圖4(i)，相加后的向量集中在0附近，表明MMCS可建模組合關系模式。

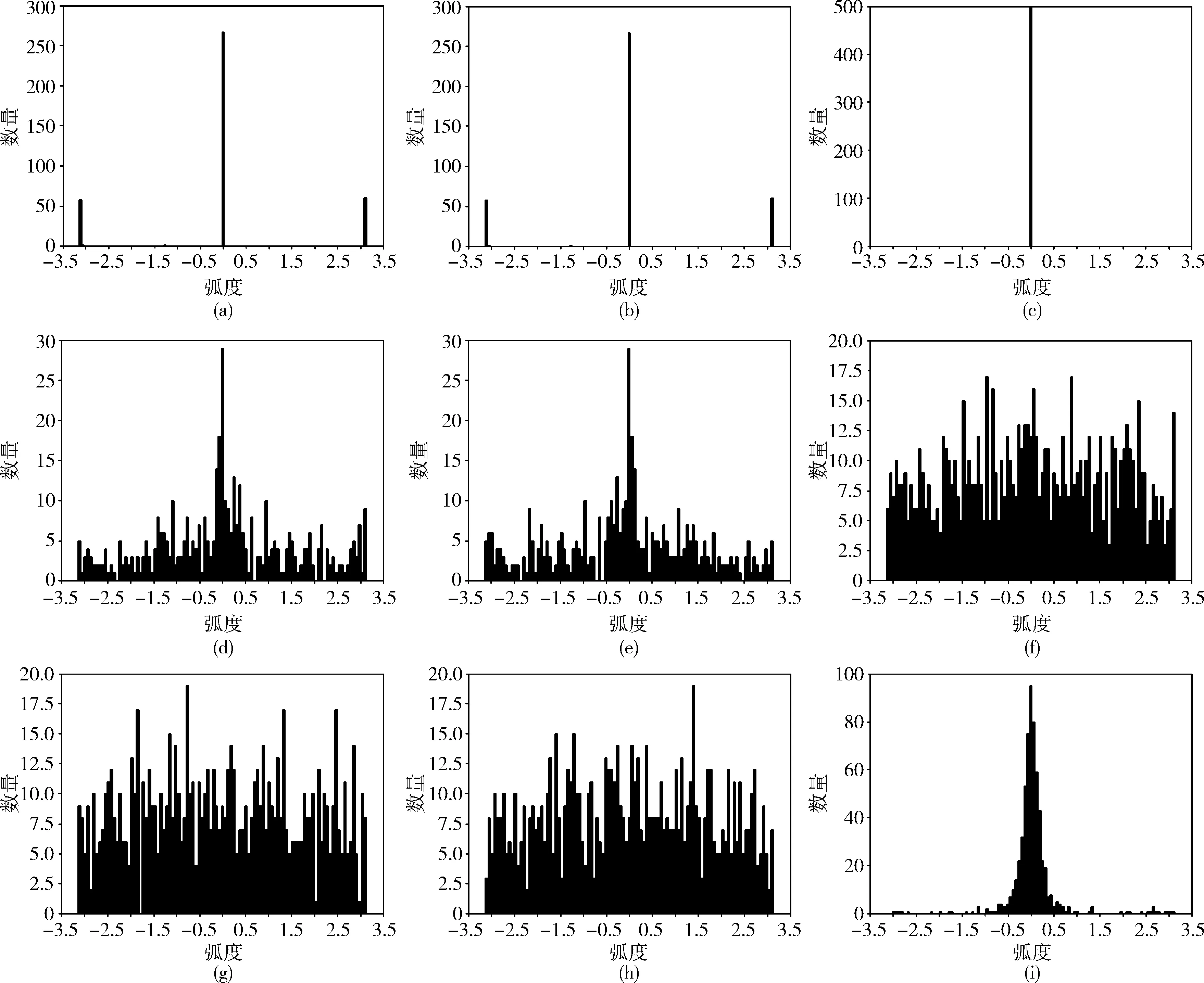
圖4 關系向量各維直方圖分布統計

4 結束語

為了同時建模1-1、1-N，N-1，N-N復雜關系以及推斷對稱、可逆、組合等關系模式，本文提出了MMCS方法，考慮到知識圖中頭(尾)實體和關系對應的尾(頭)實體的類型不同，將實體映射到不同的復數空間。在N-N關系占比最高的YAGO3-10測試集上測試，實驗結果表明MMCS對復雜關系建模更有效。我們對訓練得到的關系向量的各維數據進行統計，得到與分析相近的結果，表明MMCS能很好的建模關系模式。MMCS相比其它方法效果更好，可應用于知識圖譜補全能等相關任務中。在今后的研究中，我們考慮聯合知識圖譜本體與類型信息改進MMCS，將其引入到路徑查詢、規則挖掘等任務中。