多策略改進(jìn)的持續(xù)爆破算法
戴澤敏,曹連英
(東北林業(yè)大學(xué) 理學(xué)院,黑龍江 哈爾濱 150040)
0 引 言
持續(xù)爆破算法[1](continued explosion algorithm,CEA)是受炸彈爆破現(xiàn)象的啟發(fā)而提出的一種新型智能優(yōu)化算法。CEA算法具有原理簡單、容易實(shí)現(xiàn)等優(yōu)點(diǎn),但是和其它大部分智能優(yōu)化算法一樣,CEA算法也存在容易陷入局部最優(yōu)而導(dǎo)致早熟收斂的問題,此外,CEA在處理高維復(fù)雜優(yōu)化問題時(shí)具有尋優(yōu)能力差、尋優(yōu)結(jié)果穩(wěn)定性差等缺點(diǎn)。針對CEA存在的問題,本文提出一種基于主從結(jié)構(gòu)的階段尋優(yōu)策略,并帶有動(dòng)態(tài)爆破半徑和反向搜索變異的多策略改進(jìn)的持續(xù)爆破算法(multi-strategy improved continued explosion algorithm,MSCEA),主要改進(jìn)的工作體現(xiàn)在:①增加了初始炸點(diǎn)種群數(shù)量,由原來的單個(gè)炸點(diǎn)更改為多個(gè)炸點(diǎn)同時(shí)進(jìn)行爆破尋優(yōu)過程;②提出了一種基于主從結(jié)構(gòu)的階段尋優(yōu)策略,并設(shè)計(jì)了動(dòng)態(tài)爆破半徑,有效提高了算法的局部尋優(yōu)能力;③對算法中階段最優(yōu)解進(jìn)行反向變異來代替適應(yīng)度最差的階段最差解,以此增加種群多樣性,避免陷入局部最優(yōu);④通過位置更新策略令階段局部最優(yōu)解向階段最優(yōu)解的方向移動(dòng),提高了算法的收斂速度。
1 持續(xù)爆破算法
在持續(xù)爆破算法中,將炸彈(炸點(diǎn))及其爆破產(chǎn)生的碎片(破壞點(diǎn))所在的位置映射為目標(biāo)函數(shù)的解。炸點(diǎn)爆破產(chǎn)生破壞點(diǎn)的過程相當(dāng)于是對解的可行性空間進(jìn)行的一次探索,若某一破壞點(diǎn)的適應(yīng)度最優(yōu),則將此破壞點(diǎn)作為新炸點(diǎn)繼續(xù)爆破尋優(yōu),若炸點(diǎn)的適應(yīng)度最優(yōu),則擴(kuò)大爆破半徑繼續(xù)生成新的破壞點(diǎn)。持續(xù)爆破算法通過更換炸點(diǎn)以及擴(kuò)大炸點(diǎn)爆破半徑等操作實(shí)現(xiàn)尋優(yōu)過程。
定義目標(biāo)函數(shù)f(x), 最大爆破代數(shù)Maxgen,代數(shù)疊加器gen,炸點(diǎn)x的范圍(上界v,下界u),目標(biāo)函數(shù)最優(yōu)值M,半徑擴(kuò)大次數(shù)r,半徑擴(kuò)大次數(shù)上限Maxr,爆破半徑Re,空間維度D,炸點(diǎn)爆破時(shí)產(chǎn)生的破壞點(diǎn)數(shù)量為q,每次爆破半徑變化大小為Rchange(下文若出現(xiàn)相同符號,表示含義相同)。
持續(xù)爆破算法的具體實(shí)現(xiàn)步驟如下:
步驟1 在給定的D維解空間范圍內(nèi)隨機(jī)生成一個(gè)初始炸點(diǎn)x。
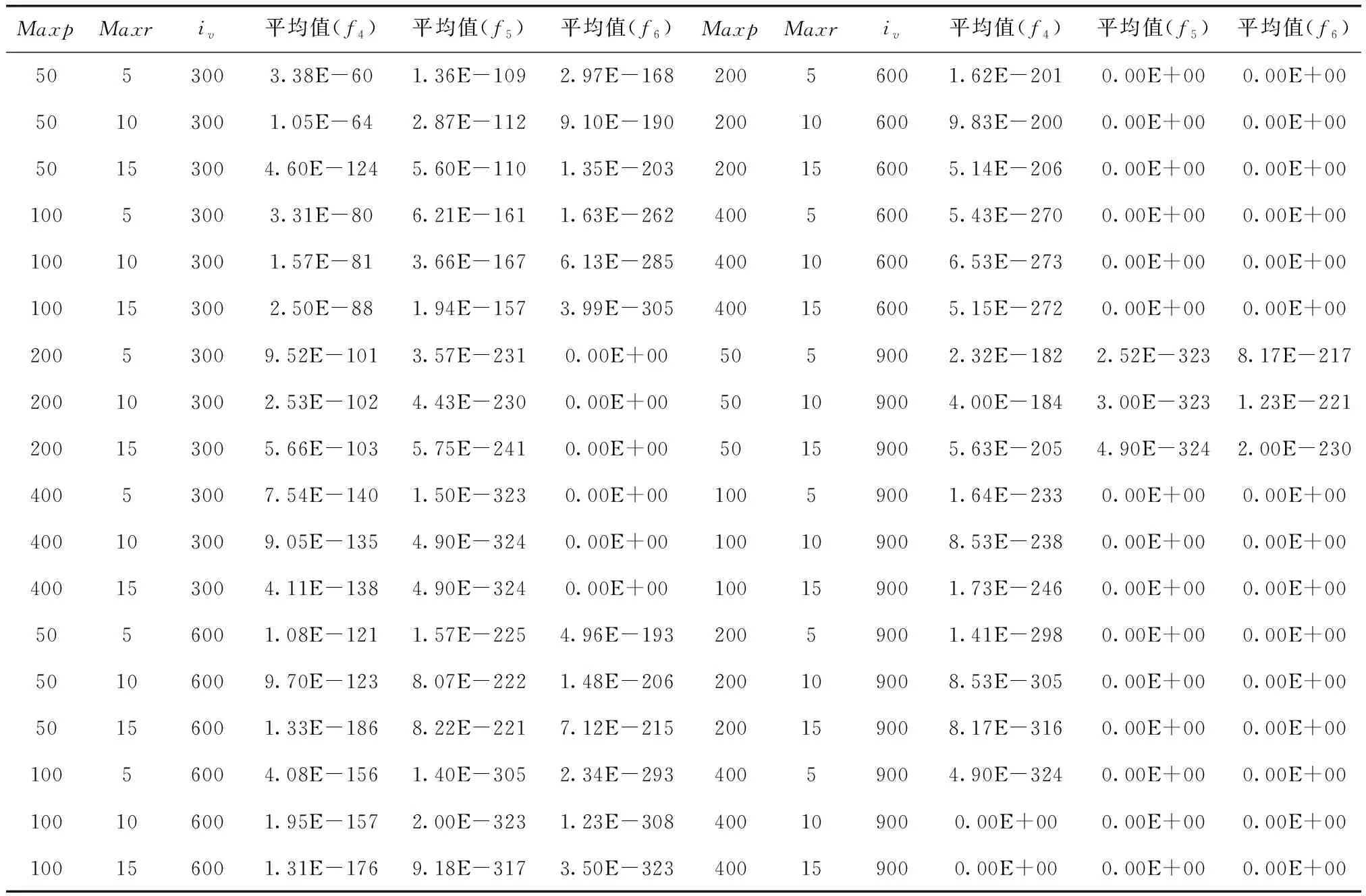
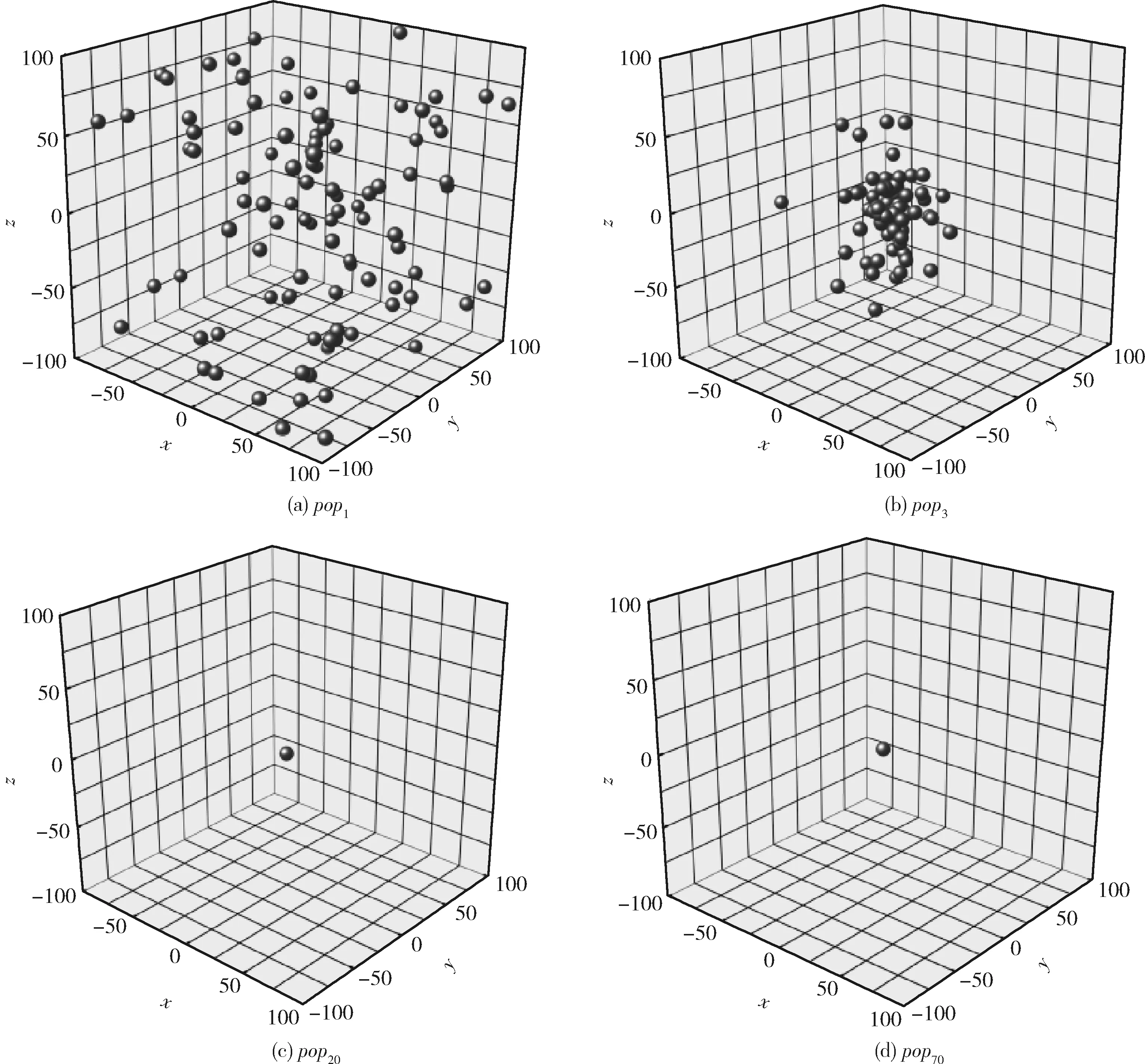
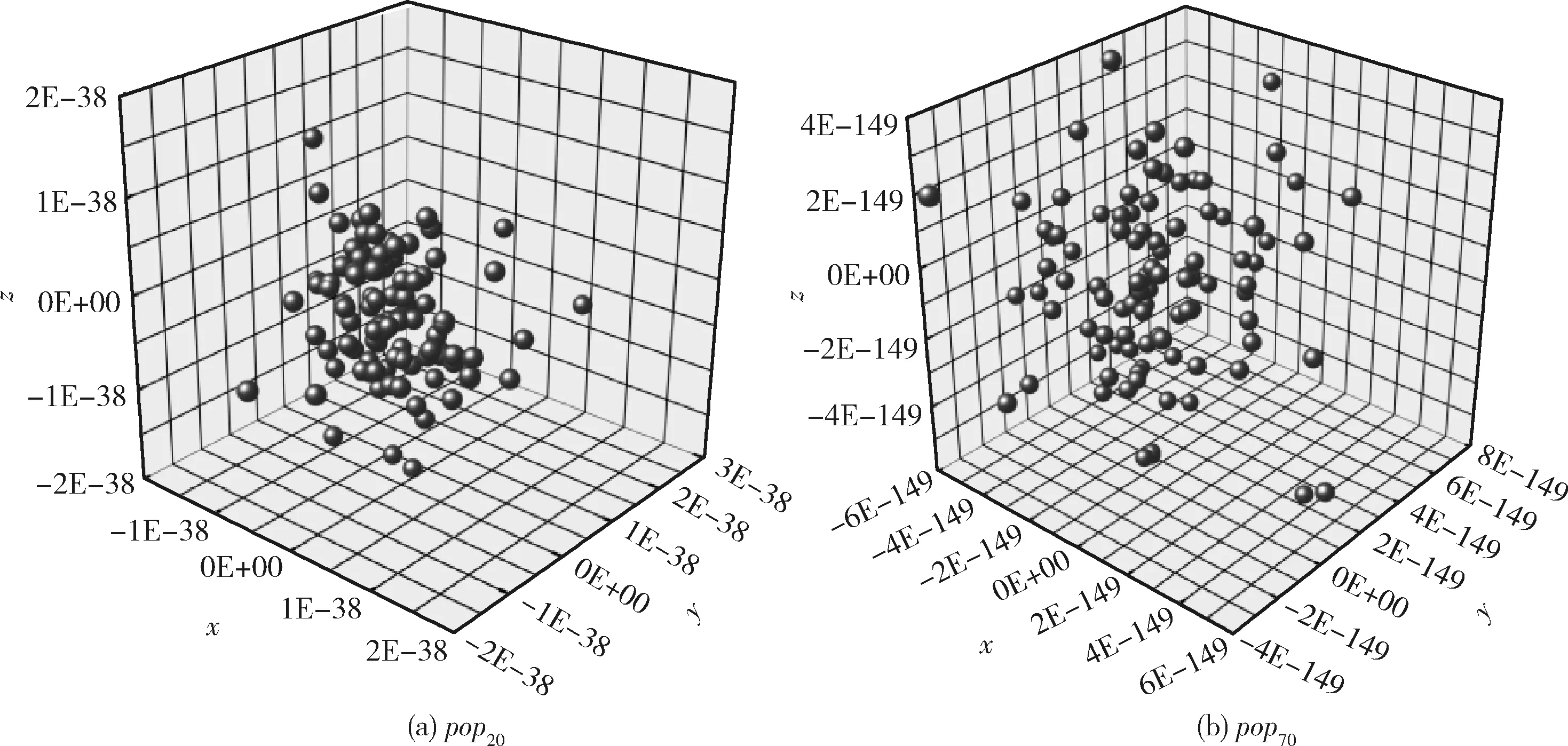
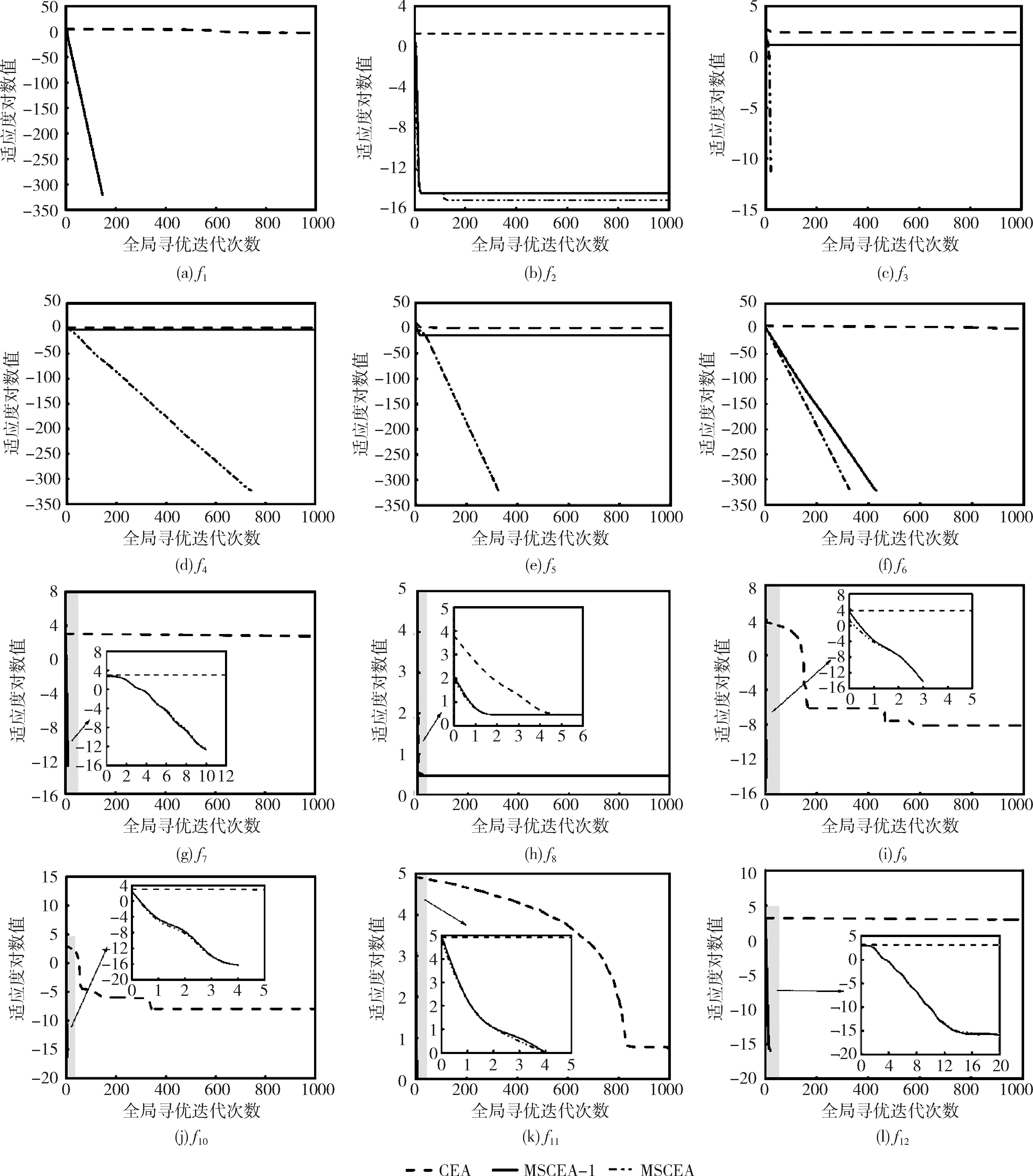
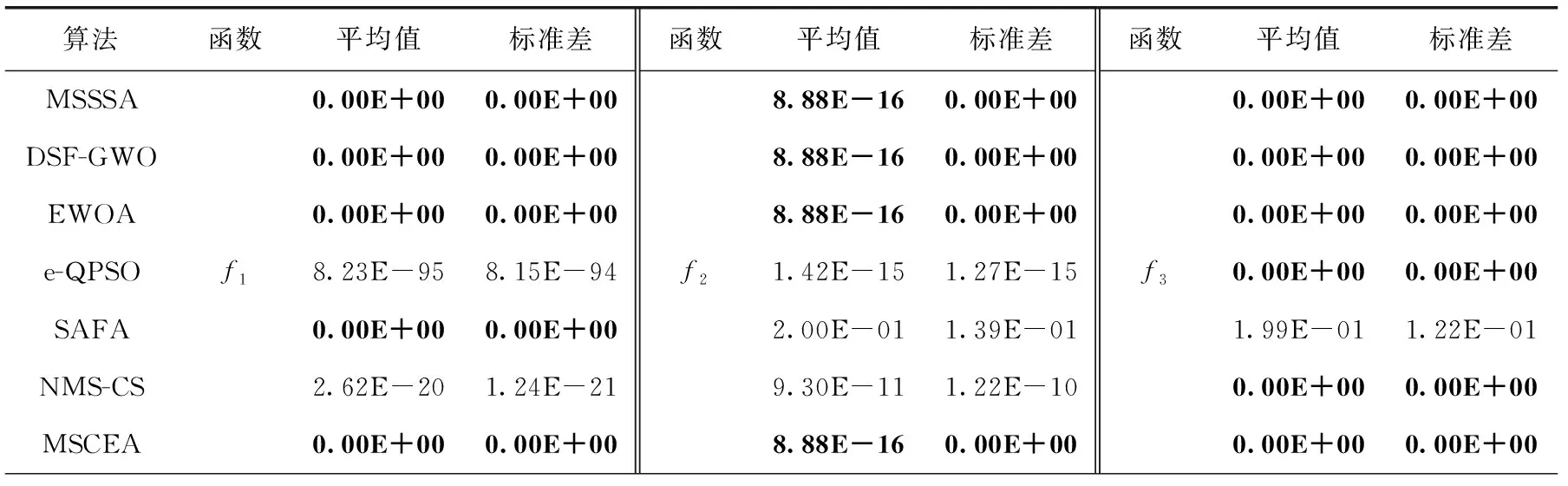
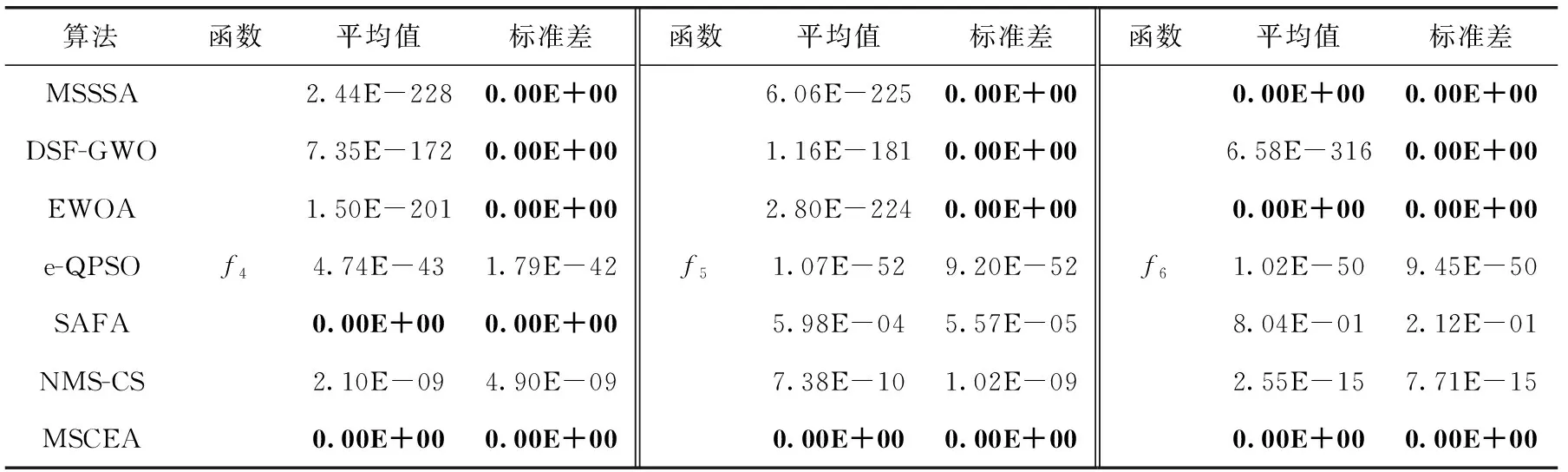
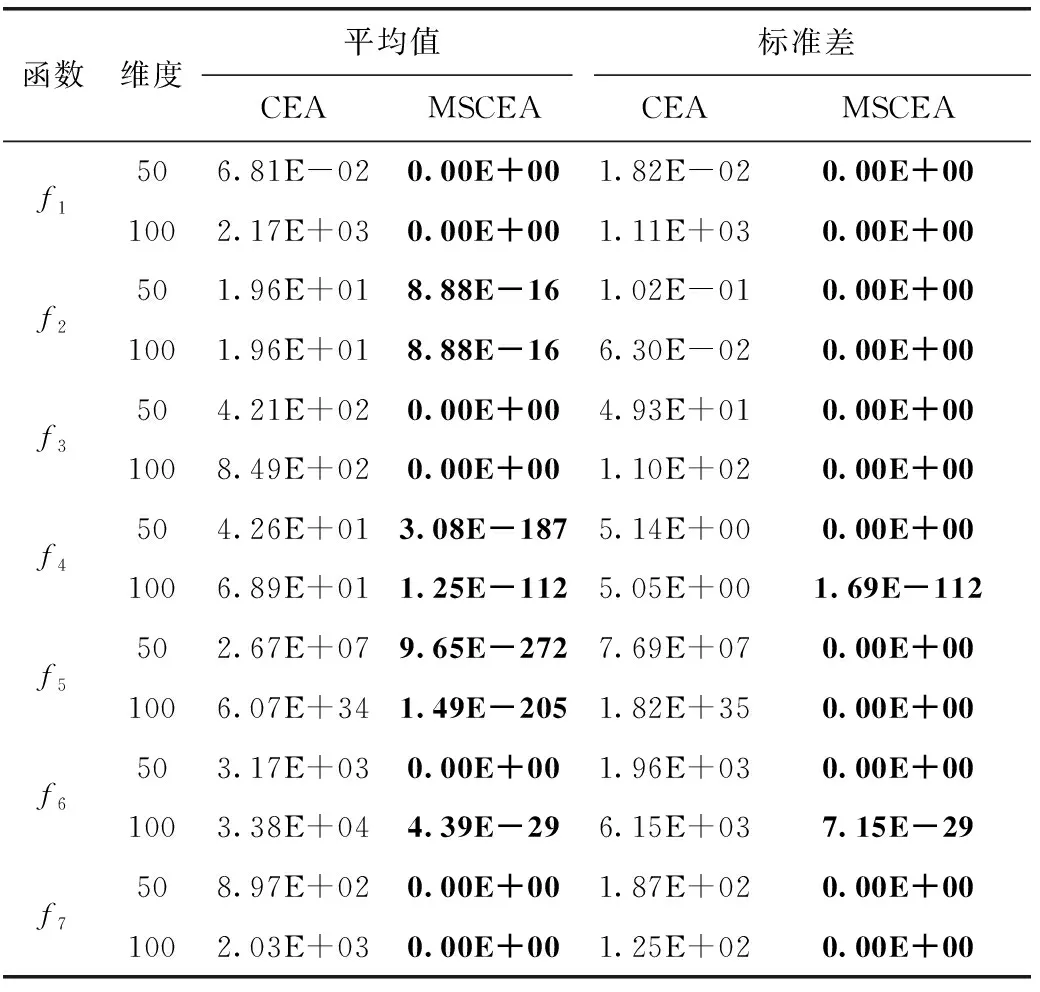
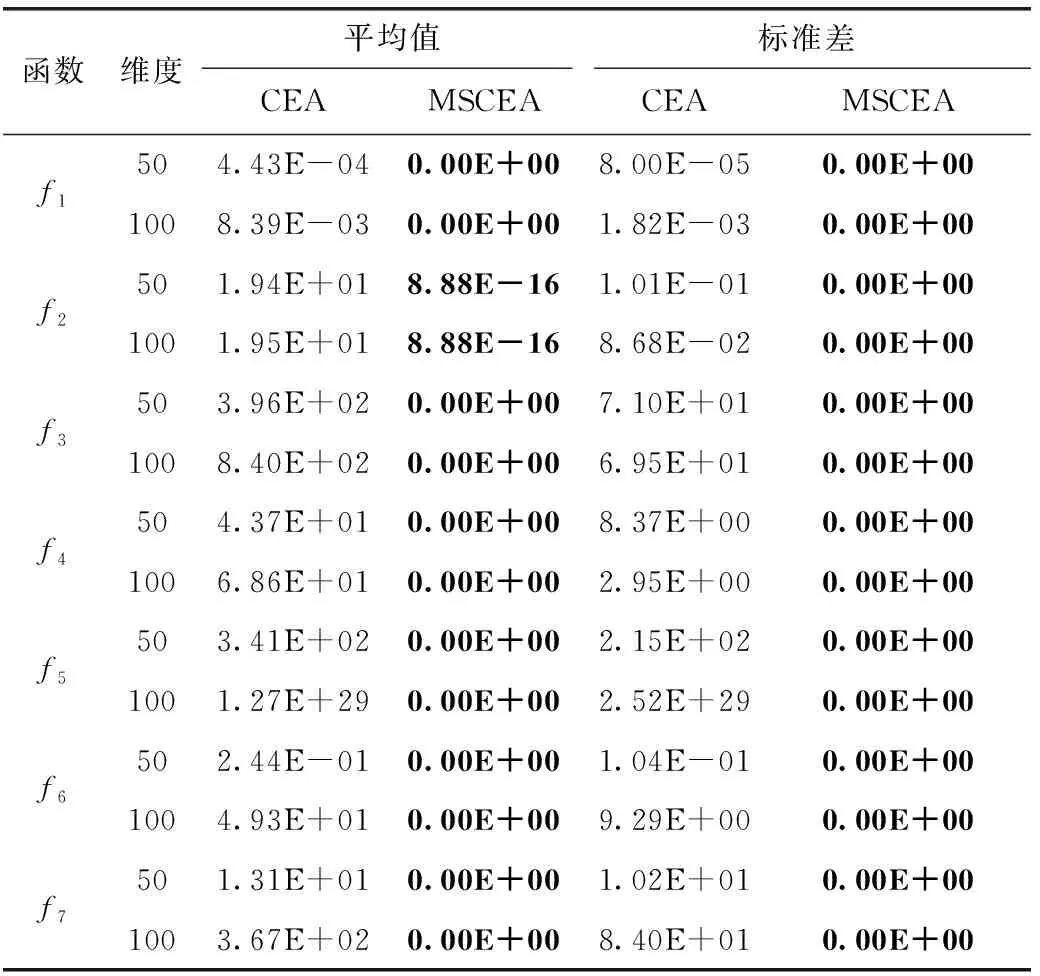
步驟2 若滿足gen Re=rand (1) 其中,rand為(0,1)范圍內(nèi)的隨機(jī)數(shù)。 步驟3 隨機(jī)生成q個(gè)爆破方向,并根據(jù)爆破半徑生成q個(gè)破壞點(diǎn),比較炸點(diǎn)和q個(gè)破壞點(diǎn)的適應(yīng)度。若某一破壞點(diǎn)的適應(yīng)度最優(yōu),則將此破壞點(diǎn)作為新炸點(diǎn),執(zhí)行步驟5;若炸點(diǎn)的適應(yīng)度最優(yōu),說明沒有找到優(yōu)于炸點(diǎn)的破壞點(diǎn),半徑擴(kuò)大次數(shù)r加1,執(zhí)行步驟4。 步驟4 若滿足r Re=Re+Rchange×r (2) x′=x+2×Re×I (3) 步驟5 代數(shù)疊加器gen加1,執(zhí)行步驟2。 步驟6 當(dāng)gen=Maxgen時(shí),終止程序,同時(shí)輸出當(dāng)前適應(yīng)度最優(yōu)的值作為目標(biāo)函數(shù)最優(yōu)值。 持續(xù)爆破算法的不足可概括為4點(diǎn):①初始炸點(diǎn)種群的多樣性較低,對于多峰優(yōu)化問題,單一炸點(diǎn)的爆破尋優(yōu)過程容易導(dǎo)致算法陷入局部最優(yōu);②強(qiáng)制遷移炸點(diǎn)位置的變異方式容易使適應(yīng)度較優(yōu)的炸點(diǎn)丟失,導(dǎo)致算法的收斂能力較弱;③在CEA中,只有在未找到適應(yīng)度優(yōu)于炸點(diǎn)的破壞點(diǎn)時(shí)擴(kuò)大半徑搜索,沒有實(shí)現(xiàn)爆破半徑的動(dòng)態(tài)變化,導(dǎo)致算法局部搜索能力較弱,搜索精度較低。 在“雇主/工人”[2]的主從式結(jié)構(gòu)中,多個(gè)工人(子群)同時(shí)進(jìn)行獨(dú)立作業(yè),并將信息反饋給雇主。雇主將信息整合分析,選取有用信息再傳遞給所有工人,以此提高工作效率,故本文將此結(jié)構(gòu)融入CEA算法中。將CEA中單一炸點(diǎn)的爆破過程更改為n個(gè)炸點(diǎn)同時(shí)且獨(dú)立完成imax次階段尋優(yōu)過程,其中每次階段尋優(yōu)過程都包括一次階段局部尋優(yōu)和一次階段全局尋優(yōu)過程。 第i次階段全局尋優(yōu)過程(雇主作業(yè)):將pbest(i)中適應(yīng)度最優(yōu)的解記為第i次階段最優(yōu)解gbesti,適應(yīng)度最差的解記為第i次階段最差解gworsti。 將imax次階段尋優(yōu)過程視為全局尋優(yōu)過程,并將imax視為全局尋優(yōu)迭代次數(shù),將得到的gbestimax作為全局最優(yōu)解。 在持續(xù)爆破算法中,炸點(diǎn)的爆破半徑直接影響算法的尋優(yōu)效率,半徑過大會(huì)導(dǎo)致算法局部尋優(yōu)能力差,尋優(yōu)精度低,而半徑過小又會(huì)導(dǎo)致算法跳出局部收斂的能力差。因此,針對每個(gè)炸點(diǎn)所進(jìn)行的階段局部尋優(yōu)過程,設(shè)計(jì)了動(dòng)態(tài)爆破半徑。 當(dāng)某一破壞點(diǎn)適應(yīng)度優(yōu)于炸點(diǎn)時(shí),新的爆破半徑公式如下 (4) 當(dāng)炸點(diǎn)適應(yīng)度優(yōu)于破壞點(diǎn)時(shí),新的爆破半徑公式如下 (5) 此時(shí)p的值固定,搜索半徑Re隨著半徑擴(kuò)大次數(shù)r的增加而擴(kuò)大,以此來繼續(xù)尋找優(yōu)于炸點(diǎn)的破壞點(diǎn),實(shí)現(xiàn)了半徑的動(dòng)態(tài)變化,有效提高了算法的局部尋優(yōu)能力。 反向?qū)W習(xí)策略被廣泛應(yīng)用于最優(yōu)化問題[3-6],其中心思想在于在優(yōu)化算法中,基于當(dāng)前的最優(yōu)解,同時(shí)評估其反向?qū)W習(xí)的解的適應(yīng)度,擇優(yōu)進(jìn)行選擇。 定義1 若s=(s1,s2,…,sD) 為D維空間中的一個(gè)點(diǎn),其中sh∈(uh,vh), 則根據(jù)式(6)定義s進(jìn)行反向?qū)W習(xí)的解為s′ (6) 可以看出,根據(jù)反向?qū)W習(xí)策略生成的可行解相當(dāng)于是對對稱空間進(jìn)行的一次搜索,有效擴(kuò)大了搜索空間,增加了跳出局部最優(yōu)的可能性,故本文將反向?qū)W習(xí)機(jī)制融入到CEA算法中。 在前期的階段尋優(yōu)過程中,通過式(7)和式(8)將gbesti進(jìn)行反向變異后得到gbesti(*) 來代替gworsti gbesti(*)=u+v-gbesti (7) (8) 其中,iv表示全局尋優(yōu)過程中的變異次數(shù)上限,如此既舍棄了表現(xiàn)較差的gworsti,也擴(kuò)大了搜索空間,增強(qiáng)了算法跳出局部最優(yōu)的能力。在后期的階段尋優(yōu)過程中,為提高收斂速度,不再進(jìn)行反向搜索變異,以免算法收斂速度過慢影響尋優(yōu)效率。 第i次階段尋優(yōu)結(jié)束之后,階段局部最優(yōu)解通過下述方式向階段最優(yōu)解的方向移動(dòng),產(chǎn)生第i+1次階段尋優(yōu)過程的初始炸點(diǎn)種群,以此實(shí)現(xiàn)種群之間信息的有效交互,平衡算法的局部搜索能力和全局搜索能力,提高了收斂速度和尋優(yōu)效率。 (9) 圖1描述了當(dāng)i 圖1 i 圖2描述了當(dāng)i≥iv時(shí)炸點(diǎn)的位置更新過程,依舊設(shè)二維搜索空間中第i次階段尋優(yōu)過程開始時(shí)有6個(gè)初始炸點(diǎn),通過第i次階段局部尋優(yōu)過程得到了A-F這6個(gè)第i次階段局部最優(yōu)解,圖2(b)表示找出A-F中適應(yīng)度最優(yōu)的B作為第i次階段最優(yōu)解,圖2(c)表示A、C-F分別通過式(9) 向B移動(dòng)得到A’、C’-F’。最后,將A’、C’-F’、B作為第i+1次階段尋優(yōu)過程開始時(shí)的6個(gè)初始炸點(diǎn)。 圖2 i≥iv時(shí)炸點(diǎn)的位置更新 步驟1 初始化各個(gè)參數(shù),隨機(jī)生成n個(gè)炸點(diǎn)作為第1次階段尋優(yōu)過程的初始炸點(diǎn)種群pop1。 步驟2 若滿足i≤imax,則令p=1,n個(gè)炸點(diǎn)獨(dú)立進(jìn)行階段局部尋優(yōu)過程,分別執(zhí)行步驟3~步驟8;否則轉(zhuǎn)至步驟12。 步驟3 若滿足p≤Maxp,則令r=1,根據(jù)式(4)生成爆破半徑Re;否則轉(zhuǎn)至步驟8。 步驟4 隨機(jī)生成q個(gè)爆破方向,并根據(jù)爆破半徑生成q個(gè)破壞點(diǎn)。 步驟5 根據(jù)目標(biāo)函數(shù)計(jì)算并比較炸點(diǎn)和q個(gè)破壞點(diǎn)處的適應(yīng)度,若某一破壞點(diǎn)的適應(yīng)度最優(yōu),則將此破壞點(diǎn)作為新炸點(diǎn)并轉(zhuǎn)至步驟7;若炸點(diǎn)的適應(yīng)度最優(yōu),說明沒有找到優(yōu)于炸點(diǎn)的破壞點(diǎn),執(zhí)行步驟6。 步驟6 若滿足r≤Maxr,則根據(jù)式(5)擴(kuò)大爆破半徑,r=r+1,轉(zhuǎn)至步驟4;否則執(zhí)行步驟7。 步驟7p=p+1,返回步驟3。 步驟9 當(dāng)n個(gè)炸點(diǎn)全部完成步驟3~步驟8時(shí),會(huì)得到一個(gè)階段局部最優(yōu)解集pbest(i)、階段最優(yōu)解gbesti和階段最差解gworsti。 步驟10 判斷是否滿足i 步驟11i=i+1,轉(zhuǎn)至步驟2。 步驟12 輸出當(dāng)前階段最優(yōu)解作為全局最優(yōu)解。 本文仿真實(shí)驗(yàn)環(huán)境:64位Windows 10操作系統(tǒng),處理器為Intel(R) Xeon(R) Gold 6242R CPU @3.10 GHz 3.09 GHz(2處理器),內(nèi)存為256 GB,編程軟件為MATLAB R2019b。 為了驗(yàn)證算法的可行性和優(yōu)越性,本文采用表1中的函數(shù)作為測試函數(shù),既包括檢驗(yàn)算法尋優(yōu)精度的單峰函數(shù),也有檢驗(yàn)算法避免早熟收斂、跳出局部最優(yōu)能力的多峰函數(shù)。 表1 測試函數(shù) 本文算法的基本參數(shù)設(shè)置如下:每次階段尋優(yōu)的初始炸點(diǎn)種群數(shù)量n=10,每個(gè)炸點(diǎn)單次爆破生成的破壞點(diǎn)數(shù)量q=5,函數(shù)f1~f7的維數(shù)D=30,全局尋優(yōu)迭代次數(shù)imax=1000。 以較難尋得最優(yōu)解的f4~f6函數(shù)為例,表2給出了隨著Maxp、Maxr和iv的變化,函數(shù)f4~f6的部分尋優(yōu)結(jié)果。由于iv是全局尋優(yōu)過程中的變異次數(shù)上限,變異次數(shù)過少會(huì)造成算法跳出局部最優(yōu)的能力不足,容易導(dǎo)致早熟收斂,而次數(shù)過多會(huì)導(dǎo)致算法后期收斂速度緩慢,降低尋優(yōu)效率,所以設(shè)置全局尋優(yōu)迭代次數(shù)imax的30%、60%、90%,即300、600、900作為iv的取值進(jìn)行仿真實(shí)驗(yàn),取10次實(shí)驗(yàn)結(jié)果的平均值與標(biāo)準(zhǔn)差。經(jīng)過多次實(shí)驗(yàn)并且綜合考慮所有測試函數(shù)的尋優(yōu)效果,將迭代參數(shù)設(shè)置如下:Maxp=400,Maxr=10,iv=imax×90%。 表2 Maxp、Maxr、iv不同取值下的實(shí)驗(yàn)結(jié)果對比 3.4.1 與CEA對比 為充分說明MSCEA的可行性與有效性,在表3中將其與原始持續(xù)爆破算法(CEA)進(jìn)行比較。CEA算法參數(shù)設(shè)置:將Maxgen視為全局尋優(yōu)迭代次數(shù),同樣取Maxgen=1000,其它參數(shù)設(shè)置與原文獻(xiàn)保持一致。因?yàn)镃EA中的初始炸點(diǎn)和MSCEA中第一次階段尋優(yōu)的初始炸點(diǎn)種群pop1均為隨機(jī)生成,為了降低算法結(jié)果的偶然性,對每個(gè)測試函數(shù)都獨(dú)立進(jìn)行20次仿真實(shí)驗(yàn)后記錄平均值和標(biāo)準(zhǔn)差,并將算法中最好的尋優(yōu)結(jié)果加粗表示。 表3 CEA與MSCEA的實(shí)驗(yàn)結(jié)果對比 通過表3可以看出,對于函數(shù)f8,CEA和MSCEA均能尋得最優(yōu)值,說明MSCEA和CEA均具備尋找到不為0的最優(yōu)值的能力;對于其它測試函數(shù),多策略改進(jìn)后的持續(xù)爆破算法的尋優(yōu)結(jié)果均優(yōu)于持續(xù)爆破算法。相比于CEA,MSCEA的尋優(yōu)精度大幅度提高,除函數(shù)f2外,均能找到測試函數(shù)的理論最優(yōu)值。雖然MSCEA無法找到函數(shù)f2的理論最優(yōu)值,但是與CEA算法相比,尋優(yōu)精度提高了16個(gè)數(shù)量級。對于最優(yōu)解不在原點(diǎn)的f8、f11和f12函數(shù),MSCEA也能找到理論最優(yōu)值,說明MSCEA不存在易在原點(diǎn)或原點(diǎn)附近尋優(yōu)的缺陷。同時(shí)從表3中的標(biāo)準(zhǔn)差可知,MSCEA算法在函數(shù)f1~f12上得到的標(biāo)準(zhǔn)差都為0,說明MSCEA算法具有較強(qiáng)的魯棒性。綜合分析說明MSCEA算法具有較強(qiáng)的搜索能力,表現(xiàn)出良好的尋優(yōu)性能。 為對種群多樣性進(jìn)行分析,圖3展示了f1函數(shù)在D=3,n=100時(shí)不同次階段尋優(yōu)時(shí)初始炸點(diǎn)的分布情況,其中popi表示第i次階段尋優(yōu)過程的初始炸點(diǎn)種群,因?yàn)榫S數(shù)較低,炸點(diǎn)能很快靠近理論最優(yōu)解,驗(yàn)證了MSCEA算法的可行性。通過圖4給出的初始炸點(diǎn)種群pop20和pop70的局部放大圖可以看出,隨著階段尋優(yōu)次數(shù)的增加,炸點(diǎn)在尋優(yōu)精度越來越高的同時(shí)仍然在一定范圍內(nèi)保持著較高的種群多樣性,說明由階段局部最優(yōu)解向階段最優(yōu)解移動(dòng)的種群更新策略能夠?qū)尚薪饪臻g進(jìn)行更加細(xì)致的搜索,有效平衡了算法的局部開發(fā)和全局勘探能力,提高了算法的尋優(yōu)精度。 圖3 炸點(diǎn)分布 圖4 局部放大圖 為更直接地了解改進(jìn)算法的收斂速度和探究反向搜索變異策略對尋優(yōu)效果的影響,圖5給出了CEA、MSCEA-1、MSCEA在測試函數(shù)上的迭代收斂曲線圖,其中MSCEA-1算法為MSCEA算法去掉對階段最優(yōu)解的反向變異操作。為方便觀察,對得到的適應(yīng)度值取以10為底的對數(shù)。從圖5可以看出,對于函數(shù)f1、f7~f12,MSCEA-1和MSCEA的收斂曲線基本重合,收斂速度和尋優(yōu)精度相比于CEA均大幅度提高,這表明反向變異策略對這些函數(shù)尋優(yōu)結(jié)果的影響較小,說明主從結(jié)構(gòu)的階段尋優(yōu)策略的有效性,平衡了算法的局部開發(fā)和全局勘探能力,動(dòng)態(tài)尋優(yōu)半徑能大幅度提高尋優(yōu)精度。而對于函數(shù)f3~f5,CEA和MSCEA-1在迭代前期均會(huì)陷入局部最優(yōu),表明反向搜索變異策略擴(kuò)大了搜索空間,能夠有效加強(qiáng)算法跳出局部最優(yōu)的能力。對于函數(shù)f2和f6,MSCEA-1和MSCEA的尋優(yōu)精度明顯提高,也能快速達(dá)到收斂狀態(tài),并且從圖中可以看出,加入反向變異策略的MSCEA算法尋優(yōu)精度更高,收斂速度更快,說明反向變異策略能夠避免早熟收斂。 圖5 測試函數(shù)的收斂曲線 3.4.2 與其它算法對比 為進(jìn)一步體現(xiàn)MSCEA算法的尋優(yōu)性能,將其與混合策略改進(jìn)的麻雀搜索算法(MSSSA)[7]、基于翻筋斗覓食策略的灰狼優(yōu)化算法(DSF-GWO)[8]、一種用于全局優(yōu)化的增強(qiáng)型鯨魚優(yōu)化算法(EWOA)[9]、一種改進(jìn)的量子粒子群優(yōu)化算法(e-QPSO)[10]、基于自適應(yīng)策略的螢火蟲算法(SAFA)[11]、一種改進(jìn)的布谷鳥搜索算法(NMS-CS)[12]進(jìn)行比較。由于不同類型優(yōu)化算法的機(jī)制不同,所以本文直接引用了參考文獻(xiàn)[7-12]中所給出的相同維數(shù)下的數(shù)據(jù)結(jié)果進(jìn)行比較,并將算法中最好的尋優(yōu)結(jié)果加粗表示,MSCEA算法的實(shí)驗(yàn)參數(shù)設(shè)置與3.3節(jié)一致,數(shù)據(jù)對比見表4。 表4 相同維度下的不同算法的尋優(yōu)結(jié)果對比 表4(續(xù)) 根據(jù)表4中給出的數(shù)據(jù)可以直觀地看出不同算法對于函數(shù)的尋優(yōu)效果不同,只有MSCEA能找到函數(shù)f5的最優(yōu)值,說明MSCEA有能力避免早熟收斂,有效解決函數(shù)優(yōu)化問題。此外,只有MSCEA在6個(gè)函數(shù)上的尋優(yōu)結(jié)果均為最優(yōu),說明MSCEA具有較為出色的尋優(yōu)表現(xiàn),在優(yōu)化算法中具有較強(qiáng)的競爭力。 為驗(yàn)證MSCEA在高維下的尋優(yōu)性能,表5給出了CEA和MSCEA在高維(50、100維)函數(shù)優(yōu)化中的平均值和標(biāo)準(zhǔn)差,算法的實(shí)驗(yàn)參數(shù)設(shè)置與3.3節(jié)和3.4.1節(jié)一致。從表5可以看出,在高維情況下,MSCEA算法仍能尋得部分函數(shù)的理論最優(yōu)值。對于其余部分函數(shù),MSCEA算法雖然沒能找到理論最優(yōu)值,但尋優(yōu)精度相比于CEA均大幅度提高。 表5 高維下的實(shí)驗(yàn)結(jié)果對比 此外,繼續(xù)增加全局尋優(yōu)迭代次數(shù)至4000次,即CEA中Maxgen=4000、MSCEA中imax=4000,其余參數(shù)設(shè)置與3.3節(jié)和3.4.1節(jié)一致,實(shí)驗(yàn)結(jié)果見表6。從表6可以看出,CEA的尋優(yōu)精度雖然有所提高,但依舊未能得到f1~f7函數(shù)的最優(yōu)值。而MSCEA對除f2外的函數(shù)均能找到最優(yōu)值,對于f2,尋優(yōu)精度也相比于CEA提升了17個(gè)數(shù)量級左右。 表6 增加全局尋優(yōu)迭代次數(shù)后的實(shí)驗(yàn)結(jié)果對比 綜上,在30、50、100維條件下,隨著維數(shù)的增加,MSCEA整體上都能表現(xiàn)出較好的尋優(yōu)效果。MSCEA不僅尋優(yōu)精度高,而且魯棒性強(qiáng),大部分測試函數(shù)的尋優(yōu)標(biāo)準(zhǔn)差不隨著維數(shù)的增加而增加,說明MSCEA尋優(yōu)性能優(yōu)越,在處理高維優(yōu)化問題方面具有一定的競爭優(yōu)勢。 本文針對持續(xù)爆破算法易陷入局部最優(yōu)、尋優(yōu)精度較低等缺點(diǎn),提出一種基于主從結(jié)構(gòu)的階段尋優(yōu)策略、并帶有動(dòng)態(tài)爆破半徑和反向搜索變異的多策略改進(jìn)的持續(xù)爆破算法。通過進(jìn)行MSCEA與CEA、MSCEA-1在低維下的實(shí)驗(yàn)數(shù)據(jù)對比,說明主從結(jié)構(gòu)的階段尋優(yōu)策略能有效平衡算法的局部尋優(yōu)和全局尋優(yōu)能力,引入的反向變異搜索策略可以提高算法跳出局部最優(yōu)的能力。將MSCEA與鯨魚優(yōu)化算法、灰狼優(yōu)化算法、螢火蟲算法等多種優(yōu)化算法的近期研究成果進(jìn)行比較,表明MSCEA能有效避免早熟收斂,提高算法精度,在優(yōu)化問題上具有較強(qiáng)的競爭優(yōu)勢。通過高維下的尋優(yōu)性能測試,說明MSCEA尋優(yōu)精度高、尋優(yōu)性能穩(wěn)定,可以有效處理高維優(yōu)化問題。此外,針對部分函數(shù)的高維優(yōu)化問題,如何能通過更少的全局尋優(yōu)迭代次數(shù)達(dá)到和低維時(shí)相同的尋優(yōu)精度和收斂速度,以及如何將MSCEA應(yīng)用于實(shí)際優(yōu)化問題,是今后需要研究改進(jìn)的方向。2 改進(jìn)的持續(xù)爆破算法
2.1 持續(xù)爆破算法(CEA)存在的問題
2.2 基于主從結(jié)構(gòu)的階段尋優(yōu)策略
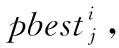
2.3 自適應(yīng)動(dòng)態(tài)爆破半徑
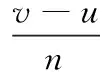
2.4 階段最優(yōu)解的反向搜索變異
2.5 每次階段尋優(yōu)初始炸點(diǎn)的位置更新策略
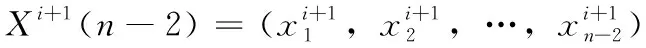
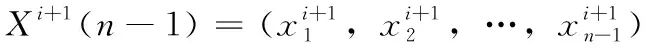
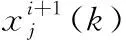
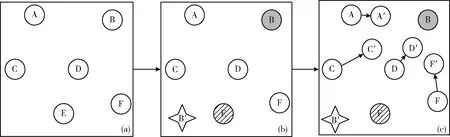
2.6 具體步驟如下
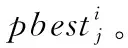
3 仿真實(shí)驗(yàn)與結(jié)果分析
3.1 仿真實(shí)驗(yàn)環(huán)境
3.2 測試函數(shù)

3.3 參數(shù)設(shè)置
3.4 實(shí)驗(yàn)結(jié)果及分析

3.5 高維下的性能測試
4 結(jié)束語

