多徑異步LSC-DS-CDMA信號偽碼估計

潘微宇，趙知勁,2

(1.杭州電子科技大學 通信工程學院，浙江 杭州 310018； 2.中國電子科技集團第36研究所 通信系統信息控制技術國家級重點實驗室，浙江 嘉興 314001)

0 引 言

直擴碼分多址(direct sequence code division multiple access，DS-CDMA)具有較強的抗干擾性和保密性，已被廣泛應用于軍事和民用通信中[1,2]。在非合作通信中，接收方要完成對截獲信號的解調，需要已知所用擴頻碼序列，因此，對DS-CDMA信號偽碼盲估計的研究具有重要意義。

目前對于長碼和短碼DS-CDMA信號偽碼估計的研究已有一些相應研究成果。文獻[3,4]分別利用無監督學習神經網絡和平行因子法完成了短碼DS-CDMA信號的偽碼估計。文獻[5]將長碼DS-CDMA信號構建為缺失數據的短碼DS-CDMA張量模型，并結合重疊窗法進行分段，利用嵌套迭代最小二乘投影插補法估計異步長碼DS-CDMA信號的偽碼。文獻[6]利用多天線接收信號，將長碼DS-CDMA信號構建為短碼DS-CDMA子張量，并使用變步長梯度下降法對子張量進行Tucker分解，得到各用戶的偽碼，估計性能比插補法更優。文獻[7]在文獻[6]的基礎上，使用交替最小二乘法對各子張量進行CP(canonical polyadic)分解得到各用戶偽碼，再利用庫搜索提高估計精度后，性能優于文獻[6]。對于短碼擴頻長碼加擾的LSC-DS-CDMA信號的偽碼估計，相關研究較少。文獻[7]的庫搜索無法用于LSC-DS-CDMA信號。文獻[8,9]在FastICA和m序列三階相關函數特性基礎上，分別結合矩陣填充法和分圓陪集理論估計LSC-DS-CDMA信號各用戶復合碼，再利用相關運算估計長碼和短碼，但矩陣填充法對噪聲敏感，三階相關特性在低信噪比下也難以獲得準確峰值。上述文獻均討論在理想信道下DS-CDMA信號偽碼的估計，而實際通信中大多都是多徑環境[10,11]。文獻[12]在文獻[5]模型的基礎上，使用正則最小交替二乘法估計多徑環境下長碼DS-CDMA信號偽碼，但其將多徑視作干擾，沒有解決多徑干擾對偽碼的影響，估計性能不佳。文獻[13]基于最大似然準則(maximum likelihood，ML)聯合估計單用戶長碼直擴信號偽碼和多徑信道，但不能直接應用于LSC-DS-CDMA信號的偽碼估計。

針對多徑環境下異步LSC-DS-CDMA信號偽碼估計問題，采用重疊窗對信號進行分段并構建子張量，利用動量梯度下降法和改進線性搜索步長算法對各個子張量進行Tucker張量分解估計復合碼，在提高復合碼估計準確率的同時，大大減少迭代次數，然后對含有多徑干擾的各用戶復合碼和多徑信道進行ML聯合估計，最后利用梅西算法和相關運算得到各用戶的長碼和短碼。

1 多徑異步LSC-DS-CDMA信號的TUCKER張量模型構建

設有U個用戶，用L根天線接收信號，且各用戶之間相互獨立，擴頻碼和長擾碼的周期已經估計得到，則第l根天線接收到的多徑LSC-DS-CDMA信號通過擴頻碼碼片速率采樣后基帶信號可以表示為

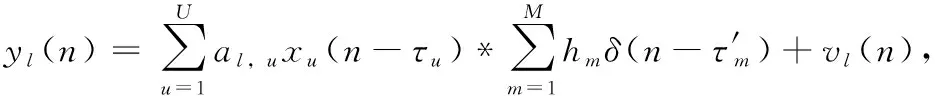
(1)

對于異步多徑LSC-DS-CDMA信號，各用戶主徑失步時間均不相同，若使用一倍擴頻碼周期進行分段，會導致不同用戶的每段信號a中包含的信息碼完整性不同而無法估計偽碼。因此本文按照2倍擴頻碼周期對接收信號進行重疊一半分段，對第w段信號，當w=jQ-1,j=1,2,…J時，使用長為(2Nb-1)的時間窗進行分段，對于其余段信號，利用長為2Nb的時間窗對信號進行分段，共得到W段信號。

則第l根天線接收信號的第w段信號可表示為

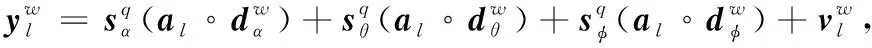
(2)

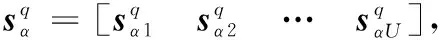
(3)

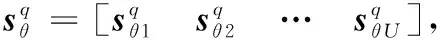
(4)

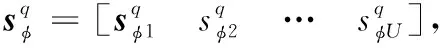
(5)

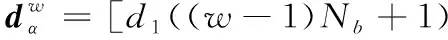
(6)

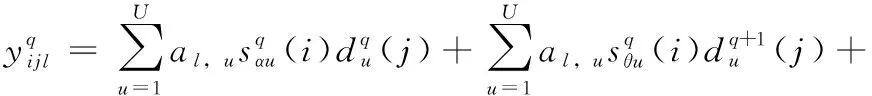
(7)

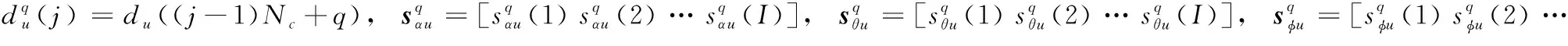
(8)

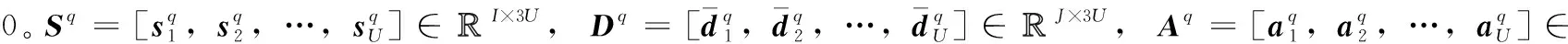
(9)

2 基于動量梯度下降法和改進線性搜索步長的復合碼片段估計

由于張量Tucker分解具有唯一性，對式(8)分解得到的因子矩陣分別對應各用戶的復合碼片段、信息碼片段和接收增益矩陣。定義張量最優化分解的目標函數為

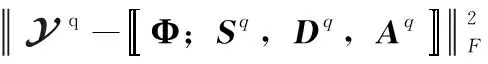
(10)

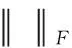
(11)

(12)

(13)

(14)

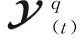
基于動量梯度下降的3個因子矩陣Aq，Sq，Dq的第k次更新公式為

Aq(k)=Aq(k-1)+μ(k)[λV(k-2)+(1-λ)G1(k-1)]
Dq(k)=Dq(k-1)+μ(k)[λV(k-2)+(1-λ)G2(k-1)]
Sq(k)=Sq(k-1)+μ(k)[λV(k-2)+(1-λ)G3(k-1)]

(15)

其中，μ(k) 為第k次迭代的實際步長，V(k)=λV(k-1)+(1-λ)Gi(k),i=1,2,3為動量項，λ為動量系數，引入動量項可提高收斂速度。

步長一般通過經典的線性搜索算法確定，但是該算法每次把步長初始化為一個固定值，這使得每次迭代的實際步長和初始步長的誤差均與下一次迭代的初始步長無關。由于這個誤差越大，會導致步長的搜索次數越多，從而影響收斂速度。因此，提出一種改進的線性搜索算法，利用上一次搜索的實際步長和初始步長的誤差值來確定下一次的初始步長，大大減少搜索次數，進一步提高算法的收斂速度。改進的線性搜索步長算法如下：

(1)步長初始化為μ0(k)=1；

(2)計算誤差函數f(Aq,Sq,Dq)，μ1=μ0(k)；

(3)當f(Aq+μ1G1,Dq+μ1G2,Sq+μ1G3)>f(Aq,Sq,Dq) 時，μ1=β1μ1，β1∈(0,1) 為固定參數；否則，循環結束，得到本次迭代的實際步長μ(k)=μ1。

(4)利用上次搜索的初始和實際步長，確定下次迭代的初始步長μ0(k+1)=(μ0(k)-β2μ(k))/(1+β2)，β2∈(0,1) 為固定參數。返回步驟(2)。

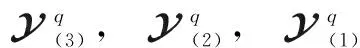
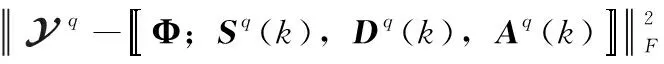
(16)

當f(k)-f(k-1)<β3(β3是一個極小的數)或者當迭代次數k達到最大值時，迭代結束。

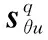
(17)

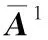
(18)

3 偽碼和多徑信道聯合估計

(19)

(20)

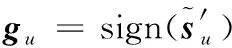
(21)

其中，0τ′m×1為τ′m×1維的零向量。由式(20)可見，h是待估計的多徑信道矩陣，Pu中包含了待估計的偽碼信息。

3.1 多徑信道估計

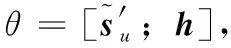
(22)

基于最大似然準則求解Pu和h，可等價為求下式的優化問題

(23)

首先僅考慮求解連續變量h。假設離散變量Pu已知，上式即為一個最小二乘問題，可求得

(24)

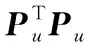
3.2 偽碼估計

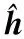
(25)

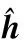
(26)

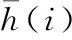
(27)

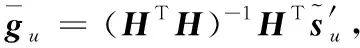
(28)

(29)

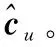
(30)

至此，U個用戶的長碼和短碼序列已經全部完成估計。

4 仿真分析

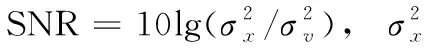
實驗1：用戶數與天線數對長短碼估計性能的影響

取萊斯因子K=5，短碼周期Nb=64，長擾碼周期Nc=255，用戶數U=2,3，天線數L=8,9，本文算法對長短碼估計的誤碼率曲線如圖1所示。

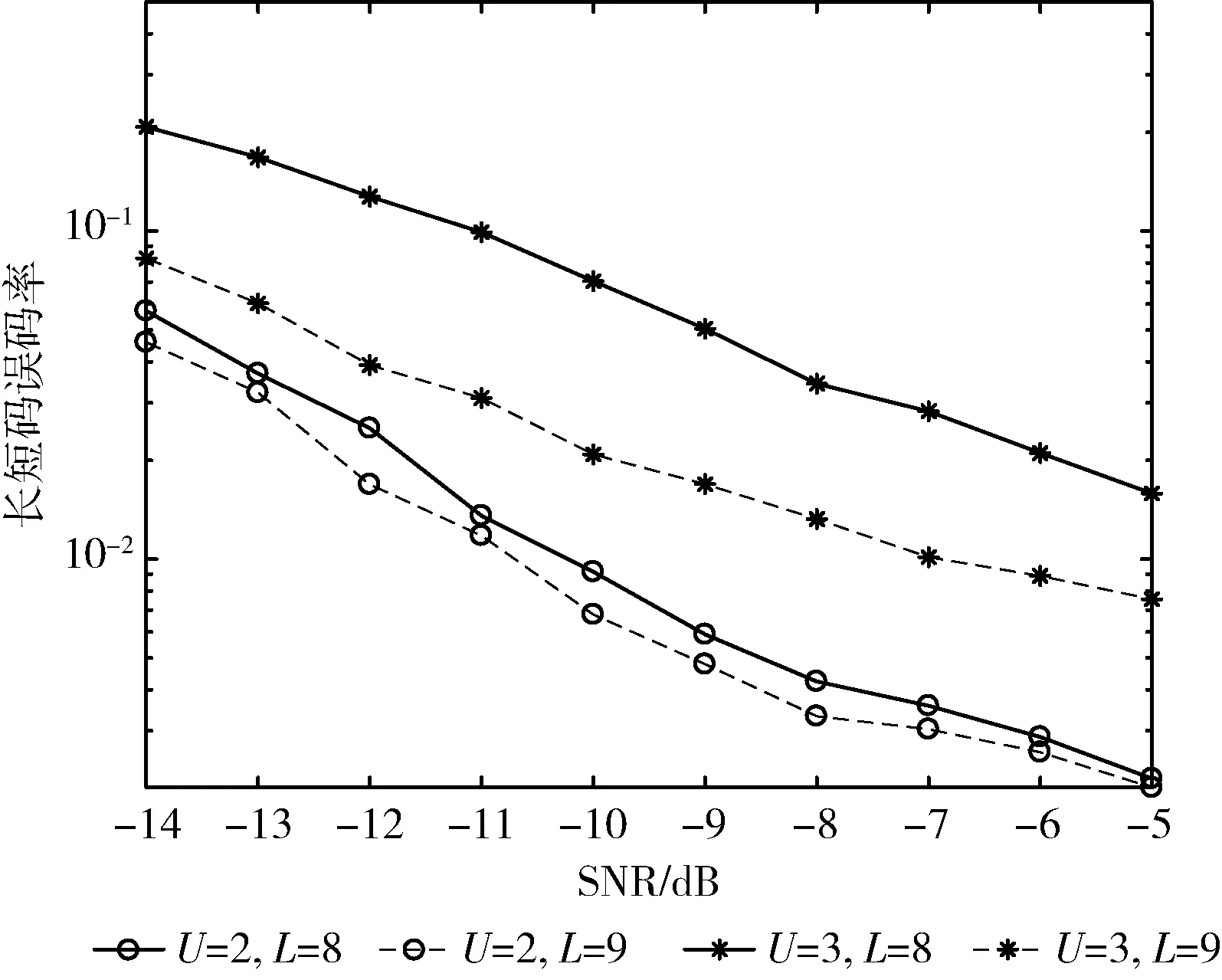
圖1 用戶數和天線數對估計性能的影響

由圖1可知，當接收天線數固定時，用戶數越多，長短碼的估計性能越差，這是由于用戶數越多，導致各用戶間的干擾也越大，從而影響估計性能；當用戶數固定時，天線數越多，長短碼估計性能越好，這是因為天線數越多，則接收到的可利用信號越多，估計誤差也就越小。當L<3U時無法使用HOSVD初始化張量分解的因子矩陣，因此在實驗中利用隨機生成的(3U-L)維矩陣和L維左奇異向量矩陣拼接構成的矩陣初始化因子矩陣，估計性能有明顯下降。

實驗2：短碼周期和長擾碼周期對長短碼估計性能的影響

取萊斯因子K=5，天線數L=9，用戶數U=3，當Nc=255，Nb=32和Nb=64以及Nc=511，Nb=32和Nb=64時，本文算法對長短碼估計的誤碼率曲線如圖2所示。

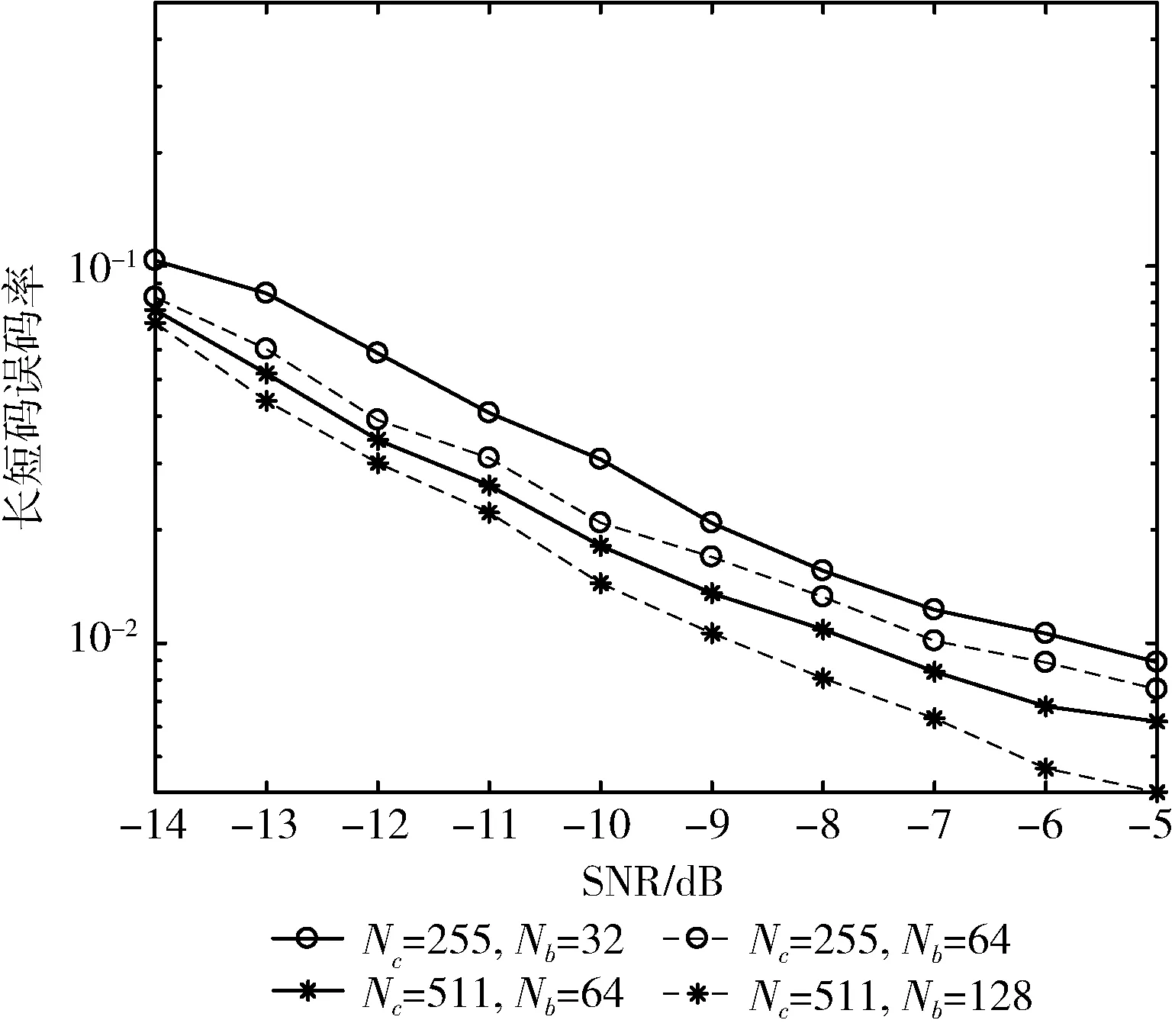
圖2 擴頻碼周期和長擾碼周期對估計性能的影響

由圖2可知，當長擾碼周期長度固定時，擴頻短碼周期越大，估計性能越好，這是因為分割的子張量越少，所需估計的偽碼片段就越少，產生的誤差也就越少，因此誤碼率就越小。當分割的子張量數目相同時，長擾碼周期長度越長，估計性能越好，這是由于長擾碼周期越長，梅西算法可處理的數據更多，對長擾碼的估計越準確，因此估計性能越好。

實驗3：ML聯合估計算法對復合碼估計性能的改善。

取萊斯因子K=1.25,5,10， 天線數L=9，用戶數U=3，短碼周期Nb=64，長擾碼周期Nc=255，本文算法對復合碼估計的誤碼率曲線如圖3所示。

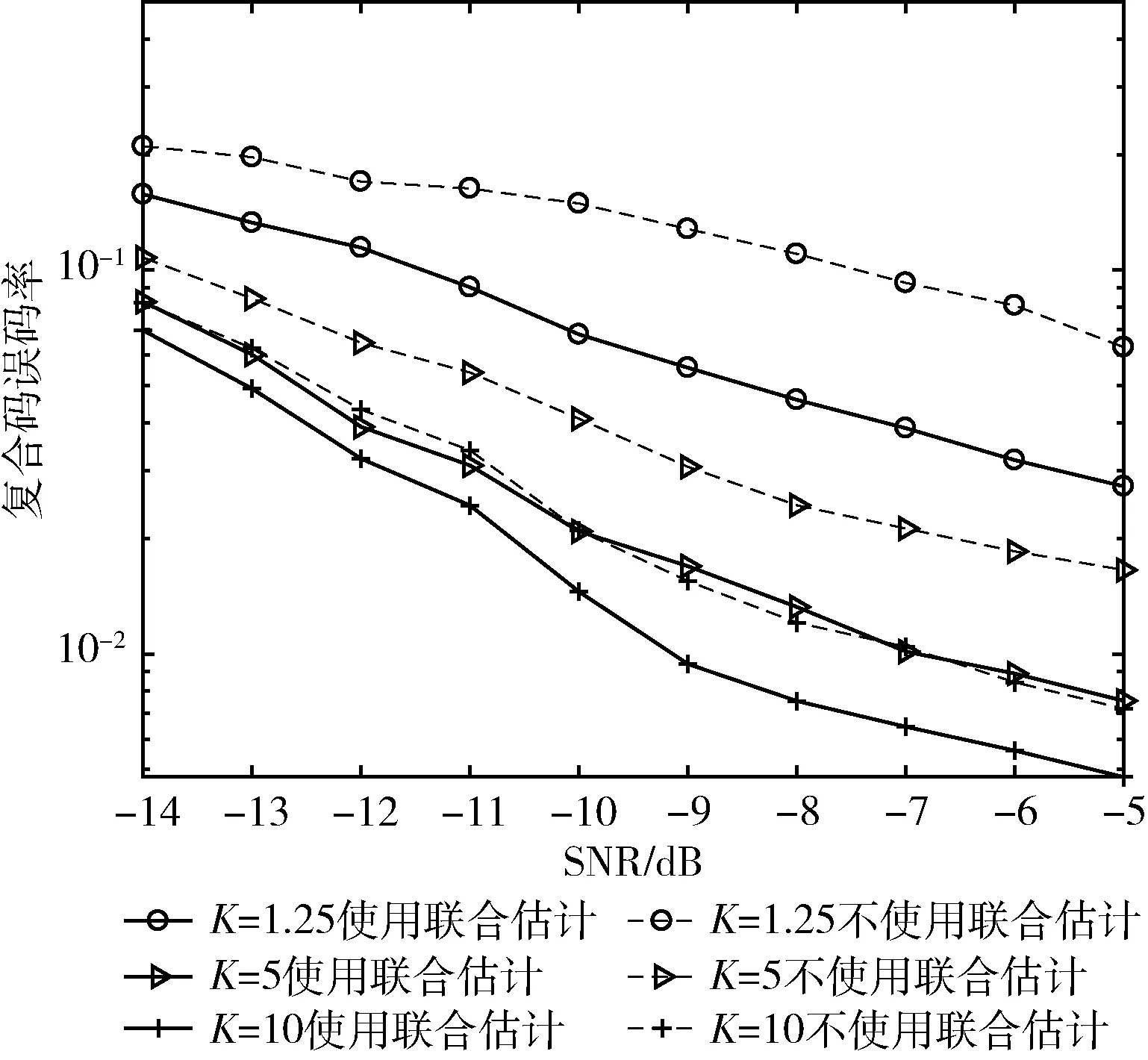
圖3 萊斯因子與聯合估計對復合碼估計性能的影響

由圖3可知，隨著萊斯因子逐漸增大，算法對復合碼的估計性能越好，這是由于萊斯因子越大，信號中主徑分量越強，其余徑分量越弱，多徑影響減弱，估計性能也就越好；當萊斯因子K分別為1.25、5和10時，使用ML聯合估計算法比不使用該算法的復合碼估計性能提升分別約5 dB、4 dB、3 dB，萊斯因子越大，ML聯合估計算法對復合碼的估計性能提升越小。

實驗4：算法性能對比

取萊斯因子K=5，天線數L=9，用戶數U=3，Nb=64，Nc=255，本文算法、文獻[6]、文獻[7]與文獻[12]的復合碼估計的誤碼率曲線如圖4(a)所示，迭代次數如圖4(b)所示。

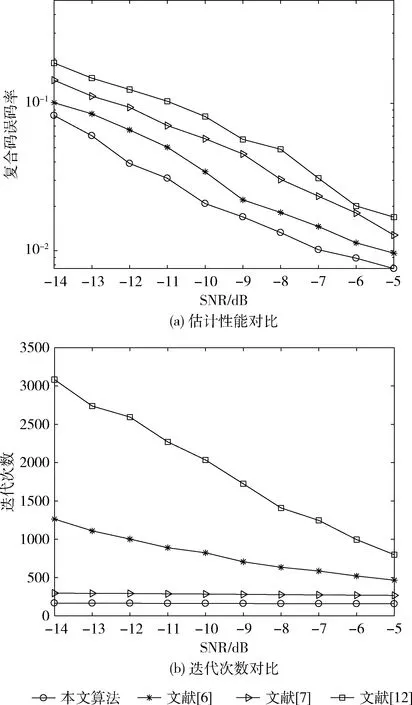
圖4 本文算法與對比算法的估計性能和迭代次數

由圖4(a)可知，本文所使用的算法估計性能最佳，文獻[6]算法次之，文獻[12]算法性能最差，這是因為本文算法和文獻[6]、文獻[7]均使用張量分解，避免了對數據的插補，估計性能均優于文獻[12]，本文使用動量梯度下降法，相比于文獻[6]的經典梯度算法，性能有所提升；文獻[7]的CP分解性能比Tucker分解的差，并且多項式庫搜索無法適用于本文所提的復合碼，在實驗中沒有使用庫搜索，因此性能不佳。由圖4(b)可知，本文算法迭代次數最少，文獻[7]算法迭代次數次之，文獻[12]算法迭代次數最多，且前兩種算法迭代次數幾乎與信噪比無關。這是因為本文算法改進了線性步長搜索算法，大大減少了迭代次數，文獻[12]由于插補法誤差較大，導致迭代次數增加。

5 結束語

針對多徑環境下的異步LSC-DS-CDMA信號的偽碼盲估計問題，本文先利用重疊窗分段信號并構建成Tucker張量模型，利用改進的線性搜索步長結合動量梯度下降法來估計因子矩陣，然后利用接收增益因子矩陣的互相關性和移位相乘分別解決排序和幅度模糊問題，使用ML準則對復合碼和多徑信道進行聯合估計。最后利用梅西算法和相關運算得到各個用戶的長擾碼和擴頻碼。仿真實驗結果表明，本文算法在估計性能和收斂速度上都優于現有算法。