基于流固耦合的降排截水法影響因素權重分析★

趙 誼，譚文超，楊雅鑠，張 宇，盧 斌，謝興華

（1.中國電建集團貴陽勘測設計研究院有限公司，貴州 貴陽 550081；2.河海大學水利水電學院，江蘇 南京 210024； 3.南京水利科學研究院，江蘇 南京 210029）

1 概述

為解決土地資源緊張，實現城市可持續發展等問題，地下空間的開發成為必然趨勢［1］。地下結構相較于地上結構，會受到浮力的影響，受力情況更為復雜，對于自重不能抵抗浮力的地下結構，會出現地下結構抗浮失穩的現象。地下結構存在抗浮失穩危險時，需要采取相應的抗浮措施進行抗浮。根據抗浮措施作用機理的不同，抗浮措施可分為主動抗浮措施和被動抗浮措施［2］。被動抗浮措施主要通過提高抗浮力來滿足抗浮穩定，如壓重抗浮、抗浮樁、抗浮錨桿等方法。主動抗浮措施主要通過降低水浮力來滿足抗浮穩定，如降排截水法。被動抗浮措施通常不夠經濟，而降排截水法抗浮效果較好，且經濟實用，故在實際工程中具有重要意義。

降排截水法（也稱泄水減壓法）是通過降水、排水、截水等處理措施直接降低地下結構所受到的浮力，它的原理是通過布置系統性的降排水設施，降低地下水位，進而減少地下結構所受的浮力，以此來達到抗浮穩定［3］。但降排水時需要注意，降水過多會導致地面沉降、墻體變形等問題［4］，因此在采取降水措施時，通常結合截水措施，如隔水帷幕，來減小由降水引起的沉降問題。此外，當基底附近存在弱透水層時，弱透水層可以和隔水帷幕一同將基坑與內部和外界水隔絕開來，可大大減小對坑外土體、建筑的影響，故降排截水法適用于基底附近存在弱透水層的工程。

關于降排截水法影響因素的分析已有許多學者進行研究，Zhou Nianqing等［5］發現降水引起的地面沉降、地基變形等問題，可通過設置地下連續墻有效控制，張堯［6］認為止水帷幕與泄水孔抽水量對水位降深的影響顯著，Feng Shilun等［7］研究了降排截水法中基坑的空間效應，劉洋［8］對泄水減壓法的主要影響因素進行了敏感性分析，Zeng Chaofeng等［9］發現時間效應和尺寸效應是影響基坑變形的兩個主要因素，常西陽［10］認為地下水滲流作用對基坑變形的影響較大。目前雖對降排截水法影響因素的分析較多，但對于各個影響因素的權重分析仍然較少，本文將針對降排截水法影響因素的權重進行分析。

2 數值模擬模型

2.1 模型與材料參數

模擬基坑深5 m，占地12 m×12 m，取基坑的1/4作為對稱模型計算，對稱模型尺寸為31 m×31 m×25 m（長×寬×高）。初始地下水水位設置與地面齊平，采用降排截水法施工時在基坑四周設置混凝土墻作為隔水帷幕，墻深入地下10 m，厚0.5 m。土層模擬三層，即砂土層中夾雜3 m厚的黏土層，模型土層及基坑結構如圖1所示。土體采用的本構模型為摩爾-庫侖模型，土層特性見表1。

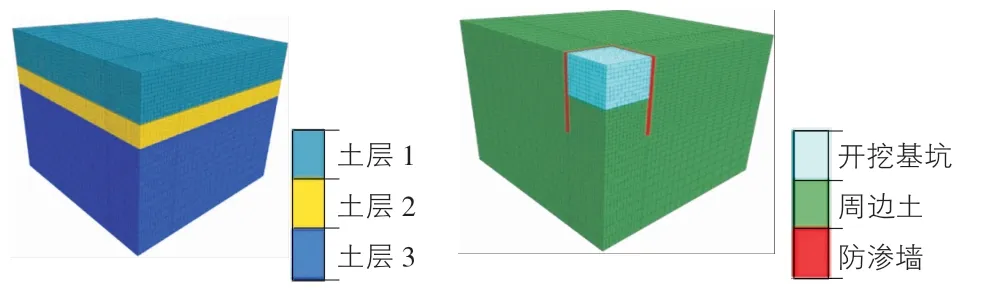
圖1 模型土層及基坑結構

表1 土層力學與滲流特性表

2.2 邊界條件與計算步驟

采用流固耦合分析方法進行數值模擬計算，模型的邊界條件主要分為力學邊界條件及流體邊界條件，力學邊界條件主要約束側面及底面法向方向位移，地表位移不受約束；流體邊界條件主要固定距基坑較遠處的x=31 m及y=31 m邊界的孔壓，其余邊界設為不透水邊界。

模擬計算的步驟主要為：構建土體與隔水帷幕的計算模型；設置自重應力場及流體條件，計算使得模型達到初始平衡；將初始地應力平衡狀態下的位移與速度歸零，設置隔水帷幕，并達到應力平衡；對基坑進行開挖與降水，并在基坑底部設置泄水孔，泄水孔處孔壓為0，進行流固耦合分析。初始孔壓、設置隔水帷幕后的孔壓云圖見圖2。

圖2 初始狀態與設置防滲墻后的孔隙水壓力圖

2.3 影響因素與工況

基于上述初始模型條件，對泄水孔數量、泄水孔間距、弱透水層厚度、弱透水層滲透系數及弱透水層相對位置5個影響因素進行分析，根據各影響因素調整各個工況采用的基礎數據，共模擬15組工況，各個工況的基本參數如表2所示。

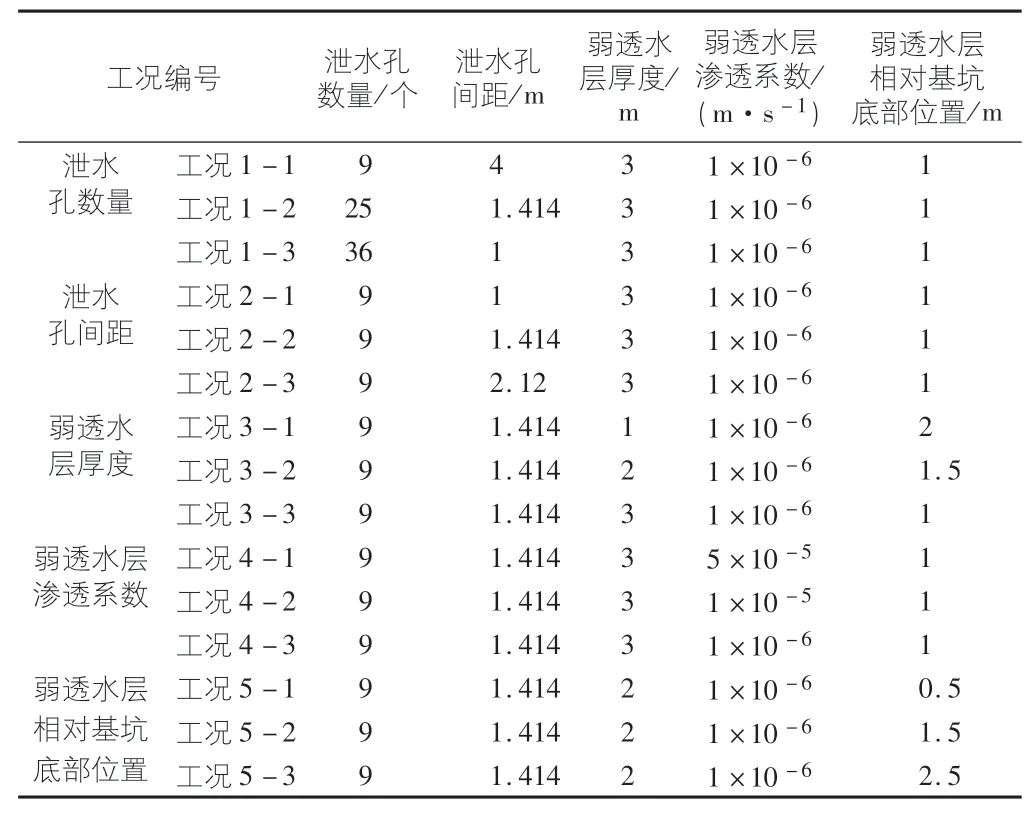
表2 數值模擬工況表

各工況下均通過設置監測點監測的沉降量來分析抗浮效果，以6 m×6 m基坑為坐標軸，監測點布置如圖3所示。

圖3 沉降監測點示意圖

3 模擬結果分析

以弱透水層厚度工況為例展示監測點沉降量和孔壓模擬結果，由圖4可見，當弱透水層越厚時，基底的孔隙水壓力明顯減小，各監測點處的沉降量越小。說明弱透水層起到了阻水作用，將基坑內的水與基坑外的水阻隔開來，對基坑內進行降水時，阻隔坑外水向坑內滲流。這也正是降排截水法的作用機理，通過基坑四周設置的防滲墻與基底的弱透水層組成一個隔水層，盡量減小基坑降水時對坑外地下水位的影響。

圖4 弱透水層厚度工況監測點沉降及孔壓結果

隨著弱透水層厚度的增加，各監測點的沉降差距減小，說明弱透水層的厚度對基坑底部的影響存在極值，當超過了這個極值之后，弱透水層的厚度對基坑底部的影響變化不大。對于一個工程，主要起到隔水作用的弱透水層厚度應該是一定的，當達到這個最佳厚度時則有較好的防滲效果，對于基底弱透水層厚度與最佳厚度相差較小時，可以考慮對基底土體進行處理來優化抗浮效果。

各工況基坑底部沉降量見圖5，其中工況5-1沉降量最大，為34.07 cm，工況1-3沉降量最小，為28.69 cm。為了對比各影響因素權重，采取基坑底部的平均沉降作為標準值進行分析。

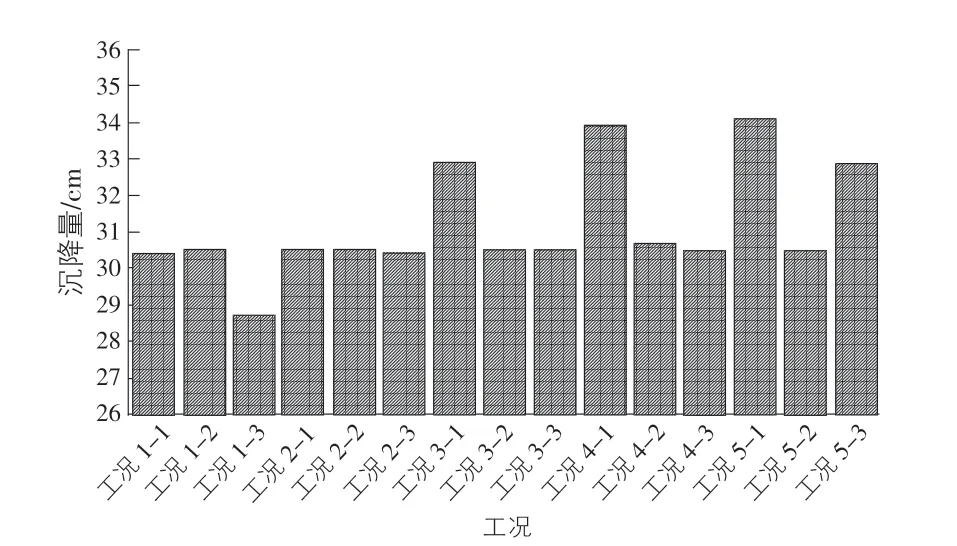
圖5 各工況基坑沉降量對比

4 影響因素權重分析

4.1 層次分析法計算

采用層次分析法，對泄水孔數量、間距、弱透水層厚度、滲透系數以及相對位置這5個影響因素進行權重分析。采用層次分析法來計算影響權重時，首先需要構建層次分析模型，層次結構模型有3層，分別為目標層、準則層以及對象層［11］。決策的目標即影響因素的權重，準則選為基坑的沉降量，對象即這5種影響因素。

通過回歸分析法，對5種影響因素和沉降量進行回歸分析，計算得出標準回歸系數見表3。

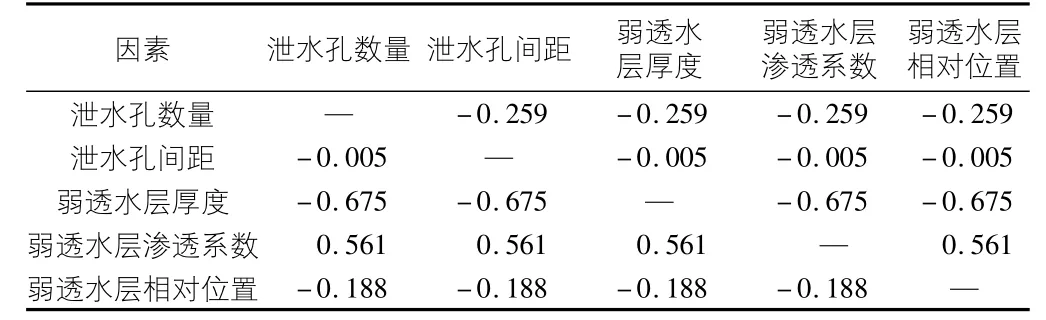
表3 標準回歸系數

根據標準回歸系數可計算得出每兩種影響因素的相對重要性比值，即兩種影響因素標準回歸系數比值的絕對值，通過任意兩種影響因素的相對重要性比值可構建層次分析法的判斷矩陣A［12］。

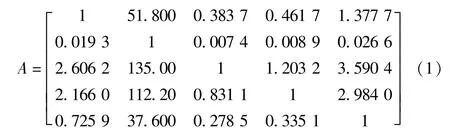
經計算得到判斷矩陣A的最大特征值為5，其對應的特征向量進行歸一化后為ω=（0.154，0.003，0.400，0.332，0.111）T。ω中的各元素即為各影響因素的權重值。

4.2 一致性檢驗

由于在計算分析模型的過程中，不可避免地會存在誤差，因此需要進行一致性檢驗。驗證判斷矩陣A的一致性時則需要計算檢驗系數CR，當CR＜0.1時，認為判斷矩陣A具有滿意的一致性，否則就需要對判斷矩陣進行適當修正并重新進行一致性檢驗。計算檢驗系數CR時引入了一致性指標CI這一概念：

其中，λmax為判斷矩陣A的最大特征值；n為判斷矩陣A的階數。當CI=0時，判斷矩陣具有完全的一致性；CI接近于0時，判斷矩陣有較滿意的一致性，CI越大，不一致越嚴重。為了衡量CI的大小，又引入了隨機一致性指標RI這一概念，隨機一致性指標RI與判斷矩陣A的階數有關，RI的取值見表4。

表4 隨機一致性指標

檢驗系數CR即為一致性指標CI與隨機一致性指標RI的比值，即：

通過計算得出判斷矩陣A的最大特征值為5，而其階數也是5，因此計算得出一致性指標CI=0，判斷矩陣A具有完全的一致性。

4.3 影響因素權重分析

泄水孔數量、泄水孔間距以及弱透水層厚度、滲透系數以及其相對位置的影響因素權重分別為0.154，0.003，0.400，0.332，0.111。其中弱透水層的厚度影響權重最大，弱透水層的滲透系數次之，泄水孔的間距影響權重最小。且弱透水層的厚度、滲透系數、相對位置三個影響因素的權重之和為0.843，故而可以認為弱透水層是影響降排截水法的最重要影響因素，其中尤以弱透水層的厚度與滲透系數為甚。

5 結論

1）降排截水法的隔水帷幕與基底附近的弱透水層形成隔水區，通過降低基坑內地下水來降低地下結構所受浮力，對基坑周圍建筑影響較小，且其具有良好的經濟性，因此在實際工程中具有重要意義。2）降排截水法中，弱透水層的厚度影響因素權重最大，為0.400；弱透水層滲透系數的影響因素權重次之，為0.332；泄水孔數量、泄水孔間距以及弱透水層相對位置的影響因素權重分別為0.154，0.003，0.111。3）弱透水層相關的影響因素，即弱透水層的厚度、滲透系數、相對位置3個影響因素，其權重之和為0.843，權重占比較大。故而可認為弱透水層是影響降排截水法的最重要影響因素，其中尤以弱透水層的厚度與滲透系數為甚。4）降排截水法通常用于基底附近存在弱透水層的工程，在實際工程中，可通過一些地基處理措施改善基底的透水性能，優化降排截水法的抗浮效果。